DOCSLIB.ORG

Approximate Inference Using MCMC

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Approximate Inference Using MCMC Approximate Inference using MCMC 9.520 Class 22 Ruslan Salakhutdinov BCS and CSAIL, MIT 1 Plan 1. Introduction/Notation. 2. Examples of successful Bayesian models. 3. Basic Sampling Algorithms. 4. Markov chains. 5. Markov chain Monte Carlo algorithms. 2 References/Acknowledgements • Chris Bishop’s book: Pattern Recognition and Machine Learning, chapter 11 (many figures are borrowed from this book). • David MacKay’s book: Information Theory, Inference, and Learning Algorithms, chapters 29-32. • Radford Neals’s technical report on Probabilistic Inference Using Markov Chain Monte Carlo Methods. • Zoubin Ghahramani’s ICML tutorial on Bayesian Machine Learning: http://www.gatsby.ucl.ac.uk/∼zoubin/ICML04-tutorial.html • Ian Murray’s tutorial on Sampling Methods: http://www.cs.toronto.edu/∼murray/teaching/ 3 Basic Notation P (x) probability of x P (x|θ) conditional probability of x given θ P (x, θ) joint probability of x and θ Bayes Rule: P (x|θ)P (θ) P (θ|x) = P (x) where P (x) = P (x, θ)dθ Marginalization Z I will use probability distribution and probability density interchangeably. It should be obvious from the context. 4 Inference Problem Given a dataset D = {x1, ..., xn}: Bayes Rule: P (D|θ) Likelihood function of θ P (D|θ)P (θ) P (θ|D)= P (θ) Prior probability of θ P (D) P (θ|D) Posterior distribution over θ Computing posterior distribution is known as the inference problem. But: P (D) = P (D,θ)dθ Z This integral can be very high-dimensional and difficult to compute. 5 Prediction P (D|θ) Likelihood function of θ P (D|θ)P (θ) P (θ|D)= P (D) P (θ) Prior probability of θ P (θ|D) Posterior distribution over θ Prediction: Given D, computing conditional probability of x∗ requires computing the following integral: P (x∗|D) = P (x∗|θ, D)P (θ|D)dθ Z E ∗ = P (θ|D)[P (x |θ, D)] which is sometimes called predictive distribution. Computing predictive distribution requires posterior P (θ|D). 6 Model Selection Compare model classes, e.g. M1 and M2. Need to compute posterior probabilities given D: P (D|M)P (M) P (M|D)= P (D) where P (D|M)= P (D|θ, M)P (θ, M)dθ Z is known as the marginal likelihood or evidence. 7 Computational Challenges • Computing marginal likelihoods often requires computing very high- dimensional integrals. • Computing posterior distributions (and hence predictive distributions) is often analytically intractable. • In this class, we will concentrate on Markov Chain Monte Carlo (MCMC) methods for performing approximate inference. • First, let us look at some specific examples: – Bayesian Probabilistic Matrix Factorization – Bayesian Neural Networks – Dirichlet Process Mixtures (last class) 8 Bayesian PMF User Features 1 2 3 4 5 6 7 ... 1 5 3 ? 1 ... V 2 3 ? 4 ? 3 2 ... 3 4 Movie 5 R ~ U Features 6 ~ 7 ... We have N users, M movies, and integer rating values from 1 to K. D×N D×M Let rij be the rating of user i for movie j, and U ∈ R , V ∈ R be latent user and movie feature matrices: R ≈ U ⊤V Goal: Predict missing ratings. 9 Bayesian PMF α α VU Probabilistic linear model with Gaussian observation noise. Likelihood: Θ Θ VU 2 ⊤ 2 p(rij|ui, vj, σ )= N (rij|ui vj, σ ) Gaussian Priors over parameters: Vj U i N p(U|µU , ΛU )= N (ui|µu, Σu), iY=1 Rij i=1,...,N M j=1,...,M p(V |µV , ΛV )= N (vi|µv, Σv). σ iY=1 Conjugate Gaussian-inverse-Wishart priors on the user and movie hyperparameters ΘU = {µu, Σu} and ΘV = {µv, Σv}. Hierarchical Prior. 10 Bayesian PMF ∗ Predictive distribution: Consider predicting a rating rij for user i and query movie j: ∗ ∗ p(r |R)= p(r |ui, vj)p(U, V, ΘU , ΘV |R)d{U, V }d{ΘU , ΘV } ij ZZ ij Posterior over parameters and hyperparameters | {z } Exact evaluation of this predictive distribution is analytically intractable. Posterior distribution p(U, V, ΘU , ΘV |R) is complicated and does not have a closed form expression. Need to approximate. 11 Bayesian Neural Nets X xn N Regression problem: Given a set of i.i.d observations = { }n=1 n N with corresponding targets D = {t }n=1. hidden units zM Likelihood: (1) N wMD (2) wKM n n 2 xD p(D|X, w)= N (t |y(x , w), β ) yK nY=1 inputs outputs The mean is given by the output y1 of the neural network: x1 M D x w 2 1 yk( , )= wkjσ wjixi z1 (2) w10 x0 Xj=0 Xi=0 where σ(x) is the sigmoid function. z0 Gaussian prior over the network parameters: p(w)= N (0, α2I). 12 Bayesian Neural Nets Likelihood: hidden units N zM n n 2 (1) p(D|X, w)= N (t |y(x , w), β ) wMD (2) wKM n=1 xD Y yK Gaussian prior over parameters: inputs outputs p(w)= N (0, α2I) y1 x1 Posterior is analytically intractable: z1 (2) w10 x0 w X w w X p(D| , )p( ) p( |D, )= w X w w z0 p(D| , )p( )d R Remark: Under certain conditions, Radford Neal (1994) showed, as the number of hidden units go to infinity, a Gaussian prior over parameters results in a Gaussian process prior for functions. 13 Undirected Models x is a binary random vector with xi ∈ {+1, −1}: 1 p(x)= exp θ x x + θ x . Z ij i j i i (i,jX)∈E iX∈V where Z is known as partition function: Z = exp θijxixj + θixi . Xx (i,jX)∈E iX∈V If x is 100-dimensional, need to sum over 2100 terms. The sum might decompose (e.g. junction tree). Otherwise we need to approximate. Remark: Compare to marginal likelihood. 14 Monte Carlo p(z) f(z) For most situations we will be interested in evaluating the expectation: E[f]= f(z)p(z)dz Z z p˜(z) We will use the following notation: p(z)= Z . We can evaluate p˜(z) pointwise, but cannot evaluate Z. 1 • Posterior distribution: P (θ|D)= P (D)P (D|θ)P (θ) 1 • Markov random fields: P (z)= Z exp(−E(z)) 15 Simple Monte Carlo General Idea: Draw independent samples {z1, ..., zn} from distribution p(z) to approximate expectation: N 1 E[f]= f(z)p(z)dz ≈ f(zn)= fˆ Z N nX=1 Note that E[f]= E[fˆ], so the estimator fˆhas correct mean (unbiased). The variance: 1 var[fˆ]= E (f − E[f])2 N Remark: The accuracy of the estimator does not depend on dimensionality of z. 16 Simple Monte Carlo In general: N 1 f(z)p(z)dz ≈ f(zn), zn ∼ p(z) Z N nX=1 Predictive distribution: P (x∗|D) = P (x∗|θ, D)P (θ|D)dθ Z N 1 ≈ P (x∗|θn, D), θn ∼ p(θ|D) N nX=1 Problem: It is hard to draw exact samples from p(z). 17 Basic Sampling Algorithm How to generate samples from simple non-uniform distributions assuming we can generate samples from uniform distribution. 1 h(y) y Define: h(y)= −∞ p(ˆy)dyˆ R p(y) Sample: z ∼ U[0, 1]. Then: y = h−1(z) is a sample from p(y). 0 y Problem: Computing cumulative h(y) is just as hard! 18 Rejection Sampling Sampling from target distribution p(z) =p ˜(z)/Zp is difficult. Suppose we have an easy-to-sample proposal distribution q(z), such that kq(z) ≥ p˜(z), ∀z. kq(z) Sample z0 from q(z). kq(z0) Sample u0 from Uniform[0, kq(z0)] p(z) u0 The pair (z0, u0) has uniform distribution e z0 z under the curve of kq(z). If u0 > p˜(z0), the sample is rejected. 19 Rejection Sampling Probability that a sample is accepted is: kq(z) kq(z0) p˜(z) p(accept) = q(z)dz Z kq(z) p(z) 1 u0 = p˜(z)dz e k Z z0 z The fraction of accepted samples depends on the ratio of the area under p˜(z) and kq(z). Hard to find appropriate q(z) with optimal k. Useful technique in one or two dimensions. Typically applied as a subroutine in more advanced algorithms. 20 Importance Sampling Suppose we have an easy-to-sample proposal distribution q(z), such that q(z) > 0 if p(z) > 0. p(z) q(z) f(z) E[f] = f(z)p(z)dz Z p(z) = f(z) q(z)dz Z q(z) 1 p(zn) ≈ f(zn), zn ∼ q(z) z N q(zn) Xn n n The quantities w = p(z )/q(zn) are known as importance weights. Unlike rejection sampling, all samples are retained. But wait: we cannot compute p(z), only p˜(z). 21 Importance Sampling Let our proposal be of the form q(z) =q ˜(z)/Zq: p(z) Z p˜(z) E[f] = f(z)p(z)dz = f(z) q(z)dz = q f(z) q(z)dz Z Z q(z) Zp Z q˜(z) Z 1 p˜(zn) Z 1 ≈ q f(zn)= q wnf(zn), zn ∼ q(z) Z N q˜(zn) Z N p Xn p Xn But we can use the same importance weights to approximate Zp: Zq Z 1 p˜(z) 1 p˜(zn) 1 p = p˜(z)dz = q(z)dz ≈ = wn Z Z q˜(z) N q˜(zn) N q q Z Z Xn Xn Hence: 1 wn E[f] ≈ f(zn) Consistentbutbiased. N wn Xn n P 22 Problems If our proposal distribution q(z) poorly matches our target distribution p(z) then: • Rejection Sampling: almost always rejects • Importance Sampling: has large, possibly infinite, variance (unreliable estimator).
Load more

Recommended publications
  • Practical Statistics for Particle Physics Lecture 1 AEPS2018, Quy Nhon, Vietnam
    Practical Statistics for Particle Physics Lecture 1 AEPS2018, Quy Nhon, Vietnam Roger Barlow The University of Huddersfield August 2018 Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 1 / 34 Lecture 1: The Basics 1 Probability What is it? Frequentist Probability Conditional Probability and Bayes' Theorem Bayesian Probability 2 Probability distributions and their properties Expectation Values Binomial, Poisson and Gaussian 3 Hypothesis testing Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 2 / 34 Question: What is Probability? Typical exam question Q1 Explain what is meant by the Probability PA of an event A [1] Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 3 / 34 Four possible answers PA is number obeying certain mathematical rules. PA is a property of A that determines how often A happens For N trials in which A occurs NA times, PA is the limit of NA=N for large N PA is my belief that A will happen, measurable by seeing what odds I will accept in a bet. Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 4 / 34 Mathematical Kolmogorov Axioms: For all A ⊂ S PA ≥ 0 PS = 1 P(A[B) = PA + PB if A \ B = ϕ and A; B ⊂ S From these simple axioms a complete and complicated structure can be − ≤ erected. E.g. show PA = 1 PA, and show PA 1.... But!!! This says nothing about what PA actually means. Kolmogorov had frequentist probability in mind, but these axioms apply to any definition. Roger Barlow ( Huddersfield) Statistics for Particle Physics August 2018 5 / 34 Classical or Real probability Evolved during the 18th-19th century Developed (Pascal, Laplace and others) to serve the gambling industry.
    [Show full text]
  • Markov Chain Monte Carlo Convergence Diagnostics: a Comparative Review
    Markov Chain Monte Carlo Convergence Diagnostics: A Comparative Review By Mary Kathryn Cowles and Bradley P. Carlin1 Abstract A critical issue for users of Markov Chain Monte Carlo (MCMC) methods in applications is how to determine when it is safe to stop sampling and use the samples to estimate characteristics of the distribu- tion of interest. Research into methods of computing theoretical convergence bounds holds promise for the future but currently has yielded relatively little that is of practical use in applied work. Consequently, most MCMC users address the convergence problem by applying diagnostic tools to the output produced by running their samplers. After giving a brief overview of the area, we provide an expository review of thirteen convergence diagnostics, describing the theoretical basis and practical implementation of each. We then compare their performance in two simple models and conclude that all the methods can fail to detect the sorts of convergence failure they were designed to identify. We thus recommend a combination of strategies aimed at evaluating and accelerating MCMC sampler convergence, including applying diagnostic procedures to a small number of parallel chains, monitoring autocorrelations and cross- correlations, and modifying parameterizations or sampling algorithms appropriately. We emphasize, however, that it is not possible to say with certainty that a finite sample from an MCMC algorithm is rep- resentative of an underlying stationary distribution. 1 Mary Kathryn Cowles is Assistant Professor of Biostatistics, Harvard School of Public Health, Boston, MA 02115. Bradley P. Carlin is Associate Professor, Division of Biostatistics, School of Public Health, University of Minnesota, Minneapolis, MN 55455.
    [Show full text]
  • Meta-Learning MCMC Proposals
    Meta-Learning MCMC Proposals Tongzhou Wang∗ Yi Wu Facebook AI Research University of California, Berkeley [email protected] [email protected] David A. Moorey Stuart J. Russell Google University of California, Berkeley [email protected] [email protected] Abstract Effective implementations of sampling-based probabilistic inference often require manually constructed, model-specific proposals. Inspired by recent progresses in meta-learning for training learning agents that can generalize to unseen environ- ments, we propose a meta-learning approach to building effective and generalizable MCMC proposals. We parametrize the proposal as a neural network to provide fast approximations to block Gibbs conditionals. The learned neural proposals generalize to occurrences of common structural motifs across different models, allowing for the construction of a library of learned inference primitives that can accelerate inference on unseen models with no model-specific training required. We explore several applications including open-universe Gaussian mixture models, in which our learned proposals outperform a hand-tuned sampler, and a real-world named entity recognition task, in which our sampler yields higher final F1 scores than classical single-site Gibbs sampling. 1 Introduction Model-based probabilistic inference is a highly successful paradigm for machine learning, with applications to tasks as diverse as movie recommendation [31], visual scene perception [17], music transcription [3], etc. People learn and plan using mental models, and indeed the entire enterprise of modern science can be viewed as constructing a sophisticated hierarchy of models of physical, mental, and social phenomena. Probabilistic programming provides a formal representation of models as sample-generating programs, promising the ability to explore a even richer range of models.
    [Show full text]
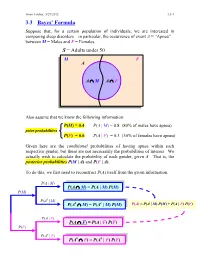
  • 3.3 Bayes' Formula
    Ismor Fischer, 5/29/2012 3.3-1 3.3 Bayes’ Formula Suppose that, for a certain population of individuals, we are interested in comparing sleep disorders – in particular, the occurrence of event A = “Apnea” – between M = Males and F = Females. S = Adults under 50 M F A A ∩ M A ∩ F Also assume that we know the following information: P(M) = 0.4 P(A | M) = 0.8 (80% of males have apnea) prior probabilities P(F) = 0.6 P(A | F) = 0.3 (30% of females have apnea) Given here are the conditional probabilities of having apnea within each respective gender, but these are not necessarily the probabilities of interest. We actually wish to calculate the probability of each gender, given A. That is, the posterior probabilities P(M | A) and P(F | A). To do this, we first need to reconstruct P(A) itself from the given information. P(A | M) P(A ∩ M) = P(A | M) P(M) P(M) P(Ac | M) c c P(A ∩ M) = P(A | M) P(M) P(A) = P(A | M) P(M) + P(A | F) P(F) P(A | F) P(A ∩ F) = P(A | F) P(F) P(F) P(Ac | F) c c P(A ∩ F) = P(A | F) P(F) Ismor Fischer, 5/29/2012 3.3-2 So, given A… P(M ∩ A) P(A | M) P(M) P(M | A) = P(A) = P(A | M) P(M) + P(A | F) P(F) (0.8)(0.4) 0.32 = (0.8)(0.4) + (0.3)(0.6) = 0.50 = 0.64 and posterior P(F ∩ A) P(A | F) P(F) P(F | A) = = probabilities P(A) P(A | M) P(M) + P(A | F) P(F) (0.3)(0.6) 0.18 = (0.8)(0.4) + (0.3)(0.6) = 0.50 = 0.36 S Thus, the additional information that a M F randomly selected individual has apnea (an A event with probability 50% – why?) increases the likelihood of being male from a prior probability of 40% to a posterior probability 0.32 0.18 of 64%, and likewise, decreases the likelihood of being female from a prior probability of 60% to a posterior probability of 36%.
    [Show full text]
  • Markov Chain Monte Carlo Edps 590BAY
    Markov Chain Monte Carlo Edps 590BAY Carolyn J. Anderson Department of Educational Psychology c Board of Trustees, University of Illinois Fall 2019 Overivew Bayesian computing Markov Chains Metropolis Example Practice Assessment Metropolis 2 Practice Overview ◮ Introduction to Bayesian computing. ◮ Markov Chain ◮ Metropolis algorithm for mean of normal given fixed variance. ◮ Revisit anorexia data. ◮ Practice problem with SAT data. ◮ Some tools for assessing convergence ◮ Metropolis algorithm for mean and variance of normal. ◮ Anorexia data. ◮ Practice problem. ◮ Summary Depending on the book that you select for this course, read either Gelman et al. pp 2751-291 or Kruschke Chapters pp 143–218. I am relying more on Gelman et al. C.J. Anderson (Illinois) MCMC Fall 2019 2.2/ 45 Overivew Bayesian computing Markov Chains Metropolis Example Practice Assessment Metropolis 2 Practice Introduction to Bayesian Computing ◮ Our major goal is to approximate the posterior distributions of unknown parameters and use them to estimate parameters. ◮ The analytic computations are fine for simple problems, ◮ Beta-binomial for bounded counts ◮ Normal-normal for continuous variables ◮ Gamma-Poisson for (unbounded) counts ◮ Dirichelt-Multinomial for multicategory variables (i.e., a categorical variable) ◮ Models in the exponential family with small number of parameters ◮ For large number of parameters and more complex models ◮ Algebra of analytic solution becomes overwhelming ◮ Grid takes too much time. ◮ Too difficult for most applications. C.J. Anderson (Illinois) MCMC Fall 2019 3.3/ 45 Overivew Bayesian computing Markov Chains Metropolis Example Practice Assessment Metropolis 2 Practice Steps in Modeling Recall that the steps in an analysis: 1. Choose model for data (i.e., p(y θ)) and model for parameters | (i.e., p(θ) and p(θ y)).
    [Show full text]
  • Numerical Physics with Probabilities: the Monte Carlo Method and Bayesian Statistics Part I for Assignment 2
    Numerical Physics with Probabilities: The Monte Carlo Method and Bayesian Statistics Part I for Assignment 2 Department of Physics, University of Surrey module: Energy, Entropy and Numerical Physics (PHY2063) 1 Numerical Physics part of Energy, Entropy and Numerical Physics This numerical physics course is part of the second-year Energy, Entropy and Numerical Physics mod- ule. It is online at the EENP module on SurreyLearn. See there for assignments, deadlines etc. The course is about numerically solving ODEs (ordinary differential equations) and PDEs (partial differential equations), and introducing the (large) part of numerical physics where probabilities are used. This assignment is on numerical physics of probabilities, and looks at the Monte Carlo (MC) method, and at the Bayesian statistics approach to data analysis. It covers MC and Bayesian statistics, in that order. MC is a widely used numerical technique, it is used, amongst other things, for modelling many random processes. MC is used in fields from statistical physics, to nuclear and particle physics. Bayesian statistics is a powerful data analysis method, and is used everywhere from particle physics to spam-email filters. Data analysis is fundamental to science. For example, analysis of the data from the Large Hadron Collider was required to extract a most probable value for the mass of the Higgs boson, together with an estimate of the region of masses where the scientists think the mass is. This region is typically expressed as a range of mass values where the they think the true mass lies with high (e.g., 95%) probability. Many of you will be analysing data (physics data, commercial data, etc) for your PTY or RY, or future careers1 .
    [Show full text]
  • The Bayesian Approach to Statistics
    THE BAYESIAN APPROACH TO STATISTICS ANTHONY O’HAGAN INTRODUCTION the true nature of scientific reasoning. The fi- nal section addresses various features of modern By far the most widely taught and used statisti- Bayesian methods that provide some explanation for the rapid increase in their adoption since the cal methods in practice are those of the frequen- 1980s. tist school. The ideas of frequentist inference, as set out in Chapter 5 of this book, rest on the frequency definition of probability (Chapter 2), BAYESIAN INFERENCE and were developed in the first half of the 20th century. This chapter concerns a radically differ- We first present the basic procedures of Bayesian ent approach to statistics, the Bayesian approach, inference. which depends instead on the subjective defini- tion of probability (Chapter 3). In some respects, Bayesian methods are older than frequentist ones, Bayes’s Theorem and the Nature of Learning having been the basis of very early statistical rea- Bayesian inference is a process of learning soning as far back as the 18th century. Bayesian from data. To give substance to this statement, statistics as it is now understood, however, dates we need to identify who is doing the learning and back to the 1950s, with subsequent development what they are learning about. in the second half of the 20th century. Over that time, the Bayesian approach has steadily gained Terms and Notation ground, and is now recognized as a legitimate al- ternative to the frequentist approach. The person doing the learning is an individual This chapter is organized into three sections.
    [Show full text]
  • Bayesian Phylogenetics and Markov Chain Monte Carlo Will Freyman
    IB200, Spring 2016 University of California, Berkeley Lecture 12: Bayesian phylogenetics and Markov chain Monte Carlo Will Freyman 1 Basic Probability Theory Probability is a quantitative measurement of the likelihood of an outcome of some random process. The probability of an event, like flipping a coin and getting heads is notated P (heads). The probability of getting tails is then 1 − P (heads) = P (tails). • The joint probability of event A and event B both occuring is written as P (A; B). The joint probability of mutually exclusive events, like flipping a coin once and getting heads and tails, is 0. • The probability of A occuring given that B has already occurred is written P (AjB), which is read \the probability of A given B". This is a conditional probability. • The marginal probability of A is P (A), which is calculated by summing or integrating the joint probability over B. In other words, P (A) = P (A; B) + P (A; not B). • Joint, conditional, and marginal probabilities can be combined with the expression P (A; B) = P (A)P (BjA) = P (B)P (AjB). • The above expression can be rearranged into Bayes' theorem: P (BjA)P (A) P (AjB) = P (B) Bayes' theorem is a straightforward and uncontroversial way to calculate an inverse conditional probability. • If P (AjB) = P (A) and P (BjA) = P (B) then A and B are independent. Then the joint probability is calculated P (A; B) = P (A)P (B). 2 Interpretations of Probability What exactly is a probability? Does it really exist? There are two major interpretations of probability: • Frequentists believe that the probability of an event is its relative frequency over time.
    [Show full text]
  • Paradoxes and Priors in Bayesian Regression
    Paradoxes and Priors in Bayesian Regression Dissertation Presented in Partial Fulfillment of the Requirements for the Degree Doctor of Philosophy in the Graduate School of The Ohio State University By Agniva Som, B. Stat., M. Stat. Graduate Program in Statistics The Ohio State University 2014 Dissertation Committee: Dr. Christopher M. Hans, Advisor Dr. Steven N. MacEachern, Co-advisor Dr. Mario Peruggia c Copyright by Agniva Som 2014 Abstract The linear model has been by far the most popular and most attractive choice of a statistical model over the past century, ubiquitous in both frequentist and Bayesian literature. The basic model has been gradually improved over the years to deal with stronger features in the data like multicollinearity, non-linear or functional data pat- terns, violation of underlying model assumptions etc. One valuable direction pursued in the enrichment of the linear model is the use of Bayesian methods, which blend information from the data likelihood and suitable prior distributions placed on the unknown model parameters to carry out inference. This dissertation studies the modeling implications of many common prior distri- butions in linear regression, including the popular g prior and its recent ameliorations. Formalization of desirable characteristics for model comparison and parameter esti- mation has led to the growth of appropriate mixtures of g priors that conform to the seven standard model selection criteria laid out by Bayarri et al. (2012). The existence of some of these properties (or lack thereof) is demonstrated by examining the behavior of the prior under suitable limits on the likelihood or on the prior itself.
    [Show full text]
  • The Markov Chain Monte Carlo Approach to Importance Sampling
    The Markov Chain Monte Carlo Approach to Importance Sampling in Stochastic Programming by Berk Ustun B.S., Operations Research, University of California, Berkeley (2009) B.A., Economics, University of California, Berkeley (2009) Submitted to the School of Engineering in partial fulfillment of the requirements for the degree of Master of Science in Computation for Design and Optimization at the MASSACHUSETTS INSTITUTE OF TECHNOLOGY September 2012 c Massachusetts Institute of Technology 2012. All rights reserved. Author.................................................................... School of Engineering August 10, 2012 Certified by . Mort Webster Assistant Professor of Engineering Systems Thesis Supervisor Certified by . Youssef Marzouk Class of 1942 Associate Professor of Aeronautics and Astronautics Thesis Reader Accepted by . Nicolas Hadjiconstantinou Associate Professor of Mechanical Engineering Director, Computation for Design and Optimization 2 The Markov Chain Monte Carlo Approach to Importance Sampling in Stochastic Programming by Berk Ustun Submitted to the School of Engineering on August 10, 2012, in partial fulfillment of the requirements for the degree of Master of Science in Computation for Design and Optimization Abstract Stochastic programming models are large-scale optimization problems that are used to fa- cilitate decision-making under uncertainty. Optimization algorithms for such problems need to evaluate the expected future costs of current decisions, often referred to as the recourse function. In practice, this calculation is computationally difficult as it involves the evaluation of a multidimensional integral whose integrand is an optimization problem. Accordingly, the recourse function is estimated using quadrature rules or Monte Carlo methods. Although Monte Carlo methods present numerous computational benefits over quadrature rules, they require a large number of samples to produce accurate results when they are embedded in an optimization algorithm.
    [Show full text]
  • A Widely Applicable Bayesian Information Criterion
    JournalofMachineLearningResearch14(2013)867-897 Submitted 8/12; Revised 2/13; Published 3/13 A Widely Applicable Bayesian Information Criterion Sumio Watanabe [email protected] Department of Computational Intelligence and Systems Science Tokyo Institute of Technology Mailbox G5-19, 4259 Nagatsuta, Midori-ku Yokohama, Japan 226-8502 Editor: Manfred Opper Abstract A statistical model or a learning machine is called regular if the map taking a parameter to a prob- ability distribution is one-to-one and if its Fisher information matrix is always positive definite. If otherwise, it is called singular. In regular statistical models, the Bayes free energy, which is defined by the minus logarithm of Bayes marginal likelihood, can be asymptotically approximated by the Schwarz Bayes information criterion (BIC), whereas in singular models such approximation does not hold. Recently, it was proved that the Bayes free energy of a singular model is asymptotically given by a generalized formula using a birational invariant, the real log canonical threshold (RLCT), instead of half the number of parameters in BIC. Theoretical values of RLCTs in several statistical models are now being discovered based on algebraic geometrical methodology. However, it has been difficult to estimate the Bayes free energy using only training samples, because an RLCT depends on an unknown true distribution. In the present paper, we define a widely applicable Bayesian information criterion (WBIC) by the average log likelihood function over the posterior distribution with the inverse temperature 1/logn, where n is the number of training samples. We mathematically prove that WBIC has the same asymptotic expansion as the Bayes free energy, even if a statistical model is singular for or unrealizable by a statistical model.
    [Show full text]
  • Markov Chain Monte Carlo (Mcmc) Methods
    MARKOV CHAIN MONTE CARLO (MCMC) METHODS 0These notes utilize a few sources: some insights are taken from Profs. Vardeman’s and Carriquiry’s lecture notes, some from a great book on Monte Carlo strategies in scientific computing by J.S. Liu. EE 527, Detection and Estimation Theory, # 4c 1 Markov Chains: Basic Theory Definition 1. A (discrete time/discrete state space) Markov chain (MC) is a sequence of random quantities {Xk}, each taking values in a (finite or) countable set X , with the property that P {Xn = xn | X1 = x1,...,Xn−1 = xn−1} = P {Xn = xn | Xn−1 = xn−1}. Definition 2. A Markov Chain is stationary if 0 P {Xn = x | Xn−1 = x } is independent of n. Without loss of generality, we will henceforth name the elements of X with the integers 1, 2, 3,... and call them “states.” Definition 3. With 4 pij = P {Xn = j | Xn−1 = i} the square matrix 4 P = {pij} EE 527, Detection and Estimation Theory, # 4c 2 is called the transition matrix for a stationary Markov Chain and the pij are called transition probabilities. Note that a transition matrix has nonnegative entries and its rows sum to 1. Such matrices are called stochastic matrices. More notation for a stationary MC: Define (k) 4 pij = P {Xn+k = j | Xn = i} and (k) 4 fij = P {Xn+k = j, Xn+k−1 6= j, . , Xn+1 6= j, | Xn = i}. These are respectively the probabilities of moving from i to j in k steps and first moving from i to j in k steps.
    [Show full text]