DOCSLIB.ORG

Condensation Fact Sheet

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Condensation Fact Sheet Condensation Fact Sheet METAL BUILDING MANUFACTURERS ASSOCIATION The Condensation Process In metal building systems, we are concerned with two different Condensation occurs when warmer moist air comes in contact areas or locations: visible condensation which occurs on with cold surfaces such as framing members, windows and surfaces below dew point temperatures; and concealed other accessories, or the colder region within the insulation condensation which occurs when moisture has passed into envelope (if moisture has penetrated the vapor retarder). Warm interior regions and then condenses on a surface that is below air, having the ability to contain more moisture than cold air, the dew point temperature. loses that ability when it comes in contact with cool or cold surfaces or regions. When that happens, excessive moisture Signs of visible surface condensation are water, frost or ice on in the air is released in the form of condensation. In metal windows, doors, frames, ceilings, walls, floor, insulation vapor buildings, there are two possible consequences of trapped retarders, skylights, cold water pipes and/or cooling ducts. To moisture in wall and roof systems: (1) corrosion of metal effectively control visible condensation, it is necessary to reduce components and (2) degradation of the thermal performance of the cold surface areas where condensation may occur. It is also insulation. important to minimize the air moisture content within a building by the use of properly designed ventilating systems. Dew Point and Relative Humidity Dew point is the temperature at which water vapor in any Signs of concealed condensation include damp spots, stains, static or moving air column will condense into water. In other mold and/or mildew on walls or ceilings, delamination of words, the air is saturated and can no longer hold the moisture laminated surfaces, bubbles or blisters in asphaltic surfaces, at this temperature. When the air temperature drops below peeling paint, and damp insulation. Concealed condensation is its dew point, excess moisture will be released in the form of the most difficult to deal with and can be the most damaging. condensation. Condensation problems are most likely to occur This type of condensation may be controlled in metal buildings in climates where temperatures frequently dip to 35°F or colder by the proper use of vapor retarders and by minimizing moisture over an extended period of time. content within the building by proper ventilation. Additional condensation control can be accomplished by venting the Relative humidity is a percentage measurement of the amount cavities of the walls and roof. of water vapor present in the air in relation to the amount it is capable of holding at that temperature. For example, 50% Vapor Retarders relative humidity indicates the air is carrying one-half of the A vapor retarder is used to inhibit the passage of warmer maximum amount of moisture that it is capable of containing at moist air into the inner regions of the roof or wall system. The the given temperature. There is a relationship between the dew proper selection and installation of the vapor retarder can help point and relative humidity. A high relative humidity means that control condensation problems in a building. Vapor retarders the dew point is near the current air temperature. Therefore, a are rated by the amount of moisture that can pass through relative humidity of 100% indicates that the dew point is equal them. The lower this rating, called a perm rating, the less vapor to the current temperature. This relationship between dew point transmission will occur and the more effective the vapor retarder and relative humidity is given in Table C-1. will be. Water vapor transmission rates (perms) are determined using ASTM E 96, Standard Test Methods for Water Vapor Visible and Concealed Condensation Transmission of Materials (ASTM, 2005). Two things must be present for condensation to occur: warm moist air, and cool surface temperatures below the dew Types of Vapor Retarders point. The proper control of these two factors can minimize There are various types of vapor retarders available, such as: condensation. 1. Structural membranes, including rigid steel sheets or other Dew Point Temperature (oF)1 Relative Design Dry Bulb (Interior) Temperature Humidity 32oF 35oF 40oF 45oF 50oF 55oF 60oF 65oF 70oF 75oF 80oF 85oF 90oF 95oF 100oF 100% 32 35 40 45 50 55 60 65 70 75 80 85 90 95 100 90% 30 33 37 42 47 52 57 62 67 72 77 82 87 92 97 80% 27 30 34 39 44 49 54 58 64 68 73 78 83 88 93 70% 24 27 31 36 40 45 50 55 60 64 69 74 79 84 88 60% 20 24 28 32 36 41 46 51 55 60 65 69 74 79 83 50% 16 20 24 28 33 36 41 46 50 55 60 64 69 73 78 40% 12 15 18 23 27 31 35 40 45 49 53 58 62 67 71 30% 8 10 14 16 21 25 29 33 37 42 46 50 54 59 62 20% 6 7 8 9 13 16 20 24 28 31 35 40 43 48 52 10% 4 4 5 5 6 8 9 10 13 17 20 24 27 30 34 1 Chart adapted from ASHRAE Psychometric Chart, 2005 ASHRAE Handbook of Fundamentals Table C-1: Dew Point Temperature (oF)1 verses Relative Humidity impermeable materials. The list below is not exhaustive, nor is it Besides the most popular facings, the industry provides special an effort to limit the designer, but these membranes may include facings that have high impact resistance for gymnasiums, facings the following in roof and/or wall construction: for high UV applications and black colored facings for structures a. Steel formed panels, properly sealed on edges and where ceilings are not used. ends. b. Steel, zinc alloy, copper or aluminum sheets with caulked Sealing Vapor Retarders and formed standing seam edges and ends. Careful attention must be paid to the insulation seams at side c. Vinyl siding applied to suitable structural substrate or and end-laps to maintain the integrity of the vapor retarder. sheathing. Some common methods used to seal the seams include rolling d. Tilt-up concrete panels, suitably sealed at end and side and stapling the side-laps, peel and stick tabs at side-laps, and laps, with a painted exterior. sometimes insulation tape. The use of insulation tape alone to e. Vinyl, metalized plastic and similar overlays on rigid seal the seams may not be advisable. Job site conditions such as board insulation. humidity, dirt, and access to the underside of the insulation can f. Foam insulated metal panels, caulked and sealed at ends make this difficult. Where used, tape should be at least the same and side laps. quality as the vapor retarder, and the tape should be approved by g. Bituminous spray or trowel-on coating on concrete or the insulation supplier for the particular product. In the case of a masonry. membrane type retarder, any punctures or tears in the material should be repaired using the self-adhesive repair tape supplied 2. Flexible membranes, such as foils, coated papers, or plastic with the insulation. More information and downloadable literature films. Usually, these membranes are rated by “perm” of 1.0 or can be found on the NAIMA website via http://www.naima.org, less, per ASTM E 96, Standard Test Methods for Water Vapor or visit National Insulation Association (NIA) at Transmission of Materials (ASTM, 2005). The most common http://www.insulation.org. applications for metal buildings are membrane retarders laminated to fiber glass blanket insulation. Plain white vinyl with a Because there is a growing trend to add insulation to existing perm rating of 1.0 is not an effective vapor retarder, especially in metal buildings, a proper vapor retarder is of critical concern. buildings with a high relative humidity. One of the most common methods is to add an additional layer of insulation to the bottom flange of the purlin system. This can 3. Coating membranes, which includes paints, trowel-on create an air space where moisture laden air can accumulate bituminous coatings, epoxy and urethane foams. if the integrity of the new vapor retarder closest to the warm insulating surface of the building has not been maintained. It Laminated facings for fiber glass batts serve several purposes is important that an intact vapor retarder is not left within the other than appearance. They prevent the blanket from sagging. insulation mass. They prevent most water vapor from penetrating the fiber glass batt. They provide resistance to impact and provide reflectivity Ventilation and emissivity benefits. Most facings have three parts: All metal buildings require some level of ventilation, and more often this ventilation is becoming the responsibility of the 1. A base made up of natural or white kraft paper or metal building contractor. A lack of ventilation can create an aluminum foil. uncomfortable working condition through elevated heat levels, 2. A fiber glass scrim netting is provided for reinforcing and excessive humidity, and stale air. It can also contribute to sag prevention. condensation problems. Ventilation can best be represented 3. An exterior film made up of polypropylene, vinyl, metalized by the number of times per hour the building air is replaced polyester, or aluminum foil is applied on top. with outside air. This is referred to as air changes per hour. The number of air changes required per hour widely varies per Table C-2 lists some of the most popular types of facings and application. shows their water vapor transmission rates (perm ratings). The North American Insulation Manufacturers Association (NAIMA) The following example illustrates a calculation for ventilation recommends that metal building insulation be faced with a vapor requirements: retarder having a permeance of not greater than 0.10 perms.
Load more

Recommended publications
  • How to Read a METAR
    How to read a METAR A METAR will look something like this: PHNY 202124Z AUTO 27009KT 1 1/4SM BR BKN016 BKN038 22/21 A3018 RMK AO2 Let’s decipher what each bit of the METAR means. PHNY The first part of the METAR is the airport identifier for the facility which produced the METAR. In this case, this is Lanai Airport in Hawaii. 202124Z Next comes the time and date of issue. The first two digits correspond to the date of the month, and the last 4 digits correspond to the time of issue (in Zulu time). In the example, the METAR was issued on the 20th of the month at 21:24 Zulu time. AUTO This part indicates that the METAR was generated automatically. 27009KT Next comes the wind information. The first 3 digits represent the heading from which the wind is blowing, and the next digits indicate speed in knots. In this case, the wind is coming from a heading of 270 relative to magnetic north, and the speed is 9 knots. Some other wind-related notation you might see: • 27009G15KT – the G indicates gusting. In this case, the wind comes from 270 at 9 knots, and gusts to 15 knots. • VRB09KT – the VRB indicates the wind direction is variable; the wind speed is 9 knots. 1 1/4SM This section of the METAR indicates visibility in statute miles. In this case, visibility is 1 ¼ statute miles. Note that the range is typically limited to 10 statute miles, so a report with 10 statute mile visibility could well indicate a situation with more than 10 statute miles of visibility.
    [Show full text]
  • Chapter 5 Measures of Humidity Phases of Water
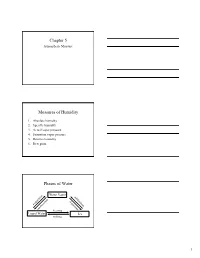
    Chapter 5 Atmospheric Moisture Measures of Humidity 1. Absolute humidity 2. Specific humidity 3. Actual vapor pressure 4. Saturation vapor pressure 5. Relative humidity 6. Dew point Phases of Water Water Vapor n o su ti b ra li o n m p io d a a at ep t v s o io e en s n d it n io o n c freezing Liquid Water Ice melting 1 Coexistence of Water & Vapor • Even below the boiling point, some water molecules leave the liquid (evaporation). • Similarly, some water molecules from the air enter the liquid (condense). • The behavior happens over ice too (sublimation and condensation). Saturation • If we cap the air over the water, then more and more water molecules will enter the air until saturation is reached. • At saturation there is a balance between the number of water molecules leaving the liquid and entering it. • Saturation can occur over ice too. Hydrologic Cycle 2 Air Parcel • Enclose a volume of air in an imaginary thin elastic container, which we will call an air parcel. • It contains oxygen, nitrogen, water vapor, and other molecules in the air. 1. Absolute Humidity Mass of water vapor Absolute humidity = Volume of air The absolute humidity changes with the volume of the parcel, which can change with temperature or pressure. 2. Specific Humidity Mass of water vapor Specific humidity = Total mass of air The specific humidity does not change with parcel volume. 3 Specific Humidity vs. Latitude • The highest specific humidities are observed in the tropics and the lowest values in the polar regions.
    [Show full text]
  • Role of the Dew Water on the Ground Surface in HONO Distribution: a Case Measurement in Melpitz
    Atmos. Chem. Phys., 20, 13069–13089, 2020 https://doi.org/10.5194/acp-20-13069-2020 © Author(s) 2020. This work is distributed under the Creative Commons Attribution 4.0 License. Role of the dew water on the ground surface in HONO distribution: a case measurement in Melpitz Yangang Ren1, Bastian Stieger2, Gerald Spindler2, Benoit Grosselin1, Abdelwahid Mellouki1, Thomas Tuch2, Alfred Wiedensohler2, and Hartmut Herrmann2 1Institut de Combustion, Aérothermique, Réactivité et Environnement (ICARE), CNRS (UPR 3021), Observatoire des Sciences de l’Univers en région Centre (OSUC), 1C Avenue de la Recherche Scientifique, 45071 Orléans CEDEX 2, France 2Leibniz Institute for Tropospheric Research (TROPOS), Permoserstraße 15, 04318 Leipzig, Germany Correspondence: Abdelwahid Mellouki ([email protected]) and Hartmut Herrmann ([email protected]) Received: 25 November 2019 – Discussion started: 30 January 2020 Revised: 27 August 2020 – Accepted: 13 September 2020 – Published: 9 November 2020 Abstract. To characterize the role of dew water for the eas that provide a large amount of ground surface based on ground surface HONO distribution, nitrous acid (HONO) the OH production rate calculation. measurements with a Monitor for AeRosols and Gases in am- bient Air (MARGA) and a LOng Path Absorption Photome- ter (LOPAP) instrument were performed at the Leibniz In- 1 Introduction stitute for Tropospheric Research (TROPOS) research site in Melpitz, Germany, from 19 to 29 April 2018. The dew water Nitrous acid (HONO) is important in atmospheric chemistry was also collected and analyzed from 8 to 14 May 2019 using as its photolysis (Reaction R1) is an important source of OH a glass sampler. The high time resolution of HONO measure- radicals.
    [Show full text]
  • Insar Water Vapor Data Assimilation Into Mesoscale Model
    This article has been accepted for inclusion in a future issue of this journal. Content is final as presented, with the exception of pagination. IEEE JOURNAL OF SELECTED TOPICS IN APPLIED EARTH OBSERVATIONS AND REMOTE SENSING 1 InSAR Water Vapor Data Assimilation into Mesoscale Model MM5: Technique and Pilot Study Emanuela Pichelli, Rossella Ferretti, Domenico Cimini, Giulia Panegrossi, Daniele Perissin, Nazzareno Pierdicca, Senior Member, IEEE, Fabio Rocca, and Bjorn Rommen Abstract—In this study, a technique developed to retrieve inte- an extremely important element of the atmosphere because its grated water vapor from interferometric synthetic aperture radar distribution is related to clouds, precipitation formation, and it (InSAR) data is described, and a three-dimensional variational represents a large proportion of the energy budget in the atmo- assimilation experiment of the retrieved precipitable water vapor into the mesoscale weather prediction model MM5 is carried out. sphere. Its representation inside numerical weather prediction The InSAR measurements were available in the framework of the (NWP) models is critical to improve the weather forecast. It is European Space Agency (ESA) project for the “Mitigation of elec- also very challenging because water vapor is involved in pro- tromagnetic transmission errors induced by atmospheric water cesses over a wide range of spatial and temporal scales. An vapor effects” (METAWAVE), whose goal was to analyze and pos- improvement in atmospheric water vapor monitoring that can sibly predict the phase delay induced by atmospheric water vapor on the spaceborne radar signal. The impact of the assimilation on be assimilated in NWP models would improve the forecast the model forecast is investigated in terms of temperature, water accuracy of precipitation and severe weather [1], [3].
    [Show full text]
  • Electricity Demand Reduction in Sydney and Darwin with Local Climate Mitigation
    P. Rajagopalan and M.M Andamon (eds.), Engaging Architectural Science: Meeting the Challenges of Higher Density: 52nd 285 International Conference of the Architectural Science Association 2018, pp.285–293. ©2018, The Architectural Science Association and RMIT University, Australia. Electricity demand reduction in Sydney and Darwin with local climate mitigation Riccardo Paolini UNSW Built Environment, UNSW Sydney, Australia [email protected] Shamila Haddad UNSW Built Environment, UNSW Sydney, Australia [email protected] Afroditi Synnefa UNSW Built Environment, UNSW Sydney, Australia [email protected] Samira Garshasbi UNSW Built Environment, UNSW Sydney, Australia [email protected] Mattheos Santamouris UNSW Built Environment, UNSW Sydney, Australia [email protected] Abstract: Urban overheating in synergy with global climate change will be enhanced by the increasing population density and increased land use in Australian Capital Cities, boosting the total and peak electricity demand. Here we assess the relation between ambient conditions and electricity demand in Sydney and Darwin and the impact of local climate mitigation strategies including greenery, cool materials, water and their combined use at precinct scale. By means of a genetic algorithm, we produced two site-specific surrogate models, for New South Wales and Darwin CBD, to compute the electricity demand as a function of air temperature, humidity and incoming solar radiation. For Western Sydney, the total electricity savings computed under the different mitigation scenarios range between 0.52 and 0.91 TWh for the summer of 2016/2017, namely 4.5 % of the total, with the most relevant saving concerning the peak demand, equal to 9 % with cool materials and water sprinkling.
    [Show full text]
  • Guide to Understanding Condensation
    Guide to Understanding Condensation The complete Andersen® Owner-To-Owner™ limited warranty is available at: www.andersenwindows.com. “Andersen” is a registered trademark of Andersen Corporation. All other marks where denoted are marks of Andersen Corporation. © 2007 Andersen Corporation. All rights reserved. 7/07 INTRODUCTION 2 The moisture that suddenly appears in cold weather on the interior We have created this brochure to answer questions you may have or exterior of window and patio door glass can block the view, drip about condensation, indoor humidity and exterior condensation. on the floor or freeze on the glass. It can be an annoying problem. We’ll start with the basics and offer solutions and alternatives While it may seem natural to blame the windows or doors, interior along the way. condensation is really an indication of excess humidity in the home. Exterior condensation, on the other hand, is a form of dew — the Should you run into problems or situations not covered in the glass simply provides a surface on which the moisture can condense. following pages, please contact your Andersen retailer. The important thing to realize is that if excessive humidity is Visit the Andersen website: www.andersenwindows.com causing window condensation, it may also be causing problems elsewhere in your home. Here are some other signs of excess The Andersen customer service toll-free number: 1-888-888-7020. humidity: • A “damp feeling” in the home. • Staining or discoloration of interior surfaces. • Mold or mildew on surfaces or a “musty smell.” • Warped wooden surfaces. • Cracking, peeling or blistering interior or exterior paint.
    [Show full text]
  • Chapter 3 Equations of State
    Chapter 3 Equations of State The simplest way to derive the Helmholtz function of a fluid is to directly integrate the equation of state with respect to volume (Sadus, 1992a, 1994). An equation of state can be applied to either vapour-liquid or supercritical phenomena without any conceptual difficulties. Therefore, in addition to liquid-liquid and vapour -liquid properties, it is also possible to determine transitions between these phenomena from the same inputs. All of the physical properties of the fluid except ideal gas are also simultaneously calculated. Many equations of state have been proposed in the literature with either an empirical, semi- empirical or theoretical basis. Comprehensive reviews can be found in the works of Martin (1979), Gubbins (1983), Anderko (1990), Sandler (1994), Economou and Donohue (1996), Wei and Sadus (2000) and Sengers et al. (2000). The van der Waals equation of state (1873) was the first equation to predict vapour-liquid coexistence. Later, the Redlich-Kwong equation of state (Redlich and Kwong, 1949) improved the accuracy of the van der Waals equation by proposing a temperature dependence for the attractive term. Soave (1972) and Peng and Robinson (1976) proposed additional modifications of the Redlich-Kwong equation to more accurately predict the vapour pressure, liquid density, and equilibria ratios. Guggenheim (1965) and Carnahan and Starling (1969) modified the repulsive term of van der Waals equation of state and obtained more accurate expressions for hard sphere systems. Christoforakos and Franck (1986) modified both the attractive and repulsive terms of van der Waals equation of state. Boublik (1981) extended the Carnahan-Starling hard sphere term to obtain an accurate equation for hard convex geometries.
    [Show full text]
  • Chapter 3 Bose-Einstein Condensation of an Ideal
    Chapter 3 Bose-Einstein Condensation of An Ideal Gas An ideal gas consisting of non-interacting Bose particles is a ¯ctitious system since every realistic Bose gas shows some level of particle-particle interaction. Nevertheless, such a mathematical model provides the simplest example for the realization of Bose-Einstein condensation. This simple model, ¯rst studied by A. Einstein [1], correctly describes important basic properties of actual non-ideal (interacting) Bose gas. In particular, such basic concepts as BEC critical temperature Tc (or critical particle density nc), condensate fraction N0=N and the dimensionality issue will be obtained. 3.1 The ideal Bose gas in the canonical and grand canonical ensemble Suppose an ideal gas of non-interacting particles with ¯xed particle number N is trapped in a box with a volume V and at equilibrium temperature T . We assume a particle system somehow establishes an equilibrium temperature in spite of the absence of interaction. Such a system can be characterized by the thermodynamic partition function of canonical ensemble X Z = e¡¯ER ; (3.1) R where R stands for a macroscopic state of the gas and is uniquely speci¯ed by the occupa- tion number ni of each single particle state i: fn0; n1; ¢ ¢ ¢ ¢ ¢ ¢g. ¯ = 1=kBT is a temperature parameter. Then, the total energy of a macroscopic state R is given by only the kinetic energy: X ER = "ini; (3.2) i where "i is the eigen-energy of the single particle state i and the occupation number ni satis¯es the normalization condition X N = ni: (3.3) i 1 The probability
    [Show full text]
  • Forecasting of Thunderstorms in the Pre-Monsoon Season at Delhi
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Publications of the IAS Fellows Meteorol. Appl. 6, 29–38 (1999) Forecasting of thunderstorms in the pre-monsoon season at Delhi N Ravi1, U C Mohanty1, O P Madan1 and R K Paliwal2 1Centre for Atmospheric Sciences, Indian Institute of Technology, New Delhi 110 016, India 2National Centre for Medium Range Weather Forecasting, Mausam Bhavan Complex, Lodi Road, New Delhi 110 003, India Accurate prediction of thunderstorms during the pre-monsoon season (April–June) in India is essential for human activities such as construction, aviation and agriculture. Two objective forecasting methods are developed using data from May and June for 1985–89. The developed methods are tested with independent data sets of the recent years, namely May and June for the years 1994 and 1995. The first method is based on a graphical technique. Fifteen different types of stability index are used in combinations of different pairs. It is found that Showalter index versus Totals total index and Jefferson’s modified index versus George index can cluster cases of occurrence of thunderstorms mixed with a few cases of non-occurrence along a zone. The zones are demarcated and further sub-zones are created for clarity. The probability of occurrence/non-occurrence of thunderstorms in each sub-zone is then calculated. The second approach uses a multiple regression method to predict the occurrence/non- occurrence of thunderstorms. A total of 274 potential predictors are subjected to stepwise screening and nine significant predictors are selected to formulate a multiple regression equation that gives the forecast in probabilistic terms.
    [Show full text]
  • לב שלם Siddur Lev Shalem לשבת ויום טוב for Shabbat & FESTIVALS
    סדור לב שלם Siddur Lev Shalem לשבת ויום טוב for shabbat & fEstIVaLs For restricted use only: March-April 2020 Do not copy, sell, or distribute the rabbinical assembly Copyright © 2016 by The Rabbinical Assembly, Inc. First edition. All rights reserved. No part of this book may be reproduced or transmitted in any form The Siddur Lev Shalem Committee or by any means, electronic or mechanical, including photocopy, recording or any information storage or retrieval system, except Rabbi Edward Feld, Senior Editor and Chair for brief passages in connection with a critical review, without permission in writing from: Rabbi Jan Uhrbach, Associate Editor The Rabbinical Assembly Rabbi David M. Ackerman 3080 Broadway New York, NY 10027 Ḥazzan Joanna Dulkin www.rabbinicalassembly.org Rabbi Amy Wallk Katz Permissions and copyrights for quoted materials may be found on pages 463–465. Rabbi Cantor Lilly Kaufman isbn: 978-0-916219-64-2 Rabbi Alan Lettofsky Library of Congress Cataloging-in-Publication Data is available. Rabbi Robert Scheinberg Designed, composed, and produced by Scott-Martin Kosofsky at The Philidor Company, Rabbi Carol Levithan, ex officio Rhinebeck, New York. www.philidor.com The principal Hebrew type, Milon (here in its second and third Rabbi Julie Schonfeld, ex officio iterations), was designed and made by Scott-Martin Kosofsky; it was inspired by the work of Henri Friedlaender. The principal roman and italic is Rongel, by Mário Feliciano; the sans serif is Cronos, by Robert Slimbach. The Hebrew sans serif is Myriad Hebrew, by Robert Slimbach with Scott-Martin Kosofsky. Printed and bound by LSC Communications, Crawfordsville, Indiana.
    [Show full text]
  • Liquid-Vapor Equilibrium in a Binary System
    Liquid-Vapor Equilibria in Binary Systems1 Purpose The purpose of this experiment is to study a binary liquid-vapor equilibrium of chloroform and acetone. Measurements of liquid and vapor compositions will be made by refractometry. The data will be treated according to equilibrium thermodynamic considerations, which are developed in the theory section. Theory Consider a liquid-gas equilibrium involving more than one species. By definition, an ideal solution is one in which the vapor pressure of a particular component is proportional to the mole fraction of that component in the liquid phase over the entire range of mole fractions. Note that no distinction is made between solute and solvent. The proportionality constant is the vapor pressure of the pure material. Empirically it has been found that in very dilute solutions the vapor pressure of solvent (major component) is proportional to the mole fraction X of the solvent. The proportionality constant is the vapor pressure, po, of the pure solvent. This rule is called Raoult's law: o (1) psolvent = p solvent Xsolvent for Xsolvent = 1 For a truly ideal solution, this law should apply over the entire range of compositions. However, as Xsolvent decreases, a point will generally be reached where the vapor pressure no longer follows the ideal relationship. Similarly, if we consider the solute in an ideal solution, then Eq.(1) should be valid. Experimentally, it is generally found that for dilute real solutions the following relationship is obeyed: psolute=K Xsolute for Xsolute<< 1 (2) where K is a constant but not equal to the vapor pressure of pure solute.
    [Show full text]
  • It's Just a Phase!
    BASIS Lesson Plan Lesson Name: It’s Just a Phase! Grade Level Connection(s) NGSS Standards: Grade 2, Physical Science FOSS CA Edition: Grade 3 Physical Science: Matter and Energy Module *Note to teachers: Detailed standards connections can be found at the end of this lesson plan. Teaser/Overview Properties of matter are illustrated through a series of demonstrations and hands-on explorations. Students will learn to identify solids, liquids, and gases. Water will be used to demonstrate the three phases. Students will learn about sublimation through a fun experiment with dry ice (solid CO2). Next, they will compare the propensity of several liquids to evaporate. Finally, they will learn about freezing and melting while making ice cream. Lesson Objectives ● Students will be able to identify the three states of matter (solid, liquid, gas) based on the relative properties of those states. ● Students will understand how to describe the transition from one phase to another (melting, freezing, evaporation, condensation, sublimation) ● Students will learn that matter can change phase when heat/energy is added or removed Vocabulary Words ● Solid: A phase of matter that is characterized by a resistance to change in shape and volume. ● Liquid: A phase of matter that is characterized by a resistance to change in volume; a liquid takes the shape of its container ● Gas: A phase of matter that can change shape and volume ● Phase change: Transformation from one phase of matter to another ● Melting: Transformation from a solid to a liquid ● Freezing: Transformation
    [Show full text]