Modelling the Solar Twin 18 Scorpii? M
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Durham E-Theses
Durham E-Theses First visibility of the lunar crescent and other problems in historical astronomy. Fatoohi, Louay J. How to cite: Fatoohi, Louay J. (1998) First visibility of the lunar crescent and other problems in historical astronomy., Durham theses, Durham University. Available at Durham E-Theses Online: http://etheses.dur.ac.uk/996/ Use policy The full-text may be used and/or reproduced, and given to third parties in any format or medium, without prior permission or charge, for personal research or study, educational, or not-for-prot purposes provided that: • a full bibliographic reference is made to the original source • a link is made to the metadata record in Durham E-Theses • the full-text is not changed in any way The full-text must not be sold in any format or medium without the formal permission of the copyright holders. Please consult the full Durham E-Theses policy for further details. Academic Support Oce, Durham University, University Oce, Old Elvet, Durham DH1 3HP e-mail: [email protected] Tel: +44 0191 334 6107 http://etheses.dur.ac.uk me91 In the name of Allah, the Gracious, the Merciful >° 9 43'' 0' eji e' e e> igo4 U61 J CO J: lic 6..ý v Lo ý , ý.,, "ý J ýs ýºý. ur ý,r11 Lýi is' ý9r ZU LZJE rju No disaster can befall on the earth or in your souls but it is in a book before We bring it into being; that is easy for Allah. In order that you may not grieve for what has escaped you, nor be exultant at what He has given you; and Allah does not love any prideful boaster. -

Livre-Ovni.Pdf
UN MONDE BIZARRE Le livre des étranges Objets Volants Non Identifiés Chapitre 1 Paranormal Le paranormal est un terme utilisé pour qualifier un en- mé n'est pas considéré comme paranormal par les semble de phénomènes dont les causes ou mécanismes neuroscientifiques) ; ne sont apparemment pas explicables par des lois scien- tifiques établies. Le préfixe « para » désignant quelque • Les différents moyens de communication avec les chose qui est à côté de la norme, la norme étant ici le morts : naturels (médiumnité, nécromancie) ou ar- consensus scientifique d'une époque. Un phénomène est tificiels (la transcommunication instrumentale telle qualifié de paranormal lorsqu'il ne semble pas pouvoir que les voix électroniques); être expliqué par les lois naturelles connues, laissant ain- si le champ libre à de nouvelles recherches empiriques, à • Les apparitions de l'au-delà (fantômes, revenants, des interprétations, à des suppositions et à l'imaginaire. ectoplasmes, poltergeists, etc.) ; Les initiateurs de la parapsychologie se sont donné comme objectif d'étudier d'une manière scientifique • la cryptozoologie (qui étudie l'existence d'espèce in- ce qu'ils considèrent comme des perceptions extra- connues) : classification assez injuste, car l'objet de sensorielles et de la psychokinèse. Malgré l'existence de la cryptozoologie est moins de cultiver les mythes laboratoires de parapsychologie dans certaines universi- que de chercher s’il y a ou non une espèce animale tés, notamment en Grande-Bretagne, le paranormal est inconnue réelle derrière une légende ; généralement considéré comme un sujet d'étude peu sé- rieux. Il est en revanche parfois associé a des activités • Le phénomène ovni et ses dérivés (cercle de culture). -

La Photosynthèse Serait Apparue Chez Certains Organismes Primitifs Entre 2.800 Et -2.400 Millions D’Années Si L’On En Croit Certaines Archives Géologiques Terrestres
La photosynthèse serait apparue chez certains organismes primitifs entre 2.800 et -2.400 millions d’années si l’on en croit certaines archives géologiques terrestres. Mais certains la font remonter bien plus tôt en faisant l’hypothèse que les stromatolites que l’on retrouve dans des couches plus anciennes encore sont bien le produit d’une activité biologique. Actuellement, nous n’en sommes sûrs que pour ceux datant de -2.724 millions d’années mais des stromatolites existaient déjà sur Terre il y a 3,5 milliards d’années environ. Quoiqu'il en soit, une certitude demeure, concernant les immenses dépôts de fer du bassin de Hamersley en Australie. Ils datent de l’époque du Sidérien alors que la surface des continents était devenue suffisamment importante pour que se forment des mers peu profondes entourées de grande plates-formes continentales. Les conditions étaient remplies pour que de grands tapis de bactéries construisent des stromatolites en quantités importantes et dégagent massivement de l’oxygène par photosynthèse. Ce gaz corrosif a alors pu oxyder le fer en solution dans les océans et entraîner sa précipitation sous forme d’hydroxyde de fer, de carbonate de fer, de silicate ou de sulfures, selon des variations de l’acidité et du degré d’oxydoréduction de l’eau de mer. C’est ce qu’on appelle la Grande oxydation ou la Catastrophe de l’oxygène. Vers -1.900 millions d’années, la presque totalité du fer présent dans les océans avait précipité et il se retrouve aujourd’hui dans les grands gisements de minerai mondiaux tels que ceux de Hamersley. -

Instrumental Methods for Professional and Amateur
Instrumental Methods for Professional and Amateur Collaborations in Planetary Astronomy Olivier Mousis, Ricardo Hueso, Jean-Philippe Beaulieu, Sylvain Bouley, Benoît Carry, Francois Colas, Alain Klotz, Christophe Pellier, Jean-Marc Petit, Philippe Rousselot, et al. To cite this version: Olivier Mousis, Ricardo Hueso, Jean-Philippe Beaulieu, Sylvain Bouley, Benoît Carry, et al.. Instru- mental Methods for Professional and Amateur Collaborations in Planetary Astronomy. Experimental Astronomy, Springer Link, 2014, 38 (1-2), pp.91-191. 10.1007/s10686-014-9379-0. hal-00833466 HAL Id: hal-00833466 https://hal.archives-ouvertes.fr/hal-00833466 Submitted on 3 Jun 2020 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Instrumental Methods for Professional and Amateur Collaborations in Planetary Astronomy O. Mousis, R. Hueso, J.-P. Beaulieu, S. Bouley, B. Carry, F. Colas, A. Klotz, C. Pellier, J.-M. Petit, P. Rousselot, M. Ali-Dib, W. Beisker, M. Birlan, C. Buil, A. Delsanti, E. Frappa, H. B. Hammel, A.-C. Levasseur-Regourd, G. S. Orton, A. Sanchez-Lavega,´ A. Santerne, P. Tanga, J. Vaubaillon, B. Zanda, D. Baratoux, T. Bohm,¨ V. Boudon, A. Bouquet, L. Buzzi, J.-L. Dauvergne, A. -

Stars and Their Spectra: an Introduction to the Spectral Sequence Second Edition James B
Cambridge University Press 978-0-521-89954-3 - Stars and Their Spectra: An Introduction to the Spectral Sequence Second Edition James B. Kaler Index More information Star index Stars are arranged by the Latin genitive of their constellation of residence, with other star names interspersed alphabetically. Within a constellation, Bayer Greek letters are given first, followed by Roman letters, Flamsteed numbers, variable stars arranged in traditional order (see Section 1.11), and then other names that take on genitive form. Stellar spectra are indicated by an asterisk. The best-known proper names have priority over their Greek-letter names. Spectra of the Sun and of nebulae are included as well. Abell 21 nucleus, see a Aurigae, see Capella Abell 78 nucleus, 327* ε Aurigae, 178, 186 Achernar, 9, 243, 264, 274 z Aurigae, 177, 186 Acrux, see Alpha Crucis Z Aurigae, 186, 269* Adhara, see Epsilon Canis Majoris AB Aurigae, 255 Albireo, 26 Alcor, 26, 177, 241, 243, 272* Barnard’s Star, 129–130, 131 Aldebaran, 9, 27, 80*, 163, 165 Betelgeuse, 2, 9, 16, 18, 20, 73, 74*, 79, Algol, 20, 26, 176–177, 271*, 333, 366 80*, 88, 104–105, 106*, 110*, 113, Altair, 9, 236, 241, 250 115, 118, 122, 187, 216, 264 a Andromedae, 273, 273* image of, 114 b Andromedae, 164 BDþ284211, 285* g Andromedae, 26 Bl 253* u Andromedae A, 218* a Boo¨tis, see Arcturus u Andromedae B, 109* g Boo¨tis, 243 Z Andromedae, 337 Z Boo¨tis, 185 Antares, 10, 73, 104–105, 113, 115, 118, l Boo¨tis, 254, 280, 314 122, 174* s Boo¨tis, 218* 53 Aquarii A, 195 53 Aquarii B, 195 T Camelopardalis, -
![Arxiv:2006.10868V2 [Astro-Ph.SR] 9 Apr 2021 Spain and Institut D’Estudis Espacials De Catalunya (IEEC), C/Gran Capit`A2-4, E-08034 2 Serenelli, Weiss, Aerts Et Al](https://docslib.b-cdn.net/cover/3592/arxiv-2006-10868v2-astro-ph-sr-9-apr-2021-spain-and-institut-d-estudis-espacials-de-catalunya-ieec-c-gran-capit-a2-4-e-08034-2-serenelli-weiss-aerts-et-al-1213592.webp)
Arxiv:2006.10868V2 [Astro-Ph.SR] 9 Apr 2021 Spain and Institut D’Estudis Espacials De Catalunya (IEEC), C/Gran Capit`A2-4, E-08034 2 Serenelli, Weiss, Aerts Et Al
Noname manuscript No. (will be inserted by the editor) Weighing stars from birth to death: mass determination methods across the HRD Aldo Serenelli · Achim Weiss · Conny Aerts · George C. Angelou · David Baroch · Nate Bastian · Paul G. Beck · Maria Bergemann · Joachim M. Bestenlehner · Ian Czekala · Nancy Elias-Rosa · Ana Escorza · Vincent Van Eylen · Diane K. Feuillet · Davide Gandolfi · Mark Gieles · L´eoGirardi · Yveline Lebreton · Nicolas Lodieu · Marie Martig · Marcelo M. Miller Bertolami · Joey S.G. Mombarg · Juan Carlos Morales · Andr´esMoya · Benard Nsamba · KreˇsimirPavlovski · May G. Pedersen · Ignasi Ribas · Fabian R.N. Schneider · Victor Silva Aguirre · Keivan G. Stassun · Eline Tolstoy · Pier-Emmanuel Tremblay · Konstanze Zwintz Received: date / Accepted: date A. Serenelli Institute of Space Sciences (ICE, CSIC), Carrer de Can Magrans S/N, Bellaterra, E- 08193, Spain and Institut d'Estudis Espacials de Catalunya (IEEC), Carrer Gran Capita 2, Barcelona, E-08034, Spain E-mail: [email protected] A. Weiss Max Planck Institute for Astrophysics, Karl Schwarzschild Str. 1, Garching bei M¨unchen, D-85741, Germany C. Aerts Institute of Astronomy, Department of Physics & Astronomy, KU Leuven, Celestijnenlaan 200 D, 3001 Leuven, Belgium and Department of Astrophysics, IMAPP, Radboud University Nijmegen, Heyendaalseweg 135, 6525 AJ Nijmegen, the Netherlands G.C. Angelou Max Planck Institute for Astrophysics, Karl Schwarzschild Str. 1, Garching bei M¨unchen, D-85741, Germany D. Baroch J. C. Morales I. Ribas Institute of· Space Sciences· (ICE, CSIC), Carrer de Can Magrans S/N, Bellaterra, E-08193, arXiv:2006.10868v2 [astro-ph.SR] 9 Apr 2021 Spain and Institut d'Estudis Espacials de Catalunya (IEEC), C/Gran Capit`a2-4, E-08034 2 Serenelli, Weiss, Aerts et al. -
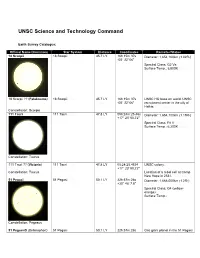
UNSC Science and Technology Command
UNSC Science and Technology Command Earth Survey Catalogue: Official Name/(Common) Star System Distance Coordinates Remarks/Status 18 Scorpii {TCP:p351} 18 Scorpii {Fact} 45.7 LY 16h 15m 37s Diameter: 1,654,100km (1.02R*) {Fact} -08° 22' 06" {Fact} Spectral Class: G2 Va {Fact} Surface Temp.: 5,800K {Fact} 18 Scorpii ?? (Falaknuma) 18 Scorpii {Fact} 45.7 LY 16h 15m 37s UNSC HQ base on world. UNSC {TCP:p351} {Fact} -08° 22' 06" recruitment center in the city of Halkia. {TCP:p355} Constellation: Scorpio 111 Tauri 111 Tauri {Fact} 47.8 LY 05h:24m:25.46s Diameter: 1,654,100km (1.19R*) {Fact} +17° 23' 00.72" {Fact} Spectral Class: F8 V {Fact} Surface Temp.: 6,200K {Fact} Constellation: Taurus 111 Tauri ?? (Victoria) 111 Tauri {Fact} 47.8 LY 05:24:25.4634 UNSC colony. {GoO:p31} {Fact} +17° 23' 00.72" Constellation: Taurus Location of a rebel cell at Camp New Hope in 2531. {GoO:p31} 51 Pegasi {Fact} 51 Pegasi {Fact} 50.1 LY 22h:57m:28s Diameter: 1,668,000km (1.2R*) {Fact} +20° 46' 7.8" {Fact} Spectral Class: G4 (yellow- orange) {Fact} Surface Temp.: Constellation: Pegasus 51 Pegasi-B (Bellerophon) 51 Pegasi 50.1 LY 22h:57m:28s Gas giant planet in the 51 Pegasi {Fact} +20° 46' 7.8" system informally named Bellerophon. Diameter: 196,000km. {Fact} Located on the edge of UNSC territory. {GoO:p15} Its moon, Pegasi Delta, contained a Covenant deuterium/tritium refinery destroyed by covert UNSC forces in 2545. {GoO:p13} Constellation: Pegasus 51 Pegasi-B-1 (Pegasi 51 Pegasi 50.1 LY 22h:57m:28s Moon of the gas giant planet 51 Delta) {GoO:p13} +20° 46' 7.8" Pegasi-B in the 51 Pegasi star Constellation: Pegasus system; a Covenant stronghold on the edge of UNSC territory. -

Southern Stars the JOURNAL of the ROYAL ASTRONOMICAL SOCIETY of NEW ZEALAND P
Southern Stars THE JOURNAL OF THE ROYAL ASTRONOMICAL SOCIETY OF NEW ZEALAND P VolumeVolume 55, No 2 2016 JuneJune ISSN Page0049-1640 1 Royal Astronomical Society Southern Stars of New Zealand (Inc.) Journal of the RASNZ Founded in 1920 as the New Zealand Astronomical Volume 55, Number 2 Society and assumed its present title on receiving the 2016 June Royal Charter in 1946. In 1967 it became a member body of the R oyal Society of New Zealand. CONTENTS P O Box 3181, Wellington 6140, New Zealand Quasars - The Brightest Objects in the Universe [email protected] http://www.rasnz.org.nz Anushka Kharbanda ................................................ 3 Subscriptions (NZ$) for 2016: Norman Dickie ........................................................... 5 Ordinary member: $40.00 Student member: $20.00 Astronomy and Me! Affi liated society: $3.75 per member. Joshua Daglish ........................................................ 6 Minimum $75.00, Maximum $375.00 Corporate member: $200.00 SN 2015lh: Printed copies of Southern Stars (NZ$): The Most Luminous Supernova Discovered $35.00 (NZ) Brent Nicholls .......................................................... 7 $45.00 (Australia & South Pacifi c) $50.00 (Rest of World) The 2015 June 29 Occultation by Pluto Brian Loader .......................................................... 10 Council & Offi cers 2016 to 2018 President: Murray Geddes Prize - Dave Cochrane ................. 17 John Drummond P O Box 113, Patutahi 4045. [email protected] Jennie McCormick - FRASNZ, MNZM .................... 18 Immediate Past President: John Hearnshaw Dep’t Physics & Astronomy, Book Review University of Canterbury, John Drummond ..................................................... 22 Private Bag 4800, Christchurch 8140. [email protected] Vice President: Nicholas Rattenbury The Department of Physics, FRONT COVER The University of Auckland, Brian Loader’s light curve of the Pluto occultation of a th th 38 Princes St, Auckland. -

29:50 Stars, Galaxies, and the Universe First Hour Exam October 6, 2010 Form A
29:50 Stars, Galaxies, and the Universe First Hour Exam October 6, 2010 Form A There are 32 questions. Read through each question and all the answers before choosing. Budget your time. No whining. Walk with Ursus! 1. We can classify stars according to their spectral class and their location on the Hertzsprung Russell diagram. To which class does the Sun belong? (a) K0III (b) O3V (c) M5I (d) G2V ∗ (e) G6III 2. Stars can also be classified according to concentrations or regions on the Hertzsprung Russell diagram. On this basis, the Sun is a (a) Main Sequence star∗ (b) white dwarf star (c) Giant star (d) Supergiant star (e) Cepheid variable 3. It is the day of the vernal equinox. What is the azimuth angle of the Sun when it rises? (a) 0◦ (b) 90◦ ∗ (c) 135◦ (d) 180◦ (e) 270◦ 4. Physically, what is the nature of light? (a) high energy, charged particles emitted by atomic nuclei (b) ripples in the geometry of spacetime (c) concentrated clumps of electric charge (d) strings in higher dimensional space-time (e) a wave of electric and magnetic fields ∗ 1 5. The most basic way to determine the temperature of a star is (a) measuring its apparent magnitude (b) measuring the wavelength at which it is brightest ∗ (c) measuring the absolute magnitude (d) measuring its distance from Earth (e) observing which elements are present via absorption lines 6. Let’s say you are given a number which is the difference between the apparent magnitude and the absolute magnitude of a star. What does that do for you? (a) It tells you the distance to the star. -

From ESPRESSO to PLATO: Detecting and Characterizing Earth-Like Planets in the Presence of Stellar Noise
From ESPRESSO to PLATO: detecting and characterizing Earth-like planets in the presence of stellar noise Tese de Doutouramento Luisa Maria Serrano Departamento de Fisica e Astronomia do Porto, Faculdade de Ciências da Universidade do Porto Orientador: Nuno Cardoso Santos, Co-Orientadora: Susana Cristina Cabral Barros March 2020 Dedication This Ph.D. thesis is the result of 4 years of work, stress, anxiety, but, over all, fun, curiosity and desire of exploring the most hidden scientific discoveries deserved by Astrophysics. Working in Exoplanets was the beginning of the realization of a life-lasting dream, it has allowed me to enter an extremely active and productive group. For this reason my thanks go, first of all, to the ’boss’ and my Ph.D. supervisor, Nuno Santos. He allowed me to be here and introduced me in this world, a distant mirage for the master student from a university where there was no exoplanets thematic line. I also have to thank him for his humanity, not a common quality among professors. The second thank goes to Susana, who was always there for me when I had issues, not necessarily scientific ones. I finally have to thank Mahmoud; heis not listed as supervisor here, but he guided me, teaching me how to do research and giving me precious life lessons, which made me growing. There is also a long series of people I am thankful to, for rendering this years extremely interesting and sustaining me in the deepest moments. My first thought goes to my parents: they were thousands of kilometers far away from me, though they never left me alone and they listened to my complaints, joy, sadness...everything. -

3D Stellar Wind Structure and Radio Emission
MNRAS 000,1{15 (2018) Preprint 17 June 2019 Compiled using MNRAS LATEX style file v3.0 The Solar Wind in Time II: 3D stellar wind structure and radio emission D. O´ Fionnag´ain1y , A. A. Vidotto1, P. Petit2;3, C. P. Folsom2;3, S. V. Jeffers4 , S. C. Marsden5, J. Morin6, J.-D. do Nascimento Jr.7;8, and the BCool Collaboration 1School of Physics, Trinity College Dublin, College Green, Dublin 2, Ireland 2Universit´ede Toulouse, UPS-OMP, Institut de Recherche en Astrophysique et Plan´etologie, Toulouse, France 3IRAP, Universit´ede Toulouse, CNRS, UPS, CNES, 31400, Toulouse, France 4Universit¨at G¨ottingen, Institut fur¨ Astrophysik, Friedrich-Hund-Platz 1, 37077 G¨ottingen, Germany 5University of Southern Queensland, Centre for Astrophysics, Toowoomba, QLD, 4350, Australia 6Laboratoire Univers et Particules de Montpellier, Universit´ede Montpellier, CNRS, F-34095, France 7Dep. de F´ısica, Universidade Federal do Rio Grande do Norte, CEP: 59072-970 Natal, RN, Brazil 8Harvard-Smithsonian Center for Astrophysics, Cambridge, MA 02138, USA Accepted XXX. Received YYY; in original form ZZZ ABSTRACT In this work, we simulate the evolution of the solar wind along its main sequence lifetime and compute its thermal radio emission. To study the evolution of the so- lar wind, we use a sample of solar mass stars at different ages. All these stars have observationally-reconstructed magnetic maps, which are incorporated in our 3D mag- netohydrodynamic simulations of their winds. We show that angular-momentum loss and mass-loss rates decrease steadily on evolutionary timescales, although they can vary in a magnetic cycle timescale. Stellar winds are known to emit radiation in the form of thermal bremsstrahlung in the radio spectrum. -

Extrasolar Planets and Their Host Stars
Kaspar von Braun & Tabetha S. Boyajian Extrasolar Planets and Their Host Stars July 25, 2017 arXiv:1707.07405v1 [astro-ph.EP] 24 Jul 2017 Springer Preface In astronomy or indeed any collaborative environment, it pays to figure out with whom one can work well. From existing projects or simply conversations, research ideas appear, are developed, take shape, sometimes take a detour into some un- expected directions, often need to be refocused, are sometimes divided up and/or distributed among collaborators, and are (hopefully) published. After a number of these cycles repeat, something bigger may be born, all of which one then tries to simultaneously fit into one’s head for what feels like a challenging amount of time. That was certainly the case a long time ago when writing a PhD dissertation. Since then, there have been postdoctoral fellowships and appointments, permanent and adjunct positions, and former, current, and future collaborators. And yet, con- versations spawn research ideas, which take many different turns and may divide up into a multitude of approaches or related or perhaps unrelated subjects. Again, one had better figure out with whom one likes to work. And again, in the process of writing this Brief, one needs create something bigger by focusing the relevant pieces of work into one (hopefully) coherent manuscript. It is an honor, a privi- lege, an amazing experience, and simply a lot of fun to be and have been working with all the people who have had an influence on our work and thereby on this book. To quote the late and great Jim Croce: ”If you dig it, do it.