Supplementary Chapter: Technical Notes
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Hyōgo Prefecture
Coor din ates: 3 4 °4 1 ′2 6 .9 4 ″N 1 3 5 °1 0′5 9 .08″E Hyōgo Prefecture Hyōgo Prefecture (兵庫県 Hyōgo-ken) is a prefecture of Japan located in the Kansai region on Hyōgo Prefecture Honshu island.[1] The capital is Kobe.[2] 兵庫県 Prefecture Contents Japanese transcription(s) • Japanese 兵庫県 History • Rōmaji Hyōgo-ken Geography Cities Towns Islands National parks Mergers Flag Future mergers Symbol Economy Culture National Treasures of Japan Important Preservation Districts for Groups of Historic Buildings in Japan Museums Education Universities Amagasaki Takarazuka Sanda Nishinomiya Ashiya Kobe Kato Akashi Kakogawa Country Japan Himeji Region Kansai Akō Island Honshu High schools Capital Kobe Sports Government Tourism • Governor Toshizō Ido Festival and events Area Transportation Rail • Total 8,396.13 km2 People movers (3,241.76 sq mi) Road Area rank 12th Expressways Population (November 1, 2011) National highways Ports • Total 5,582,978 Airport • Rank 7th • Density 660/km2 (1,700/sq mi) Notable people Sister regions ISO 3166 JP-28 code See also Notes Districts 8 References Municipalities 41 External links Flower Nojigiku (Chrysanthemum japonense) Tree Camphor tree History (Cinnamomum camphora) Bird Oriental white stork Present-day Hyōgo Prefecture includes the former provinces of Harima, Tajima, Awaji, and parts (Ciconia boyciana) of Tanba and Settsu.[3] Website web.pref.hyogo.lg.jp/fl /english/ (http://web.pre In 1180, near the end of the Heian period, Emperor Antoku, Taira no Kiyomori, and the Imperial f.hyogo.lg.jp/fl/english/) court moved briefly to Fukuhara, in what is now the city of Kobe. -

UCLA Electronic Theses and Dissertations
UCLA UCLA Electronic Theses and Dissertations Title Producing Place, Tradition and the Gods: Mt. Togakushi, Thirteenth through Mid-Nineteenth Centuries Permalink https://escholarship.org/uc/item/90w6w5wz Author Carter, Caleb Swift Publication Date 2014 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA Los Angeles Producing Place, Tradition and the Gods: Mt. Togakushi, Thirteenth through Mid-Nineteenth Centuries A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in Asian Languages and Cultures by Caleb Swift Carter 2014 ABSTRACT OF THE DISSERTATION Producing Place, Tradition and the Gods: Mt. Togakushi, Thirteenth through Mid-Nineteenth Centuries by Caleb Swift Carter Doctor of Philosophy in Asian Languages and Cultures University of California, Los Angeles, 2014 Professor William M. Bodiford, Chair This dissertation considers two intersecting aspects of premodern Japanese religions: the development of mountain-based religious systems and the formation of numinous sites. The first aspect focuses in particular on the historical emergence of a mountain religious school in Japan known as Shugendō. While previous scholarship often categorizes Shugendō as a form of folk religion, this designation tends to situate the school in overly broad terms that neglect its historical and regional stages of formation. In contrast, this project examines Shugendō through the investigation of a single site. Through a close reading of textual, epigraphical, and visual sources from Mt. Togakushi (in present-day Nagano Ken), I trace the development of Shugendō and other religious trends from roughly the thirteenth through mid-nineteenth centuries. This study further differs from previous research insofar as it analyzes Shugendō as a concrete system of practices, doctrines, members, institutions, and identities. -

Lions Club Name District Recognition
LIONS CLUB NAME DISTRICT RECOGNITION AGEO District 330 C Model Club AICHI EMERALD District 334 A Model Club AICHI GRACE District 334 A Model Club AICHI HIMAWARI District 334 A Model Club AICHI SAKURA District 334 A Model Club AIZU SHIOKAWA YUGAWA District 332 D Model Club AIZU WAKAMATSU KAKUJO District 332 D Model Club AIZUBANGE District 332 D Model Club ANDONG District 356 E Model Club ANDONG SONGJUK District 356 E Model Club ANJYO District 334 A Model Club ANSAN JOONGANG District 354 B Model Club ANSUNG NUNGKOOL District 354 B Model Club ANYANG INDUK District 354 B Model Club AOMORI CHUO District 332 A Model Club AOMORI HAKKO District 332 A Model Club AOMORI JOMON District 332 A Model Club AOMORI MAHOROBA District 332 A Model Club AOMORI NEBUTA District 332 A Model Club ARAO District 337 E Model Club ASAHIKAWA District 331 B Model Club ASAHIKAWA HIGASHI District 331 B Model Club ASAHIKAWA NANAKAMADO District 331 B Model Club ASAHIKAWA TAISETSU District 331 B Model Club ASAKA District 330 C Model Club ASAKURA District 337 A Model Club ASHIKAGA District 333 B Model Club ASHIKAGA MINAMI District 333 B Model Club ASHIKAGA NISHI District 333 B Model Club ASHIRO District 332 B Model Club ASHIYA District 335 A Model Club ASHIYA HARMONY District 335 A Model Club ASO District 337 E Model Club ATSUGI MULBERRY District 330 B Model Club AYASE District 330 B Model Club BAIK SONG District 354 H Model Club BANGKOK PRAMAHANAKORN 2018 District 310 C Model Club BAYAN BARU District 308 B2 Model Club BIZEN District 336 B Model Club BUCHEON BOKSAGOL District -

Nagano Regional
JTB-Affiliated Ryokan & Hotels Federation Focusing mainly on Nagano Prefecture Regional Map Nagano Prefecture, where the 1998 winter Olympics were held, is located in the center of Japan. It is connected to Tokyo in the southeast, Nagoya in the southwest, and also to Kyoto and Osaka. To the northeast you can get to Niigata, and to the northwest, you can get to Toyama and Kanazawa. It is extremely convenient to get to any major region of Japan by railroad, or highway bus. From here, you can visit all of the major sightseeing area, and enjoy your visit to Japan. Getting to Nagano Kanazawa Toyama JR Hokuriku Shinkansen Hakuba Iiyama JR Oito Line JR Hokuriku Line Nagano Ueda Karuizawa Limited Express () THUNDER BIRD JR Shinonoi Line JR Hokuriku Matsumoto Chino JR Chuo Line Shinkansen JR Chuo Line Shinjuku Shin-Osaka Kyoto Nagoya Tokyo Narita JR Tokaido Shinkansen O 二ニ〕 kansai Chubu Haneda On-line゜ Booking Hotel/Ryokan & Tour with information in Japan CLICK! CLICK! ~ ●JAPAN iCAN.com SUN 廊 E TOURS 四 ※All photos are images. ※The information in this pamphlet is current as of February 2019. ≫ JTB-Affiliated Ryokan & Hotels Federation ヽ ACCESS NAGANO ヽ Narita International Airport Osaka Haneda(Tokyo ダ(Kansai International International Airport) Airport) Nagoya Snow Monkey (Chubu Centrair The wild monkeys who seem to International Airport) enjoy bathing in the hot springs during the snowy season are enormously popular. Yamanouchi Town, Nagano Prefecture Kenrokuen This Japanese-style garden is Sado ga shima Niigata (Niigata Airport) a representative example of Nikko the Edo Period, with its beauty Niigata This dazzling shrine enshrines and grandeur. -

Effects of Viewing Forest Landscape on Middle-Aged Hypertensive Men
Urban Forestry & Urban Greening 21 (2017) 247–252 Contents lists available at ScienceDirect Urban Forestry & Urban Greening journa l homepage: www.elsevier.com/locate/ufug Original article Effects of viewing forest landscape on middle-aged hypertensive men a,1 a,1,2 b c b Chorong Song , Harumi Ikei , Maiko Kobayashi , Takashi Miura , Qing Li , d e f a,∗ Takahide Kagawa , Shigeyoshi Kumeda , Michiko Imai , Yoshifumi Miyazaki a Center for Environment, Health and Field Sciences, Chiba University, 6-2-1 Kashiwa-no-ha, Kashiwa, Chiba 277-0882, Japan b Department of Hygiene and Public Health, Nippon Medical School, 1-1-5 Sendagi, Bunkyo-Ku, Tokyo 113-8602, Japan c Agematsu Town Office, Industry & Tourism Department, 159-3 Agematsu, Kiso, Nagano 399-5601, Japan d Forestry and Forest Products Research Institute, 1 Matsunosato, Tsukuba, Ibaraki 305-8687, Japan e Nagano Prefectural Kiso Hospital, 6613-4 Kisomachi-fukushima, Nagano 397-8555, Japan f Le Verseau Inc., 3-19-4 Miyasaka, Setagaya-ku, Tokyo 156-0051, Japan a r t i c l e i n f o a b s t r a c t Article history: With increasing attention on the health benefits of a forest environment, evidence-based research is Received 13 June 2016 required. This study aims to provide scientific evidence concerning the physiological and psychological Received in revised form 6 December 2016 effects of exposure to the forest environment on middle-aged hypertensive men. Twenty participants Accepted 18 December 2016 (58.0 ± 10.6 years) were instructed to sit on chairs and view the landscapes of forest and urban (as control) Available online 28 December 2016 environments for 10 min. -
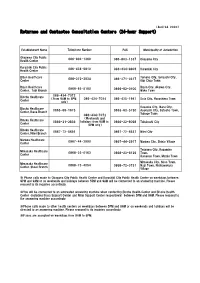
Returnee and Contactee Consultation Centers (24-Hour Support)
(April 24, 2020) Returnee and Contactee Consultation Centers (24-hour Support) Establishment Name Telephone Number FAX Municipality of Jurisdiction Okayama City Public 086-803-1360 086-803-1337 Okayama City Health Center Kurashiki City Public 086-434-9810 086-434-9805 Kurashiki City Health Center Bizen Healthcare Tamano City、Setouchi City、 086-272-3934 086-271-0317 Center Kibi Chuo Town Bizen Healthcare Bizen City、Akaiwa City、 0869-92-5180 0869-92-0100 Center, Tobi Branch Wake Town 086-434-7072 Bicchu Healthcare (From 9AM to 5PM 086-434-7024 086-425-1941 Soja City、Hayashima Town Center only) Kasaoka City、Ibara City、 Bicchu Healthcare 0865-69-1675 0865-63-5750 Asakuchi City、Satosho Town、 Center, Ikasa Branch Yakage Town 086-434-7072 (Weekends and Bihoku Healthcare 0866-21-2836holidays: from 9AM to 0866-22-8098 Takahashi City Center 5PM only) Bihoku Healthcare 0867-72-5691 0867-72-8537 Niimi City Center, Niimi Branch Maniwa Healthcare 0867-44-2990 0867-44-2917 Maniwa City、Shinjo Village Center Tsuyama City、Kagamino Mimasaka Healthcare 0868-23-0163 0868-23-6129 Town、 Center Kumenan Town、Misaki Town Mimasaka City、Shoo Town、 Mimasaka Healthcare 0868-73-4054 0868-72-3731 Nagi Town、Nishiawakura Center, Shoei Branch Village ※ Phone calls made to Okayama City Public Health Center and Kurashiki City Public Health Center on weekdays between 9PM and 9AM or on weekends and holidays between 5PM and 9AM will be connected to an answering machine. Please respond to its inquiries accordingly. ※You will be connected to an automated answering machine when contacting Bicchu Health Center and Bihoku Health Center (including Ikasa Support Center and Niimi Support Center respectively) between 5PM and 9AM. -

Aichi Prefecture
Coordinates: 35°10′48.68″N 136°54′48.63″E Aichi Prefecture 愛 知 県 Aichi Prefecture ( Aichi-ken) is a prefecture of Aichi Prefecture Japan located in the Chūbu region.[1] The region of Aichi is 愛知県 also known as the Tōkai region. The capital is Nagoya. It is the focus of the Chūkyō metropolitan area.[2] Prefecture Japanese transcription(s) • Japanese 愛知県 Contents • Rōmaji Aichi-ken History Etymology Geography Cities Towns and villages Flag Symbol Mergers Economy International relations Sister Autonomous Administrative division Demographics Population by age (2001) Transport Rail People movers and tramways Road Airports Ports Education Universities Senior high schools Coordinates: 35°10′48.68″N Sports 136°54′48.63″E Baseball Soccer Country Japan Basketball Region Chūbu (Tōkai) Volleyball Island Honshu Rugby Futsal Capital Nagoya Football Government Tourism • Governor Hideaki Ōmura (since Festival and events February 2011) Notes Area References • Total 5,153.81 km2 External links (1,989.90 sq mi) Area rank 28th Population (May 1, 2016) History • Total 7,498,485 • Rank 4th • Density 1,454.94/km2 Originally, the region was divided into the two provinces of (3,768.3/sq mi) Owari and Mikawa.[3] After the Meiji Restoration, Owari and ISO 3166 JP-23 Mikawa were united into a single entity. In 187 1, after the code abolition of the han system, Owari, with the exception of Districts 7 the Chita Peninsula, was established as Nagoya Prefecture, Municipalities 54 while Mikawa combined with the Chita Peninsula and Flower Kakitsubata formed Nukata Prefecture. Nagoya Prefecture was renamed (Iris laevigata) to Aichi Prefecture in April 187 2, and was united with Tree Hananoki Nukata Prefecture on November 27 of the same year. -

LIST of the WOOD PACKAGING MATERIAL PRODUCER for EXPORT 2007/2/10 Registration Number Registered Facility Address Phone
LIST OF THE WOOD PACKAGING MATERIAL PRODUCER FOR EXPORT 2007/2/10 Registration number Registered Facility Address Phone 0001002 ITOS CORPORATION KAMOME-JIGYOSHO 62-1 KAMOME-CHO NAKA-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-622-1421 ASAGAMI CORPORATION YOKOHAMA BRANCH YAMASHITA 0001004 279-10 YAMASHITA-CHO NAKA-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-651-2196 OFFICE 0001007 SEITARO ARAI & CO., LTD. TORIHAMA WAREHOUSE 12-57 TORIHAMA-CHO KANAZAWA-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-774-6600 0001008 ISHIKAWA CO., LTD. YOKOHAMA FACTORY 18-24 DAIKOKU-CHO TSURUMI-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-521-6171 0001010 ISHIWATA SHOTEN CO., LTD. 4-13-2 MATSUKAGE-CHO NAKA-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-641-5626 THE IZUMI EXPRESS CO., LTD. TOKYO BRANCH, PACKING 0001011 8 DAIKOKU-FUTO TSURUMI-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-504-9431 CENTER C/O KOUEI-SAGYO HONMOKUEIGYOUSHO, 3-1 HONMOKU-FUTO NAKA-KU 0001012 INAGAKI CO., LTD. HONMOKU B-2 CFS 045-260-1160 YOKOHAMA-SHI KANAGAWA, JAPAN 0001013 INOUE MOKUZAI CO., LTD. 895-3 SYAKE EBINA-SHI KANAGAWA, JAPAN 046-236-6512 0001015 UTOC CORPORATION T-1 OFFICE 15 DAIKOKU-FUTO TSURUMI-KU YOKOHAMA-SHI KANAGAWA, JAPAN 045-501-8379 0001016 UTOC CORPORATION HONMOKU B-1 OFFICE B-1, HONMOKU-FUTOU, NAKA-KU, YOKOHAMA-SHI, KANAGAWA, JAPAN 045-621-5781 0001017 UTOC CORPORATION HONMOKU D-5 CFS 1-16, HONMOKU-FUTOU, NAKA-KU, YOKOHAMA-SHI, KANAGAWA, JAPAN 045-623-1241 0001018 UTOC CORPORATION HONMOKU B-3 OFFICE B-3, HONMOKU-FUTOU, NAKA-KU, YOKOHAMA-SHI, KANAGAWA, JAPAN 045-621-6226 0001020 A.B. SHOUKAI CO., LTD. -
Inazawa City Tour Guide Booklet Inazawa Harmony of Five So
Inazawa City Tour Guide Booklet Inazawa Harmony of Five So All you want to know about sightseeing in Inazawa is in this booklet with handy maps!! Map to Inazawa City HOKURIKU EXPWAY Oyabetonami JCT Kanazawa Takayama Nagano Main Line NAGANO EXPWY Hokuriku TOKAI-HOKURIKU EXPWY Main Line Chuo Main Line Okaya JCT CHUO EXPWY Tokyo Ichinomiya- TOKAI-KANJO EXPWY Nishi IC TOMEI EXPWY Ichinomiya IC MEISHIN EXPWY SHIN-TOMEI EXPWY Inazawa Komaki JCT Suita JCT Nagoya Shizuoka City Toyota JCT Yokkaichi JCT ISE-WANGAN Tokaido Main Line Kameyama JCT EXPWY SHIN-MEISHIN EXPWY Osaka Tokaido Shinkansen HIGASHI-MEIHAN EXPWY Chubu Centrair International Airport Fukuoka / Okinawa Sendai / Sapporo By train Tokyo Nagoya Inazawa Tokaido Shinkansen Tokaido Main Line 1 hr. and 40 min. by "NOZOMI" 10 min. by Local Shin-Osaka Konomiya Tokaido Shinkansen Meitetsu Nagoya Main Line 52 min. by "NOZOMI" 12 min. by Limited Express Kanazawa Gifu Inazawa Hokuriku Main Line / Tokaido Main Line Tokaido Main Line 2 hr. and 36 min. 15 min. by Local by Limited Express "SHIRASAGI" By car Ichinomiya Ichinomiya- Suita JCT JCT Nishi IC Inazawa City Komaki JCT Okaya JCT MEISHIN TOKAI-HOKURIKU 15 min. CHUO EXPWY EXPWY EXPWY 135 min. 120 min. 1 min. Kameyama Ichinomiya Suita JCT JCT Kanie IC IC SHIN-MEISHIN HIGASHI-MEIHAN 20 min. 20 min. MEISHIN EXPWY EXPWY EXPWY 10 min. 70 min. 35 min. Oyabetonami Shizuoka JCT Bisai IC IC TOKAI-HOKURIKU EXPWY 20 min. TOMEI EXPWY 150 min. 140 min. By air Sapporo Chubu Centrair International Airport 1 hr. and 55 min. Sendai Express Konomiya 1 hr. -

Disaster Preparedness for Natural Hazards in Japan (Case Studying in Hyogo Prefecture)
Disaster Preparedness for Natural Hazards in Japan (Case Studying in Hyogo Prefecture) By N.P. Madawan Arachchi (Fulfillment of Visiting Researcher Program in Asian Disaster Reduction Center, Kobe, Japan) N.P Madawan Arachchi Visiting Researcher (Aug-Nov2014) ADRC I Acknowledgement First and foremost, I would like to express my sincere gratitude and lots of thanks Mr. Kiyoshi NATORI, Executive Director of ADRC offering me this valuable opportunity to helping member countries to develop the human resource capacity of officers who are involving in disaster risk management activities. Thank you Sir. I would like to offer my sincere thanks Ms. Yumi Shiomi– Senior Researcher of Asian Disaster Reduction Center (ADRC) as coordinator of this program giving valuable service to every time and supporting all the time beyond the expected. She had done a best hospitality during our memorable stay in Japan and fully involved in our research activities during the program. I offer my special thanks Mr. Makoto Ikeda, Mentor, helping me greatly to be success this research program. He helped me giving advice and doing translation which was most difficult task I have faced for finding and delivering information. Sir, I appreciate your valuable service. Further, I offer my gratitude to all staff members of ADRC giving supports and helping me all the time in numerous manners. Specially Senior Researchers, Researchers, Administrative and supporting staffs. I remind your valuable, memorable service giving us during staying in beautiful Japan. An appreciation and best regards to our Japanese Teacher (Sensei) Mr. Shoji Kawahara, being a good talented teacher that always passionate to teach us the Japanese’s language, culture, foods and others important information. -

Title the CAMPAIGN of PETITIONING for the INAUGURATION
THE CAMPAIGN OF PETITIONING FOR THE INAUGURATION OF A NATIONAL DIET-THE Title PROCESS OF THE ORGANIZATION OF THE SANYO LIBERAL PARTY- Author(s) Naito, Seichu Citation Kyoto University Economic Review (1957), 27(1): 32-52 Issue Date 1957-04 URL https://doi.org/10.11179/ker1926.27.32 Right Type Departmental Bulletin Paper Textversion publisher Kyoto University VOLUME XXVII NUMBER 1 Kyoto University Economic Review MEMOIRS OF THE FACULTY OF ECONOMICS IN THE KYOTO UNIVERSITY THE ECONOMIC THEORY CONCIEVED BY MAX WEBER YU"zo DEGUCHI I TECHNICAL COMPLEMENTARITY IN LINEAR PROGRAMMING Tadashi IMAGAWA 14 THE CAMPAIGN OF PETITIONING FOR THE INAUGURATION OF A NATIONAL DIET Seichii. NAITO 32 ON THE COMMERCIAL ACTIVITIES OF THE MONGOLS IN THE EARLY YEARS OF YUAN DYNASTY Koichi ITO 53 APRIL. 1957 PUBLISHED BY THE F ACUL TY OF ECONOMICS KYOTO UNIVERSITY • KYOTO, JAPAN THE CAMPAIGN OF PETITIONING FOR THE INAUGURATION OF A NATIONAL DIET -THE PROCESS OF THE ORGANIZATION OF THE SANYO LIBERAL PARTY- By SeichU NAITO* .FOREWORD The year 1880 saw the upsurging clamor for liberty and popular rights being consolidated into a nationwide movement for demanding a speedy inauguration of a National Diet at the same time that various layers of the nation continued to have their respective class interests promoted. This was highly significant in the historical process of the Japanese nation in that it marked the first instance of a nationally organized resistance against the contemporary ruling authority. As the prevailing clamor for liberty and popular rights was organized into a vast movement on a national scale embracing all classes of the people, it marked· a significant development for it was intrinsically distinguishable from the sporadic farmers' rebellious uprisings which were often recorded during the ancien regime, and, seen in this light, the movement for liberty and popular rights would well be de fined as a democratic revolutionary movement. -

Pacifico Energy Commences Construction of Japan's Largest Solar Power Plant
Pacifico Energy Commences Construction of Japan's Largest Solar Power Plant April 20, 2017 Pacifico Energy K.K. (Head Office: Minato, Tokyo) is pleased to announce the commencement of construction on Japan's largest solar power generation plant, the 257.7 MW (DC) Sakuto Mega Solar Power Plant in Mimasaka, Okayama. The plant will be constructed on land in Mimasaka City, Okayama Prefecture that was previously the proposed site of the Sakuto St.Valentine Resort and the former site of the Peninsula Golf Club's Yunogo Course (approx. 400ha). Operations are expected to start in September 2019, representing a 30 month construction period. Once commissioned, the plant will generate approximately 290 million kilowatt hours of electricity annually, representing an annual reduction of approximately 200,000 tonnes of CO2 emissions. Chugoku Electric Power Company (CEPCO) will purchase all electricity generated by the plant. Pacifico Energy has already completed construction of two other solar power plants in Okayama (in Kumenan and Mimasaka), which are both now in commercial operation, so the Sakuto Mega Solar Power Plant will be the third project for Pacifico Energy in Okayama. Leveraging know-how and experience gained through developing, constructing, and operating utility scale solar power plants all over the world, we shall continue constructing power plants that contribute to the development of regional communities in an environmentally friendly way. Rendering of completed Sakuto Power plant About Pacifico Energy K.K. : Founded in 2012 to help meet Japan’s domestic energy needs, Pacifico Energy currently has 3 commissioned solar plants in Japan (total capacity: 131 MW (DC)) and is developing more projects, including another 96 MW (DC) currently under construction in Miyazaki.