The Higgs Particles in the MSSM
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
Download -.:: Natural Sciences Publishing
Quant. Phys. Lett. 5, No. 3, 33-47 (2016) 33 Quantum Physics Letters An International Journal http://dx.doi.org/10.18576/qpl/050302 About Electroweak Symmetry Breaking, Electroweak Vacuum and Dark Matter in a New Suggested Proposal of Completion of the Standard Model In Terms Of Energy Fluctuations of a Timeless Three-Dimensional Quantum Vacuum Davide Fiscaletti* and Amrit Sorli SpaceLife Institute, San Lorenzo in Campo (PU), Italy. Received: 21 Sep. 2016, Revised: 18 Oct. 2016, Accepted: 20 Oct. 2016. Published online: 1 Dec. 2016. Abstract: A model of a timeless three-dimensional quantum vacuum characterized by energy fluctuations corresponding to elementary processes of creation/annihilation of quanta is proposed which introduces interesting perspectives of completion of the Standard Model. By involving gravity ab initio, this model allows the Standard Model Higgs potential to be stabilised (in a picture where the Higgs field cannot be considered as a fundamental physical reality but as an emergent quantity from most elementary fluctuations of the quantum vacuum energy density), to generate electroweak symmetry breaking dynamically via dimensional transmutation, to explain dark matter and dark energy. Keywords: Standard Model, timeless three-dimensional quantum vacuum, fluctuations of the three-dimensional quantum vacuum, electroweak symmetry breaking, dark matter. 1 Introduction will we discover beyond the Higgs door? In the Standard Model with a light Higgs boson, an The discovery made by ATLAS and CMS at the Large important problem is that the electroweak potential is Hadron Collider of the 126 GeV scalar particle, which in destabilized by the top quark. Here, the simplest option in the light of available data can be identified with the Higgs order to stabilise the theory lies in introducing a scalar boson [1-6], seems to have completed the experimental particle with similar couplings. -

The Pev-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability
The PeV-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability Waqas Ahmed ? 1, Adeel Mansha ? 2, Tianjun Li ? ~ 3, Shabbar Raza ∗ 4, Joydeep Roy ? 5, Fang-Zhou Xu ? 6, ? CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, P. R. China ~School of Physical Sciences, University of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing 100049, P. R. China ∗ Department of Physics, Federal Urdu University of Arts, Science and Technology, Karachi 75300, Pakistan Institute of Modern Physics, Tsinghua University, Beijing 100084, China Abstract The null results of the LHC searches have put strong bounds on new physics scenario such as supersymmetry (SUSY). With the latest values of top quark mass and strong coupling, we study the upper bounds on the sfermion masses in Split-SUSY from the observed Higgs boson mass and electroweak (EW) vacuum stability. To be consistent with the observed Higgs mass, we find that the largest value of supersymmetry breaking 3 1:5 scales MS for tan β = 2 and tan β = 4 are O(10 TeV) and O(10 TeV) respectively, thus putting an upper bound on the sfermion masses around 103 TeV. In addition, the Higgs quartic coupling becomes negative at much lower scale than the Standard Model (SM), and we extract the upper bound of O(104 TeV) on the sfermion masses from EW vacuum stability. Therefore, we obtain the PeV-Scale Split-SUSY. The key point is the extra contributions to the Renormalization Group Equation (RGE) running from arXiv:1901.05278v1 [hep-ph] 16 Jan 2019 the couplings among Higgs boson, Higgsinos, and gauginos. -

Supersymmetric Dark Matter
Supersymmetric dark matter G. Bélanger LAPTH- Annecy Plan | Dark matter : motivation | Introduction to supersymmetry | MSSM | Properties of neutralino | Status of LSP in various SUSY models | Other DM candidates z SUSY z Non-SUSY | DM : signals, direct detection, LHC Dark matter: a WIMP? | Strong evidence that DM dominates over visible matter. Data from rotation curves, clusters, supernovae, CMB all point to large DM component | DM a new particle? | SM is incomplete : arbitrary parameters, hierarchy problem z DM likely to be related to physics at weak scale, new physics at the weak scale can also solve EWSB z Stable particle protect by symmetry z Many solutions – supersymmetry is one best motivated alternative to SM | NP at electroweak scale could also explain baryonic asymetry in the universe Relic density of wimps | In early universe WIMPs are present in large number and they are in thermal equilibrium | As the universe expanded and cooled their density is reduced Freeze-out through pair annihilation | Eventually density is too low for annihilation process to keep up with expansion rate z Freeze-out temperature | LSP decouples from standard model particles, density depends only on expansion rate of the universe | Relic density | A relic density in agreement with present measurements (Ωh2 ~0.1) requires typical weak interactions cross-section Coannihilation | If M(NLSP)~M(LSP) then maintains thermal equilibrium between NLSP-LSP even after SUSY particles decouple from standard ones | Relic density then depends on rate for all processes -

B2.IV Nuclear and Particle Physics
B2.IV Nuclear and Particle Physics A.J. Barr February 13, 2014 ii Contents 1 Introduction 1 2 Nuclear 3 2.1 Structure of matter and energy scales . 3 2.2 Binding Energy . 4 2.2.1 Semi-empirical mass formula . 4 2.3 Decays and reactions . 8 2.3.1 Alpha Decays . 10 2.3.2 Beta decays . 13 2.4 Nuclear Scattering . 18 2.4.1 Cross sections . 18 2.4.2 Resonances and the Breit-Wigner formula . 19 2.4.3 Nuclear scattering and form factors . 22 2.5 Key points . 24 Appendices 25 2.A Natural units . 25 2.B Tools . 26 2.B.1 Decays and the Fermi Golden Rule . 26 2.B.2 Density of states . 26 2.B.3 Fermi G.R. example . 27 2.B.4 Lifetimes and decays . 27 2.B.5 The flux factor . 28 2.B.6 Luminosity . 28 2.C Shell Model § ............................. 29 2.D Gamma decays § ............................ 29 3 Hadrons 33 3.1 Introduction . 33 3.1.1 Pions . 33 3.1.2 Baryon number conservation . 34 3.1.3 Delta baryons . 35 3.2 Linear Accelerators . 36 iii CONTENTS CONTENTS 3.3 Symmetries . 36 3.3.1 Baryons . 37 3.3.2 Mesons . 37 3.3.3 Quark flow diagrams . 38 3.3.4 Strangeness . 39 3.3.5 Pseudoscalar octet . 40 3.3.6 Baryon octet . 40 3.4 Colour . 41 3.5 Heavier quarks . 43 3.6 Charmonium . 45 3.7 Hadron decays . 47 Appendices 48 3.A Isospin § ................................ 49 3.B Discovery of the Omega § ...................... -
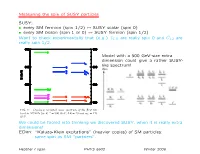
Measuring the Spin of SUSY Particles SUSY: • Every SM Fermion (Spin 1/2
Measuring the spin of SUSY particles SUSY: • every SM fermion (spin 1/2) ↔ SUSY scalar (spin 0) • every SM boson (spin 1 or 0) ↔ SUSY fermion (spin 1/2) Want to check experimentally that (e.g.) eL,R are really spin 0 and Ce1,2 are really spin 1/2. 2 preserve the 5th dimensional momentum (KK number). The corresponding coupling constants among KK modes Model with a 500 GeV-size extra are simply equal to the SM couplings (up to normaliza- tion factors such as √2). The Feynman rules for the KK dimension could give a rather SUSY- modes can easily be derived (e.g., see Ref. [8, 9]). like spectrum! In contrast, the coefficients of the boundary terms are not fixed by Standard Model couplings and correspond to new free parameters. In fact, they are renormalized by the bulk interactions and hence are scale dependent [10, 11]. One might worry that this implies that all pre- dictive power is lost. However, since the wave functions of Standard Model fields and KK modes are spread out over the extra dimension and the new couplings only exist on the boundaries, their effects are volume sup- pressed. We can get an estimate for the size of these volume suppressed corrections with naive dimensional analysis by assuming strong coupling at the cut-off. The FIG. 1: One-loop corrected mass spectrum of the first KK −1 result is that the mass shifts to KK modes from bound- level in MUEDs for R = 500 GeV, ΛR = 20 and mh = 120 ary terms are numerically equal to corrections from loops GeV. -

The Structure of Quarks and Leptons
The Structure of Quarks and Leptons They have been , considered the elementary particles ofmatter, but instead they may consist of still smaller entities confjned within a volume less than a thousandth the size of a proton by Haim Harari n the past 100 years the search for the the quark model that brought relief. In imagination: they suggest a way of I ultimate constituents of matter has the initial formulation of the model all building a complex world out of a few penetrated four layers of structure. hadrons could be explained as combina simple parts. All matter has been shown to consist of tions of just three kinds of quarks. atoms. The atom itself has been found Now it is the quarks and leptons Any theory of the elementary particles to have a dense nucleus surrounded by a themselves whose proliferation is begin fl. of matter must also take into ac cloud of electrons. The nucleus in turn ning to stir interest in the possibility of a count the forces that act between them has been broken down into its compo simpler-scheme. Whereas the original and the laws of nature that govern the nent protons and neutrons. More recent model had three quarks, there are now forces. Little would be gained in simpli ly it has become apparent that the pro thought to be at least 18, as well as six fying the spectrum of particles if the ton and the neutron are also composite leptons and a dozen other particles that number of forces and laws were thereby particles; they are made up of the small act as carriers of forces. -

Higgsino DM Is Dead
Cornering Higgsino at the LHC Satoshi Shirai (Kavli IPMU) Based on H. Fukuda, N. Nagata, H. Oide, H. Otono, and SS, “Higgsino Dark Matter in High-Scale Supersymmetry,” JHEP 1501 (2015) 029, “Higgsino Dark Matter or Not,” Phys.Lett. B781 (2018) 306 “Cornering Higgsino: Use of Soft Displaced Track ”, arXiv:1910.08065 1. Higgsino Dark Matter 2. Current Status of Higgsino @LHC mono-jet, dilepton, disappearing track 3. Prospect of Higgsino Use of soft track 4. Summary 2 DM Candidates • Axion • (Primordial) Black hole • WIMP • Others… 3 WIMP Dark Matter Weakly Interacting Massive Particle DM abundance DM Standard Model (SM) particle 500 GeV DM DM SM Time 4 WIMP Miracle 5 What is Higgsino? Higgsino is (pseudo)Dirac fermion Hypercharge |Y|=1/2 SU(2)doublet <1 TeV 6 Pure Higgsino Spectrum two Dirac Fermions ~ 300 MeV Radiative correction 7 Pure Higgsino DM is Dead DM is neutral Dirac Fermion HUGE spin-independent cross section 8 Pure Higgsino DM is Dead DM is neutral Dirac Fermion Purepure Higgsino Higgsino HUGE spin-independent cross section 9 Higgsino Spectrum (with gaugino) With Gauginos, fermion number is violated Dirac fermion into two Majorana fermions 10 Higgsino Spectrum (with gaugino) 11 Higgsino Spectrum (with gaugino) No SI elastic cross section via Z-boson 12 [N. Nagata & SS 2015] Gaugino induced Observables Mass splitting DM direct detection SM fermion EDM 13 Correlation These observables are controlled by gaugino mass Strong correlation among these observables for large tanb 14 Correlation These observables are controlled by gaugino mass Strong correlation among these observables for large tanb XENON1T constraint 15 Viable Higgsino Spectrum 16 Current Status of Higgsino @LHC 17 Collider Signals of DM p, e- DM DM is invisible p, e+ DM 18 Collider Signals of DM p, e- DM DM is invisible p, e+ DM Additional objects are needed to see DM. -

Higgsino Models and Parameter Determination
Light higgsino models and parameter determination Krzysztof Rolbiecki IFT-CSIC, Madrid in collaboration with: Mikael Berggren, Felix Brummer,¨ Jenny List, Gudrid Moortgat-Pick, Hale Sert and Tania Robens ECFA Linear Collider Workshop 2013 27–31 May 2013, DESY, Hamburg Krzysztof Rolbiecki (IFT-CSIC, Madrid) Higgsino LSP ECFA LC2013, 29 May 2013 1 / 21 SUSY @ LHC What does LHC tell us about 1st/2nd gen. squarks? ! quite heavy Gaugino and stop searches model dependent – limits weaker ATLAS SUSY Searches* - 95% CL Lower Limits ATLAS Preliminary Status: LHCP 2013 ∫Ldt = (4.4 - 20.7) fb-1 s = 7, 8 TeV miss -1 Model e, µ, τ, γ Jets ET ∫Ldt [fb ] Mass limit Reference ~ ~ ~ ~ MSUGRA/CMSSM 0 2-6 jets Yes 20.3 q, g 1.8 TeV m(q)=m(g) ATLAS-CONF-2013-047 ~ ~ ~ ~ MSUGRA/CMSSM 1 e, µ 4 jets Yes 5.8 q, g 1.24 TeV m(q)=m(g) ATLAS-CONF-2012-104 ~ ~ MSUGRA/CMSSM 0 7-10 jets Yes 20.3 g 1.1 TeV any m(q) ATLAS-CONF-2013-054 ~~ ~ ∼0 ~ ∼ qq, q→qχ 0 2-6 jets Yes 20.3 m(χ0 ) = 0 GeV ATLAS-CONF-2013-047 1 q 740 GeV 1 ~~ ~ ∼0 ~ ∼ gg, g→qqχ 0 2-6 jets Yes 20.3 m(χ0 ) = 0 GeV ATLAS-CONF-2013-047 1 g 1.3 TeV 1 ∼± ~ ∼± ~ ∼ ∼ ± ∼ ~ Gluino med. χ (g→qqχ ) 1 e, µ 2-4 jets Yes 4.7 g 900 GeV m(χ 0 ) < 200 GeV, m(χ ) = 0.5(m(χ 0 )+m( g)) 1208.4688 ~~ ∼ ∼ ∼ 1 1 → χ0χ 0 µ ~ χ 0 gg qqqqll(ll) 2 e, (SS) 3 jets Yes 20.7 g 1.1 TeV m( 1 ) < 650 GeV ATLAS-CONF-2013-007 ~ 1 1 ~ GMSB (l NLSP) 2 e, µ 2-4 jets Yes 4.7 g 1.24 TeV tanβ < 15 1208.4688 ~ ~ GMSB (l NLSP) 1-2 τ 0-2 jets Yes 20.7 tanβ >18 ATLAS-CONF-2013-026 Inclusive searches g 1.4 TeV ∼ γ ~ χ 0 GGM (bino NLSP) 2 0 Yes 4.8 -

Electroweak Radiative B-Decays As a Test of the Standard Model and Beyond Andrey Tayduganov
Electroweak radiative B-decays as a test of the Standard Model and beyond Andrey Tayduganov To cite this version: Andrey Tayduganov. Electroweak radiative B-decays as a test of the Standard Model and beyond. Other [cond-mat.other]. Université Paris Sud - Paris XI, 2011. English. NNT : 2011PA112195. tel-00648217 HAL Id: tel-00648217 https://tel.archives-ouvertes.fr/tel-00648217 Submitted on 5 Dec 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. LAL 11-181 LPT 11-69 THESE` DE DOCTORAT Pr´esent´eepour obtenir le grade de Docteur `esSciences de l’Universit´eParis-Sud 11 Sp´ecialit´e:PHYSIQUE THEORIQUE´ par Andrey Tayduganov D´esint´egrationsradiatives faibles de m´esons B comme un test du Mod`eleStandard et au-del`a Electroweak radiative B-decays as a test of the Standard Model and beyond Soutenue le 5 octobre 2011 devant le jury compos´ede: Dr. J. Charles Examinateur Prof. A. Deandrea Rapporteur Prof. U. Ellwanger Pr´esident du jury Prof. S. Fajfer Examinateur Prof. T. Gershon Rapporteur Dr. E. Kou Directeur de th`ese Dr. A. Le Yaouanc Directeur de th`ese Dr. -

Lecture 2 - Energy and Momentum
Lecture 2 - Energy and Momentum E. Daw February 16, 2012 1 Energy In discussing energy in a relativistic course, we start by consid- ering the behaviour of energy in the three regimes we worked with last time. In the first regime, the particle velocity v is much less than c, or more precisely β < 0:3. In this regime, the rest energy ER that the particle has by virtue of its non{zero rest mass is much greater than the kinetic energy T which it has by virtue of its kinetic energy. The rest energy is given by Einstein's famous equation, 2 ER = m0c (1) So, here is an example. An electron has a rest mass of 0:511 MeV=c2. What is it's rest energy?. The important thing here is to realise that there is no need to insert a factor of (3×108)2 to convert from rest mass in MeV=c2 to rest energy in MeV. The units are such that 0.511 is already an energy in MeV, and to get to a mass you would need to divide by c2, so the rest mass is (0:511 MeV)=c2, and all that is left to do is remove the brackets. If you divide by 9 × 1016 the answer is indeed a mass, but the units are eV m−2s2, and I'm sure you will appreciate why these units are horrible. Enough said about that. Now, what about kinetic energy? In the non{relativistic regime β < 0:3, the kinetic energy is significantly smaller than the rest 1 energy. -

The Minimal Supersymmetric Standard Model: Group Summary Report
PM/98–45 December 1998 The Minimal Supersymmetric Standard Model: Group Summary Report Conveners: A. Djouadi1, S. Rosier-Lees2 Working Group: M. Bezouh1, M.-A. Bizouard3,C.Boehm1, F. Borzumati1;4,C.Briot2, J. Carr5,M.B.Causse6, F. Charles7,X.Chereau2,P.Colas8, L. Duflot3, A. Dupperin9, A. Ealet5, H. El-Mamouni9, N. Ghodbane9, F. Gieres9, B. Gonzalez-Pineiro10, S. Gourmelen9, G. Grenier9, Ph. Gris8, J.-F. Grivaz3,C.Hebrard6,B.Ille9, J.-L. Kneur1, N. Kostantinidis5, J. Layssac1,P.Lebrun9,R.Ledu11, M.-C. Lemaire8, Ch. LeMouel1, L. Lugnier9 Y. Mambrini1, J.P. Martin9,G.Montarou6,G.Moultaka1, S. Muanza9,E.Nuss1, E. Perez8,F.M.Renard1, D. Reynaud1,L.Serin3, C. Thevenet9, A. Trabelsi8,F.Zach9,and D. Zerwas3. 1 LPMT, Universit´e Montpellier II, F{34095 Montpellier Cedex 5. 2 LAPP, BP 110, F{74941 Annecy le Vieux Cedex. 3 LAL, Universit´e de Paris{Sud, Bat{200, F{91405 Orsay Cedex 4 CERN, Theory Division, CH{1211, Geneva, Switzerland. 5 CPPM, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. 6 LPC Clermont, Universit´e Blaise Pascal, F{63177 Aubiere Cedex. 7 GRPHE, Universit´e de Haute Alsace, Mulhouse 8 SPP, CEA{Saclay, F{91191 Cedex 9 IPNL, Universit´e Claude Bernard de Lyon, F{69622 Villeurbanne Cedex. 10 LPNHE, Universit´es Paris VI et VII, Paris Cedex. 11 CPT, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. Report of the MSSM working group for the Workshop \GDR{Supersym´etrie". 1 CONTENTS 1. Synopsis 4 2. The MSSM Spectrum 9 2.1 The MSSM: Definitions and Properties 2.1.1 The uMSSM: unconstrained MSSM 2.1.2 The pMSSM: “phenomenological” MSSM 2.1.3 mSUGRA: the constrained MSSM 2.1.4 The MSSMi: the intermediate MSSMs 2.2 Electroweak Symmetry Breaking 2.2.1 General features 2.2.2 EWSB and model–independent tanβ bounds 2.3 Renormalization Group Evolution 2.3.1 The one–loop RGEs 2.3.2 Exact solutions for the Yukawa coupling RGEs 3. -

The Magnetic Dipole Moment of the Muon in Different SUSY Models
The magnetic dipole moment of the muon in different SUSY models Bachelor-Arbeit zur Erlangung des Hochschulgrades Bachelor of Science im Bachelor-Studiengang Physik vorgelegt von Jobst Ziebell geboren am 05.11.1992 in Herrljunga Institut für Kern- und Teilchenphysik Fachrichtung Physik Fakultät Mathematik und Naturwissenschaften Technische Universität Dresden 2015 Eingereicht am 1. Juli 2015 1. Gutachter: Prof. Dr. Dominik Stöckinger 2. Gutachter: Prof. Dr. Kai Zuber Abstract The magnetic dipole moment of the muon is one of the most precisely measured quantities in modern physics. Theory however predicts values that disagree with measurement by several standard deviations [1, Abstract]. Because this may hint at physics beyond the standard model, it is a great opportunity to ex- amine the magnetic dipole moment in different supersymmetric models. It is then possible to calculate dependences of the dipole moment on various model parameters as well as to find constraints for their particular values. The purpose of this paper is to describe how the magnetic dipole moment is obtained in su- persymmetric extensions of the standard model and to document the implementation of its calculation in FlexibleSUSY, a spectrum generator for supersymmetric models [2, Abstract]. Contents 1 Introduction 1 2 The gyromagnetic ratio 2 2.1 In classical mechanics . .2 2.2 In quantum mechanics . .3 2.3 In quantum field theory . .4 3 The implementation in FlexibleSUSY 7 3.1 The C++ part . .7 3.2 The Mathematica part . 11 3.3 The FlexibleSUSY part . 12 4 Results 13 Appendices 17 A The Loop functions . 17 B The VertexFunction template . 17 C The DiagramEvaluator<...>::value() functions .