DOCSLIB.ORG

R-Parity Violation and Light Neutralinos at Ship and the LHC

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
R-Parity Violation and Light Neutralinos at Ship and the LHC BONN-TH-2015-12 R-Parity Violation and Light Neutralinos at SHiP and the LHC Jordy de Vries,1, ∗ Herbi K. Dreiner,2, y and Daniel Schmeier2, z 1Institute for Advanced Simulation, Institut f¨urKernphysik, J¨ulichCenter for Hadron Physics, Forschungszentrum J¨ulich, D-52425 J¨ulich, Germany 2Physikalisches Institut der Universit¨atBonn, Bethe Center for Theoretical Physics, Nußallee 12, 53115 Bonn, Germany We study the sensitivity of the proposed SHiP experiment to the LQD operator in R-Parity vi- olating supersymmetric theories. We focus on single neutralino production via rare meson decays and the observation of downstream neutralino decays into charged mesons inside the SHiP decay chamber. We provide a generic list of effective operators and decay width formulae for any λ0 cou- pling and show the resulting expected SHiP sensitivity for a widespread list of benchmark scenarios via numerical simulations. We compare this sensitivity to expected limits from testing the same decay topology at the LHC with ATLAS. I. INTRODUCTION method to search for a light neutralino, is via the pro- duction of mesons. The rate for the latter is so high, Supersymmetry [1{3] is the unique extension of the ex- that the subsequent rare decay of the meson to the light ternal symmetries of the Standard Model of elementary neutralino via (an) R-parity violating operator(s) can be particle physics (SM) with fermionic generators [4]. Su- searched for [26{28]. This is analogous to the production persymmetry is necessarily broken, in order to comply of neutrinos via π or K-mesons. with the bounds from experimental searches. To solve For a neutralino in the mass range of about 0.5 - 5 GeV, the hierarchy problem [5, 6], the masses of the super- the newly proposed SHiP experimental facility [29] seems symmetric partners of the SM fields should be lighter ideal. It will consist of a high intensity 400 GeV pro- than 1-10 TeV, with a clear preference for lighter fields, ton beam from the CERN SPS incident on a fixed tar- see for example [7{11]. All experimental searches for su- get. 63.8 m down beam line there will a detector for persymmetric particles have hitherto been unsuccessful. long-lived heavy neutral particles. Two of us (HKD, The LHC sets limits on the strongly interacting spar- DS) have performed a preliminary analysis in [30], for ticles, the squarks and gluinos, of order 1 TeV, see for a small set of R-parity violating operators: the decay + 0 + 0 ¯ example [12, 13]. However the limits on the only elec- D ! χ~1 `i via the operator λi21LiQ2D1, and the de- 0 0 ∓ ± 0 troweak interacting particles, such as the sleptons, the caysχ ~1 ! (K ν; K `i ) via λi21;i21. It is the purpose neutralinos and the charginos, are significantly weaker of this paper to extend this to all possible production [14, 15]. In fact, as has been discussed in the literature modes and decay channels, and to determine the search there is currently no lower mass bound on the lightest su- sensitivity of the SHiP experiment. As an example, in persymmetric particle (LSP) neutralino, which is model earlier work [26], the production of B-mesons at NuTeV 0 0 independent [16, 17]. The limits from LEP can easily be was considered. The mesons could decay as Bd;s ! χ~1 ν ± 0 ± 0 avoided, and in particular, a massless neutralino is still or B ! χ~1 `i via λi13. The neutralinos could decay via allowed, for sufficiently heavy selectrons and squarks [18]. the LiQ1D¯ 3 operators, or purely leptonically via LiLjE¯k We discuss this in more detail below, in Sec. III. operators. These scenarios can also be tested at SHiP, We are here interested in the possibilities of searching where a sufficiently large number of B-type mesons is ex- arXiv:1511.07436v1 [hep-ph] 23 Nov 2015 for a light neutralino, up to masses of about 10 GeV. pected and we will show the sensitivity reach to the LQD¯ Already for a slepton mass of 150 GeV there is no sen- operators here. + − 0 0 sitivity via the process e e ! χ~1χ1γ from LEP data This paper is organized as follows. In Sec. II, we briefly [19], see also [20, 21]. Since mass reach is not a factor, review supersymmetry with broken R-parity. We also one might suspect that the high intensity facilities used discuss the bounds on the operators relevant to our anal- as B-factories, would be more sensitive, but this is also ysis. Constraints on the neutralino mass and motiva- not the case [19]. tions for the possibility of a very light neutralino follow In order to avoid over-closing the universe [22{24], a in Sec. III. In Sec. IV we discuss the relevant neutralino 10 GeV or lighter neutralino must decay via R-parity production and decay channels we expect to be most rele- violating operators [25]. If the R-parity violating cou- vant for SHiP observations of R-parity violation (RPV). plings are not too small, in this case, the most promising In Sec. V we set up the effective field theory need to compute the relevant meson and neutralino decays and compute the latter in general fashion. With these re- ∗ [email protected] sults at hand, we specialize to the SHiP set-up in Sec. VI y dreiner@uni{bonn.de and discuss under what circumstances a neutralino could z [email protected]{bonn.de be detected. In Sec. VII we explain the methodology of 2 our numerical study. The discussion of the sensitivity of B. Bounds on R-parity Violating Couplings the SHiP experiment to the existence of light, but unsta- ble, neutralinos in several benchmark scenarios is given The operators LiQjD¯ k which we investigate here all vi- in Sec. VIII. In Sect. IX, we discuss an estimate for pos- olate lepton number; thus there are strict bounds on the sible effects of our benchmark scenarios at the LHC. We 0 coupling constants λijk, see for example the reviews [46{ conclude in Sect. X. 50]. We briefly summarize here the existing bounds on the specific operators which we investigate in our bench- mark scenarios in Sec. VIII. For our results on the sensi- 0 II. R-PARITY VIOLATION tivity reach of SHiP, we focus on the cases λ1jk, involving 0 final state electrons, and λ31k, which produces tau lep- A. Introduction tons. However, experimentally final state muons should be testable at least as well as electrons. We thus also 0 present the corresponding bounds on the couplings λ2jk, The minimal supersymmetric extension of the SM re- which are typically weaker. We take most of the numbers quires the introduction of an additional Higgs doublet. from the most recent review [50]. The minimal set of pure matter couplings are then en- 0 ms~r 0 ms~R coded in the minimal supersymmetric SM (MSSM) su- λ112 < 0:03 ; λ212< 0:06 : (5) perpotential 100 GeV 100 GeV m m ~ ¯ ¯ λ0 < 0:2 c~L ; λ0 < 0:1 dR ; (6) WMSSM = (hE)ijLiHdEj + (hD)ijQiHdDj 121 100 GeV 221 100 GeV +(h ) Q H U¯ + µH H : (1) U ij i u j d u m m λ0 < 0:2 c~L ; λ0 < 0:1 s~R ; (7) 122 100 GeV 222 100 GeV Here hE;D;U are dimensionless 3 × 3 coupling matrices. The Higgs mixing µ has mass dimension one. This su- m~ 0 mt~L 0 bL perpotential is equivalent to imposing the discrete Z λ131 < 0:03 ; λ231< 0:18 ; (8) 2 100 GeV 100 GeV symmetry R-parity [31], or the Z6 proton hexality [32], and results in a stable proton. Both are discrete gauge ms~R λ0 < 0:06 ; (9) anomaly-free, ensuring stability under potential quantum 312 100 GeV gravity corrections [33]. A model restricted to the super- m~ potential W is called R-parity conserving. The ad- 0 tL MSSM λ313 < 0:06 ; (10) vantage is that the LSP, usually the lightest neutralino, is 100 GeV 0 an automatic WIMP dark matter candidate [34]. How- The bound on λ231 is from [48], as there is no bound ever, no such dark matter has been observed to-date, quoted in [50]. Assuming an experimental neutrino mass motivating the search for other forms of supersymmetry. bound mν < 1 eV results in a bound of approximately 0 Instead in R-parity violating models, there are further λ122;222 < 0:01 m=~ 100 GeV [40, 48, 51]. This is how- possible terms in the superpotential ever model dependent, as we know there must be further, possibly off-diagonal,p contributions to the neutrino mass WRPV = WLV + WBV ; (2) matrix. ¯ 0 ¯ WLV = λijkLiLjEk + λijkLiQjDk + κiLiHu ; (3) 00 ¯ ¯ ¯ WBV = λijkUiDjDk : (4) III. A LIGHT NEUTRALINO Imposing the discrete Z3 symmetry baryon triality [32, The best lower mass limit on the lightest supersym- 35], the lepton-number violating terms in WLV remain. metric particle (LSP) neutralino is from LEP [17] The proton remains stable, since baryon-number is con- served, however the neutralino LSP is unstable and is m 0 > 46 GeV: (11) χ~1 no longer a dark matter candidate. This can be solved by introducing the axion to solve the problem of CP- This uses the LEP-II chargino search to restrict the range violation in QCD. The supersymmetric partner, the ax- of µ and the SU(2) soft breaking gaugino mass parameter ino, is then automatically a good dark matter candidate M2 and then assumes the supersymmetric GUT relation [36{39] and light neutrino masses are also generated auto- 5 2 1 matically [40{44].
Load more

Recommended publications
  • PHY323:Lecture 11 SUSY and UED
    PHY323:Lecture 11 SUSY and UED •Higgs and Supersymmetry •The Neutralino •Extra Dimensions •How WIMPs interact Candidates for Dark Matter III The New Particle Zoo Here are a few of the candidates on a plot showing cross section vs. mass. An enormous range. We will focus on WIMPs thanks to L. Roszkowski (Sheffield) Freeze Out of Thermal DM Particles WIMP Candidate 1 Supersymmetric Dark Matter Each particle gets a “sparticle” counterpart. Bosons get fermions and vice versa. e.g. Photon Photino W Wino Z Zino etc The Lightest Supersymmetric Particle (LSP) is predicted to be stable. This is called the NEUTRALINO. Supersymmetry Theory What we are aiming to do, e.g.: At higher energies, where symmetries are unbroken, you might expect a unified theory should have a single coupling constant Supersymmetry Theory and the Higgs To make things simpler, it would be nice if all the forces of nature were unified under the same theoretical framework. The energy at which this is likely called the Planck energy (1019 GeV). This was started in the 1970s - the result is the electroweak theory. The theory is intricate and complicated, partly because the photon is massless, but the W & Z are heavy. The electroweak theory posits that the very different carriers, and therefore properties, of these forces at energy scales present in nature today are actually the result of taking a much more symmteric theory at higher energies, above the ‘electroweak scale’ of 90GeV (the W and Z rest energy) and ‘spontaneously breaking’ it. The theoretical mechanism for spontaneous symmetry breaking requires yet another new particle, a spin zero particle called the HIGGS BOSON.
    [Show full text]
  • CERN Courier–Digital Edition
    CERNMarch/April 2021 cerncourier.com COURIERReporting on international high-energy physics WELCOME CERN Courier – digital edition Welcome to the digital edition of the March/April 2021 issue of CERN Courier. Hadron colliders have contributed to a golden era of discovery in high-energy physics, hosting experiments that have enabled physicists to unearth the cornerstones of the Standard Model. This success story began 50 years ago with CERN’s Intersecting Storage Rings (featured on the cover of this issue) and culminated in the Large Hadron Collider (p38) – which has spawned thousands of papers in its first 10 years of operations alone (p47). It also bodes well for a potential future circular collider at CERN operating at a centre-of-mass energy of at least 100 TeV, a feasibility study for which is now in full swing. Even hadron colliders have their limits, however. To explore possible new physics at the highest energy scales, physicists are mounting a series of experiments to search for very weakly interacting “slim” particles that arise from extensions in the Standard Model (p25). Also celebrating a golden anniversary this year is the Institute for Nuclear Research in Moscow (p33), while, elsewhere in this issue: quantum sensors HADRON COLLIDERS target gravitational waves (p10); X-rays go behind the scenes of supernova 50 years of discovery 1987A (p12); a high-performance computing collaboration forms to handle the big-physics data onslaught (p22); Steven Weinberg talks about his latest work (p51); and much more. To sign up to the new-issue alert, please visit: http://comms.iop.org/k/iop/cerncourier To subscribe to the magazine, please visit: https://cerncourier.com/p/about-cern-courier EDITOR: MATTHEW CHALMERS, CERN DIGITAL EDITION CREATED BY IOP PUBLISHING ATLAS spots rare Higgs decay Weinberg on effective field theory Hunting for WISPs CCMarApr21_Cover_v1.indd 1 12/02/2021 09:24 CERNCOURIER www.
    [Show full text]
  • The Pev-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability
    The PeV-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability Waqas Ahmed ? 1, Adeel Mansha ? 2, Tianjun Li ? ~ 3, Shabbar Raza ∗ 4, Joydeep Roy ? 5, Fang-Zhou Xu ? 6, ? CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, P. R. China ~School of Physical Sciences, University of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing 100049, P. R. China ∗ Department of Physics, Federal Urdu University of Arts, Science and Technology, Karachi 75300, Pakistan Institute of Modern Physics, Tsinghua University, Beijing 100084, China Abstract The null results of the LHC searches have put strong bounds on new physics scenario such as supersymmetry (SUSY). With the latest values of top quark mass and strong coupling, we study the upper bounds on the sfermion masses in Split-SUSY from the observed Higgs boson mass and electroweak (EW) vacuum stability. To be consistent with the observed Higgs mass, we find that the largest value of supersymmetry breaking 3 1:5 scales MS for tan β = 2 and tan β = 4 are O(10 TeV) and O(10 TeV) respectively, thus putting an upper bound on the sfermion masses around 103 TeV. In addition, the Higgs quartic coupling becomes negative at much lower scale than the Standard Model (SM), and we extract the upper bound of O(104 TeV) on the sfermion masses from EW vacuum stability. Therefore, we obtain the PeV-Scale Split-SUSY. The key point is the extra contributions to the Renormalization Group Equation (RGE) running from arXiv:1901.05278v1 [hep-ph] 16 Jan 2019 the couplings among Higgs boson, Higgsinos, and gauginos.
    [Show full text]
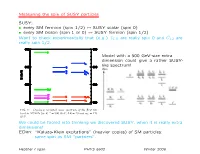
  • Measuring the Spin of SUSY Particles SUSY: • Every SM Fermion (Spin 1/2
    Measuring the spin of SUSY particles SUSY: • every SM fermion (spin 1/2) ↔ SUSY scalar (spin 0) • every SM boson (spin 1 or 0) ↔ SUSY fermion (spin 1/2) Want to check experimentally that (e.g.) eL,R are really spin 0 and Ce1,2 are really spin 1/2. 2 preserve the 5th dimensional momentum (KK number). The corresponding coupling constants among KK modes Model with a 500 GeV-size extra are simply equal to the SM couplings (up to normaliza- tion factors such as √2). The Feynman rules for the KK dimension could give a rather SUSY- modes can easily be derived (e.g., see Ref. [8, 9]). like spectrum! In contrast, the coefficients of the boundary terms are not fixed by Standard Model couplings and correspond to new free parameters. In fact, they are renormalized by the bulk interactions and hence are scale dependent [10, 11]. One might worry that this implies that all pre- dictive power is lost. However, since the wave functions of Standard Model fields and KK modes are spread out over the extra dimension and the new couplings only exist on the boundaries, their effects are volume sup- pressed. We can get an estimate for the size of these volume suppressed corrections with naive dimensional analysis by assuming strong coupling at the cut-off. The FIG. 1: One-loop corrected mass spectrum of the first KK −1 result is that the mass shifts to KK modes from bound- level in MUEDs for R = 500 GeV, ΛR = 20 and mh = 120 ary terms are numerically equal to corrections from loops GeV.
    [Show full text]
  • Electroweak Radiative B-Decays As a Test of the Standard Model and Beyond Andrey Tayduganov
    Electroweak radiative B-decays as a test of the Standard Model and beyond Andrey Tayduganov To cite this version: Andrey Tayduganov. Electroweak radiative B-decays as a test of the Standard Model and beyond. Other [cond-mat.other]. Université Paris Sud - Paris XI, 2011. English. NNT : 2011PA112195. tel-00648217 HAL Id: tel-00648217 https://tel.archives-ouvertes.fr/tel-00648217 Submitted on 5 Dec 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. LAL 11-181 LPT 11-69 THESE` DE DOCTORAT Pr´esent´eepour obtenir le grade de Docteur `esSciences de l’Universit´eParis-Sud 11 Sp´ecialit´e:PHYSIQUE THEORIQUE´ par Andrey Tayduganov D´esint´egrationsradiatives faibles de m´esons B comme un test du Mod`eleStandard et au-del`a Electroweak radiative B-decays as a test of the Standard Model and beyond Soutenue le 5 octobre 2011 devant le jury compos´ede: Dr. J. Charles Examinateur Prof. A. Deandrea Rapporteur Prof. U. Ellwanger Pr´esident du jury Prof. S. Fajfer Examinateur Prof. T. Gershon Rapporteur Dr. E. Kou Directeur de th`ese Dr. A. Le Yaouanc Directeur de th`ese Dr.
    [Show full text]
  • The Minimal Supersymmetric Standard Model: Group Summary Report
    PM/98–45 December 1998 The Minimal Supersymmetric Standard Model: Group Summary Report Conveners: A. Djouadi1, S. Rosier-Lees2 Working Group: M. Bezouh1, M.-A. Bizouard3,C.Boehm1, F. Borzumati1;4,C.Briot2, J. Carr5,M.B.Causse6, F. Charles7,X.Chereau2,P.Colas8, L. Duflot3, A. Dupperin9, A. Ealet5, H. El-Mamouni9, N. Ghodbane9, F. Gieres9, B. Gonzalez-Pineiro10, S. Gourmelen9, G. Grenier9, Ph. Gris8, J.-F. Grivaz3,C.Hebrard6,B.Ille9, J.-L. Kneur1, N. Kostantinidis5, J. Layssac1,P.Lebrun9,R.Ledu11, M.-C. Lemaire8, Ch. LeMouel1, L. Lugnier9 Y. Mambrini1, J.P. Martin9,G.Montarou6,G.Moultaka1, S. Muanza9,E.Nuss1, E. Perez8,F.M.Renard1, D. Reynaud1,L.Serin3, C. Thevenet9, A. Trabelsi8,F.Zach9,and D. Zerwas3. 1 LPMT, Universit´e Montpellier II, F{34095 Montpellier Cedex 5. 2 LAPP, BP 110, F{74941 Annecy le Vieux Cedex. 3 LAL, Universit´e de Paris{Sud, Bat{200, F{91405 Orsay Cedex 4 CERN, Theory Division, CH{1211, Geneva, Switzerland. 5 CPPM, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. 6 LPC Clermont, Universit´e Blaise Pascal, F{63177 Aubiere Cedex. 7 GRPHE, Universit´e de Haute Alsace, Mulhouse 8 SPP, CEA{Saclay, F{91191 Cedex 9 IPNL, Universit´e Claude Bernard de Lyon, F{69622 Villeurbanne Cedex. 10 LPNHE, Universit´es Paris VI et VII, Paris Cedex. 11 CPT, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. Report of the MSSM working group for the Workshop \GDR{Supersym´etrie". 1 CONTENTS 1. Synopsis 4 2. The MSSM Spectrum 9 2.1 The MSSM: Definitions and Properties 2.1.1 The uMSSM: unconstrained MSSM 2.1.2 The pMSSM: “phenomenological” MSSM 2.1.3 mSUGRA: the constrained MSSM 2.1.4 The MSSMi: the intermediate MSSMs 2.2 Electroweak Symmetry Breaking 2.2.1 General features 2.2.2 EWSB and model–independent tanβ bounds 2.3 Renormalization Group Evolution 2.3.1 The one–loop RGEs 2.3.2 Exact solutions for the Yukawa coupling RGEs 3.
    [Show full text]
  • The Magnetic Dipole Moment of the Muon in Different SUSY Models
    The magnetic dipole moment of the muon in different SUSY models Bachelor-Arbeit zur Erlangung des Hochschulgrades Bachelor of Science im Bachelor-Studiengang Physik vorgelegt von Jobst Ziebell geboren am 05.11.1992 in Herrljunga Institut für Kern- und Teilchenphysik Fachrichtung Physik Fakultät Mathematik und Naturwissenschaften Technische Universität Dresden 2015 Eingereicht am 1. Juli 2015 1. Gutachter: Prof. Dr. Dominik Stöckinger 2. Gutachter: Prof. Dr. Kai Zuber Abstract The magnetic dipole moment of the muon is one of the most precisely measured quantities in modern physics. Theory however predicts values that disagree with measurement by several standard deviations [1, Abstract]. Because this may hint at physics beyond the standard model, it is a great opportunity to ex- amine the magnetic dipole moment in different supersymmetric models. It is then possible to calculate dependences of the dipole moment on various model parameters as well as to find constraints for their particular values. The purpose of this paper is to describe how the magnetic dipole moment is obtained in su- persymmetric extensions of the standard model and to document the implementation of its calculation in FlexibleSUSY, a spectrum generator for supersymmetric models [2, Abstract]. Contents 1 Introduction 1 2 The gyromagnetic ratio 2 2.1 In classical mechanics . .2 2.2 In quantum mechanics . .3 2.3 In quantum field theory . .4 3 The implementation in FlexibleSUSY 7 3.1 The C++ part . .7 3.2 The Mathematica part . 11 3.3 The FlexibleSUSY part . 12 4 Results 13 Appendices 17 A The Loop functions . 17 B The VertexFunction template . 17 C The DiagramEvaluator<...>::value() functions .
    [Show full text]
  • Supersymmetric Particle Searches
    Citation: K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014) (URL: http://pdg.lbl.gov) Supersymmetric Particle Searches A REVIEW GOES HERE – Check our WWW List of Reviews A REVIEW GOES HERE – Check our WWW List of Reviews SUPERSYMMETRIC MODEL ASSUMPTIONS The exclusion of particle masses within a mass range (m1, m2) will be denoted with the notation “none m m ” in the VALUE column of the 1− 2 following Listings. The latest unpublished results are described in the “Supersymmetry: Experiment” review. A REVIEW GOES HERE – Check our WWW List of Reviews CONTENTS: χ0 (Lightest Neutralino) Mass Limit 1 e Accelerator limits for stable χ0 − 1 Bounds on χ0 from dark mattere searches − 1 χ0-p elastice cross section − 1 eSpin-dependent interactions Spin-independent interactions Other bounds on χ0 from astrophysics and cosmology − 1 Unstable χ0 (Lighteste Neutralino) Mass Limit − 1 χ0, χ0, χ0 (Neutralinos)e Mass Limits 2 3 4 χe ,eχ e(Charginos) Mass Limits 1± 2± Long-livede e χ± (Chargino) Mass Limits ν (Sneutrino)e Mass Limit Chargede Sleptons e (Selectron) Mass Limit − µ (Smuon) Mass Limit − e τ (Stau) Mass Limit − e Degenerate Charged Sleptons − e ℓ (Slepton) Mass Limit − q (Squark)e Mass Limit Long-livede q (Squark) Mass Limit b (Sbottom)e Mass Limit te (Stop) Mass Limit eHeavy g (Gluino) Mass Limit Long-lived/lighte g (Gluino) Mass Limit Light G (Gravitino)e Mass Limits from Collider Experiments Supersymmetrye Miscellaneous Results HTTP://PDG.LBL.GOV Page1 Created: 8/21/2014 12:57 Citation: K.A. Olive et al.
    [Show full text]
  • Neutralino Dark Matter in Supersymmetric Models with Non--Universal Scalar Mass Terms
    CERN{TH 95{206 DFTT 47/95 JHU{TIPAC 95020 LNGS{95/51 GEF{Th{7/95 August 1995 Neutralino dark matter in sup ersymmetric mo dels with non{universal scalar mass terms. a b,c d e,c b,c V. Berezinsky , A. Bottino , J. Ellis ,N.Fornengo , G. Mignola f,g and S. Scop el a INFN, Laboratori Nazionali del Gran Sasso, 67010 Assergi (AQ), Italy b Dipartimento di FisicaTeorica, UniversitadiTorino, Via P. Giuria 1, 10125 Torino, Italy c INFN, Sezione di Torino, Via P. Giuria 1, 10125 Torino, Italy d Theoretical Physics Division, CERN, CH{1211 Geneva 23, Switzerland e Department of Physics and Astronomy, The Johns Hopkins University, Baltimore, Maryland 21218, USA. f Dipartimento di Fisica, Universita di Genova, Via Dodecaneso 33, 16146 Genova, Italy g INFN, Sezione di Genova, Via Dodecaneso 33, 16146 Genova, Italy Abstract Neutralino dark matter is studied in the context of a sup ergravityscheme where the scalar mass terms are not constrained by universality conditions at the grand uni cation scale. We analyse in detail the consequences of the relaxation of this universality assumption on the sup ersymmetric parameter space, on the neutralino relic abundance and on the event rate for the direct detection of relic neutralinos. E{mail: b [email protected], b [email protected], [email protected], [email protected], [email protected], scop [email protected] 1 I. INTRODUCTION The phenomenology of neutralino dark matter has b een studied extensively in the Mini- mal Sup ersymmetric extension of the Standard Mo del (MSSM) [1].
    [Show full text]
  • Non–Baryonic Dark Matter V
    Non–Baryonic Dark Matter V. Berezinsky1 , A. Bottino2,3 and G. Mignola3,4 1INFN, Laboratori Nazionali del Gran Sasso, 67010 Assergi (AQ), Italy 2Universit`a di Torino, via P. Giuria 1, I-10125 Torino, Italy 3INFN - Sezione di Torino, via P. Giuria 1, I-10125 Torino, Italy 4Theoretical Physics Division, CERN, CH–1211 Geneva 23, Switzerland (presented by V. Berezinsky) The best particle candidates for non–baryonic cold dark matter are reviewed, namely, neutralino, axion, axino and Majoron. These particles are considered in the context of cosmological models with the restrictions given by the observed mass spectrum of large scale structures, data on clusters of galaxies, age of the Universe etc. 1. Introduction (Cosmological environ- The structure formation in Universe put strong ment) restrictions to the properties of DM in Universe. Universe with HDM plus baryonic DM has a Presence of dark matter (DM) in the Universe wrong prediction for the spectrum of fluctuations is reliably established. Rotation curves in many as compared with measurements of COBE, IRAS galaxies provide evidence for large halos filled by and CfA. CDM plus baryonic matter can ex- nonluminous matter. The galaxy velocity distri- plain the spectrum of fluctuations if total density bution in clusters also show the presence of DM in Ω0 ≈ 0.3. intercluster space. IRAS and POTENT demon- There is one more form of energy density in the strate the presence of DM on the largest scale in Universe, namely the vacuum energy described the Universe. by the cosmological constant Λ. The correspond- The matter density in the Universe ρ is usually 2 ing energy density is given by ΩΛ =Λ/(3H0 ).
    [Show full text]
  • Rethinking “Dark Matter” Within the Epistemologically Different World (EDW) Perspective Gabriel Vacariu and Mihai Vacariu
    Chapter Rethinking “Dark Matter” within the Epistemologically Different World (EDW) Perspective Gabriel Vacariu and Mihai Vacariu The really hard problems are great because we know they’ll require a crazy new idea. (Mike Turner in Panek 2011, p. 195) Abstract In the first part of the article, we show how the notion of the “universe”/“world” should be replaced with the newly postulated concept of “epistemologically different worlds” (EDWs). Consequently, we try to demonstrate that notions like “dark matter” and “dark energy” do not have a proper ontological basis: due to the correspondences between two EDWs, the macro-epistemological world (EW) (the EW of macro-entities like planets and tables) and the mega-EW or the macro– macro-EW (the EW of certain entities and processes that do not exist for the ED entities that belong to the macro-EW). Thus, we have to rethink the notions like “dark matter” and “dark energy” within the EDW perspective. We make an analogy with quantum mechanics: the “entanglement” is a process that belongs to the wave- EW, but not to the micro-EW (where those two microparticles are placed). The same principle works for explaining dark matter and dark energy: it is about entities and processes that belong to the “mega-EW,” but not to the macro-EW. The EDW perspective (2002, 2005, 2007, 2008) presupposes a new framework within which some general issues in physics should be addressed: (1) the dark matter, dark energy, and some other related issues from cosmology, (2) the main problems of quantum mechanics, (3) the relationship between Einstein’s general relativity and quantum mechanics, and so on.
    [Show full text]
  • General Neutralino NLSP with Gravitino Dark Matter Vs. Big Bang Nucleosynthesis
    General Neutralino NLSP with Gravitino Dark Matter vs. Big Bang Nucleosynthesis II. Institut fur¨ Theoretische Physik, Universit¨at Hamburg Deutsches Elektronen-Synchrotron DESY, Theory Group Diplomarbeit zur Erlangung des akademischen Grades Diplom-Physiker (diploma thesis - with correction) Verfasser: Jasper Hasenkamp Matrikelnummer: 5662889 Studienrichtung: Physik Eingereicht am: 31.3.2009 Betreuer(in): Dr. Laura Covi, DESY Zweitgutachter: Prof. Dr. Gun¨ ter Sigl, Universit¨at Hamburg ii Abstract We study the scenario of gravitino dark matter with a general neutralino being the next- to-lightest supersymmetric particle (NLSP). Therefore, we compute analytically all 2- and 3-body decays of the neutralino NLSP to determine the lifetime and the electro- magnetic and hadronic branching ratio of the neutralino decaying into the gravitino and Standard Model particles. We constrain the gravitino and neutralino NLSP mass via big bang nucleosynthesis and see how those bounds are relaxed for a Higgsino or a wino NLSP in comparison to the bino neutralino case. At neutralino masses & 1 TeV, a wino NLSP is favoured, since it decays rapidly via a newly found 4-vertex. The Higgsino component becomes important, when resonant annihilation via heavy Higgses can occur. We provide the full analytic results for the decay widths and the complete set of Feyn- man rules necessary for these computations. This thesis closes any gap in the study of gravitino dark matter scenarios with neutralino NLSP coming from approximations in the calculation of the neutralino decay rates and its hadronic branching ratio. Zusammenfassung Diese Diplomarbeit befasst sich mit dem Gravitino als Dunkler Materie, wobei ein allge- meines Neutralino das n¨achstleichteste supersymmetrische Teilchen (NLSP) ist.
    [Show full text]