DOCSLIB.ORG

Supersymmetric Particle Searches

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Supersymmetric Particle Searches Citation: K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014) (URL: http://pdg.lbl.gov) Supersymmetric Particle Searches A REVIEW GOES HERE – Check our WWW List of Reviews A REVIEW GOES HERE – Check our WWW List of Reviews SUPERSYMMETRIC MODEL ASSUMPTIONS The exclusion of particle masses within a mass range (m1, m2) will be denoted with the notation “none m m ” in the VALUE column of the 1− 2 following Listings. The latest unpublished results are described in the “Supersymmetry: Experiment” review. A REVIEW GOES HERE – Check our WWW List of Reviews CONTENTS: χ0 (Lightest Neutralino) Mass Limit 1 e Accelerator limits for stable χ0 − 1 Bounds on χ0 from dark mattere searches − 1 χ0-p elastice cross section − 1 eSpin-dependent interactions Spin-independent interactions Other bounds on χ0 from astrophysics and cosmology − 1 Unstable χ0 (Lighteste Neutralino) Mass Limit − 1 χ0, χ0, χ0 (Neutralinos)e Mass Limits 2 3 4 χe ,eχ e(Charginos) Mass Limits 1± 2± Long-livede e χ± (Chargino) Mass Limits ν (Sneutrino)e Mass Limit Chargede Sleptons e (Selectron) Mass Limit − µ (Smuon) Mass Limit − e τ (Stau) Mass Limit − e Degenerate Charged Sleptons − e ℓ (Slepton) Mass Limit − q (Squark)e Mass Limit Long-livede q (Squark) Mass Limit b (Sbottom)e Mass Limit te (Stop) Mass Limit eHeavy g (Gluino) Mass Limit Long-lived/lighte g (Gluino) Mass Limit Light G (Gravitino)e Mass Limits from Collider Experiments Supersymmetrye Miscellaneous Results HTTP://PDG.LBL.GOV Page1 Created: 8/21/2014 12:57 Citation: K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014) (URL: http://pdg.lbl.gov) 0 χ1 (Lightest Neutralino) MASS LIMIT χ0 is often assumed to be the lightest supersymmetric particle (LSP). See also the e 1 χe0, χ0, χ0 section below. 2 3 4 e e e We have divided the χ0 listings below into five sections: 1 e 1) Accelerator limits for stable χ0, 1 2) Bounds on χ0 from dark mattere searches, 1 3) χ0 p elastice cross section (spin-dependent, spin-independent interactions), 1 − e 0 4) Other bounds on χ1 from astrophysics and cosmology, and 5) Unstable χ0 (Lighteste Neutralino) mass limit. 1 e 0 Accelerator limits for stable χ1 Unless otherwise stated, results in this section assumee spectra, production rates, decay modes, and branching ratios as evaluated in the MSSM, with gaugino and sfermion mass unification at the GUT scale. These papers generally study production of χ0 χ0 (i 1, j 2), χ+ χ , and (in the i j ≥ ≥ 1 1− case of hadronic collisions) χ+eχ0epairs. The mass limitse e on χ0 are either 1 2 1 direct, or follow indirectly frome e the constraints set by the non-observatione of χ and χ0 states on the gaugino and higgsino MSSM parameters M 1± 2 2 ande µ. Ine some cases, information is used from the nonobservation of slepton decays. + Obsolete limits obtained from e e− collisions up to √s=184 GeV have been removed from this compilation and can be found in the 2000 Edi- tion (The European Physical Journal C15 1 (2000)) of this Review. ∆m=m 0 m 0 . χ2 − χ1 e e VALUE (GeV) CL% DOCUMENT ID TECN COMMENT >40 95 1 ABBIENDI 04H OPAL all tanβ, ∆m >5 GeV, m0 >500 GeV, A0 = 0 2 >42.4 95 HEISTER 04 ALEP alltanβ, all ∆m, all m0 3 >39.2 95 ABDALLAH 03M DLPH all tanβ, mν >500 GeV 4 >46 95 ABDALLAH 03M DLPH all tanβ, all ∆m, all m0 5 e >32.5 95 ACCIARRI 00D L3 tanβ > 0.7, ∆m > 3 GeV, all m0 We do not use the following data for averages, fits, limits, etc. ••• ••• 6 DREINER 09 THEO 1 ABBIENDI 04H search for charginos and neutralinos in events with acoplanar leptons+jets and multi-jet final states in the 192–209 GeV data, combined with the results on leptonic final states from ABBIENDI 04. The results hold for a scan over the parameter space covering the region 0 < M2 <5000 GeV, 1000 <µ<1000 GeV and tanβ from 1 to 40. This limit supersedes ABBIENDI 00H. − 2 HEISTER 04 data collected up to 209 GeV. Updates earlier analysis of selectrons from HEISTER 02E, includes a new analysis of charginos and neutralinos decaying into stau and uses results on charginos with initial state radiation from HEISTER 02J. The limit is based on the direct search for charginos and neutralinos, the constraints from the slepton search and the Higgs mass limits from HEISTER 02 using a top mass of 175 GeV, interpreted in a framework with universal gaugino and sfermion masses. Assuming the mixing in the stau sector to be negligible, the limit improves to 43.1GeV. Under the HTTP://PDG.LBL.GOV Page2 Created: 8/21/2014 12:57 Citation: K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014) (URL: http://pdg.lbl.gov) assumption of MSUGRA with unification of the Higgs and sfermion masses, the limit improves to 50GeV, and reaches 53GeV for A0 = 0. These limits include and update the results of BARATE 01. 3 ABDALLAH 03M uses data from √s = 192–208 GeV. A limit on the mass of χ0 is derived 1 from direct searches for neutralinos combined with the chargino search. Neutralinose are searched in the production of χ0χ0, χ0χ0, as well as χ0χ0 and χ0χ0 giving rise to 1 2 1 3 2 3 2 4 cascade decays, and χ0χ0 ande χe0χ0,e followede by the decaye e χ0 e eτ τ. The results 1 2 1 2 2 → hold for the parametere spacee definede e by values of M < 1 TeV,e µ e2 TeV with the 2 ¯ ¯ ≤ χ0 as LSP. The limit is obtained for tanβ = 1 and large m , where¯ ¯χ0χ0 and chargino 1 0 2 4 paire production are important. If the constraint from Higgs searchese e is also imposed, max the limit improves to 49.0 GeV in the mh scenario with mt=174.3 GeV. These limits update the results of ABREU 00J. 4 ABDALLAH 03M uses data from √s = 192–208 GeV. An indirect limit on the mass of χ0 is derived by constraining the MSSM parameter space by the results from direct 1 searchese for neutralinos (including cascade decays and ττ final states), for charginos (for all ∆m+) and for sleptons, stop and sbottom. The resultse hold for the full parameter space defined by values of M < 1 TeV, µ 2TeV with the χ0 as LSP. Constraints 2 ¯ ¯ ≤ 1 max ¯ ¯ e from the Higgs search in the mh scenario assuming mt =174.3 GeV are included. The limit is obtained for tanβ 5 when stau mixing leads to mass degeneracy between τ ≥ 1 and χ0 and the limit is based on χ0 production followed by its decay to τ τ. In the 1 2 1 e pathologicale scenario where m andeµ are large, so that the χ0 production crosse section 0 ¯ ¯ 2 is negligible, and where there is mixing¯ ¯ in the stau sector buet not in stop nor sbottom, the limit is based on charginos with soft decay products and an ISR photon. The limit then degrades to 39 GeV. See Figs 40–42 for the dependence of the limit on tanβ and mν . These limits update the results of ABREU 00W. 5 ACCIARRIe 00D data collected at √s=189 GeV. The results hold over the full parameter space defined by 0.7 tanβ 60, 0 M 2 TeV, m 500 GeV, µ 2 TeV ≤ ≤ ≤ 2 ≤ 0 ≤ ¯ ¯ ≤ The minimum mass limit is reached for tanβ=1 and large m0. The results¯ ¯ of slepton searches from ACCIARRI 99W are used to help set constraints in the region of small m0. > > The limit improves to 48 GeV for m0 200 GeV and tanβ 10. See their Figs. 6–8 for the tanβ and m0 dependence of the limits.∼ Updates ACCIARRI∼ 98F. 6 DREINER 09 show that in the general MSSM with non-universal gaugino masses there exists no model-independent laboratory bound on the mass of the lightest neutralino. An essentially massless χ0 is allowed by the experimental and observational data, imposing 1 some constraints on other MSSM parameters, including M2, µ and the slepton and squark masses. 0 Bounds on χ1 from dark matter searches e These papers generally excludee regions in the M2 – µ parameter plane assuming that χ0 is the dominant form of dark matter in the galactic halo. 1 These limits aree based on the lack of detection in laboratory experiments, telescopes, or by the absence of a signal in underground neutrino detectors. The latter signal is expected if χ0 accumulates in the Sun or the Earth 1 and annihilates into high-energy eν’s. VALUE DOCUMENT ID TECN We do not use the following data for averages, fits, limits, etc. ••• ••• 1 AARTSEN 13 ICCB 2 AARTSEN 13C ICCB 3 ABRAMOWSKI13 HESS HTTP://PDG.LBL.GOV Page3 Created: 8/21/2014 12:57 Citation: K.A. Olive et al. (Particle Data Group), Chin. Phys. C38, 090001 (2014) (URL: http://pdg.lbl.gov) 4 ACKERMANN 13A FRMI 5 ADRIAN-MAR...13 ANTR 6 BERGSTROM 13 COSM 7 BOLIEV 13 BAKS 6 JIN 13 ASTR 6 KOPP 13 COSM 8 ABBASI 12 ICCB 9 ABRAMOWSKI11 HESS 10 ABDO 10 FRMI 11 ACKERMANN 10 FRMI 12 ABBASI 09B ICCB 13 ACHTERBERG 06 AMND 14 ACKERMANN 06 AMND 15 DEBOER 06 RVUE 16 DESAI 04 SKAM 16 AMBROSIO 99 MCRO 17 LOSECCO 95 RVUE 18 MORI 93 KAMI 19 BOTTINO 92 COSM 20 BOTTINO 91 RVUE 21 GELMINI 91 COSM 22 KAMIONKOW...91 RVUE 23 MORI 91B KAMI none 4–15 GeV 24 OLIVE 88 COSM 1 AARTSEN 13 is based on data collected during 317 effective days with the IceCube 79- string detector including the DeepCore sub-array.
Load more

Recommended publications
  • Constraints from Electric Dipole Moments on Chargino Baryogenesis in the Minimal Supersymmetric Standard Model
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by National Tsing Hua University Institutional Repository PHYSICAL REVIEW D 66, 116008 ͑2002͒ Constraints from electric dipole moments on chargino baryogenesis in the minimal supersymmetric standard model Darwin Chang NCTS and Physics Department, National Tsing-Hua University, Hsinchu 30043, Taiwan, Republic of China and Theory Group, Lawrence Berkeley Lab, Berkeley, California 94720 We-Fu Chang NCTS and Physics Department, National Tsing-Hua University, Hsinchu 30043, Taiwan, Republic of China and TRIUMF Theory Group, Vancouver, British Columbia, Canada V6T 2A3 Wai-Yee Keung NCTS and Physics Department, National Tsing-Hua University, Hsinchu 30043, Taiwan, Republic of China and Physics Department, University of Illinois at Chicago, Chicago, Illinois 60607-7059 ͑Received 9 May 2002; revised 13 September 2002; published 27 December 2002͒ A commonly accepted mechanism of generating baryon asymmetry in the minimal supersymmetric standard model ͑MSSM͒ depends on the CP violating relative phase between the gaugino mass and the Higgsino ␮ term. The direct constraint on this phase comes from the limit of electric dipole moments ͑EDM’s͒ of various light fermions. To avoid such a constraint, a scheme which assumes that the first two generation sfermions are very heavy is usually evoked to suppress the one-loop EDM contributions. We point out that under such a scheme the most severe constraint may come from a new contribution to the electric dipole moment of the electron, the neutron, or atoms via the chargino sector at the two-loop level. As a result, the allowed parameter space for baryogenesis in the MSSM is severely constrained, independent of the masses of the first two generation sfermions.
    [Show full text]
  • The Pev-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability
    The PeV-Scale Split Supersymmetry from Higgs Mass and Electroweak Vacuum Stability Waqas Ahmed ? 1, Adeel Mansha ? 2, Tianjun Li ? ~ 3, Shabbar Raza ∗ 4, Joydeep Roy ? 5, Fang-Zhou Xu ? 6, ? CAS Key Laboratory of Theoretical Physics, Institute of Theoretical Physics, Chinese Academy of Sciences, Beijing 100190, P. R. China ~School of Physical Sciences, University of Chinese Academy of Sciences, No. 19A Yuquan Road, Beijing 100049, P. R. China ∗ Department of Physics, Federal Urdu University of Arts, Science and Technology, Karachi 75300, Pakistan Institute of Modern Physics, Tsinghua University, Beijing 100084, China Abstract The null results of the LHC searches have put strong bounds on new physics scenario such as supersymmetry (SUSY). With the latest values of top quark mass and strong coupling, we study the upper bounds on the sfermion masses in Split-SUSY from the observed Higgs boson mass and electroweak (EW) vacuum stability. To be consistent with the observed Higgs mass, we find that the largest value of supersymmetry breaking 3 1:5 scales MS for tan β = 2 and tan β = 4 are O(10 TeV) and O(10 TeV) respectively, thus putting an upper bound on the sfermion masses around 103 TeV. In addition, the Higgs quartic coupling becomes negative at much lower scale than the Standard Model (SM), and we extract the upper bound of O(104 TeV) on the sfermion masses from EW vacuum stability. Therefore, we obtain the PeV-Scale Split-SUSY. The key point is the extra contributions to the Renormalization Group Equation (RGE) running from arXiv:1901.05278v1 [hep-ph] 16 Jan 2019 the couplings among Higgs boson, Higgsinos, and gauginos.
    [Show full text]
  • Table of Contents (Print)
    PERIODICALS PHYSICAL REVIEW D Postmaster send address changes to: For editorial and subscription correspondence, PHYSICAL REVIEW D please see inside front cover APS Subscription Services „ISSN: 0556-2821… Suite 1NO1 2 Huntington Quadrangle Melville, NY 11747-4502 THIRD SERIES, VOLUME 69, NUMBER 7 CONTENTS D1 APRIL 2004 RAPID COMMUNICATIONS ϩ 0 ⌼ ϩ→ ␺ ϩ 0→ ␺ 0 Measurement of the B /B production ratio from the (4S) meson using B J/ K and B J/ KS decays (7 pages) ............................................................................ 071101͑R͒ B. Aubert et al. ͑BABAR Collaboration͒ Cabibbo-suppressed decays of Dϩ→␲ϩ␲0,KϩK¯ 0,Kϩ␲0 (5 pages) .................................. 071102͑R͒ K. Arms et al. ͑CLEO Collaboration͒ Ϯ→␹ Ϯ ͑ ͒ Measurement of the branching fraction for B c0K (7 pages) ................................... 071103R B. Aubert et al. ͑BABAR Collaboration͒ Generalized Ward identity and gauge invariance of the color-superconducting gap (5 pages) .............. 071501͑R͒ De-fu Hou, Qun Wang, and Dirk H. Rischke ARTICLES Measurements of ␺(2S) decays into vector-tensor final states (6 pages) ............................... 072001 J. Z. Bai et al. ͑BES Collaboration͒ Measurement of inclusive momentum spectra and multiplicity distributions of charged particles at ͱsϳ2 –5 GeV (7 pages) ................................................................... 072002 J. Z. Bai et al. ͑BES Collaboration͒ Production of ␲ϩ, ␲Ϫ, Kϩ, KϪ, p, and ¯p in light ͑uds͒, c, and b jets from Z0 decays (26 pages) ........ 072003 Koya Abe et al. ͑SLD Collaboration͒ Heavy flavor properties of jets produced in pp¯ interactions at ͱsϭ1.8 TeV (21 pages) .................. 072004 D. Acosta et al. ͑CDF Collaboration͒ Electric charge and magnetic moment of a massive neutrino (21 pages) ............................... 073001 Maxim Dvornikov and Alexander Studenikin ␶→␲␲␲␯␶ decays in the resonance effective theory (13 pages) ....................................
    [Show full text]
  • 1 Standard Model: Successes and Problems
    Searching for new particles at the Large Hadron Collider James Hirschauer (Fermi National Accelerator Laboratory) Sambamurti Memorial Lecture : August 7, 2017 Our current theory of the most fundamental laws of physics, known as the standard model (SM), works very well to explain many aspects of nature. Most recently, the Higgs boson, predicted to exist in the late 1960s, was discovered by the CMS and ATLAS collaborations at the Large Hadron Collider at CERN in 2012 [1] marking the first observation of the full spectrum of predicted SM particles. Despite the great success of this theory, there are several aspects of nature for which the SM description is completely lacking or unsatisfactory, including the identity of the astronomically observed dark matter and the mass of newly discovered Higgs boson. These and other apparent limitations of the SM motivate the search for new phenomena beyond the SM either directly at the LHC or indirectly with lower energy, high precision experiments. In these proceedings, the successes and some of the shortcomings of the SM are described, followed by a description of the methods and status of the search for new phenomena at the LHC, with some focus on supersymmetry (SUSY) [2], a specific theory of physics beyond the standard model (BSM). 1 Standard model: successes and problems The standard model of particle physics describes the interactions of fundamental matter particles (quarks and leptons) via the fundamental forces (mediated by the force carrying particles: the photon, gluon, and weak bosons). The Higgs boson, also a fundamental SM particle, plays a central role in the mechanism that determines the masses of the photon and weak bosons, as well as the rest of the standard model particles.
    [Show full text]
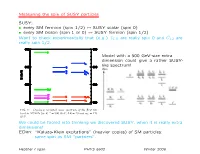
  • Measuring the Spin of SUSY Particles SUSY: • Every SM Fermion (Spin 1/2
    Measuring the spin of SUSY particles SUSY: • every SM fermion (spin 1/2) ↔ SUSY scalar (spin 0) • every SM boson (spin 1 or 0) ↔ SUSY fermion (spin 1/2) Want to check experimentally that (e.g.) eL,R are really spin 0 and Ce1,2 are really spin 1/2. 2 preserve the 5th dimensional momentum (KK number). The corresponding coupling constants among KK modes Model with a 500 GeV-size extra are simply equal to the SM couplings (up to normaliza- tion factors such as √2). The Feynman rules for the KK dimension could give a rather SUSY- modes can easily be derived (e.g., see Ref. [8, 9]). like spectrum! In contrast, the coefficients of the boundary terms are not fixed by Standard Model couplings and correspond to new free parameters. In fact, they are renormalized by the bulk interactions and hence are scale dependent [10, 11]. One might worry that this implies that all pre- dictive power is lost. However, since the wave functions of Standard Model fields and KK modes are spread out over the extra dimension and the new couplings only exist on the boundaries, their effects are volume sup- pressed. We can get an estimate for the size of these volume suppressed corrections with naive dimensional analysis by assuming strong coupling at the cut-off. The FIG. 1: One-loop corrected mass spectrum of the first KK −1 result is that the mass shifts to KK modes from bound- level in MUEDs for R = 500 GeV, ΛR = 20 and mh = 120 ary terms are numerically equal to corrections from loops GeV.
    [Show full text]
  • Study of $ S\To D\Nu\Bar {\Nu} $ Rare Hyperon Decays Within the Standard
    Study of s dνν¯ rare hyperon decays in the Standard Model and new physics → Xiao-Hui Hu1 ∗, Zhen-Xing Zhao1 † 1 INPAC, Shanghai Key Laboratory for Particle Physics and Cosmology, MOE Key Laboratory for Particle Physics, Astrophysics and Cosmology, School of Physics and Astronomy, Shanghai Jiao-Tong University, Shanghai 200240, P.R. China FCNC processes offer important tools to test the Standard Model (SM), and to search for possible new physics. In this work, we investigate the s → dνν¯ rare hyperon decays in SM and beyond. We 14 11 find that in SM the branching ratios for these rare hyperon decays range from 10− to 10− . When all the errors in the form factors are included, we find that the final branching fractions for most decay modes have an uncertainty of about 5% to 10%. After taking into account the contribution from new physics, the generalized SUSY extension of SM and the minimal 331 model, the decay widths for these channels can be enhanced by a factor of 2 ∼ 7. I. INTRODUCTION The flavor changing neutral current (FCNC) transitions provide a critical test of the Cabibbo-Kobayashi-Maskawa (CKM) mechanism in the Standard Model (SM), and allow to search for the possible new physics. In SM, FCNC transition s dνν¯ proceeds through Z-penguin and electroweak box diagrams, and thus the decay probablitities are strongly→ suppressed. In this case, a precise study allows to perform very stringent tests of SM and ensures large sensitivity to potential new degrees of freedom. + + 0 A large number of studies have been performed of the K π νν¯ and KL π νν¯ processes, and reviews of these two decays can be found in [1–6].
    [Show full text]
  • Thesissubmittedtothe Florida State University Department of Physics in Partial Fulfillment of the Requirements for Graduation with Honors in the Major
    Florida State University Libraries 2016 Search for Electroweak Production of Supersymmetric Particles with two photons, an electron, and missing transverse energy Paul Myles Eugenio Follow this and additional works at the FSU Digital Library. For more information, please contact [email protected] ASEARCHFORELECTROWEAK PRODUCTION OF SUPERSYMMETRIC PARTICLES WITH TWO PHOTONS, AN ELECTRON, AND MISSING TRANSVERSE ENERGY Paul Eugenio Athesissubmittedtothe Florida State University Department of Physics in partial fulfillment of the requirements for graduation with Honors in the Major Spring 2016 2 Abstract A search for Supersymmetry (SUSY) using a final state consisting of two pho- tons, an electron, and missing transverse energy. This analysis uses data collected by the Compact Muon Solenoid (CMS) detector from proton-proton collisions at a center of mass energy √s =13 TeV. The data correspond to an integrated luminosity of 2.26 fb−1. This search focuses on a R-parity conserving model of Supersymmetry where electroweak decay of SUSY particles results in the lightest supersymmetric particle, two high energy photons, and an electron. The light- est supersymmetric particle would escape the detector, thus resulting in missing transverse energy. No excess of missing energy is observed in the signal region of MET>100 GeV. A limit is set on the SUSY electroweak Chargino-Neutralino production cross section. 3 Contents 1 Introduction 9 1.1 Weakly Interacting Massive Particles . ..... 10 1.2 SUSY ..................................... 12 2 CMS Detector 15 3Data 17 3.1 ParticleFlowandReconstruction . .. 17 3.1.1 ECALClusteringandR9. 17 3.1.2 Conversion Safe Electron Veto . 18 3.1.3 Shower Shape . 19 3.1.4 Isolation .
    [Show full text]
  • Jhep11(2016)148
    Published for SISSA by Springer Received: August 9, 2016 Revised: October 28, 2016 Accepted: November 20, 2016 Published: November 24, 2016 JHEP11(2016)148 Split NMSSM with electroweak baryogenesis S.V. Demidov,a;b D.S. Gorbunova;b and D.V. Kirpichnikova aInstitute for Nuclear Research of the Russian Academy of Sciences, 60th October Anniversary prospect 7a, Moscow 117312, Russia bMoscow Institute of Physics and Technology, Institutsky per. 9, Dolgoprudny 141700, Russia E-mail: [email protected], [email protected], [email protected] Abstract: In light of the Higgs boson discovery and other results of the LHC we re- consider generation of the baryon asymmetry in the split Supersymmetry model with an additional singlet superfield in the Higgs sector (non-minimal split SUSY). We find that successful baryogenesis during the first order electroweak phase transition is possible within a phenomenologically viable part of the model parameter space. We discuss several phenomenological consequences of this scenario, namely, predictions for the electric dipole moments of electron and neutron and collider signatures of light charginos and neutralinos. Keywords: Supersymmetry Phenomenology ArXiv ePrint: 1608.01985 Open Access, c The Authors. doi:10.1007/JHEP11(2016)148 Article funded by SCOAP3. Contents 1 Introduction1 2 Non-minimal split supersymmetry3 3 Predictions for the Higgs boson mass5 4 Strong first order EWPT8 JHEP11(2016)148 5 Baryon asymmetry9 6 EDM constraints and light chargino phenomenology 12 7 Conclusion 13 A One loop corrections to Higgs mass in split NMSSM 14 A.1 Tree level potential of scalar sector in the broken phase 14 A.2 Chargino-neutralino sector of split NMSSM 16 A.3 One-loop correction to Yukawa coupling of top quark 17 1 Introduction Any phenomenologically viable particle physics model should explain the observed asym- metry between matter and antimatter in the Universe.
    [Show full text]
  • Electroweak Radiative B-Decays As a Test of the Standard Model and Beyond Andrey Tayduganov
    Electroweak radiative B-decays as a test of the Standard Model and beyond Andrey Tayduganov To cite this version: Andrey Tayduganov. Electroweak radiative B-decays as a test of the Standard Model and beyond. Other [cond-mat.other]. Université Paris Sud - Paris XI, 2011. English. NNT : 2011PA112195. tel-00648217 HAL Id: tel-00648217 https://tel.archives-ouvertes.fr/tel-00648217 Submitted on 5 Dec 2011 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. LAL 11-181 LPT 11-69 THESE` DE DOCTORAT Pr´esent´eepour obtenir le grade de Docteur `esSciences de l’Universit´eParis-Sud 11 Sp´ecialit´e:PHYSIQUE THEORIQUE´ par Andrey Tayduganov D´esint´egrationsradiatives faibles de m´esons B comme un test du Mod`eleStandard et au-del`a Electroweak radiative B-decays as a test of the Standard Model and beyond Soutenue le 5 octobre 2011 devant le jury compos´ede: Dr. J. Charles Examinateur Prof. A. Deandrea Rapporteur Prof. U. Ellwanger Pr´esident du jury Prof. S. Fajfer Examinateur Prof. T. Gershon Rapporteur Dr. E. Kou Directeur de th`ese Dr. A. Le Yaouanc Directeur de th`ese Dr.
    [Show full text]
  • Mass Degeneracy of the Higgsinos
    CERN–TH/95–337 Mass Degeneracy of the Higgsinos Gian F. Giudice1 and Alex Pomarol Theory Division, CERN CH-1211 Geneva 23, Switzerland Abstract The search for charginos and neutralinos at LEP2 can become problematic if these particles are almost mass degenerate with the lightest neutralino. Unfortunately this is the case in the region where these particles are higgsino-like. We show that, in this region, radiative corrections to the higgsino mass splittings can be as large as the tree-level values, if the mixing between the two stop states is large. We also show that the degree of degeneracy of the higgsinos substantially increases if a large phase is present in the higgsino mass term µ. CERN–TH/95–337 December 1995 1On leave of absence from INFN Sezione di Padova, Padua, Italy. The search for charginos (˜χ+) at LEP2 is one of the most promising ways of discovering low-energy supersymmetry. If theχ ˜+ decays into the lightest neutralino (˜χ0) and a virtual W +, it can be discovered at LEP2 (with a L = 500 pb−1) whenever its production cross R section is larger than about 0.1–0.3pbandmχ˜0 is within the range mχ˜0 ∼> 20 GeV and mχ˜+ − mχ˜0 ∼> 5–10 GeV [1]. Therefore, the chargino can be discovered almost up to the LEP2 kinematical limit, unless one of the following three conditions occurs: i) The sneutrino (˜ν) is light and the chargino is mainly gaugino-like. In this case theν ˜ t-channel exchange interferes destructively with the gauge-boson exchange and can reduce the chargino production cross section below the minimum values required for observability, 0.1–0.3 pb.
    [Show full text]
  • The Minimal Supersymmetric Standard Model: Group Summary Report
    PM/98–45 December 1998 The Minimal Supersymmetric Standard Model: Group Summary Report Conveners: A. Djouadi1, S. Rosier-Lees2 Working Group: M. Bezouh1, M.-A. Bizouard3,C.Boehm1, F. Borzumati1;4,C.Briot2, J. Carr5,M.B.Causse6, F. Charles7,X.Chereau2,P.Colas8, L. Duflot3, A. Dupperin9, A. Ealet5, H. El-Mamouni9, N. Ghodbane9, F. Gieres9, B. Gonzalez-Pineiro10, S. Gourmelen9, G. Grenier9, Ph. Gris8, J.-F. Grivaz3,C.Hebrard6,B.Ille9, J.-L. Kneur1, N. Kostantinidis5, J. Layssac1,P.Lebrun9,R.Ledu11, M.-C. Lemaire8, Ch. LeMouel1, L. Lugnier9 Y. Mambrini1, J.P. Martin9,G.Montarou6,G.Moultaka1, S. Muanza9,E.Nuss1, E. Perez8,F.M.Renard1, D. Reynaud1,L.Serin3, C. Thevenet9, A. Trabelsi8,F.Zach9,and D. Zerwas3. 1 LPMT, Universit´e Montpellier II, F{34095 Montpellier Cedex 5. 2 LAPP, BP 110, F{74941 Annecy le Vieux Cedex. 3 LAL, Universit´e de Paris{Sud, Bat{200, F{91405 Orsay Cedex 4 CERN, Theory Division, CH{1211, Geneva, Switzerland. 5 CPPM, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. 6 LPC Clermont, Universit´e Blaise Pascal, F{63177 Aubiere Cedex. 7 GRPHE, Universit´e de Haute Alsace, Mulhouse 8 SPP, CEA{Saclay, F{91191 Cedex 9 IPNL, Universit´e Claude Bernard de Lyon, F{69622 Villeurbanne Cedex. 10 LPNHE, Universit´es Paris VI et VII, Paris Cedex. 11 CPT, Universit´e de Marseille-Luminy, Case 907, F-13288 Marseille Cedex 9. Report of the MSSM working group for the Workshop \GDR{Supersym´etrie". 1 CONTENTS 1. Synopsis 4 2. The MSSM Spectrum 9 2.1 The MSSM: Definitions and Properties 2.1.1 The uMSSM: unconstrained MSSM 2.1.2 The pMSSM: “phenomenological” MSSM 2.1.3 mSUGRA: the constrained MSSM 2.1.4 The MSSMi: the intermediate MSSMs 2.2 Electroweak Symmetry Breaking 2.2.1 General features 2.2.2 EWSB and model–independent tanβ bounds 2.3 Renormalization Group Evolution 2.3.1 The one–loop RGEs 2.3.2 Exact solutions for the Yukawa coupling RGEs 3.
    [Show full text]
  • Table of Contents (Print)
    PERIODICALS PHYSICAL REVIEW D Postmaster send address changes to: For editorial and subscription correspondence, American Institute of Physics please see inside front cover 500 Sunnyside Boulevard (ISSN: 0556-2821) Woodbury, NY 11797-2999 THIRD SERIES, VOLUME 55, NUMBER 3 CONTENTS 1 FEBRUARY 1997 RAPID COMMUNICATIONS Search for f mesons in t lepton decay ............................................................. R1119 P. Avery et al. ~CLEO Collaboration! Is factorization for isolated photon cross sections broken? .............................................. R1124 P. Aurenche, M. Fontannaz, J. Ph. Guillet, A. Kotikov, and E. Pilon Long distance contribution to D pl1l2 ........................................................... R1127 Paul Singer and Da-Xin Zhang→ Forward scattering amplitude of virtual longitudinal photons at zero energy ............................... R1130 B. L. Ioffe Improving flavor symmetry in the Kogut-Susskind hadron spectrum ...................................... R1133 Tom Blum, Carleton DeTar, Steven Gottlieb, Kari Rummukainen, Urs M. Heller, James E. Hetrick, Doug Toussaint, R. L. Sugar, and Matthew Wingate Anomalous U~1!-mediated supersymmetry breaking, fermion masses, and natural suppression of FCNC and CP-violating effects ............................................................................. R1138 R. N. Mohapatra and Antonio Riotto ARTICLES 0 Observation of L b J/c L at the Fermilab proton-antiproton collider .................................... 1142 F. Abe et al.→~CDF Collaboration! Measurement of the branching ratios c8 e1e2, c8 J/cpp, and c8 J/ch ............................ 1153 T. A. Armstrong et al. ~Fermilab→ E760 Collaboration→ ! → Measurement of the differences in the total cross section for antiparallel and parallel longitudinal spins and a measurement of parity nonconservation with incident polarized protons and antiprotons at 200 GeV/c .......... 1159 D. P. Grosnick et al. ~E581/704 Collaboration! Statistical properties of the linear s model used in dynamical simulations of DCC formation ................
    [Show full text]