DOCSLIB.ORG

Chapter Two Vector Spaces

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Chapter Two Vector Spaces Chapter Two Vector Spaces The first chapter began by introducing Gauss’ method and finished with a fair understanding, keyed on the Linear Combination Lemma, of how it finds the solution set of a linear system. Gauss’ method systematically takes linear com- binations of the rows. With that insight, we now move to a general study of linear combinations. We need a setting for this study. At times in the first chapter, we’ve com- bined vectors from R2, at other times vectors from R3, and at other times vectors from even higher-dimensional spaces. Thus, our first impulse might be to work in Rn, leaving n unspecified. This would have the advantage that any of the results would hold for R2 and for R3 and for many other spaces, simultaneously. But, if having the results apply to many spaces at once is advantageous then sticking only to Rn’s is overly restrictive. We’d like the results to also apply to combinations of row vectors, as in the final section of the first chapter. We’ve even seen some spaces that are not just a collection of all of the same-sized column vectors or row vectors. For instance, we’ve seen a solution set of a homogeneous system that is a plane, inside of R3. This solution set is a closed system in the sense that a linear combination of these solutions is also a solution. But it is not just a collection of all of the three-tall column vectors; only some of them are in this solution set. We want the results about linear combinations to apply anywhere that linear combinations are sensible. We shall call any such set a vector space. Our results, instead of being phrased as “Whenever we have a collection in which we can sensibly take linear combinations . ”, will be stated as “In any vector space . ”. Such a statement describes at once what happens in many spaces. The step up in abstraction from studying a single space at a time to studying a class of spaces can be hard to make. To understand its advantages, consider this analogy. Imagine that the government made laws one person at a time: “Leslie Jones can’t jay walk.” That would be a bad idea; statements have the virtue of economy when they apply to many cases at once. Or, suppose that they ruled, “Kim Ke must stop when passing the scene of an accident.” Contrast that with, “Any doctor must stop when passing the scene of an accident.” More general statements, in some ways, are clearer. 79 80 Chapter Two. Vector Spaces I Definition of Vector Space We shall study structures with two operations, an addition and a scalar multi- plication, that are subject to some simple conditions. We will reflect more on the conditions later, but on first reading notice how reasonable they are. For instance, surely any operation that can be called an addition (e.g., column vec- tor addition, row vector addition, or real number addition) will satisfy all the conditions in (1) below. I.1 Definition and Examples 1.1 Definition A vector space (over R) consists of a set V along with two operations ‘+’ and ‘¢’ such that (1) if ~v; ~w 2 V then their vector sum ~v + ~w is in V and ² ~v + ~w = ~w + ~v ² (~v + ~w) + ~u = ~v + (~w + ~u) (where ~u 2 V ) ² there is a zero vector ~0 2 V such that ~v + ~0 = ~v for all ~v 2 V ² each ~v 2 V has an additive inverse ~w 2 V such that ~w + ~v = ~0 (2) if r; s are scalars (members of R) and ~v; ~w 2 V then each scalar multiple r ¢ ~v is in V and ² (r + s) ¢ ~v = r ¢ ~v + s ¢ ~v ² r ¢ (~v + ~w) = r ¢ ~v + r ¢ ~w ² (rs) ¢ ~v = r ¢ (s ¢ ~v) ² 1 ¢ ~v = ~v. 1.2 Remark Because it involves two kinds of addition and two kinds of mul- tiplication, that definition may seem confused. For instance, in ‘(r + s) ¢ ~v = r ¢ ~v + s ¢ ~v ’, the first ‘+’ is the real number addition operator while the ‘+’ to the right of the equals sign represents vector addition in the structure V . These expressions aren’t ambiguous because, e.g., r and s are real numbers so ‘r + s’ can only mean real number addition. The best way to go through the examples below is to check all of the con- ditions in the definition. That check is written out in the first example. Use it as a model for the others. Especially important are the two: ‘~v + ~w is in V ’ and ‘r ¢ ~v is in V ’. These are the closure conditions. They specify that the addition and scalar multiplication operations are always sensible — they must be defined for every pair of vectors, and every scalar and vector, and the result of the operation must be a member of the set (see Example 1.4). Edited by Foxit PDF Editor Copyright (c) by Foxit Software Company, 2004 For Evaluation Only. Section I. Definition of Vector Space 81 1.3 Example The set R2 is a vector space if the operations ‘+’ and ‘¢’ have their usual meaning. µ ¶ µ ¶ µ ¶ µ ¶ µ ¶ x y x + y x rx 1 + 1 = 1 1 r ¢ 1 = 1 x2 y2 x2 + y2 x2 rx2 We shall check all of the conditions in the definition. There are five conditions in item (1). First, for closure of addition, note that for any v1; v2; w1; w2 2 R the result of the sum µ ¶ µ ¶ µ ¶ v w v + w 1 + 1 = 1 1 v2 w2 v2 + w2 is a column array with two real entries, and so is in R2. Second, to show that addition of vectors commutes, take all entries to be real numbers and compute µ ¶ µ ¶ µ ¶ µ ¶ µ ¶ µ ¶ v w v + w w + v w v 1 + 1 = 1 1 = 1 1 = 1 + 1 v2 w2 v2 + w2 w2 + v2 w2 v2 (the second equality follows from the fact that the components of the vectors are real numbers, and the addition of real numbers is commutative). The third condition, associativity of vector addition, is similar. µ ¶ µ ¶ µ ¶ µ ¶ v w u (v + w ) + u ( 1 + 1 ) + 1 = 1 1 1 v2 w2 u2 (v2 + w2) + u2 µ ¶ v + (w + u ) = 1 1 1 v2 + (w2 + u2) µ ¶ µ ¶ µ ¶ v w u = 1 + ( 1 + 1 ) v2 w2 u2 For the fourth we must produce a zero element — the vector of zeroes is it. µ ¶ µ ¶ µ ¶ v 0 v 1 + = 1 v2 0 v2 Fifth, to produce an additive inverse, note that for any v1; v2 2 R we have µ ¶ µ ¶ µ ¶ ¡v v 0 1 + 1 = ¡v2 v2 0 so the first vector is the desired additive inverse of the second. The checks for the five conditions in item (2) are just as routine. First, for closure under scalar multiplication, where r; v1; v2 2 R, µ ¶ µ ¶ v rv r ¢ 1 = 1 v2 rv2 is a column array with two real entries, and so is in R2. This checks the second condition. µ ¶ µ ¶ µ ¶ µ ¶ µ ¶ v (r + s)v rv + sv v v (r + s) ¢ 1 = 1 = 1 1 = r ¢ 1 + s ¢ 1 v2 (r + s)v2 rv2 + sv2 v2 v2 Edited by Foxit PDF Editor Copyright (c) by Foxit Software Company, 2004 For Evaluation Only. 82 Chapter Two. Vector Spaces For the third condition, that scalar multiplication distributes from the left over vector addition, the check is also straightforward. µ ¶ µ ¶ µ ¶ µ ¶ µ ¶ µ ¶ v w r(v + w ) rv + rw v w r ¢ ( 1 + 1 ) = 1 1 = 1 1 = r ¢ 1 + r ¢ 1 v2 w2 r(v2 + w2) rv2 + rw2 v2 w2 The fourth µ ¶ µ ¶ µ ¶ µ ¶ v (rs)v r(sv ) v (rs) ¢ 1 = 1 = 1 = r ¢ (s ¢ 1 ) v2 (rs)v2 r(sv2) v2 and fifth conditions are also easy. µ ¶ µ ¶ µ ¶ v 1v v 1 ¢ 1 = 1 = 1 v2 1v2 v2 In a similar way, each Rn is a vector space with the usual operations of vector addition and scalar multiplication. (In R1, we usually do not write the members as column vectors, i.e., we usually do not write ‘(¼)’. Instead we just write ‘¼’.) 1.4 Example This subset of R3 that is a plane through the origin 0 1 x ¯ P = f@yA ¯ x + y + z = 0g z is a vector space if ‘+’ and ‘¢’ are interpreted in this way. 0 1 0 1 0 1 0 1 0 1 x1 x2 x1 + x2 x rx @y1A + @y2A = @y1 + y2 A r ¢ @yA = @ryA z1 z2 z1 + z2 z rz The addition and scalar multiplication operations here are just the ones of R3, reused on its subset P . We say that P inherits these operations from R3. This example of an addition in P 0 1 0 1 0 1 1 ¡1 0 @ 1 A + @ 0 A = @ 1 A ¡2 1 ¡1 illustrates that P is closed under addition. We’ve added two vectors from P — that is, with the property that the sum of their three entries is zero — and the result is a vector also in P . Of course, this example of closure is not a proof of closure. To prove that P is closed under addition, take two elements of P 0 1 0 1 x1 x2 @y1 A @y2 A z1 z2 Edited by Foxit PDF Editor Copyright (c) by Foxit Software Company, 2004 For Evaluation Only. Section I. Definition of Vector Space 83 (membership in P means that x1 + y1 + z1 = 0 and x2 + y2 + z2 = 0), and observe that their sum 0 1 x1 + x2 @y1 + y2 A z1 + z2 is also in P since its entries add (x1 + x2) + (y1 + y2) + (z1 + z2) = (x1 + y1 + z1) + (x2 + y2 + z2) to 0.
Load more

Recommended publications
  • Introduction to Linear Bialgebra
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by University of New Mexico University of New Mexico UNM Digital Repository Mathematics and Statistics Faculty and Staff Publications Academic Department Resources 2005 INTRODUCTION TO LINEAR BIALGEBRA Florentin Smarandache University of New Mexico, [email protected] W.B. Vasantha Kandasamy K. Ilanthenral Follow this and additional works at: https://digitalrepository.unm.edu/math_fsp Part of the Algebra Commons, Analysis Commons, Discrete Mathematics and Combinatorics Commons, and the Other Mathematics Commons Recommended Citation Smarandache, Florentin; W.B. Vasantha Kandasamy; and K. Ilanthenral. "INTRODUCTION TO LINEAR BIALGEBRA." (2005). https://digitalrepository.unm.edu/math_fsp/232 This Book is brought to you for free and open access by the Academic Department Resources at UNM Digital Repository. It has been accepted for inclusion in Mathematics and Statistics Faculty and Staff Publications by an authorized administrator of UNM Digital Repository. For more information, please contact [email protected], [email protected], [email protected]. INTRODUCTION TO LINEAR BIALGEBRA W. B. Vasantha Kandasamy Department of Mathematics Indian Institute of Technology, Madras Chennai – 600036, India e-mail: [email protected] web: http://mat.iitm.ac.in/~wbv Florentin Smarandache Department of Mathematics University of New Mexico Gallup, NM 87301, USA e-mail: [email protected] K. Ilanthenral Editor, Maths Tiger, Quarterly Journal Flat No.11, Mayura Park, 16, Kazhikundram Main Road, Tharamani, Chennai – 600 113, India e-mail: [email protected] HEXIS Phoenix, Arizona 2005 1 This book can be ordered in a paper bound reprint from: Books on Demand ProQuest Information & Learning (University of Microfilm International) 300 N.
    [Show full text]
  • 21. Orthonormal Bases
    21. Orthonormal Bases The canonical/standard basis 011 001 001 B C B C B C B0C B1C B0C e1 = B.C ; e2 = B.C ; : : : ; en = B.C B.C B.C B.C @.A @.A @.A 0 0 1 has many useful properties. • Each of the standard basis vectors has unit length: q p T jjeijj = ei ei = ei ei = 1: • The standard basis vectors are orthogonal (in other words, at right angles or perpendicular). T ei ej = ei ej = 0 when i 6= j This is summarized by ( 1 i = j eT e = δ = ; i j ij 0 i 6= j where δij is the Kronecker delta. Notice that the Kronecker delta gives the entries of the identity matrix. Given column vectors v and w, we have seen that the dot product v w is the same as the matrix multiplication vT w. This is the inner product on n T R . We can also form the outer product vw , which gives a square matrix. 1 The outer product on the standard basis vectors is interesting. Set T Π1 = e1e1 011 B C B0C = B.C 1 0 ::: 0 B.C @.A 0 01 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 0 . T Πn = enen 001 B C B0C = B.C 0 0 ::: 1 B.C @.A 1 00 0 ::: 01 B C B0 0 ::: 0C = B. .C B. .C @. .A 0 0 ::: 1 In short, Πi is the diagonal square matrix with a 1 in the ith diagonal position and zeros everywhere else.
    [Show full text]
  • Arxiv:0704.2561V2 [Math.QA] 27 Apr 2007 Nttto O Xeln Okn Odtos H Eoda Second the Conditions
    DUAL FEYNMAN TRANSFORM FOR MODULAR OPERADS J. CHUANG AND A. LAZAREV Abstract. We introduce and study the notion of a dual Feynman transform of a modular operad. This generalizes and gives a conceptual explanation of Kontsevich’s dual construction producing graph cohomology classes from a contractible differential graded Frobenius alge- bra. The dual Feynman transform of a modular operad is indeed linear dual to the Feynman transform introduced by Getzler and Kapranov when evaluated on vacuum graphs. In marked contrast to the Feynman transform, the dual notion admits an extremely simple presentation via generators and relations; this leads to an explicit and easy description of its algebras. We discuss a further generalization of the dual Feynman transform whose algebras are not neces- sarily contractible. This naturally gives rise to a two-colored graph complex analogous to the Boardman-Vogt topological tree complex. Contents Introduction 1 Notation and conventions 2 1. Main construction 4 2. Twisted modular operads and their algebras 8 3. Algebras over the dual Feynman transform 12 4. Stable graph complexes 13 4.1. Commutative case 14 4.2. Associative case 15 5. Examples 17 6. Moduli spaces of metric graphs 19 6.1. Commutative case 19 6.2. Associative case 21 7. BV-resolution of a modular operad 22 7.1. Basic construction and description of algebras 22 7.2. Stable BV-graph complexes 23 References 26 Introduction arXiv:0704.2561v2 [math.QA] 27 Apr 2007 The relationship between operadic algebras and various moduli spaces goes back to Kontse- vich’s seminal papers [19] and [20] where graph homology was also introduced.
    [Show full text]
  • Determinant Notes
    68 UNIT FIVE DETERMINANTS 5.1 INTRODUCTION In unit one the determinant of a 2× 2 matrix was introduced and used in the evaluation of a cross product. In this chapter we extend the definition of a determinant to any size square matrix. The determinant has a variety of applications. The value of the determinant of a square matrix A can be used to determine whether A is invertible or noninvertible. An explicit formula for A–1 exists that involves the determinant of A. Some systems of linear equations have solutions that can be expressed in terms of determinants. 5.2 DEFINITION OF THE DETERMINANT a11 a12 Recall that in chapter one the determinant of the 2× 2 matrix A = was a21 a22 defined to be the number a11a22 − a12 a21 and that the notation det (A) or A was used to represent the determinant of A. For any given n × n matrix A = a , the notation A [ ij ]n×n ij will be used to denote the (n −1)× (n −1) submatrix obtained from A by deleting the ith row and the jth column of A. The determinant of any size square matrix A = a is [ ij ]n×n defined recursively as follows. Definition of the Determinant Let A = a be an n × n matrix. [ ij ]n×n (1) If n = 1, that is A = [a11], then we define det (A) = a11 . n 1k+ (2) If na>=1, we define det(A) ∑(-1)11kk det(A ) k=1 Example If A = []5 , then by part (1) of the definition of the determinant, det (A) = 5.
    [Show full text]
  • Linear Algebra for Dummies
    Linear Algebra for Dummies Jorge A. Menendez October 6, 2017 Contents 1 Matrices and Vectors1 2 Matrix Multiplication2 3 Matrix Inverse, Pseudo-inverse4 4 Outer products 5 5 Inner Products 5 6 Example: Linear Regression7 7 Eigenstuff 8 8 Example: Covariance Matrices 11 9 Example: PCA 12 10 Useful resources 12 1 Matrices and Vectors An m × n matrix is simply an array of numbers: 2 3 a11 a12 : : : a1n 6 a21 a22 : : : a2n 7 A = 6 7 6 . 7 4 . 5 am1 am2 : : : amn where we define the indexing Aij = aij to designate the component in the ith row and jth column of A. The transpose of a matrix is obtained by flipping the rows with the columns: 2 3 a11 a21 : : : an1 6 a12 a22 : : : an2 7 AT = 6 7 6 . 7 4 . 5 a1m a2m : : : anm T which evidently is now an n × m matrix, with components Aij = Aji = aji. In other words, the transpose is obtained by simply flipping the row and column indeces. One particularly important matrix is called the identity matrix, which is composed of 1’s on the diagonal and 0’s everywhere else: 21 0 ::: 03 60 1 ::: 07 6 7 6. .. .7 4. .5 0 0 ::: 1 1 It is called the identity matrix because the product of any matrix with the identity matrix is identical to itself: AI = A In other words, I is the equivalent of the number 1 for matrices. For our purposes, a vector can simply be thought of as a matrix with one column1: 2 3 a1 6a2 7 a = 6 7 6 .
    [Show full text]
  • Eigenvalues and Eigenvectors
    Jim Lambers MAT 605 Fall Semester 2015-16 Lecture 14 and 15 Notes These notes correspond to Sections 4.4 and 4.5 in the text. Eigenvalues and Eigenvectors In order to compute the matrix exponential eAt for a given matrix A, it is helpful to know the eigenvalues and eigenvectors of A. Definitions and Properties Let A be an n × n matrix. A nonzero vector x is called an eigenvector of A if there exists a scalar λ such that Ax = λx: The scalar λ is called an eigenvalue of A, and we say that x is an eigenvector of A corresponding to λ. We see that an eigenvector of A is a vector for which matrix-vector multiplication with A is equivalent to scalar multiplication by λ. Because x is nonzero, it follows that if x is an eigenvector of A, then the matrix A − λI is singular, where λ is the corresponding eigenvalue. Therefore, λ satisfies the equation det(A − λI) = 0: The expression det(A−λI) is a polynomial of degree n in λ, and therefore is called the characteristic polynomial of A (eigenvalues are sometimes called characteristic values). It follows from the fact that the eigenvalues of A are the roots of the characteristic polynomial that A has n eigenvalues, which can repeat, and can also be complex, even if A is real. However, if A is real, any complex eigenvalues must occur in complex-conjugate pairs. The set of eigenvalues of A is called the spectrum of A, and denoted by λ(A). This terminology explains why the magnitude of the largest eigenvalues is called the spectral radius of A.
    [Show full text]
  • Algebra of Linear Transformations and Matrices Math 130 Linear Algebra
    Then the two compositions are 0 −1 1 0 0 1 BA = = 1 0 0 −1 1 0 Algebra of linear transformations and 1 0 0 −1 0 −1 AB = = matrices 0 −1 1 0 −1 0 Math 130 Linear Algebra D Joyce, Fall 2013 The products aren't the same. You can perform these on physical objects. Take We've looked at the operations of addition and a book. First rotate it 90◦ then flip it over. Start scalar multiplication on linear transformations and again but flip first then rotate 90◦. The book ends used them to define addition and scalar multipli- up in different orientations. cation on matrices. For a given basis β on V and another basis γ on W , we have an isomorphism Matrix multiplication is associative. Al- γ ' φβ : Hom(V; W ) ! Mm×n of vector spaces which though it's not commutative, it is associative. assigns to a linear transformation T : V ! W its That's because it corresponds to composition of γ standard matrix [T ]β. functions, and that's associative. Given any three We also have matrix multiplication which corre- functions f, g, and h, we'll show (f ◦ g) ◦ h = sponds to composition of linear transformations. If f ◦ (g ◦ h) by showing the two sides have the same A is the standard matrix for a transformation S, values for all x. and B is the standard matrix for a transformation T , then we defined multiplication of matrices so ((f ◦ g) ◦ h)(x) = (f ◦ g)(h(x)) = f(g(h(x))) that the product AB is be the standard matrix for S ◦ T .
    [Show full text]
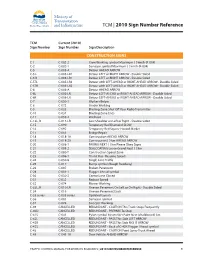
  • 2010 Sign Number Reference for Traffic Control Manual
    TCM | 2010 Sign Number Reference TCM Current (2010) Sign Number Sign Number Sign Description CONSTRUCTION SIGNS C-1 C-002-2 Crew Working symbol Maximum ( ) km/h (R-004) C-2 C-002-1 Surveyor symbol Maximum ( ) km/h (R-004) C-5 C-005-A Detour AHEAD ARROW C-5 L C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5 R C-005-LR1 Detour LEFT or RIGHT ARROW - Double Sided C-5TL C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-5TR C-005-LR2 Detour with LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6 C-006-A Detour AHEAD ARROW C-6L C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-6R C-006-LR Detour LEFT-AHEAD or RIGHT-AHEAD ARROW - Double Sided C-7 C-050-1 Workers Below C-8 C-072 Grader Working C-9 C-033 Blasting Zone Shut Off Your Radio Transmitter C-10 C-034 Blasting Zone Ends C-11 C-059-2 Washout C-13L, R C-013-LR Low Shoulder on Left or Right - Double Sided C-15 C-090 Temporary Red Diamond SLOW C-16 C-092 Temporary Red Square Hazard Marker C-17 C-051 Bridge Repair C-18 C-018-1A Construction AHEAD ARROW C-19 C-018-2A Construction ( ) km AHEAD ARROW C-20 C-008-1 PAVING NEXT ( ) km Please Obey Signs C-21 C-008-2 SEALCOATING Loose Gravel Next ( ) km C-22 C-080-T Construction Speed Zone C-23 C-086-1 Thank You - Resume Speed C-24 C-030-8 Single Lane Traffic C-25 C-017 Bump symbol (Rough Roadway) C-26 C-007 Broken Pavement C-28 C-001-1 Flagger Ahead symbol C-30 C-030-2 Centre Lane Closed C-31 C-032 Reduce Speed C-32 C-074 Mower Working C-33L, R C-010-LR Uneven Pavement On Left or On Right - Double Sided C-34
    [Show full text]
  • Math 217: Multilinearity of Determinants Professor Karen Smith (C)2015 UM Math Dept Licensed Under a Creative Commons By-NC-SA 4.0 International License
    Math 217: Multilinearity of Determinants Professor Karen Smith (c)2015 UM Math Dept licensed under a Creative Commons By-NC-SA 4.0 International License. A. Let V −!T V be a linear transformation where V has dimension n. 1. What is meant by the determinant of T ? Why is this well-defined? Solution note: The determinant of T is the determinant of the B-matrix of T , for any basis B of V . Since all B-matrices of T are similar, and similar matrices have the same determinant, this is well-defined—it doesn't depend on which basis we pick. 2. Define the rank of T . Solution note: The rank of T is the dimension of the image. 3. Explain why T is an isomorphism if and only if det T is not zero. Solution note: T is an isomorphism if and only if [T ]B is invertible (for any choice of basis B), which happens if and only if det T 6= 0. 3 4. Now let V = R and let T be rotation around the axis L (a line through the origin) by an 21 0 0 3 3 angle θ. Find a basis for R in which the matrix of ρ is 40 cosθ −sinθ5 : Use this to 0 sinθ cosθ compute the determinant of T . Is T othogonal? Solution note: Let v be any vector spanning L and let u1; u2 be an orthonormal basis ? for V = L . Rotation fixes ~v, which means the B-matrix in the basis (v; u1; u2) has 213 first column 405.
    [Show full text]
  • Determinants Math 122 Calculus III D Joyce, Fall 2012
    Determinants Math 122 Calculus III D Joyce, Fall 2012 What they are. A determinant is a value associated to a square array of numbers, that square array being called a square matrix. For example, here are determinants of a general 2 × 2 matrix and a general 3 × 3 matrix. a b = ad − bc: c d a b c d e f = aei + bfg + cdh − ceg − afh − bdi: g h i The determinant of a matrix A is usually denoted jAj or det (A). You can think of the rows of the determinant as being vectors. For the 3×3 matrix above, the vectors are u = (a; b; c), v = (d; e; f), and w = (g; h; i). Then the determinant is a value associated to n vectors in Rn. There's a general definition for n×n determinants. It's a particular signed sum of products of n entries in the matrix where each product is of one entry in each row and column. The two ways you can choose one entry in each row and column of the 2 × 2 matrix give you the two products ad and bc. There are six ways of chosing one entry in each row and column in a 3 × 3 matrix, and generally, there are n! ways in an n × n matrix. Thus, the determinant of a 4 × 4 matrix is the signed sum of 24, which is 4!, terms. In this general definition, half the terms are taken positively and half negatively. In class, we briefly saw how the signs are determined by permutations.
    [Show full text]
  • Glossary of Linear Algebra Terms
    INNER PRODUCT SPACES AND THE GRAM-SCHMIDT PROCESS A. HAVENS 1. The Dot Product and Orthogonality 1.1. Review of the Dot Product. We first recall the notion of the dot product, which gives us a familiar example of an inner product structure on the real vector spaces Rn. This product is connected to the Euclidean geometry of Rn, via lengths and angles measured in Rn. Later, we will introduce inner product spaces in general, and use their structure to define general notions of length and angle on other vector spaces. Definition 1.1. The dot product of real n-vectors in the Euclidean vector space Rn is the scalar product · : Rn × Rn ! R given by the rule n n ! n X X X (u; v) = uiei; viei 7! uivi : i=1 i=1 i n Here BS := (e1;:::; en) is the standard basis of R . With respect to our conventions on basis and matrix multiplication, we may also express the dot product as the matrix-vector product 2 3 v1 6 7 t î ó 6 . 7 u v = u1 : : : un 6 . 7 : 4 5 vn It is a good exercise to verify the following proposition. Proposition 1.1. Let u; v; w 2 Rn be any real n-vectors, and s; t 2 R be any scalars. The Euclidean dot product (u; v) 7! u · v satisfies the following properties. (i:) The dot product is symmetric: u · v = v · u. (ii:) The dot product is bilinear: • (su) · v = s(u · v) = u · (sv), • (u + v) · w = u · w + v · w.
    [Show full text]
  • Math 2331 – Linear Algebra 6.2 Orthogonal Sets
    6.2 Orthogonal Sets Math 2331 { Linear Algebra 6.2 Orthogonal Sets Jiwen He Department of Mathematics, University of Houston [email protected] math.uh.edu/∼jiwenhe/math2331 Jiwen He, University of Houston Math 2331, Linear Algebra 1 / 12 6.2 Orthogonal Sets Orthogonal Sets Basis Projection Orthonormal Matrix 6.2 Orthogonal Sets Orthogonal Sets: Examples Orthogonal Sets: Theorem Orthogonal Basis: Examples Orthogonal Basis: Theorem Orthogonal Projections Orthonormal Sets Orthonormal Matrix: Examples Orthonormal Matrix: Theorems Jiwen He, University of Houston Math 2331, Linear Algebra 2 / 12 6.2 Orthogonal Sets Orthogonal Sets Basis Projection Orthonormal Matrix Orthogonal Sets Orthogonal Sets n A set of vectors fu1; u2;:::; upg in R is called an orthogonal set if ui · uj = 0 whenever i 6= j. Example 82 3 2 3 2 39 < 1 1 0 = Is 4 −1 5 ; 4 1 5 ; 4 0 5 an orthogonal set? : 0 0 1 ; Solution: Label the vectors u1; u2; and u3 respectively. Then u1 · u2 = u1 · u3 = u2 · u3 = Therefore, fu1; u2; u3g is an orthogonal set. Jiwen He, University of Houston Math 2331, Linear Algebra 3 / 12 6.2 Orthogonal Sets Orthogonal Sets Basis Projection Orthonormal Matrix Orthogonal Sets: Theorem Theorem (4) Suppose S = fu1; u2;:::; upg is an orthogonal set of nonzero n vectors in R and W =spanfu1; u2;:::; upg. Then S is a linearly independent set and is therefore a basis for W . Partial Proof: Suppose c1u1 + c2u2 + ··· + cpup = 0 (c1u1 + c2u2 + ··· + cpup) · = 0· (c1u1) · u1 + (c2u2) · u1 + ··· + (cpup) · u1 = 0 c1 (u1 · u1) + c2 (u2 · u1) + ··· + cp (up · u1) = 0 c1 (u1 · u1) = 0 Since u1 6= 0, u1 · u1 > 0 which means c1 = : In a similar manner, c2,:::,cp can be shown to by all 0.
    [Show full text]