DOCSLIB.ORG

Principles of Astronomy: Possible Topics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Principles of Astronomy: Possible Topics Principles of Astronomy: Possible Topics J. M. Veal, Ph. D. version 20.03.03 Contents 5 Solar System 19 5.1 Overview of Solar System Objects . 19 1 Introduction 2 5.2 Space Exploraton: Past & Present . 19 1.1 Cosmic Perspective . .2 5.3 Aurora Borealis . 21 1.2 Nature of Science . .3 5.4 Introduction to Terrestrial Planets & K ...... 21 5.5 Interiors of Terrestrial Planets & K ......... 21 2 Basics 4 5.6 Surfaces of Terrestrial Planets & K ......... 22 2.1 Sky Coordinates . .4 5.7 Atmospheres of Terrestrial Planets . 22 2.2 Earth's Rotation . .4 5.8 Mythology of Terrestrial Planets in Brief . 23 2.3 Precession . .4 5.9 Introduction to Jovian Planets . 23 2.4 Appearance of Stars . .4 5.10 Atmospheres of Jovian Planets . 23 2.5 Seasons . .4 5.11 Interiors & Magnetic Fields of Jovian Planets . 23 2.6 Lunar Phases . .5 5.12 Mythology of Jovian Planets in Brief . 24 2.7 Days & Months . .5 5.13 Moons . 24 2.8 Eclipses . .5 5.14 Rings . 24 2.9 Retrograde Motion . .5 5.15 Dwarf Planets . 24 2.10 Kepler's Laws of Planetary Motion . .6 5.16 Asteroids & Comets . 25 2.11 Newton's Laws of Motion . .6 5.17 TNO's . 26 2.12 Newton's Universal Law of Gravitation . .6 5.18 Meteors . 26 2.13 Tides . .6 6 Stars 26 3 Fundamental Concepts 7 6.1 Star Formation in Brief . 26 3.1 Electromagnetic Radiation in Brief . .7 6.2 Star Formation . 26 3.2 Electromagnetic Radiation . .7 6.3 Nuclear Fusion . 27 3.3 Observing Instruments & Techniques . .7 6.4 Limb Darkening . 28 3.4 Temperature . .8 6.5 Sunspots in Brief . 28 3.5 Thermal Radiation . .8 6.6 Sunspots . 29 3.6 Scattering . .8 6.7 Stellar Evolution & the H-R Diagram . 29 3.7 The Classical Atom . .8 6.8 Life of Our Sun . 30 3.8 Quanta, Absorption, & Emission . .9 6.9 Supergiants & Supernovae . 31 3.9 Spectral Lines . .9 6.10 Neutron Stars & Pulsars . 32 3.10 Ionization, Recombination, & Cascade . 10 6.11 Binary Stars . 32 3.11 Collisional vs. Radiative Processes . 10 6.12 Novae . 33 3.12 Magnetic Fields . 10 6.13 Cosmic Recycling . 33 3.13 Doppler Shift . 10 3.14 Parallax . 11 7 Galaxies 33 3.15 Proper Motion & Radial Velocity . 11 7.1 Overview of Galaxies . 33 7.2 AGN . 33 4 Physical Principles 12 7.3 Dark Matter . 34 4.1 Special Relativity . 12 4.2 Duality Of Light . 13 4.3 Uncertainty Principle . 14 4.4 Quantum States . 16 4.5 Exclusion Principle . 17 4.6 Matter & Antimatter . 17 4.7 Arrow of Time . 18 1 J. M. Veal, Principles of Astronomy 2 8 Black Holes & Cosmology 34 1 Introduction 8.1 Early Universe . 34 8.2 Curved Spacetime . 35 1.1 Cosmic Perspective 8.3 General Relativity . 36 What is large? What is small? Consider walking from San 8.4 Black Holes in Brief . 36 • Diego to Los Angeles. An example of a scale model is a 8.5 Black Holes . 37 globe. Perhaps the scale is 1 inch = 1000 miles. 8.6 Gravitational Redshift . 39 8.7 Hubble's Law & Hubble Distance . 39 Solar System. 8.8 Cosmological Redshift . 39 • What is the solar system? For now, let's say Sun, planets, 8.9 Big Bang . 40 moons, asteroids, & comets (no other stars!). (\My Very 8.10 Cosmic Microwave Background . 40 Excellent Mother Just Served Us Noodles.") 8.11 Hubble Parameter & Observable Edge . 40 8.12 Cosmic Horizon & Dark Energy . 41 The scale is 1:1010. (In astronomy we use scientific notation 8.13 Fate of the Universe . 42 for large numbers.) No units are needed because they're the same on both sides. (A person would be 107 miles tall in 9 Life in the Universe 42 this model.1) 9.1 Interstellar Chemistry . 42 The relative sizes are easy to show in a book or on a screen, 9.2 Comets . 43 as are the relative distances. [sketches 1 & 2] But showing 9.3 Search for Extrasolar Planets . 44 both the relative sizes and distances in the a single scale 9.4 Origin of Life . 44 model can't be done in a book or on a screen. Could we 9.5 Nature of Life . 45 walk to α Centauri, 4.4 light years away? 9.6 Definitions . 45 9.7 Possible Existence of Extrasolar Intelligence . 46 Milky Way. 9.8 Search for Extraterrestrial Intelligence . 46 • What is the Milky Way? It's our galaxy, full of stars, dust, 11 10 Miscellaneous 47 & gas. There are more than 10 stars in our galaxy. How 10.1 Pseudoscience . 47 much is a hundred billion? (Consider salt in Qualcomm...) 10.2 Exam Instructions & Answer Sheet . 48 The scale is 1:1019. Or, 1 mm = 1 light year. (A light year is the distance light travels in one year, roughly equal to 1013 km.) Or, atom-size = star-size. In this model, our Milky Way would be the size of a football field { with the Sun at about the 20 yd. line. Alternate Milky Way model. • If the d is a grain of NaCl, the next grain is 7 miles away. This model is useful when visualizing galaxy collisions. Universe. • The universe is everything that exists. There are more than 1011 galaxies in the universe. Ñ 1022 stars. How much is 1022? (Consider grains of sand... ) In astronomy, it's not acceptable to confuse the solar system, • the galaxy, and the universe.2 Time. • Now the scale model is 1 year = age of universe. (The age of the universe is about 13.8 billion years.) January 1: big bang (the beginning of space, time, matter, energy, force, ...) February: Milky Way forms September 3: Earth forms September 22: earliest life on Earth December 26: rise of dinosaurs December 30: extinction of dinosaurs Dec. 31, 9 p.m.: earliest human ancestors 1Model sizes in mm for the Sun and 8 planets are as follows: 139, .5, 1.2, 1.3, .7 14.3, 12.0, 5.2, and 4.8. Model distances in m from the Sun to the 8 planets are as follows: 6, 11, 15, 23, 78, 143, 287, and 450. 2htwins.net; The Known Universe by AMNH; cosmic eye; atlasoftheuni- verse.com; Cosmic Voyage. J. M. Veal, Principles of Astronomy 3 Dec. 31, 11:58 p.m.: first modern humans { R. Descartes? What can we be absolutely sure of? Dec. 31, 11:59:25 p.m.: rise of agriculture Might we be dreaming? He says cogito ergo sum, and that we can be sure of it. His argument appeals to our Dec. 31, 11:59:49 p.m.: pyramids at Giza intuition and common sense, but these cannot be relied Dec. 31, 11:59:59 p.m.: Kepler, Galileo upon in these matters. (Consider \eivocae"...) Motions. • Science seeks to describe what we observe, to find patterns, How does Earth move? Like a top on a record player on a • and to make subsequent predictions. (Consider learing grav- merry-go-round. ity...) motion speed period rotation 600 mph 1 day When evidence contradicts a theory, the theory must be precession 26,000 yrs • changed or dismissed in favor of a new theory. (Consider revolution 60,000 mph 1 year a helium balloon...) galactic orbit w/ \bounce" 600,000 mph 230 ¢ 106 yrs Milky Way toward Andromeda 180,000 mph Science seeks to explain these patterns with the simplest • expansion of universe v H0r answer (like Ockham's Razor). Reading. What does simple mean3 and what is a simple theory? To • answer this, we must consider the number of initial condi- { TCPF2: Chapter 1, Sections 1 - 2. tions needed for the theory to happen (like the ingredients in a recipe) and the number of characteristics or parts of the Homework. • theory (like the steps in a recipe). 1. (3 points) List the eight planets in order of increasing distance from the Sun. { Consider a statement that describes a wrinkled piece of 2. (5 points) Planet A is roughly how many times further paper. How many statements are necessary to describe from the Sun than the Earth is? (Planet A can be any the chalk completely and exactly? One for the velocity of the seven other planets.) and position of every electron, proton, neutron, etc. We see that even a piece of chalk is far from simple. 3. (8 points) Consider our scale model of the solar system. (Simple: photon(1), black hole(3).) How far would we have to walk to reach the d's near- est neighbor, α Centauri? (To answer this question, { Consider an example in which science must choose, you must set up the appropriate ratio and solve for the based on simplicity, between two theories. (Neither can correct quantity.) be proven; neither can be disproven.) A) The universe was created 5 minutes ago with all of our memories in 4. (8 points) Consider our two visualized models of our tact { far from simple. B) The big bang theory { simple galaxy, the Milky Way. In the first, stars were the size compared to A. of an atom, α Centauri was 4.4 millimeters from the d, and the galaxy was 100 yards across. In the second, Further lines of thought include the following. stars were the size of a grain of salt, α Centauri was • 7 miles from the d, and our galaxy would be how far \Absence of evidence isn't evidence of absence." across? (To answer this question, you must set up the \What cannot be settled by experiment is not worth debat- appropriate ratio and solve for the correct quantity.) ing."4 5.
Load more

Recommended publications
  • Using Concrete Scales: a Practical Framework for Effective Visual Depiction of Complex Measures Fanny Chevalier, Romain Vuillemot, Guia Gali
    Using Concrete Scales: A Practical Framework for Effective Visual Depiction of Complex Measures Fanny Chevalier, Romain Vuillemot, Guia Gali To cite this version: Fanny Chevalier, Romain Vuillemot, Guia Gali. Using Concrete Scales: A Practical Framework for Effective Visual Depiction of Complex Measures. IEEE Transactions on Visualization and Computer Graphics, Institute of Electrical and Electronics Engineers, 2013, 19 (12), pp.2426-2435. 10.1109/TVCG.2013.210. hal-00851733v1 HAL Id: hal-00851733 https://hal.inria.fr/hal-00851733v1 Submitted on 8 Jan 2014 (v1), last revised 8 Jan 2014 (v2) HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. Using Concrete Scales: A Practical Framework for Effective Visual Depiction of Complex Measures Fanny Chevalier, Romain Vuillemot, and Guia Gali a b c Fig. 1. Illustrates popular representations of complex measures: (a) US Debt (Oto Godfrey, Demonocracy.info, 2011) explains the gravity of a 115 trillion dollar debt by progressively stacking 100 dollar bills next to familiar objects like an average-sized human, sports fields, or iconic New York city buildings [15] (b) Sugar stacks (adapted from SugarStacks.com) compares caloric counts contained in various foods and drinks using sugar cubes [32] and (c) How much water is on Earth? (Jack Cook, Woods Hole Oceanographic Institution and Howard Perlman, USGS, 2010) shows the volume of oceans and rivers as spheres whose sizes can be compared to that of Earth [38].
    [Show full text]
  • Biophilia, Gaia, Cosmos, and the Affectively Ecological
    vital reenchantments Before you start to read this book, take this moment to think about making a donation to punctum books, an independent non-profit press, @ https://punctumbooks.com/support/ If you’re reading the e-book, you can click on the image below to go directly to our donations site. Any amount, no matter the size, is appreciated and will help us to keep our ship of fools afloat. Contri- butions from dedicated readers will also help us to keep our commons open and to cultivate new work that can’t find a welcoming port elsewhere. Our ad- venture is not possible without your support. Vive la Open Access. Fig. 1. Hieronymus Bosch, Ship of Fools (1490–1500) vital reenchantments: biophilia, gaia, cosmos, and the affectively ecological. Copyright © 2019 by Lauren Greyson. This work carries a Creative Commons BY-NC-SA 4.0 International license, which means that you are free to copy and redistribute the material in any medium or format, and you may also remix, transform and build upon the material, as long as you clearly attribute the work to the authors (but not in a way that suggests the authors or punctum books endorses you and your work), you do not use this work for commercial gain in any form whatsoever, and that for any remixing and transformation, you distribute your rebuild under the same license. http://creativecommons.org/li- censes/by-nc-sa/4.0/ First published in 2019 by punctum books, Earth, Milky Way. https://punctumbooks.com ISBN-13: 978-1-950192-07-6 (print) ISBN-13: 978-1-950192-08-3 (ePDF) lccn: 2018968577 Library of Congress Cataloging Data is available from the Library of Congress Editorial team: Casey Coffee and Eileen A.
    [Show full text]
  • Detection of PAH and Far-Infrared Emission from the Cosmic Eye
    Accepted for publication in ApJ A Preprint typeset using LTEX style emulateapj v. 08/22/09 DETECTION OF PAH AND FAR-INFRARED EMISSION FROM THE COSMIC EYE: PROBING THE DUST AND STAR FORMATION OF LYMAN BREAK GALAXIES B. Siana1, Ian Smail2, A. M. Swinbank2, J. Richard2, H. I. Teplitz3, K. E. K. Coppin2, R. S. Ellis1, D. P. Stark4, J.-P. Kneib5, A. C. Edge2 Accepted for publication in ApJ ABSTRACT ∗ We report the results of a Spitzer infrared study of the Cosmic Eye, a strongly lensed, LUV Lyman Break Galaxy (LBG) at z =3.074. We obtained Spitzer IRS spectroscopy as well as MIPS 24 and 70 µm photometry. The Eye is detected with high significance at both 24 and 70 µm and, when including +4.7 11 a flux limit at 3.5 mm, we estimate an infrared luminosity of LIR = 8.3−4.4 × 10 L⊙ assuming a magnification of 28±3. This LIR is eight times lower than that predicted from the rest-frame UV properties assuming a Calzetti reddening law. This has also been observed in other young LBGs, and indicates that the dust reddening law may be steeper in these galaxies. The mid-IR spectrum shows strong PAH emission at 6.2 and 7.7 µm, with equivalent widths near the maximum values observed in star-forming galaxies at any redshift. The LP AH -to-LIR ratio lies close to the relation measured in local starbursts. Therefore, LP AH or LMIR may be used to estimate LIR and thus, star formation rate, of LBGs, whose fluxes at longer wavelengths are typically below current confusion limits.
    [Show full text]
  • Close-Up View of a Luminous Star-Forming Galaxy at Z = 2.95 S
    Close-up view of a luminous star-forming galaxy at z = 2.95 S. Berta, A. J. Young, P. Cox, R. Neri, B. M. Jones, A. J. Baker, A. Omont, L. Dunne, A. Carnero Rosell, L. Marchetti, et al. To cite this version: S. Berta, A. J. Young, P. Cox, R. Neri, B. M. Jones, et al.. Close-up view of a luminous star- forming galaxy at z = 2.95. Astronomy and Astrophysics - A&A, EDP Sciences, 2021, 646, pp.A122. 10.1051/0004-6361/202039743. hal-03147428 HAL Id: hal-03147428 https://hal.archives-ouvertes.fr/hal-03147428 Submitted on 19 Feb 2021 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. A&A 646, A122 (2021) Astronomy https://doi.org/10.1051/0004-6361/202039743 & c S. Berta et al. 2021 Astrophysics Close-up view of a luminous star-forming galaxy at z = 2.95? S. Berta1, A. J. Young2, P. Cox3, R. Neri1, B. M. Jones4, A. J. Baker2, A. Omont3, L. Dunne5, A. Carnero Rosell6,7, L. Marchetti8,9,10 , M. Negrello5, C. Yang11, D. A. Riechers12,13, H. Dannerbauer6,7, I.
    [Show full text]
  • NCSA Access Magazine
    CONTACTS NCSA Contacts Directory http://www.ncsa.uiuc.edu/Generai/NCSAContacts.html Allocations Education & Outreach Division Orders for Publications, http://www.ncsa.uiuc.edu/Generai/A IIocations/ApplyTop.html http://www.ncsa.uiuc.edu/edu/EduHome.html NCSA Software, and Multimedia Radha Nandkumar John Ziebarth, Associate Director http://www.ncsa.uiuc.edu/Pubs/ 217-244-0650 217-244-1961 TechResCatalog/TRC.TOC.html [email protected] [email protected] Debbie Shirley [email protected] Applications Division/Faculty Program Education http://www.ncsa.uiuc.ed u/Apps/Apps lntro.html Scott Lathrop Public Information Office Melanie Loots, Associate Director 217-244-1099 http://www.ncsa.uiuc.edu/General/ 217-244-2921 [email protected] PIO/NCSAinfo.html [email protected] i uc.edu John Melchi Outreach 217-244-3049 Al lison Clark (information) Alai na Kanfer 217-244-8195 fax 217-244-0768 217-244-0876 [email protected] [email protected] i uc.edu [email protected] Publications Group Visitors Program Training http://www.ncsa.uiuc.edu/Pubs/ jean Soliday http://www.ncsa.uiuc.edu/General/ Pubslntro.html 217-244-1972 Training/training_homepage.html Melissa Johnson [email protected] u Mary Bea Walker 217-244-0645 217-244-9883 melissaj@ncsa .uiuc.edu Computing & Communications Division mbwalker@ncsa .uiuc.edu http://www.ncsa.uiuc.edu/Generai/CC/CCHome.html Software Development Division Charles Catlett, Associate Director Industrial Program http ://www.ncsa.uiuc.edu/SDG/SDGintro.html 217-333-1163 http://www.ncsa.uiuc.edu/General/lndusProg/ joseph Hardin, Associate Director [email protected] lndProg.html 217-244-7802 John Stevenson, Corporate Officer hardin@ncsa .uiuc.edu Ken Sartain (i nformation) 217-244-0474 217-244-0103 [email protected] jae Allen (information) sartain@ ncsa.u iuc.edu 217-244-3364 Marketing Communications Division [email protected] Consulting Services http://www.ncsa.uiuc.edu/Generai/MarComm/ http://www.ncsa.
    [Show full text]
  • Archons (Commanders) [NOTICE: They Are NOT Anlien Parasites], and Then, in a Mirror Image of the Great Emanations of the Pleroma, Hundreds of Lesser Angels
    A R C H O N S HIDDEN RULERS THROUGH THE AGES A R C H O N S HIDDEN RULERS THROUGH THE AGES WATCH THIS IMPORTANT VIDEO UFOs, Aliens, and the Question of Contact MUST-SEE THE OCCULT REASON FOR PSYCHOPATHY Organic Portals: Aliens and Psychopaths KNOWLEDGE THROUGH GNOSIS Boris Mouravieff - GNOSIS IN THE BEGINNING ...1 The Gnostic core belief was a strong dualism: that the world of matter was deadening and inferior to a remote nonphysical home, to which an interior divine spark in most humans aspired to return after death. This led them to an absorption with the Jewish creation myths in Genesis, which they obsessively reinterpreted to formulate allegorical explanations of how humans ended up trapped in the world of matter. The basic Gnostic story, which varied in details from teacher to teacher, was this: In the beginning there was an unknowable, immaterial, and invisible God, sometimes called the Father of All and sometimes by other names. “He” was neither male nor female, and was composed of an implicitly finite amount of a living nonphysical substance. Surrounding this God was a great empty region called the Pleroma (the fullness). Beyond the Pleroma lay empty space. The God acted to fill the Pleroma through a series of emanations, a squeezing off of small portions of his/its nonphysical energetic divine material. In most accounts there are thirty emanations in fifteen complementary pairs, each getting slightly less of the divine material and therefore being slightly weaker. The emanations are called Aeons (eternities) and are mostly named personifications in Greek of abstract ideas.
    [Show full text]
  • Ast110fall2015-Labmanual.Pdf
    2015/2016 (http://astronomy.nmsu.edu/astro/Ast110Fall2015.pdf) 1 2 Contents 1IntroductiontotheAstronomy110Labs 5 2TheOriginoftheSeasons 21 3TheSurfaceoftheMoon 41 4ShapingSurfacesintheSolarSystem:TheImpactsofCometsand Asteroids 55 5IntroductiontotheGeologyoftheTerrestrialPlanets 69 6Kepler’sLawsandGravitation 87 7TheOrbitofMercury 107 8MeasuringDistancesUsingParallax 121 9Optics 135 10 The Power of Light: Understanding Spectroscopy 151 11 Our Sun 169 12 The Hertzsprung-Russell Diagram 187 3 13 Mapping the Galaxy 203 14 Galaxy Morphology 219 15 How Many Galaxies Are There in the Universe? 241 16 Hubble’s Law: Finding the Age of the Universe 255 17 World-Wide Web (Extra-credit/Make-up) Exercise 269 AFundamentalQuantities 271 BAccuracyandSignificantDigits 273 CUnitConversions 274 DUncertaintiesandErrors 276 4 Name: Lab 1 Introduction to the Astronomy 110 Labs 1.1 Introduction Astronomy is a physical science. Just like biology, chemistry, geology, and physics, as- tronomers collect data, analyze that data, attempt to understand the object/subject they are looking at, and submit their results for publication. Along thewayas- tronomers use all of the mathematical techniques and physics necessary to understand the objects they examine. Thus, just like any other science, a largenumberofmath- ematical tools and concepts are needed to perform astronomical research. In today’s introductory lab, you will review and learn some of the most basic concepts neces- sary to enable you to successfully complete the various laboratory exercises you will encounter later this semester. When needed, the weekly laboratory exercise you are performing will refer back to the examples in this introduction—so keep the worked examples you will do today with you at all times during the semester to use as a refer- ence when you run into these exercises later this semester (in fact, on some occasions your TA might have you redo one of the sections of this lab for review purposes).
    [Show full text]
  • UC San Diego UC San Diego Electronic Theses and Dissertations
    UC San Diego UC San Diego Electronic Theses and Dissertations Title The science of the stars in Danzig from Rheticus to Hevelius / Permalink https://escholarship.org/uc/item/7n41x7fd Author Jensen, Derek Publication Date 2006 Peer reviewed|Thesis/dissertation eScholarship.org Powered by the California Digital Library University of California UNIVERSITY OF CALIFORNIA, SAN DIEGO THE SCIENCE OF THE STARS IN DANZIG FROM RHETICUS TO HEVELIUS A dissertation submitted in partial satisfaction of the requirements for the degree Doctor of Philosophy in History (Science Studies) by Derek Jensen Committee in charge: Professor Robert S. Westman, Chair Professor Luce Giard Professor John Marino Professor Naomi Oreskes Professor Donald Rutherford 2006 The dissertation of Derek Jensen is approved, and it is acceptable in quality and form for publication on microfilm: _________________________________________ _________________________________________ _________________________________________ _________________________________________ _________________________________________ Chair University of California, San Diego 2006 iii FOR SARA iv TABLE OF CONTENTS Signature Page........................................................................................................... iii Dedication ................................................................................................................. iv Table of Contents ...................................................................................................... v List of Figures ..........................................................................................................
    [Show full text]
  • 12 Strong Gravitational Lenses
    12 Strong Gravitational Lenses Phil Marshall, MaruˇsaBradaˇc,George Chartas, Gregory Dobler, Ard´ısEl´ıasd´ottir,´ Emilio Falco, Chris Fassnacht, James Jee, Charles Keeton, Masamune Oguri, Anthony Tyson LSST will contain more strong gravitational lensing events than any other survey preceding it, and will monitor them all at a cadence of a few days to a few weeks. Concurrent space-based optical or perhaps ground-based surveys may provide higher resolution imaging: the biggest advances in strong lensing science made with LSST will be in those areas that benefit most from the large volume and the high accuracy, multi-filter time series. In this chapter we propose an array of science projects that fit this bill. We first provide a brief introduction to the basic physics of gravitational lensing, focusing on the formation of multiple images: the strong lensing regime. Further description of lensing phenomena will be provided as they arise throughout the chapter. We then make some predictions for the properties of samples of lenses of various kinds we can expect to discover with LSST: their numbers and distributions in redshift, image separation, and so on. This is important, since the principal step forward provided by LSST will be one of lens sample size, and the extent to which new lensing science projects will be enabled depends very much on the samples generated. From § 12.3 onwards we introduce the proposed LSST science projects. This is by no means an exhaustive list, but should serve as a good starting point for investigators looking to exploit the strong lensing phenomenon with LSST.
    [Show full text]
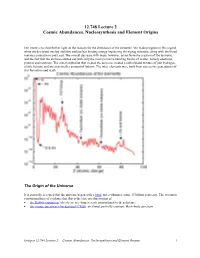
  • 12.748 Lecture 2 Cosmic Abundances, Nucleosynthesis and Element Origins
    12.748 Lecture 2 Cosmic Abundances, Nucleosynthesis and Element Origins Our intent is to shed further light on the reasons for the abundance of the elements. We made progress in this regard when we discussed nuclear stability and nuclear binding energy explaining the zigzag structure, along with the broad maxima around Iron and Lead. The overall decrease with mass, however, arises from the creation of the universe, and the fact that the universe started out with only the most primitive building blocks of matter, namely electrons, protons and neutrons. The initial explosion that created the universe created a rather bland mixture of just hydrogen, a little helium, and an even smaller amount of lithium. The other elements were built from successive generations of star formation and death. The Origin of the Universe It is generally accepted that the universe began with a bang, not a whimper, some 15 billion years ago. The two most convincing lines of evidence that this is the case are observation of • the Hubble expansion: objects are receding at a rate proportional to their distance • the cosmic microwave background (CMB): an almost perfectly isotropic black-body spectrum Isotopes 12.748 Lecture 2: Cosmic Abundances, Nucleosynthesis and Element Origins 1 In the initial fraction of a second, the temperature is so hot that even subatomic particles like neutrons, electrons and protons fall apart into their constituent pieces (quarks and gluons). These temperatures are well beyond anything achievable in the universe since. As the fireball expands, the temperature drops, and progressively higher-level particles are manufactured. By the end of the first second, the temperature has dropped to a mere billion degrees or so, and things are starting to get a little more normal: electrons, neutrons and protons can now exist.
    [Show full text]
  • ASTR/GEOL 3300: ET Life • Logistics: – Your First Day? Pick up a Syllabus, Overview, Etc
    ASTR/GEOL 3300: ET Life • Logistics: – Your first day? Pick up a syllabus, overview, etc. – www.boulder.swri.edu/~kwalsh/ASTR3300 • News: – Homework #1 next week • Plan for Today: – Scale of the Universe – Our place • Next time: Forming Stars and Planets Rebecca’s Office Hours • Office: E122 2:00-4:00 Monday and Wednesday Preliminary HW1 results Question Yes No Mars 22 33 Solar System 35 20 Galaxy 46 9 Universe 48 7 The Greeks Thales – First Greek Astronomer • ~600 BC • Actually asked questions: “What is the Universe made of” • Predicted an eclipse • Also.. Anaximander Pythagoras and Erastothenes Retrograde motion • http://mars.jpl.nasa.gov/allaboutmars/ nightsky/nightsky04/ Ptolemy What did the Greeks know • The planets, Sun and Moon move across the sky, – The Sun moves at a very regular rate, but the line it follows varies with season – The Moon moves at regular rate, and the line it follows is much more regular – Some planets always move the same direction (W-E), – Though others sometimes backtrack-retrograde motion • There were no tools capable of measure absolute sizes, or precise positions Copernicus • FINALLY…. Tycho SN 1572 Kepler Kepler’s 2nd Law Galileo Newton’s Principia • Explained general laws of motion – from which Keplers laws of planetary motion are natural consequences Scale of the Universe: Powers of 10 Scientific notation: • 101 = 10 • 102 = 100 • 103 = 1000 • 106 = 1,000,000 • 109 = 1,000,000,000 • 1011 = 100,000,000,000 • 100 = 1 • 10-1 = 0.1 • 10-2 = 0.01 • Also, common notation: • 1e9 = 109 Eames chair Powers of
    [Show full text]
  • ASTR110G Astronomy Laboratory Exercises C the GEAS Project 2020
    ASTR110G Astronomy Laboratory Exercises c The GEAS Project 2020 ASTR110G Laboratory Exercises Lab 1: Fundamentals of Measurement and Error Analysis ...... ....................... 1 Lab 2: Observing the Sky ............................... ............................. 35 Lab 3: Cratering and the Lunar Surface ................... ........................... 73 Lab 4: Cratering and the Martian Surface ................. ........................... 97 Lab 5: Parallax Measurements and Determining Distances ... ....................... 129 Lab 6: The Hertzsprung-Russell Diagram and Stellar Evolution ..................... 157 Lab 7: Hubble’s Law and the Cosmic Distance Scale ........... ..................... 185 Lab 8: Properties of Galaxies .......................... ............................. 213 Appendix I: Definitions for Keywords ..................... .......................... 249 Appendix II: Supplies ................................. .............................. 263 Lab 1 Fundamentals of Measurement and Error Analysis 1.1 Introduction This laboratory exercise will serve as an introduction to all of the laboratory exercises for this course. We will explore proper techniques for obtaining and analyzing data, and practice plotting and analyzing data. We will discuss a scientific methodology for conducting exper- iments in which we formulate a question, predict the behavior of the system based on likely solutions, acquire relevant data, and then compare our predictions with the observations. You will have a chance to plan a short experiment,
    [Show full text]