DOCSLIB.ORG

Though the Ocean Is Heavily Damped System for the Long-Period Tides, Non-Equilibrium Features Can Be Found. Short Rossby Wave

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Though the Ocean Is Heavily Damped System for the Long-Period Tides, Non-Equilibrium Features Can Be Found. Short Rossby Wave 測 地 学 会 誌,第47巻,第1号 Journal of the Geodetic Society of Japan (2001),551-557頁 Vol.47, No.1, (2001), pp.551-557 Non-equilibrium Characteristics of the Long-Period Ocean Tides from Dynamics and Energetics Takashi Takanezawa*, Koji Matsumoto, Masatsugu Ooe and Isao Naito National Astronomical Observatory, 2-12 Hoshigaoka-cho, Mizusawa-shi, Iwate-ken 023-0861, Japan (Received October 3, 2000; Revised February 7, 2001; Accepted February 15, 2001) Abstract Dynamics and energetics of the long-period ocean tides are investigated using a global barotropic ocean model. Estimated oceanic Qs of the long-period tides are about 3, which show that the ocean is heavily damped system. Some far-reaching tidal energy fluxes, however, exist. Equatorial eastward flux from the coast of South Africa to the Pacific especially stands out. LFrom the point of view of wave dynam ics, contrary to the tidal energy flux in the tropics, wave's energy propagates in the westward direction. With the relation between the energy flux of wave and group ve locity, the westward direction shows that the energy flux corresponds to long Rossby wave. Moreover, this relation clearly shows existence of short Rossby waves in the mid latitudes. LFrom the point of view of planetary scale dynamics, zonally averages of dy namic tide and tidal currents show existence of global non-equilibrium response, which is similar to a particular solution of constant depth ocean. The global response may corresponds to the deviation from the equilibrium tide in zonally averaged admittance, which is found in the analysis of altimeter data. 1. Introduction Though the ocean is heavily damped system for the long-period tides, non-equilibrium features can be found. Short Rossby wave (Wunsch,1967; Carton, 1983), long Rossby wave (Kantha et al., 1998) and Kelvin-like gravity wave (Miller et al., 1993) are proposed to be candidates for causes of the non-equilibrium features. However, where these waves exist is not clearly shown. This paper uses dynamics and energetics to determine the type and location of these waves that contribute to the non-equilibrium features of the long-period ocean tides. We also show existence of global response that is similar to O'Conner's (1992) particular solution. 2. Equations for Energetics and Dynamics We used solution of our constructed barotropic ocean model, of which grid size is half degree and computational method is finite difference method. Further details of the model can be referred from another paper in this proceedings (Takanezawa et al., 2001). For the followingarguments, we will show some equations for energetics and dynamics. *now at Faculty of Science, Kagoshima University, 1-21-35, Korimoto, Kagoshima-shi, Kagoshima-ken 890-0065, Tel/Fax: +81-99-285-8960, E-mail: [email protected] 552 Takashi Takanezawa, Koji Matsumoto, Masatsugu Ooe and Isao Naito An equation of energy balance for a barotropic ocean model can be expressed as follows. •¬(PE+KE)+‡™h•EP=RT+RD+RC (1) KE=phu2/2: kinetic energy, PE = pgƒÄ2/2: potential energy P=pg• (hƒÄu): tidal energy flux RT=pghu• ‡™h(ƒÅ+ƒÄ)=pgƒÅ(aƒÄ/at)+pgƒÄ(aƒÄ/at): rate of tidal work RC=phu• (f•~u): rate of work by Coriolis force (theoretically zero but some value remains because of finite grid size of model) RD = phu• F: rate of dissipation p: density of sea water, h: ocean depth u: tidal current, g: gravity accelerationƒÄ : tidal height, ƒÅ: primary tide generating potential esecondary tide generating potential (loading and self-attraction of sea water) F: friction (bottom friction and eddy viscosity in our model) f : Coriolis force, ‡™h: horizontal differential Integrating over the whole ocean and/or averaging over one tidal period give following equations. •¬(<KE>)+<PE>)=<RT>+<RD>+<RC>(3) < RT>+<RD>+<RC>=0 (4) where <> and -mean integrations over the whole ocean and averaging over one tidal period, respectively. Q-value of the ocean to the tidal force is conventionally defined as follows. Q = 2ƒÎE/‡™E (5) E=<[ph(u20+v20)+pgƒÄ20]/4>: mean energy of system ‡™ E=<RT>• T: energy loss per one tidal period u0, v0: amplitudes of eastward and northward tidal current velocitiesƒÄ0 : amplitude of tidal height, T: tidal period In the limit of linearity, the ocean tides can be represented by two kinds of expressions (Wunsch et al., 1997). ƒÄ =(equilibrium)+‡”nan(normalmode)n(6) ƒÄ =(particularsolution)+(homogenoussolution)(7) Wunsch et al. argued that superposing normal modes is mathematically valid but is not preferable to obtain the long-period ocean tides since the ocean is heavily damped system for the long-period tides and many spatially complicated modes would exist. Then they derived the Laplace's tidal equations directly with spectral element ocean model. However, the expression by normal modes is useful for interpreting the dynamics of non-equilibrium features in the case where the normal modes are not overlapped spatially or only the one of modes predominate. In such a case, since nonlinearity of energy with tidal height can be Non-equilibrium Characteristics of the Long-Period Ocean Tides 553 neglected, we can use wave's energy to determine the type of wave . Hence, we will define potential and kinetic energies of wave and energy flux of wave as follows. PEw=pg(ƒÄ-ƒÅ-ƒÄ)2/2 (8) KEw=phu2/2(9) Pw=pgh(ƒÄ-ƒÅ-ƒÄ)u(10) The definition of potential energy of wave seems to be doubtful at a glance , but it is valid in consideration that tidal currents of long-period ocean tides are close to the geostrophic flow. Here, we also define (ƒÄ-ƒÅ-ƒÄ) as dynamic tide following Miller et al . (1993). The energy flux of wave is related with group velocity by a well-known relation (e .g., Gill, 1982; Pedlosky, 1987), Pw=EwCg(11) Ew=PEw+KEw: mean energy density Cg: group velocity of wave Since the direction of group velocity depends on the type of wave, that of energy flux of wave can be used to determine the type of wave. On the second expression (eq.7), O'Connor (1992, 1995) obtained the particular solution for constant depth ocean and homogeneous solutions for meridional bounded ocean. His particular solution can express tidal currents simpler than Hough's function can. In this paper, we will use only his particular solution for discussion on global non-equilibrium response. Table 1. Oceanic Q for long-period tide. 3. Results and Discussion We show the Q-values of ocean to the long-period tides in Table 1. These values are about 3 except for Ssa, which show that the ocean is heavily damped system for the long- period tides. The Q-value of Ssa is very larger than those of other constituents, but it doesn't mean larger difference from the equilibrium or existence of problem on model. This value is due to small dissipation, and in the case of complete equilibrium no tidal current exists and hence the Q-value becomes infinity. Figure 1 shows divergence of Mf tidal energy flux and flux itself. Complicated distri bution of the divergence is due to strong effect of that of the rate of tidal work. Positive area means that the moon or sun work on the ocean, and negative area means opposite situation. The distribution of divergence suggests that the tidal energy hardly propagate far away. However, in Figure lb some large scale tidal energy fluxes, especially far-reaching tidal energy flux from off the Africa to the East Pacific Rise can be found. To know what kinds of waves correspond to these tidal energy fluxes, we use the energy flux of wave defined , 554 Takashi Takanezawa, Koji Matsumoto, Masatsugu Ooe and Isao Naito Fig.1. Mf tidal energy flux and its divergence. Fig.2. Energy flux of wave and group velocity of Mf tide. Fig.3. Energy flux of waves of Mtm and Mm tides. Non-equilibrium Characteristics of the Long-Period Ocean Tides 555 Fig.4. Contour of f/H (f:Coriolis parameter; H:ocean depth) . Contour interval= 10-8m-1s-1. Fig.5. Energy flux of wave of Mf tide in the case of excluding the Arctic Ocean . Fig.6. Zonal average of Mf dynamic tide and tidal velocities. The solid lines mean the value of our model and the dotted lines mean O'Connor's particular solution. 556 Takashi Takanezawa, Koji Matsumoto, Masatsugu Ooe and Isao Naito by eq.(10) (Figure 2a). In the tropics, contrary to the tidal energy flux, which stretches over the Indian Sea and Pacific Ocean and propagates eastward, the energy flux of wave is limited in the Pacific Ocean and propagates westward. This westward direction of the propagation means that the corresponding wave is long Rossby wave. Figure 2b shows that the group velocity obtained by the relation eq.(11) has reasonable value for Rossby wave. A similar westward energy flux of wave can be found in Mm constituent but cannot be found in Mtm (Figure 3). Also eastward fluxes in the mid-latitudes of North Pacific Ocean are found in Mf and Mm constituents. They are considered to correspond to short Rossby waves since they propagate eastward and attenuates as the tidal period becomes longer. This tendency of the attenuation is predicted by Carton (1983). Also fluxes in the Southern Pacific Ocean should be short Rossby waves since they propagate along the contours of f/H (Figure 4). In the Atlantic Ocean, Kelvin-likewave propagations can be found. These waves are estimated to be excited in the Arctic Ocean by comparison with the flux of a model that is run with the Arctic Ocean excluded (Figure 5).
Load more

Recommended publications
  • Baroclinic Instability, Lecture 19
    19. Baroclinic Instability In two-dimensional barotropic flow, there is an exact relationship between mass 2 streamfunction ψ and the conserved quantity, vorticity (η)given by η = ∇ ψ.The evolution of the conserved variable η in turn depends only on the spatial distribution of η andonthe flow, whichisd erivable fromψ and thus, by inverting the elliptic relation, from η itself. This strongly constrains the flow evolution and allows one to think about the flow by following η around and inverting its distribution to get the flow. In three-dimensional flow, the vorticity is a vector and is not in general con­ served. The appropriate conserved variable is the potential vorticity, but this is not in general invertible to find the flow, unless other constraints are provided. One such constraint is geostrophy, and a simple starting point is the set of quasi-geostrophic equations which yield the conserved and invertible quantity qp, the pseudo-potential vorticity. The same dynamical processes that yield stable and unstable Rossby waves in two-dimensional flow are responsible for waves and instability in three-dimensional baroclinic flow, though unlike the barotropic 2-D case, the three-dimensional dy­ namics depends on at least an approximate balance between the mass and flow fields. 97 Figure 19.1 a. The Eady model Perhaps the simplest example of an instability arising from the interaction of Rossby waves in a baroclinic flow is provided by the Eady Model, named after the British mathematician Eric Eady, who published his results in 1949. The equilibrium flow in Eady’s idealization is illustrated in Figure 19.1.
    [Show full text]
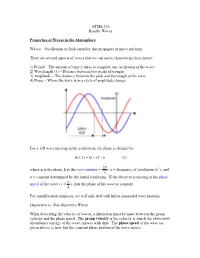
  • ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves
    ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves – Oscillations in field variables that propagate in space and time. There are several aspects of waves that we can use to characterize their nature: 1) Period – The amount of time it takes to complete one oscillation of the wave\ 2) Wavelength (λ) – Distance between two peaks of troughs 3) Amplitude – The distance between the peak and the trough of the wave 4) Phase – Where the wave is in a cycle of amplitude change For a 1-D wave moving in the x-direction, the phase is defined by: φ ),( = −υtkxtx − α (1) 2π where φ is the phase, k is the wave number = , υ = frequency of oscillation (s-1), and λ α = constant determined by the initial conditions. If the observer is moving at the phase υ speed of the wave ( c ≡ ), then the phase of the wave is constant. k For simplification purposes, we will only deal with linear sinusoidal wave motions. Dispersive vs. Non-dispersive Waves When describing the velocity of waves, a distinction must be made between the group velocity and the phase speed. The group velocity is the velocity at which the observable disturbance (energy of the wave) moves with time. The phase speed of the wave (as given above) is how fast the constant phase portion of the wave moves. A dispersive wave is one in which the pattern of the wave changes with time. In dispersive waves, the group velocity is usually different than the phase speed. A non- dispersive wave is one in which the patterns of the wave do not change with time as the wave propagates (“rigid” wave).
    [Show full text]
  • TTL Upwelling Driven by Equatorial Waves
    TTL Upwelling driven by Equatorial Waves L09804 LIUWhat drives the annual cycle in TTL upwelling? ET AL.: START OF WATER VAPOR AND CO TAPE RECORDERS L09804 Liu et al. (2007) Ortland, D. and M. J. Alexander, The residual mean circula8on in the TTL driven by tropical waves, JAS, (in review), 2013. Figure 1. (a) Seasonal variation of 10°N–10°S mean EOS MLS water vapor after dividing by the mean value at each level. (b) Seasonal variation of 10°N–10°S EOS MLS CO after dividing by the mean value at each level. represented in two principal ways. The first is by the area of [8]ConcentrationsofwatervaporandCOnearthe clouds with low infrared brightness temperatures [Gettelman tropical tropopause are available from retrievals of EOS et al.,2002;Massie et al.,2002;Liu et al.,2007].Thesecond MLS measurements [Livesey et al.,2005,2006].Monthly is by the area of radar echoes reaching the tropopause mean water vapor and CO mixing ratios at 146 hPa and [Alcala and Dessler,2002;Liu and Zipser, 2005]. In this 100 hPa in the 10°N–10°Sand10° longitude boxes are study, we examine the areas of clouds that have TRMM calculated from one full year (2005) of version 1.5 MLS Visible and Infrared Scanner (VIRS) 10.8 mmbrightness retrievals. In this work, all MLS data are processed with temperatures colder than 210 K, and the area of 20 dBZ requirements described by Livesey et al. [2005]. Tropopause echoes at 14 km measured by the TRMM Precipitation temperature is averaged from the 2.5° resolution NCEP Radar (PR).
    [Show full text]
  • Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect Along Western Boundaries with Bottom Topography and Dissipation
    JANUARY 2020 W I S E E T A L . 217 Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect along Western Boundaries with Bottom Topography and Dissipation ANTHONY WISE National Oceanography Centre, and Department of Earth, Ocean and Ecological Sciences, University of Liverpool, Liverpool, United Kingdom CHRIS W. HUGHES Department of Earth, Ocean and Ecological Sciences, University of Liverpool, and National Oceanography Centre, Liverpool, United Kingdom JEFF A. POLTON AND JOHN M. HUTHNANCE National Oceanography Centre, Liverpool, United Kingdom (Manuscript received 5 April 2019, in final form 29 October 2019) ABSTRACT Coastal trapped waves (CTWs) carry the ocean’s response to changes in forcing along boundaries and are important mechanisms in the context of coastal sea level and the meridional overturning circulation. Motivated by the western boundary response to high-latitude and open-ocean variability, we use a linear, barotropic model to investigate how the latitude dependence of the Coriolis parameter (b effect), bottom topography, and bottom friction modify the evolution of western boundary CTWs and sea level. For annual and longer period waves, the boundary response is characterized by modified shelf waves and a new class of leaky slope waves that propagate alongshore, typically at an order slower than shelf waves, and radiate short Rossby waves into the interior. Energy is not only transmitted equatorward along the slope, but also eastward into the interior, leading to the dissipation of energy locally and offshore. The b effectandfrictionresultinshelfandslope waves that decay alongshore in the direction of the equator, decreasing the extent to which high-latitude variability affects lower latitudes and increasing the penetration of open-ocean variability onto the shelf—narrower conti- nental shelves and larger friction coefficients increase this penetration.
    [Show full text]
  • The Counter-Propagating Rossby-Wave Perspective on Baroclinic Instability
    Q. J. R. Meteorol. Soc. (2005), 131, pp. 1393–1424 doi: 10.1256/qj.04.22 The counter-propagating Rossby-wave perspective on baroclinic instability. Part III: Primitive-equation disturbances on the sphere 1∗ 2 1 3 CORE By J. METHVEN , E. HEIFETZ , B. J. HOSKINS and C. H. BISHOPMetadata, citation and similar papers at core.ac.uk 1 Provided by Central Archive at the University of Reading University of Reading, UK 2Tel-Aviv University, Israel 3Naval Research Laboratories/UCAR, Monterey, USA (Received 16 February 2004; revised 28 September 2004) SUMMARY Baroclinic instability of perturbations described by the linearized primitive equations, growing on steady zonal jets on the sphere, can be understood in terms of the interaction of pairs of counter-propagating Rossby waves (CRWs). The CRWs can be viewed as the basic components of the dynamical system where the Hamil- tonian is the pseudoenergy and each CRW has a zonal coordinate and pseudomomentum. The theory holds for adiabatic frictionless flow to the extent that truncated forms of pseudomomentum and pseudoenergy are globally conserved. These forms focus attention on Rossby wave activity. Normal mode (NM) dispersion relations for realistic jets are explained in terms of the two CRWs associated with each unstable NM pair. Although derived from the NMs, CRWs have the conceptual advantage that their structure is zonally untilted, and can be anticipated given only the basic state. Moreover, their zonal propagation, phase-locking and mutual interaction can all be understood by ‘PV-thinking’ applied at only two ‘home-bases’— potential vorticity (PV) anomalies at one home-base induce circulation anomalies, both locally and at the other home-base, which in turn can advect the PV gradient and modify PV anomalies there.
    [Show full text]
  • MAST602: Introduction to Physical Oceanography (Andreas Münchow) (Closed Book In-Class Rossby Wave Exercise, Oct.-21, 2008)
    MAST602: Introduction to Physical Oceanography (Andreas Münchow) (Closed book in-class Rossby Wave Exercise, Oct.-21, 2008) In a series of papers published in the 1930ies Carl-Gustaf Rossby introduced a strange new wave form whose existence has not been confirmed observationally until the late 1990ies. A debate is presently raging if and how these waves may impact ecosystems in the ocean, e.g., “Killworth et al., 2003: Physical and biological mechanisms for planetary waves observed in satellite-derived chlorophyll, J. Geophys. Res.” and “Dandonneau et al., 2003: Oceanic Rossby waves acting as a “Hay Rake” for ecosystem floating by- products, Science” as well as a flurry of comments generated by these papers. These peculiar waves originate from a linear balance between local acceleration, Coriolis acceleration, and pressure gradients as well as continuity of mass, that is, East-west momentum balance: ∂u/∂t – fv = -g ∂η/∂x North-south momentum balance: ∂v/∂t + fu = -g ∂η/∂y Continuity: ∂η/∂t + H (∂u/∂x+∂v/∂y) = 0 where the Coriolis parameter f = 2 Ω sin(latitude) is no longer a constant, but is approximated locally as f ≈ f0 + βy. The rotational rate of the earth is Ω=2π/day and at the -4 -1 -11 -1 -1 latitude of Lewes, DE (39N), f0~0.9×10 s and β~2×10 m s . A number of peculiar properties can be inferred from its dispersion relation: σ = − β κ / (κ2+l2+R-2) where σ is the wave frequency, κ is the wave number in the east-west direction, l is the wave number in the north-south direction, β is a constant (the so-called beta-parameter 1/2 that incorporates Coriolis effects that changes with latitude), and R=(g’H) /f0 is a constant (the so-called Rossby radius of deformation, the same as the lateral decay scale of the Kelvin wave, where g’~9.81×10-3m/s2 is the constant of “reduced” gravity, and H~1000 m is the depth of the pycnocline (density interface).
    [Show full text]
  • El Niño: the Ocean in Climate El Niño: the Ocean in Climate
    El Niño: The ocean in climate We live in the atmosphere: where is it sensitive to the ocean? ➞ The tropics! El Niño is the most spectacular short-term climate oscillation. It affects weather around the world, and illustrates the many aspects of O-A interaction Most of the poleward heat transport is by the atmosphere First hint that this may all be myth comes from using observations to estimate atmosphere and ocean(except heat in the tropics) transports Ocean and atmosphere heat transports Heat transport is poleward in &'()*('&+,-.,/01,2%""34,-5.67/.-5,89:,;9:.<=/:>,<-/.,.:/;5?9:.5 # both ocean and atmosphere: )D(B,E('1,F&G (DGCH,E('1,F&G )D(B,E('1,ID(F) Atmosphere (DGCH,E('1,ID(F) The role of the O-A system is $ Net radiation at Atmosphere (line) to move excess heat from the top of atmosphere tropics to the poles, where it Ocean (Dashed) Ocean = divergence of % is radiated to space. (AHT + OHT) " BC Net radiation Northward transport (PW) !% from satellites, AHT from weather obs !$ and models, OHT from residual Trenberth et al (2001) !# 80°S!!" 60°S!#" 40°S!$" 20°S!%" 0°" 20°N%" 40°N$" 60°N#" 80°N!" @/.6.A>- Most of the poleward transport occurs in mid-latitude winter storms near 40°S/N. Only in the tropics is the ocean really important. Much recent interest in the “global conveyor belt” But the timescales are very slow Does the Gulf Stream warm Europe? An example of the (largely) passive effect of the ocean Why is Ireland warmer than Labrador in winter? Because of need to conserve angular momentum, Rockies force a stationary wave in the westerlies with northerly flow (cooling) over eastern N.
    [Show full text]
  • Topographic Rossby Waves in the Arctic Ocean's Beaufort Gyre
    Journal of Geophysical Research: Oceans RESEARCH ARTICLE Topographic Rossby Waves in the Arctic Ocean’s Beaufort Gyre 10.1029/2018JC014233 Bowen Zhao1 and Mary-Louise Timmermans1 Special Section: Forum for Arctic Modeling 1Department of Geology & Geophysics, Yale University, New Haven, CT, USA and Observational Synthesis (FAMOS) 2: Beaufort Gyre phenomenon Abstract A 5-year long time series of temperature and horizontal velocity in the Arctic Ocean’s Key Points: Beaufort Gyre is analyzed with the aim of understanding the mechanism driving the observed variability • Beaufort Gyre mooring on timescales of tens of days (i.e., subinertial). We employ a coherency/phase analysis on the temperature measurements of velocity and and horizontal velocity signals, which indicates that subinertial temperature variations arise from vertical temperature are analyzed for subinertial signal excursions of the water column that are driven by horizontal motions across the sloping seafloor. The • Observations are consistent vertical displacements of the water column (recorded by the temperature signal) show a bottom-intensified with topographic Rossby waves signature (i.e., decay toward the surface), while horizontal velocity anomalies are approximately barotropic propagating on sloping seafloor • Topographic Rossby waves play a role below the main halocline. We show that the different characteristics in vertical and horizontal velocities are in Beaufort Gyre stabilization consistent with topographic Rossby wave theory in the limit of weak vertical decay. In essence, a linearly decaying vertical velocity profile implies that the whole water column is stretched/squashed uniformly with Correspondence to: depth when water moves horizontally across the bottom slope. Thus, for the uniform stratification of the B.
    [Show full text]
  • Lecture 5: the Spectrum of Free Waves Possible Along Coasts
    Lecture 5: The Spectrum of Free Waves Possible along Coasts Myrl Hendershott 1 Introduction In this lecture we discuss the spectrum of free waves that are possible along the straight coast in shallow water approximation. 2 Linearized shallow water equations The linearized shallow water equations(LSW) are u fv = gζ ; (1) t − − x v + fu = gζ ; (2) t − y ζt + (uD)x + (vD)y = 0: (3) where D; η are depth and free surface elevations respectively. 3 Kelvin Waves Kelvin waves require the support of a lateral boundary and it occurs in the ocean where it can travel along coastlines. Consider the case when u = 0 in the linearized shallow water equations with constant depth. In this case we have that the Coriolis force in the offshore direction is balanced by the pressure gradient towards the coast and the acceleration in the Longshore direction is gravitational. Substituting u = 0 in equation (1) through (3) (assuming constant depth D) gives fv = gζx; (4) v = gζ ; (5) t − y ζt + Dvy = 0; (6) eliminating ζ between equation (4) through equation (6) gives vtt = (gD)vyy: (7) The general wave solution can be written as v = V (x; y + ct) + V (x; y ct); (8) 1 2 − 63 2 where c = gD and V1; V2 are arbitrary functions. Now note that ζ satisfies ζtt = (gD)ζyy: (9) Hence we can try ζ = AV (x; y + ct) + BV (x; y ct). From equation (4) or equation (5) 1 2 − we get A = H=g , b = H=g. V and V can be determined as follows.
    [Show full text]
  • Detection of Rossby Wave Breaking and Its Response to Shifts of the Midlatitude Jet with Climate Change
    JOURNAL OF GEOPHYSICAL RESEARCH, VOL. ???, XXXX, DOI:10.1029/, Detection of Rossby wave breaking and its response to shifts of the midlatitude jet with climate change 1 1 Elizabeth A. Barnes and Dennis L. Hartmann Elizabeth A. Barnes, Department of Atmospheric Sciences, University Washington, Box 351640, Seattle, WA 98195. ([email protected]) Dennis L. Hartmann, Department of Atmospheric Sciences, University Washington, Box 351640, Seattle, WA 98195. ([email protected]) 1Department of Atmospheric Science, University of Washington, Seattle, Washington, USA. D R A F T March 5, 2012, 10:18am D R A F T X-2 BARNES AND HARTMANN: WAVE BREAKING AND CLIMATE CHANGE Abstract. A Rossby wave breaking identification method is presented which searches for overturning of absolute vorticity contours on pressure sur- faces. The results are compared to those from an analysis of isentropic po- tential vorticity, and it is demonstrated that both yield similar wave break- ing distributions. As absolute vorticity is easily obtained from most model output, we present wave breaking frequency distributions from the ERA-Interim data set, thirteen general circulation models (GCMs) and a barotropic model. We demonstrate that a poleward shift of the Southern Hemisphere midlat- itude jet is accompanied by a decrease in poleward wave breaking in both the barotropic model and all GCMs across three climate forcing scenarios. In addition, it is shown that while anticyclonic wave breaking shifts poleward with the jet, cyclonic wave breaking shifts less than half as much and reaches a poleward limit near 60 degrees S. Comparison of the observed distribution of Southern Hemisphere wave breaking with those from the GCMs suggests that wave breaking on the poleward flank of the jet has already reached its poleward limit and will likely become less frequent if the jet migrates any further poleward with climate change.
    [Show full text]
  • Geophysics Fluid Dynamics (ESS228)
    Geophysics Fluid Dynamics (ESS228) . Course Time Lectures: Tu, Th 09:30-10:50 Discussion: 3315 Croul Hall . Text Book J. R. Holton, "An introduction to Dynamic Meteorology", Academic Press (Ch. 1, 2, 3, 4, 6, 8, 11). Adrian E. Gill, "Atmosphere-Ocean Dynamics", Academic Press (Ch. 5, 6, 7, 8, 9, 10, 11, 12). Grade Homework (30%), Midterm (35%), Final (35%) . Homework Issued and due every Thursday ESS227 Prof. Jin-Yi Yu Syllabus ESS227 Prof. Jin-Yi Yu Dynamics and Kinematics • Kinematics: The term kinematics means motion. Kinematics is the study of motion without regard for the cause. • Dynamics: On the other hand, dynamics is the study of the causes of motion. This course discusses the physical laws that govern atmosphere/ocean motions. ESS228 Prof. Jin-Yi Yu Geophysical Fluid Dynamics the study of the causes of motion causes: solar radiation competes with gravity distributions of T and motions governed by conservation laws ESS227 Prof. Jin-Yi Yu Newton’s 2nd Law of Motion Newton’s 2nd Law of Momentum = absolute velocity viewed in an inertial system = rate of change of Ua following the motion in an inertial system • The conservation law for momentum (Newton’s second law of motion) relates the rate of change of the absolute momentum following the motion in an inertial reference frame to the sum of the forces acting on the fluid. ESS228 Prof. Jin-Yi Yu Conservation of Mass • The mathematical relationship that expresses conservation of mass for a fluid is called the continuity equation. (mass divergence form) (velocity divergence form) ESS228 Prof. Jin-Yi Yu The First Law of Thermodynamics • This law states that (1) heat is a form of energy that (2) its conversion into other forms of energy is such that total energy is conserved.
    [Show full text]
  • Influence of Rossby Waves on Primary Production from a Coupled Physical
    Ocean Sci., 4, 199–213, 2008 www.ocean-sci.net/4/199/2008/ Ocean Science © Author(s) 2008. This work is distributed under the Creative Commons Attribution 3.0 License. Influence of Rossby waves on primary production from a coupled physical-biogeochemical model in the North Atlantic Ocean G. Charria1,2, I. Dadou1, P. Cipollini2, M. Drevillon´ 3, and V. Garc¸on1 1Laboratoire d’Etudes en Geophysique´ et Oceanographie´ Spatiales, UMR5566/CNRS, Toulouse, France 2National Oceanography Centre, Southampton, United Kingdom 3CERFACS, MERCATOR-Ocean,´ Toulouse, France Received: 30 October 2007 – Published in Ocean Sci. Discuss.: 29 November 2007 Revised: 9 July 2008 – Accepted: 1 August 2008 – Published: 1 September 2008 Abstract. Rossby waves appear to have a clear signature on actions. Based on remotely sensed data and/or coupled surface chlorophyll concentrations which can be explained physical/biogeochemical modelling, several studies inves- by a combination of vertical and horizontal mechanisms. In tigated the coupled physical/biogeochemical mechanisms this study, we investigate the role of the different physical which might be involved (e.g. Charria et al., 2003, 2006a; processes in the north Atlantic to explain the surface chloro- Killworth et al., 2004). Three main processes were sug- phyll signatures and the consequences on primary produc- gested: (1) the upwelling mechanism associated with nutri- tion, using a 3-D coupled physical/biogeochemical model for ent injection (Cipollini et al., 2001; Uz et al., 2001; Siegel, the year 1998. 2001), (2) the uplifting of a deep chlorophyll maximum to- The analysis at 20 given latitudes, mainly located in the wards the surface (Cipollini et al., 2001; Kawamiya and Os- subtropical gyre, where Rossby waves are strongly correlated chlies, 2001; Charria et al., 2003), and (3) the meridional with a surface chlorophyll signature, shows the important advection of chlorophyll by geostrophic currents associated contribution of horizontal advection and of vertical advec- with baroclinic Rossby waves (Killworth et al., 2004).
    [Show full text]