Baroclinic Instability, Lecture 19
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Meteotsunami Generation, Amplification and Occurrence in North-West Europe
University of Liverpool Doctoral Thesis Meteotsunami generation, amplification and occurrence in north-west Europe Thesis submitted in accordance with the requirements of the University of Liverpool for the degree of Doctor in Philosophy by David Alan Williams November 2019 ii Declaration of Authorship I declare that this thesis titled “Meteotsunami generation, amplification and occurrence in north-west Europe” and the work presented in it are my own work. The material contained in the thesis has not been presented, nor is currently being presented, either wholly or in part, for any other degree or qualification. Signed Date David A Williams iii iv Meteotsunami generation, amplification and occurrence in north-west Europe David A Williams Abstract Meteotsunamis are atmospherically generated tsunamis with characteristics similar to all other tsunamis, and periods between 2–120 minutes. They are associated with strong currents and may unexpectedly cause large floods. Of highest concern, meteotsunamis have injured and killed people in several locations around the world. To date, a few meteotsunamis have been identified in north-west Europe. This thesis aims to increase the preparedness for meteotsunami occurrences in north-west Europe, by understanding how, when and where meteotsunamis are generated. A summer-time meteotsunami in the English Channel is studied, and its generation is examined through hydrodynamic numerical simulations. Simple representations of the atmospheric system are used, and termed synthetic modelling. The identified meteotsunami was partly generated by an atmospheric system moving at the shallow- water wave speed, a mechanism called Proudman resonance. Wave heights in the English Channel are also sensitive to the tide, because tidal currents change the shallow-water wave speed. -

Destructive Meteotsunamis Along the Eastern Adriatic Coast: Overview
Physics and Chemistry of the Earth 34 (2009) 904–917 Contents lists available at ScienceDirect Physics and Chemistry of the Earth journal homepage: www.elsevier.com/locate/pce Destructive meteotsunamis along the eastern Adriatic coast: Overview Ivica Vilibic´ *, Jadranka Šepic´ Institute of Oceanography and Fisheries, Šetalište I. Meštrovic´a 63, 21000 Split, Croatia article info abstract Article history: The paper overviews meteotsunami events documented in the Adriatic Sea in the last several decades, by Received 10 December 2008 using available eyewitness reports, documented literature, and atmospheric sounding and meteorologi- Accepted 24 August 2009 cal reanalysis data available on the web. The source of all documented Adriatic meteotsunamis was Available online 28 August 2009 examined by assessing the underlying synoptic conditions. It is found that travelling atmospheric distur- bances which generate the Adriatic meteotsunamis generally appear under atmospheric conditions doc- Keywords: umented also for the Balearic meteotsunamis (rissagas). These atmospheric disturbances are commonly Meteotsunami generated by a flow over the mountain ridges (Apennines), and keep their energy through the wave-duct Atmospheric disturbance mechanism while propagating over a long distance below the unstable layer in the mid-troposphere. Resonance Long ocean waves However, the Adriatic meteotsunamis may also be generated by a moving convective storm or gravity Adriatic Sea wave system coupled in the wave-CISK (Conditional Instability of the Second Kind) manner, not docu- mented at other world meteotsunami hot spots. The travelling atmospheric disturbance is resonantly pumping the energy through the Proudman resonance over the wide Adriatic shelf, but other resonances (Greenspan, shelf) are also presumably influencing the strength of the meteotsunami waves, especially in the middle Adriatic, full of elongated islands and with a sloping bathymetry. -

A High-Amplitude Atmospheric Inertia–Gravity Wave-Induced
A high-amplitude atmospheric inertia– gravity wave-induced meteotsunami in Lake Michigan Eric J. Anderson & Greg E. Mann Natural Hazards ISSN 0921-030X Nat Hazards DOI 10.1007/s11069-020-04195-2 1 23 Your article is protected by copyright and all rights are held exclusively by This is a U.S. Government work and not under copyright protection in the US; foreign copyright protection may apply. This e-offprint is for personal use only and shall not be self- archived in electronic repositories. If you wish to self-archive your article, please use the accepted manuscript version for posting on your own website. You may further deposit the accepted manuscript version in any repository, provided it is only made publicly available 12 months after official publication or later and provided acknowledgement is given to the original source of publication and a link is inserted to the published article on Springer's website. The link must be accompanied by the following text: "The final publication is available at link.springer.com”. 1 23 Author's personal copy Natural Hazards https://doi.org/10.1007/s11069-020-04195-2 ORIGINAL PAPER A high‑amplitude atmospheric inertia–gravity wave‑induced meteotsunami in Lake Michigan Eric J. Anderson1 · Greg E. Mann2 Received: 1 February 2020 / Accepted: 17 July 2020 © This is a U.S. Government work and not under copyright protection in the US; foreign copyright protection may apply 2020 Abstract On Friday, April 13, 2018, a high-amplitude atmospheric inertia–gravity wave packet with surface pressure perturbations exceeding 10 mbar crossed the lake at a propagation speed that neared the long-wave gravity speed of the lake, likely producing Proudman resonance. -

Infragravity Wave Energy Partitioning in the Surf Zone in Response to Wind-Sea and Swell Forcing
Journal of Marine Science and Engineering Article Infragravity Wave Energy Partitioning in the Surf Zone in Response to Wind-Sea and Swell Forcing Stephanie Contardo 1,*, Graham Symonds 2, Laura E. Segura 3, Ryan J. Lowe 4 and Jeff E. Hansen 2 1 CSIRO Oceans and Atmosphere, Crawley 6009, Australia 2 Faculty of Science, School of Earth Sciences, The University of Western Australia, Crawley 6009, Australia; [email protected] (G.S.); jeff[email protected] (J.E.H.) 3 Departamento de Física, Universidad Nacional, Heredia 3000, Costa Rica; [email protected] 4 Faculty of Engineering and Mathematical Sciences, Oceans Graduate School, The University of Western Australia, Crawley 6009, Australia; [email protected] * Correspondence: [email protected] Received: 18 September 2019; Accepted: 23 October 2019; Published: 28 October 2019 Abstract: An alongshore array of pressure sensors and a cross-shore array of current velocity and pressure sensors were deployed on a barred beach in southwestern Australia to estimate the relative response of edge waves and leaky waves to variable incident wind wave conditions. The strong sea 1 breeze cycle at the study site (wind speeds frequently > 10 m s− ) produced diurnal variations in the peak frequency of the incident waves, with wind sea conditions (periods 2 to 8 s) dominating during the peak of the sea breeze and swell (periods 8 to 20 s) dominating during times of low wind. We observed that edge wave modes and their frequency distribution varied with the frequency of the short-wave forcing (swell or wind-sea) and edge waves were more energetic than leaky waves for the duration of the 10-day experiment. -
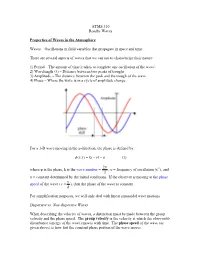
ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves
ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves – Oscillations in field variables that propagate in space and time. There are several aspects of waves that we can use to characterize their nature: 1) Period – The amount of time it takes to complete one oscillation of the wave\ 2) Wavelength (λ) – Distance between two peaks of troughs 3) Amplitude – The distance between the peak and the trough of the wave 4) Phase – Where the wave is in a cycle of amplitude change For a 1-D wave moving in the x-direction, the phase is defined by: φ ),( = −υtkxtx − α (1) 2π where φ is the phase, k is the wave number = , υ = frequency of oscillation (s-1), and λ α = constant determined by the initial conditions. If the observer is moving at the phase υ speed of the wave ( c ≡ ), then the phase of the wave is constant. k For simplification purposes, we will only deal with linear sinusoidal wave motions. Dispersive vs. Non-dispersive Waves When describing the velocity of waves, a distinction must be made between the group velocity and the phase speed. The group velocity is the velocity at which the observable disturbance (energy of the wave) moves with time. The phase speed of the wave (as given above) is how fast the constant phase portion of the wave moves. A dispersive wave is one in which the pattern of the wave changes with time. In dispersive waves, the group velocity is usually different than the phase speed. A non- dispersive wave is one in which the patterns of the wave do not change with time as the wave propagates (“rigid” wave). -

TTL Upwelling Driven by Equatorial Waves
TTL Upwelling driven by Equatorial Waves L09804 LIUWhat drives the annual cycle in TTL upwelling? ET AL.: START OF WATER VAPOR AND CO TAPE RECORDERS L09804 Liu et al. (2007) Ortland, D. and M. J. Alexander, The residual mean circula8on in the TTL driven by tropical waves, JAS, (in review), 2013. Figure 1. (a) Seasonal variation of 10°N–10°S mean EOS MLS water vapor after dividing by the mean value at each level. (b) Seasonal variation of 10°N–10°S EOS MLS CO after dividing by the mean value at each level. represented in two principal ways. The first is by the area of [8]ConcentrationsofwatervaporandCOnearthe clouds with low infrared brightness temperatures [Gettelman tropical tropopause are available from retrievals of EOS et al.,2002;Massie et al.,2002;Liu et al.,2007].Thesecond MLS measurements [Livesey et al.,2005,2006].Monthly is by the area of radar echoes reaching the tropopause mean water vapor and CO mixing ratios at 146 hPa and [Alcala and Dessler,2002;Liu and Zipser, 2005]. In this 100 hPa in the 10°N–10°Sand10° longitude boxes are study, we examine the areas of clouds that have TRMM calculated from one full year (2005) of version 1.5 MLS Visible and Infrared Scanner (VIRS) 10.8 mmbrightness retrievals. In this work, all MLS data are processed with temperatures colder than 210 K, and the area of 20 dBZ requirements described by Livesey et al. [2005]. Tropopause echoes at 14 km measured by the TRMM Precipitation temperature is averaged from the 2.5° resolution NCEP Radar (PR). -

Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect Along Western Boundaries with Bottom Topography and Dissipation
JANUARY 2020 W I S E E T A L . 217 Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect along Western Boundaries with Bottom Topography and Dissipation ANTHONY WISE National Oceanography Centre, and Department of Earth, Ocean and Ecological Sciences, University of Liverpool, Liverpool, United Kingdom CHRIS W. HUGHES Department of Earth, Ocean and Ecological Sciences, University of Liverpool, and National Oceanography Centre, Liverpool, United Kingdom JEFF A. POLTON AND JOHN M. HUTHNANCE National Oceanography Centre, Liverpool, United Kingdom (Manuscript received 5 April 2019, in final form 29 October 2019) ABSTRACT Coastal trapped waves (CTWs) carry the ocean’s response to changes in forcing along boundaries and are important mechanisms in the context of coastal sea level and the meridional overturning circulation. Motivated by the western boundary response to high-latitude and open-ocean variability, we use a linear, barotropic model to investigate how the latitude dependence of the Coriolis parameter (b effect), bottom topography, and bottom friction modify the evolution of western boundary CTWs and sea level. For annual and longer period waves, the boundary response is characterized by modified shelf waves and a new class of leaky slope waves that propagate alongshore, typically at an order slower than shelf waves, and radiate short Rossby waves into the interior. Energy is not only transmitted equatorward along the slope, but also eastward into the interior, leading to the dissipation of energy locally and offshore. The b effectandfrictionresultinshelfandslope waves that decay alongshore in the direction of the equator, decreasing the extent to which high-latitude variability affects lower latitudes and increasing the penetration of open-ocean variability onto the shelf—narrower conti- nental shelves and larger friction coefficients increase this penetration. -

The Life Cycle of Baroclinic Eddies in a Storm Track Environment
3498 JOURNAL OF THE ATMOSPHERIC SCIENCES VOLUME 57 The Life Cycle of Baroclinic Eddies in a Storm Track Environment ISIDORO ORLANSKI AND BRIAN GROSS Geophysical Fluid Dynamics Laboratory, Princeton, New Jersey (Manuscript received 15 April 1999, in ®nal form 1 March 2000) ABSTRACT The life cycle of baroclinic eddies in a controlled storm track environment has been examined by means of long model integrations on a hemisphere. A time-lagged regression that captures disturbances with large me- ridional velocities has been applied to the meteorological variables. This regressed solution is used to describe the life cycle of the baroclinic eddies. The eddies grow as expected by strong poleward heat ¯uxes at low levels in regions of strong surface baroclinicity at the entrance of the storm track, in a manner similar to that of Charney modes. As the eddies evolve into a nonlinear regime, they grow deeper by ¯uxing energy upward, and the characteristic westward tilt exhibited in the vorticity vanishes by rotating into a meridional tilt, in which the lower-level cyclonic vorticity center moves poleward and the upper-level center moves equatorward. This rather classical picture of baroclinic evolution is radically modi®ed by the simultaneous development of an upper-level eddy downstream of the principal eddy. The results suggest that this eddy is an integral part of a self-sustained system here named as a couplet, such that the upstream principal eddy in its evolution ¯uxes energy to the upper-level downstream eddy, whereas at lower levels the principal eddy receives energy ¯uxes from its downstream companion but grows primarily from baroclinic sources. -

The Counter-Propagating Rossby-Wave Perspective on Baroclinic Instability
Q. J. R. Meteorol. Soc. (2005), 131, pp. 1393–1424 doi: 10.1256/qj.04.22 The counter-propagating Rossby-wave perspective on baroclinic instability. Part III: Primitive-equation disturbances on the sphere 1∗ 2 1 3 CORE By J. METHVEN , E. HEIFETZ , B. J. HOSKINS and C. H. BISHOPMetadata, citation and similar papers at core.ac.uk 1 Provided by Central Archive at the University of Reading University of Reading, UK 2Tel-Aviv University, Israel 3Naval Research Laboratories/UCAR, Monterey, USA (Received 16 February 2004; revised 28 September 2004) SUMMARY Baroclinic instability of perturbations described by the linearized primitive equations, growing on steady zonal jets on the sphere, can be understood in terms of the interaction of pairs of counter-propagating Rossby waves (CRWs). The CRWs can be viewed as the basic components of the dynamical system where the Hamil- tonian is the pseudoenergy and each CRW has a zonal coordinate and pseudomomentum. The theory holds for adiabatic frictionless flow to the extent that truncated forms of pseudomomentum and pseudoenergy are globally conserved. These forms focus attention on Rossby wave activity. Normal mode (NM) dispersion relations for realistic jets are explained in terms of the two CRWs associated with each unstable NM pair. Although derived from the NMs, CRWs have the conceptual advantage that their structure is zonally untilted, and can be anticipated given only the basic state. Moreover, their zonal propagation, phase-locking and mutual interaction can all be understood by ‘PV-thinking’ applied at only two ‘home-bases’— potential vorticity (PV) anomalies at one home-base induce circulation anomalies, both locally and at the other home-base, which in turn can advect the PV gradient and modify PV anomalies there. -

MAST602: Introduction to Physical Oceanography (Andreas Münchow) (Closed Book In-Class Rossby Wave Exercise, Oct.-21, 2008)
MAST602: Introduction to Physical Oceanography (Andreas Münchow) (Closed book in-class Rossby Wave Exercise, Oct.-21, 2008) In a series of papers published in the 1930ies Carl-Gustaf Rossby introduced a strange new wave form whose existence has not been confirmed observationally until the late 1990ies. A debate is presently raging if and how these waves may impact ecosystems in the ocean, e.g., “Killworth et al., 2003: Physical and biological mechanisms for planetary waves observed in satellite-derived chlorophyll, J. Geophys. Res.” and “Dandonneau et al., 2003: Oceanic Rossby waves acting as a “Hay Rake” for ecosystem floating by- products, Science” as well as a flurry of comments generated by these papers. These peculiar waves originate from a linear balance between local acceleration, Coriolis acceleration, and pressure gradients as well as continuity of mass, that is, East-west momentum balance: ∂u/∂t – fv = -g ∂η/∂x North-south momentum balance: ∂v/∂t + fu = -g ∂η/∂y Continuity: ∂η/∂t + H (∂u/∂x+∂v/∂y) = 0 where the Coriolis parameter f = 2 Ω sin(latitude) is no longer a constant, but is approximated locally as f ≈ f0 + βy. The rotational rate of the earth is Ω=2π/day and at the -4 -1 -11 -1 -1 latitude of Lewes, DE (39N), f0~0.9×10 s and β~2×10 m s . A number of peculiar properties can be inferred from its dispersion relation: σ = − β κ / (κ2+l2+R-2) where σ is the wave frequency, κ is the wave number in the east-west direction, l is the wave number in the north-south direction, β is a constant (the so-called beta-parameter 1/2 that incorporates Coriolis effects that changes with latitude), and R=(g’H) /f0 is a constant (the so-called Rossby radius of deformation, the same as the lateral decay scale of the Kelvin wave, where g’~9.81×10-3m/s2 is the constant of “reduced” gravity, and H~1000 m is the depth of the pycnocline (density interface). -

El Niño: the Ocean in Climate El Niño: the Ocean in Climate
El Niño: The ocean in climate We live in the atmosphere: where is it sensitive to the ocean? ➞ The tropics! El Niño is the most spectacular short-term climate oscillation. It affects weather around the world, and illustrates the many aspects of O-A interaction Most of the poleward heat transport is by the atmosphere First hint that this may all be myth comes from using observations to estimate atmosphere and ocean(except heat in the tropics) transports Ocean and atmosphere heat transports Heat transport is poleward in &'()*('&+,-.,/01,2%""34,-5.67/.-5,89:,;9:.<=/:>,<-/.,.:/;5?9:.5 # both ocean and atmosphere: )D(B,E('1,F&G (DGCH,E('1,F&G )D(B,E('1,ID(F) Atmosphere (DGCH,E('1,ID(F) The role of the O-A system is $ Net radiation at Atmosphere (line) to move excess heat from the top of atmosphere tropics to the poles, where it Ocean (Dashed) Ocean = divergence of % is radiated to space. (AHT + OHT) " BC Net radiation Northward transport (PW) !% from satellites, AHT from weather obs !$ and models, OHT from residual Trenberth et al (2001) !# 80°S!!" 60°S!#" 40°S!$" 20°S!%" 0°" 20°N%" 40°N$" 60°N#" 80°N!" @/.6.A>- Most of the poleward transport occurs in mid-latitude winter storms near 40°S/N. Only in the tropics is the ocean really important. Much recent interest in the “global conveyor belt” But the timescales are very slow Does the Gulf Stream warm Europe? An example of the (largely) passive effect of the ocean Why is Ireland warmer than Labrador in winter? Because of need to conserve angular momentum, Rockies force a stationary wave in the westerlies with northerly flow (cooling) over eastern N. -

Topographic Rossby Waves in the Arctic Ocean's Beaufort Gyre
Journal of Geophysical Research: Oceans RESEARCH ARTICLE Topographic Rossby Waves in the Arctic Ocean’s Beaufort Gyre 10.1029/2018JC014233 Bowen Zhao1 and Mary-Louise Timmermans1 Special Section: Forum for Arctic Modeling 1Department of Geology & Geophysics, Yale University, New Haven, CT, USA and Observational Synthesis (FAMOS) 2: Beaufort Gyre phenomenon Abstract A 5-year long time series of temperature and horizontal velocity in the Arctic Ocean’s Key Points: Beaufort Gyre is analyzed with the aim of understanding the mechanism driving the observed variability • Beaufort Gyre mooring on timescales of tens of days (i.e., subinertial). We employ a coherency/phase analysis on the temperature measurements of velocity and and horizontal velocity signals, which indicates that subinertial temperature variations arise from vertical temperature are analyzed for subinertial signal excursions of the water column that are driven by horizontal motions across the sloping seafloor. The • Observations are consistent vertical displacements of the water column (recorded by the temperature signal) show a bottom-intensified with topographic Rossby waves signature (i.e., decay toward the surface), while horizontal velocity anomalies are approximately barotropic propagating on sloping seafloor • Topographic Rossby waves play a role below the main halocline. We show that the different characteristics in vertical and horizontal velocities are in Beaufort Gyre stabilization consistent with topographic Rossby wave theory in the limit of weak vertical decay. In essence, a linearly decaying vertical velocity profile implies that the whole water column is stretched/squashed uniformly with Correspondence to: depth when water moves horizontally across the bottom slope. Thus, for the uniform stratification of the B.