DOCSLIB.ORG

Rossby Wave -- Coastal Kelvin Wave

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Rossby Wave -- Coastal Kelvin Wave 2382 JOURNAL OF PHYSICAL OCEANOGRAPHY VOLUME 29 Rossby Wave±Coastal Kelvin Wave Interaction in the Extratropics. Part I: Low-Frequency Adjustment in a Closed Basin ZHENGYU LIU,LIXIN WU, AND ERIC BAYLER Department of Atmospheric and Oceanic Sciences, University of WisconsinÐMadison, Madison, Wisconsin (Manuscript received 12 May 1998, in ®nal form 12 November 1998) ABSTRACT The interaction of open and coastal oceans in a midlatitude ocean basin is investigated in light of Rossby and coastal Kelvin waves. The basinwide pressure adjustment to an initial Rossby wave packet is studied both analytically and numerically, with the focus on the low-frequency modulation of the resulting coastal Kelvin wave. It is shown that the incoming mass is redistributed by coastal Kelvin waves as well as eastern boundary planetary waves, while the incoming energy is lost mostly to short Rossby waves at the western boundary. The amplitude of the Kelvin wave is determined by two mass redistribution processes: a fast process due to the coastal Kelvin wave along the ocean boundary and a slow process due to the eastern boundary planetary wave in the interior ocean. The amplitude of the Kelvin wave is smaller than that of the incident planetary wave because the initial mass of the Rossby wave is spread to the entire basin. In a midlatitude ocean basin, the slow eastern boundary planetary wave is the dominant mass sink. The resulting coastal Kelvin wave peaks when the peak of the incident planetary wave arrives at the western boundary. The theory is also extended to an extratropical±tropical basin to shed light on the modulation effect of extratropical oceanic variability on the equatorial thermocline. In contrast to a midlatitude basin, the fast mass redistribution becomes the dominant process, which is now accomplished mainly by equatorial Rossby and Kelvin waves, rather than the coastal Kelvin wave. The coastal Kelvin wave and the modulation of the equatorial thermocline peak close to the time when the wave trail of the incident Rossby wave arrives at the western boundary. Finally, the theory is also applied to the wave interaction around an extratropical island. 1. Introduction es (Pedlosky 1987). Coastal Kelvin waves will also be excited. However, the mechanism responsible for the In a midlatitude ocean basin, the two most important coastal Kelvin wave is not fully understood. This will low-frequency waves are the Rossby wave and coastal be the major question to be explored here. Kelvin wave. Most previous works have focused on the Rossby wave. Long Rossby waves (or planetary waves) The interaction of midlatitude Rossby and coastal are important for the adjustment in the interior ocean, Kelvin waves has at least three applications. First, it is while short Rossby waves are responsible for the in- an important process that contributes to the exchange tensive current variability along the western boundary of open and coastal ocean variability. Second, the coast- (e.g., Pedlosky 1965, 1987; Anderson and Gill 1975; al Kelvin wave generated by decadal planetary waves Cane and Sarachik 1977, 1979; McCreary and Kundu in the midlatitude may provide a mechanism for the 1988). However, relatively less attention has been paid modulation of the equatorial thermocline and therefore to the role of the coastal Kelvin wave and its interaction contributes to decadal climate variability in the sub- with Rossby waves in the low-frequency variability of tropical±tropical climate system (Lysne et al. 1997). the midlatitude ocean. In particular, there have been few Third, this interaction, as will be seen later, is critical studies on the interaction of Rossby waves and coastal for the low-frequency variability of island circulation. Kelvin waves on the western boundary. When a Rossby Previous works on the interaction of Rossby and wave incident is on the midlatitude western boundary, Kelvin waves can be divided into three groups. The ®rst it is known that short Rossby waves are generated to group includes numerous studies that investigated the balance the incoming cross-shore mass and energy ¯ux- interaction of equatorial Kelvin wave and equatorial Rossby waves (e.g., McCreary 1976; Cane and Sarachik 1977, 1979; Kawase 1987). It is found that wave re- ¯ection is determined mainly by the balance of zonal Corresponding author address: Z. Liu, Department of Atmospheric mass transport. The alongshore mass distribution is ac- and Oceanic Sciences, University of WisconsinÐMadison, 1225 W. Dayton St., Madison, WI 53706-1695. complished by short Rossby waves, which contributes E-mail: [email protected] little to the zonal mass transport and therefore plays q 1999 American Meteorological Society SEPTEMBER 1999 LIU ET AL. 2383 little role in determining the re¯ected Kelvin and long address the following questions: What is the magnitude Rossby waves. These studies have laid the foundation of the slowly evolving coastal Kelvin wave, and when to our understanding of seasonal- to interannual climate does it peak? What are the major factors that determine variability, such as the ENSO in the Paci®c Ocean (e.g., the strength and timing of the Kelvin wave amplitude? McCreary 1983; Cane and Zebiak 1985; Battisti 1989, Furthermore, in a basin that includes the equator, what 1991; Kessler 1991) and the Somali Current system in is the impact of the wave interaction in the midlatitude the Indian Ocean (e.g., McCreary and Kundu 1988). on the modulation of the equatorial thermocline? A sim- However, it will be seen later that interaction of the ple analytical theory is ®rst developed to determine the equatorial Rossby and Kelvin waves differs signi®cantly amplitude evolution of the coastal Kelvin wave. Exten- from that between a midlatitude Rossby wave and a sive numerical experiments are performed to substan- coastal Kelvin wave (see more discussions in section tiate the theory. The modulation of the Kelvin wave is 5). found to be determined by two nonlocal mass redistri- The second group focused on the extratropical ocean, bution processes: one fast and the other slow. The for- but only along the eastern boundary. The primary issue mer is due to the coastal Kelvin wave current, while the is the generation of planetary waves by coastal Kelvin latter is attributed to the eastern boundary planetary waves along the eastern boundary (e.g., En®eld and wave. The amplitude evolution of the coastal Kelvin Allen 1980; White and Saur 1983; Jacobs et al. 1994; wave depends critically on the mass redistribution pro- McCalpin 1995). At low frequencies, coastal Kelvin cess. Different from the re¯ection of equatorial Rossby waves change the eastern boundary pressure, which in and Kelvin waves, which is determined by the balance turn generates planetary waves radiating westward into of cross-shelf mass ¯ux along the equator, the coastal the interior ocean. These studies are important to un- Kelvin wave is generated to balance the alongshore mass derstand the impact of annual to decadal variability of ¯ux of the incident long Rossby wave in the midlatitude. coastal upwelling on the interior ocean. The paper is arranged as follows. A QG theory is The third group investigated the interplay of midlat- developed in section 2 to illustrate the major processes itude Rossby waves and coastal Kelvin waves, mostly that determine the interaction between planetary waves along the western boundary. Most of these works orig- and coastal Kelvin waves in a midlatitude basin. Sup- inated from the issue of mass conservation (or the con- porting numerical experiments are carried out in a shal- sistency condition) in a quasigeostrophic (QG) model low-water model in section 3. The theory is then ex- in a midlatitude basin (McWilliams 1977; Flierl 1977; tended to a combined extratropical±tropical basin in sec- Dorofeyev and Larichev 1992; Millif and McWilliams tion 4 to study the modulation of midlatitude planetary 1994, hereafter MM). All these works strongly sug- waves on the equatorial thermocline. A summary and gested that the coastal Kelvin wave plays a key role in a brief comparison with the interaction of equatorial mass conservation. Our work is a further extension of Rossby and Kelvin waves are given in section 5. Finally, these works. Godfrey (1975) and McCreary and Kundu a direct application of our theory to the wave interaction (1988) have discussed some initial re¯ection processes around an island is given in the appendix. and some local dynamics with the focus on low lati- tudes. Dorofeyev and Larichev limited their discussion to a half-plane midlatitude ocean, and therefore it does 2. The theory not directly apply to a closed basin. Kelvin wave prop- a. Model and solution agation around a basin has also been discussed in nu- merical models (Cane and Sarachik 1979; McCreary The modeling study of MM assures convincingly that 1983; MM). As will be seen later, the modulation of a the initial adjustment of Rossby and coastal Kelvin coastal Kelvin wave is a nonlocal process due to the waves in a midlatitude ocean basin can be simulated in rapid propagation of the coastal Kelvin wave. Conse- a QG model. Indeed, a low-frequency Kelvin wave can quently, the response differs dramatically for different be approximated as an alongshore current because of ocean basins. The modeling study of MM shows a re- its rapid along boundary propagation. This so-called markable resemblance between the shallow-water model coastal Kelvin wave current (CKC) is nearly geostrophic and the quasigeostrophic model, after the consistency and can therefore be represented in a QG model. Math- 1/2 condition is imposed in the latter. This assures that the ematically, the speed of the Kelvin wave co 5 (g9D) principle mechanisms for the interaction of Rossby and is independent of forcing frequency, where g9 is the coastal Kelvin waves are contained in a QG system.
Load more

Recommended publications
  • An Application of Kelvin Wave Expansion to Model Flow Pattern Using in Oil Spill Simulation M
    Brigham Young University BYU ScholarsArchive 6th International Congress on Environmental International Congress on Environmental Modelling and Software - Leipzig, Germany - July Modelling and Software 2012 Jul 1st, 12:00 AM An Application of Kelvin Wave Expansion to Model Flow Pattern Using in Oil Spill Simulation M. A. Badri Follow this and additional works at: https://scholarsarchive.byu.edu/iemssconference Badri, M. A., "An Application of Kelvin Wave Expansion to Model Flow Pattern Using in Oil Spill Simulation" (2012). International Congress on Environmental Modelling and Software. 323. https://scholarsarchive.byu.edu/iemssconference/2012/Stream-B/323 This Event is brought to you for free and open access by the Civil and Environmental Engineering at BYU ScholarsArchive. It has been accepted for inclusion in International Congress on Environmental Modelling and Software by an authorized administrator of BYU ScholarsArchive. For more information, please contact [email protected], [email protected]. International Environmental Modelling and Software Society (iEMSs) 2012 International Congress on Environmental Modelling and Software Managing Resources of a Limited Planet, Sixth Biennial Meeting, Leipzig, Germany R. Seppelt, A.A. Voinov, S. Lange, D. Bankamp (Eds.) http://www.iemss.org/society/index.php/iemss-2012-proceedings ١ ٢ ٣ ٤ An Application of Kelvin Wave Expansion ٥ to Model Flow Pattern Using in Oil Spill ٦ Simulation ٧ ٨ 1 M.A. Badri ٩ Subsea R&D center, P.O.Box 134, Isfahan University of Technology, Isfahan, Iran ١٠ [email protected] ١١ ١٢ ١٣ Abstract: In this paper, data of tidal constituents from co-tidal charts are invoked to ١٤ determine water surface level and velocity.
    [Show full text]
  • Kelvin/Rossby Wave Partition of Madden-Julian Oscillation Circulations
    climate Article Kelvin/Rossby Wave Partition of Madden-Julian Oscillation Circulations Patrick Haertel Department of Earth and Planetary Sciences, Yale University, New Haven, CT 06511, USA; [email protected] Abstract: The Madden Julian Oscillation (MJO) is a large-scale convective and circulation system that propagates slowly eastward over the equatorial Indian and Western Pacific Oceans. Multiple, conflicting theories describe its growth and propagation, most involving equatorial Kelvin and/or Rossby waves. This study partitions MJO circulations into Kelvin and Rossby wave components for three sets of data: (1) a modeled linear response to an MJO-like heating; (2) a composite MJO based on atmospheric sounding data; and (3) a composite MJO based on data from a Lagrangian atmospheric model. The first dataset has a simple dynamical interpretation, the second provides a realistic view of MJO circulations, and the third occurs in a laboratory supporting controlled experiments. In all three of the datasets, the propagation of Kelvin waves is similar, suggesting that the dynamics of Kelvin wave circulations in the MJO can be captured by a system of equations linearized about a basic state of rest. In contrast, the Rossby wave component of the observed MJO’s circulation differs substantially from that in our linear model, with Rossby gyres moving eastward along with the heating and migrating poleward relative to their linear counterparts. These results support the use of a system of equations linearized about a basic state of rest for the Kelvin wave component of MJO circulation, but they question its use for the Rossby wave component. Keywords: Madden Julian Oscillation; equatorial Rossby wave; equatorial Kelvin wave Citation: Haertel, P.
    [Show full text]
  • Baroclinic Instability, Lecture 19
    19. Baroclinic Instability In two-dimensional barotropic flow, there is an exact relationship between mass 2 streamfunction ψ and the conserved quantity, vorticity (η)given by η = ∇ ψ.The evolution of the conserved variable η in turn depends only on the spatial distribution of η andonthe flow, whichisd erivable fromψ and thus, by inverting the elliptic relation, from η itself. This strongly constrains the flow evolution and allows one to think about the flow by following η around and inverting its distribution to get the flow. In three-dimensional flow, the vorticity is a vector and is not in general con­ served. The appropriate conserved variable is the potential vorticity, but this is not in general invertible to find the flow, unless other constraints are provided. One such constraint is geostrophy, and a simple starting point is the set of quasi-geostrophic equations which yield the conserved and invertible quantity qp, the pseudo-potential vorticity. The same dynamical processes that yield stable and unstable Rossby waves in two-dimensional flow are responsible for waves and instability in three-dimensional baroclinic flow, though unlike the barotropic 2-D case, the three-dimensional dy­ namics depends on at least an approximate balance between the mass and flow fields. 97 Figure 19.1 a. The Eady model Perhaps the simplest example of an instability arising from the interaction of Rossby waves in a baroclinic flow is provided by the Eady Model, named after the British mathematician Eric Eady, who published his results in 1949. The equilibrium flow in Eady’s idealization is illustrated in Figure 19.1.
    [Show full text]
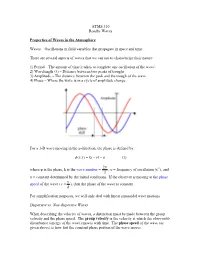
  • ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves
    ATMS 310 Rossby Waves Properties of Waves in the Atmosphere Waves – Oscillations in field variables that propagate in space and time. There are several aspects of waves that we can use to characterize their nature: 1) Period – The amount of time it takes to complete one oscillation of the wave\ 2) Wavelength (λ) – Distance between two peaks of troughs 3) Amplitude – The distance between the peak and the trough of the wave 4) Phase – Where the wave is in a cycle of amplitude change For a 1-D wave moving in the x-direction, the phase is defined by: φ ),( = −υtkxtx − α (1) 2π where φ is the phase, k is the wave number = , υ = frequency of oscillation (s-1), and λ α = constant determined by the initial conditions. If the observer is moving at the phase υ speed of the wave ( c ≡ ), then the phase of the wave is constant. k For simplification purposes, we will only deal with linear sinusoidal wave motions. Dispersive vs. Non-dispersive Waves When describing the velocity of waves, a distinction must be made between the group velocity and the phase speed. The group velocity is the velocity at which the observable disturbance (energy of the wave) moves with time. The phase speed of the wave (as given above) is how fast the constant phase portion of the wave moves. A dispersive wave is one in which the pattern of the wave changes with time. In dispersive waves, the group velocity is usually different than the phase speed. A non- dispersive wave is one in which the patterns of the wave do not change with time as the wave propagates (“rigid” wave).
    [Show full text]
  • TTL Upwelling Driven by Equatorial Waves
    TTL Upwelling driven by Equatorial Waves L09804 LIUWhat drives the annual cycle in TTL upwelling? ET AL.: START OF WATER VAPOR AND CO TAPE RECORDERS L09804 Liu et al. (2007) Ortland, D. and M. J. Alexander, The residual mean circula8on in the TTL driven by tropical waves, JAS, (in review), 2013. Figure 1. (a) Seasonal variation of 10°N–10°S mean EOS MLS water vapor after dividing by the mean value at each level. (b) Seasonal variation of 10°N–10°S EOS MLS CO after dividing by the mean value at each level. represented in two principal ways. The first is by the area of [8]ConcentrationsofwatervaporandCOnearthe clouds with low infrared brightness temperatures [Gettelman tropical tropopause are available from retrievals of EOS et al.,2002;Massie et al.,2002;Liu et al.,2007].Thesecond MLS measurements [Livesey et al.,2005,2006].Monthly is by the area of radar echoes reaching the tropopause mean water vapor and CO mixing ratios at 146 hPa and [Alcala and Dessler,2002;Liu and Zipser, 2005]. In this 100 hPa in the 10°N–10°Sand10° longitude boxes are study, we examine the areas of clouds that have TRMM calculated from one full year (2005) of version 1.5 MLS Visible and Infrared Scanner (VIRS) 10.8 mmbrightness retrievals. In this work, all MLS data are processed with temperatures colder than 210 K, and the area of 20 dBZ requirements described by Livesey et al. [2005]. Tropopause echoes at 14 km measured by the TRMM Precipitation temperature is averaged from the 2.5° resolution NCEP Radar (PR).
    [Show full text]
  • ATOC 5051: Introduction to Physical Oceanography HW #4: Given Oct
    ATOC 5051: Introduction to Physical Oceanography HW #4: Given Oct. 21; Due Oct 30 1. [15pts] Figure 1 shows the longitude - time plot of the Depth of 20°C isotherm Anomaly (D20A) along the Pacific equator from Jan 2004-Jan 2005. D20 represents the depth of the central thermocline in the equatorial Pacific, which deepens by as much as 30m in January 2004 and to a lesser degree, Jan 2005. Note that positive D20A represents thermocline ! deepening and negative D20A, thermocline shoaling. D20 anomaly (m) (a) From Figure 1, estimate the wave period and propagation speed, and calculate the wavelength. Provide discussions on how you obtain these estimates. (6pts) The period of the wave, which is the time it spans the two phase lines, is T=~80days. Take 1°~110km. The time it takes the wave to cross the basin, with Width=100°=100x110000m=11x106m, is ~50days. Therefore, cp=Width/(50*86400)=2.5(m/s). Based on the definition, wavelength 170E 90W L=T*cp=80*86400*2.5=17280(km). (b) From Figure 1, can you infer whether they are Figure 1. D20A along the equatorial symmetric or anti-symmetric waves, why? (3pts) Pacific from Jan 2004-Jan 2005. From Fig. 1, I infer that they’re symmetric waves Units are meters (m). The two solid because D20A, which mirrors sea level anomaly, lines represent the phase lines of obtains large amplitude on the equator. For anti- two waves, which also represent the symmetric waves, D20 and sea level are ~0 at the propagating fronts of deepened equator.
    [Show full text]
  • Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect Along Western Boundaries with Bottom Topography and Dissipation
    JANUARY 2020 W I S E E T A L . 217 Leaky Slope Waves and Sea Level: Unusual Consequences of the Beta Effect along Western Boundaries with Bottom Topography and Dissipation ANTHONY WISE National Oceanography Centre, and Department of Earth, Ocean and Ecological Sciences, University of Liverpool, Liverpool, United Kingdom CHRIS W. HUGHES Department of Earth, Ocean and Ecological Sciences, University of Liverpool, and National Oceanography Centre, Liverpool, United Kingdom JEFF A. POLTON AND JOHN M. HUTHNANCE National Oceanography Centre, Liverpool, United Kingdom (Manuscript received 5 April 2019, in final form 29 October 2019) ABSTRACT Coastal trapped waves (CTWs) carry the ocean’s response to changes in forcing along boundaries and are important mechanisms in the context of coastal sea level and the meridional overturning circulation. Motivated by the western boundary response to high-latitude and open-ocean variability, we use a linear, barotropic model to investigate how the latitude dependence of the Coriolis parameter (b effect), bottom topography, and bottom friction modify the evolution of western boundary CTWs and sea level. For annual and longer period waves, the boundary response is characterized by modified shelf waves and a new class of leaky slope waves that propagate alongshore, typically at an order slower than shelf waves, and radiate short Rossby waves into the interior. Energy is not only transmitted equatorward along the slope, but also eastward into the interior, leading to the dissipation of energy locally and offshore. The b effectandfrictionresultinshelfandslope waves that decay alongshore in the direction of the equator, decreasing the extent to which high-latitude variability affects lower latitudes and increasing the penetration of open-ocean variability onto the shelf—narrower conti- nental shelves and larger friction coefficients increase this penetration.
    [Show full text]
  • The Counter-Propagating Rossby-Wave Perspective on Baroclinic Instability
    Q. J. R. Meteorol. Soc. (2005), 131, pp. 1393–1424 doi: 10.1256/qj.04.22 The counter-propagating Rossby-wave perspective on baroclinic instability. Part III: Primitive-equation disturbances on the sphere 1∗ 2 1 3 CORE By J. METHVEN , E. HEIFETZ , B. J. HOSKINS and C. H. BISHOPMetadata, citation and similar papers at core.ac.uk 1 Provided by Central Archive at the University of Reading University of Reading, UK 2Tel-Aviv University, Israel 3Naval Research Laboratories/UCAR, Monterey, USA (Received 16 February 2004; revised 28 September 2004) SUMMARY Baroclinic instability of perturbations described by the linearized primitive equations, growing on steady zonal jets on the sphere, can be understood in terms of the interaction of pairs of counter-propagating Rossby waves (CRWs). The CRWs can be viewed as the basic components of the dynamical system where the Hamil- tonian is the pseudoenergy and each CRW has a zonal coordinate and pseudomomentum. The theory holds for adiabatic frictionless flow to the extent that truncated forms of pseudomomentum and pseudoenergy are globally conserved. These forms focus attention on Rossby wave activity. Normal mode (NM) dispersion relations for realistic jets are explained in terms of the two CRWs associated with each unstable NM pair. Although derived from the NMs, CRWs have the conceptual advantage that their structure is zonally untilted, and can be anticipated given only the basic state. Moreover, their zonal propagation, phase-locking and mutual interaction can all be understood by ‘PV-thinking’ applied at only two ‘home-bases’— potential vorticity (PV) anomalies at one home-base induce circulation anomalies, both locally and at the other home-base, which in turn can advect the PV gradient and modify PV anomalies there.
    [Show full text]
  • MAST602: Introduction to Physical Oceanography (Andreas Münchow) (Closed Book In-Class Rossby Wave Exercise, Oct.-21, 2008)
    MAST602: Introduction to Physical Oceanography (Andreas Münchow) (Closed book in-class Rossby Wave Exercise, Oct.-21, 2008) In a series of papers published in the 1930ies Carl-Gustaf Rossby introduced a strange new wave form whose existence has not been confirmed observationally until the late 1990ies. A debate is presently raging if and how these waves may impact ecosystems in the ocean, e.g., “Killworth et al., 2003: Physical and biological mechanisms for planetary waves observed in satellite-derived chlorophyll, J. Geophys. Res.” and “Dandonneau et al., 2003: Oceanic Rossby waves acting as a “Hay Rake” for ecosystem floating by- products, Science” as well as a flurry of comments generated by these papers. These peculiar waves originate from a linear balance between local acceleration, Coriolis acceleration, and pressure gradients as well as continuity of mass, that is, East-west momentum balance: ∂u/∂t – fv = -g ∂η/∂x North-south momentum balance: ∂v/∂t + fu = -g ∂η/∂y Continuity: ∂η/∂t + H (∂u/∂x+∂v/∂y) = 0 where the Coriolis parameter f = 2 Ω sin(latitude) is no longer a constant, but is approximated locally as f ≈ f0 + βy. The rotational rate of the earth is Ω=2π/day and at the -4 -1 -11 -1 -1 latitude of Lewes, DE (39N), f0~0.9×10 s and β~2×10 m s . A number of peculiar properties can be inferred from its dispersion relation: σ = − β κ / (κ2+l2+R-2) where σ is the wave frequency, κ is the wave number in the east-west direction, l is the wave number in the north-south direction, β is a constant (the so-called beta-parameter 1/2 that incorporates Coriolis effects that changes with latitude), and R=(g’H) /f0 is a constant (the so-called Rossby radius of deformation, the same as the lateral decay scale of the Kelvin wave, where g’~9.81×10-3m/s2 is the constant of “reduced” gravity, and H~1000 m is the depth of the pycnocline (density interface).
    [Show full text]
  • Downloaded 09/27/21 10:05 AM UTC 166 JOURNAL of PHYSICAL OCEANOGRAPHY VOLUME 43
    JANUARY 2013 C O N S T A N T I N 165 Some Three-Dimensional Nonlinear Equatorial Flows ADRIAN CONSTANTIN* King’s College London, London, United Kingdom (Manuscript received 28 March 2012, in final form 11 October 2012) ABSTRACT This study presents some explicit exact solutions for nonlinear geophysical ocean waves in the b-plane approximation near the equator. The solutions are provided in Lagrangian coordinates by describing the path of each particle. The unidirectional equatorially trapped waves are symmetric about the equator and prop- agate eastward above the thermocline and beneath the near-surface layer to which wind effects are confined. At each latitude the flow pattern represents a traveling wave. 1. Introduction The aim of the present paper is to provide an explicit nonlinear solution for geophysical waves propagating The complex dynamics of flows in the Pacific Ocean eastward in the layer above the thermocline and beneath near the equator presents certain specific features. The the near-surface layer in which wind effects are notice- equatorial region is characterized by a thin, permanent, able. The solution is presented in Lagrangian coordinates shallow layer of warm (and less dense) water overlying by describing the circular path of each particle. Within a deeper layer of cold water. The two layers are separated a narrow equatorial band the flow pattern describes an byasharpthermocline and a plausible assumption is that equatorially trapped wave that is symmetric about the there is no motion in the deep layer—see, for example, equator: at each fixed latitude we have a traveling wave Fedorov and Brown (2009).
    [Show full text]
  • Thompson/Ocean 420/Winter 2005 Tide Dynamics 1
    Thompson/Ocean 420/Winter 2005 Tide Dynamics 1 Tide Dynamics Dynamic Theory of Tides. In the equilibrium theory of tides, we assumed that the shape of the sea surface was always in equilibrium with the forcing, even though the forcing moves relative to the Earth as the Earth rotates underneath it. From this Earth-centric reference frame, in order for the sea surface to “keep up” with the forcing, the sea level bulges need to move laterally through the ocean. The signal propagates as a surface gravity wave (influenced by rotation) and the speed of that propagation is limited by the shallow water wave speed, C = gH , which at the equator is only about half the speed at which the forcing moves. In other t = 0 words, if the system were in moon equilibrium at a time t = 0, then by the time the Earth had rotated through an angle , the bulge would lag the equilibrium position by an angle /2. Laplace first rearranged the rotating shallow water equations into the system that underlies the tides, now known as the Laplace tidal equations. The horizontal forces are: acceleration + Coriolis force = pressure gradient force + tractive force. As we discussed, the tide producing forces are a tiny fraction of the total magnitude of gravity, and so the vertical balance (for the long wavelength appropriate to tidal forcing) remains hydrostatic. Therefore, the relevant force, the tractive force, is the projection of the tide producing force onto the local horizontal direction. The equations are the same as those that govern rotating surface gravity waves and Kelvin waves.
    [Show full text]
  • The Intraseasonal Equatorial Oceanic Kelvin Wave and the Central Pacific El Nino Phenomenon Kobi A
    The intraseasonal equatorial oceanic Kelvin wave and the central Pacific El Nino phenomenon Kobi A. Mosquera Vasquez To cite this version: Kobi A. Mosquera Vasquez. The intraseasonal equatorial oceanic Kelvin wave and the central Pacific El Nino phenomenon. Climatology. Université Paul Sabatier - Toulouse III, 2015. English. NNT : 2015TOU30324. tel-01417276 HAL Id: tel-01417276 https://tel.archives-ouvertes.fr/tel-01417276 Submitted on 15 Dec 2016 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. 1 2 This thesis is dedicated to my daughter, Micaela. 3 Acknowledgments To my advisors, Drs. Boris Dewitte and Serena Illig, for the full academic support and patience in the development of this thesis; without that I would have not reached this goal. To IRD, for the three-year fellowship to develop my thesis which also include three research stays in the Laboratoire d'Etudes en Géophysique et Océanographie Spatiales (LEGOS). To Drs. Pablo Lagos and Ronald Woodman, Drs. Yves Du Penhoat and Yves Morel for allowing me to develop my research at the Instituto Geofísico del Perú (IGP) and the Laboratoire d'Etudes Spatiales in Géophysique et Oceanographic (LEGOS), respectively.
    [Show full text]