DOCSLIB.ORG

Modeling and Simulation of a Free-Piston Engine with Electrical Generator Using HCCI Combustion

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Modeling and Simulation of a Free-Piston Engine with Electrical Generator Using HCCI Combustion Graduate Theses, Dissertations, and Problem Reports 2016 Modeling and Simulation of a Free-Piston Engine with Electrical Generator Using HCCI Combustion Mohammad Alrbai Follow this and additional works at: https://researchrepository.wvu.edu/etd Recommended Citation Alrbai, Mohammad, "Modeling and Simulation of a Free-Piston Engine with Electrical Generator Using HCCI Combustion" (2016). Graduate Theses, Dissertations, and Problem Reports. 5086. https://researchrepository.wvu.edu/etd/5086 This Dissertation is protected by copyright and/or related rights. It has been brought to you by the The Research Repository @ WVU with permission from the rights-holder(s). You are free to use this Dissertation in any way that is permitted by the copyright and related rights legislation that applies to your use. For other uses you must obtain permission from the rights-holder(s) directly, unless additional rights are indicated by a Creative Commons license in the record and/ or on the work itself. This Dissertation has been accepted for inclusion in WVU Graduate Theses, Dissertations, and Problem Reports collection by an authorized administrator of The Research Repository @ WVU. For more information, please contact [email protected]. Modeling and Simulation of a Free-Piston Engine with Electrical Generator Using HCCI Combustion ____________________________________________ Mohammad Alrbai Dissertation Submitted to the Benjamin M. Statler College of Engineering and Mineral Resources at West Virginia University in partial fulfillment of the requirements for the degree of Doctorate of Philosophy in Mechanical Engineering Nigel Clark, Ph.D., Chair Hailin Li, Ph.D. Cosmin Dumitrescu, Ph.D. Terence Musho, Ph.D. Fernando V. Lima, Ph.D. Department of Mechanical and Aerospace Engineering Morgantown, West Virginia 2016 Keywords: Free Piston Engine, Electrical Generator, Chemical kinetics, HCCI Combustion, Model Control, EGR, Equivalence Ratio. Copyright 2016 Mohammad Alrbai ABSTRACT Modeling and Simulation of a Free-Piston Engine with Electrical Generator using HCCI Combustion Mohammad Alrbai Free-piston engines have the potential to challenge the conventional crankshaft engines by their design simplicity and higher operational efficiency. Many studies have been performed to overcome the limitations of the free-piston devices especially the stability and control issues The investigations within the presented dissertation aim to satisfy many objectives by employing the approach of chemical kinetics to present the combustion process in the free-piston engine. This approach in addition to its advanced accuracy over the empirical methods, it has many other features like the ability to analyze the engine emissions. The effect of the heat release rate (HRR) on the engine performance is considered as the main objective. Understanding the relation between the HRR and the piston dynamics helps in enhancing the system efficiency and identifying the parameters that affect the overall performance. The dissertation covers some other objectives that belongs to the combustion phasing. Exhaust gas recirculation (EGR), equivalence ratio and the intake temperature represent the main combustion parameters, which have been discussed in this dissertation. To obtain the stability in system performance, the model requires a proper controller to simulate the operation and manage the different system parameters; for this purpose, different controlling techniques have been employed. In addition, the dissertation considers some other topics like engine emissions, fuels and fuels mechanisms. The model of the study describes the processes within a single cylinder, two stroke engine, which includes springs to support higher frequencies, reduce cyclic variations and sustain the engine compression ratio. An electrical generator presents the engine load; the generator supports different load profiles and play the key role in controlling the system. The 1st law of thermodynamics and Newton`s 2nd law are applied to couple the piston dynamics with the engine thermodynamics. The model governing equations represent a single zone perfectly stirred reactor (PSR) which contain a perfect mixing ideal gas mixture. The chemical kinetics approach is applied using Cantera/ MATLAB® toolbox, which presents the combustion process. In this research, a homogenous charge compression ignition (HCCI) at different operational conditions is used. HCCI engines have high efficiencies and low emissions and can work within a wide range of fuels. The results have been presented in a multi-cycle simulation and a parametric study forms. In the case of the multi-cycle simulation, a 100 cycles of the engine operation have been simulated. The overall work that is delivered to the electrical generator presents 47% of the total fuel energy. The model indicates an average frequency of 125 Hz along the operational cycles. In order to eliminate the cyclic variations and ensure a continuous operation, a proportional derivative (PD) controller has been employed. The controller adjusts the generator load in order to minimize the difference between the bottom dead center (BDC) locations along the operation cycles. The PD controller shows weakness in achieving the full steady state operation, for this purpose; a proportional integral (PI) controller has been implemented. The PI controller seeks to achieve a specific compression ratio. The results show that; the PI controller indicates unique behavior after 15 cycles of operation where the model ended to fluctuate between two compression ratios only. The complex relation between the thermodynamics and the dynamics of the engine is the greatest challenge in examining the effectiveness of the PI controller. In the parametric investigations, EGR examinations show that NOx emission is reduced to less than the half, as 30 % of EGR is used; this occurs due to the EGR thermal and dilution effects, which cause significant drop in the peak bulk temperature and CO emissions as well. Under the applied conditions, EGR has the ability to raise the work output ratio by increasing the engine compression ratio. The examination of the EGR temperature on the engine performance indicates that cooled EGR charges have the advantage over the hot EGR mixtures on enhancing the work output ratio. At the same time, EGR temperature affects the NOx formation by speeding its instantaneous reactions rate. The dissertation includes a study of the effect of the intake temperature and the equivalence ratio (φ) as well. The increasing in the intake temperature reduce the time needed for ignition, but leads to a reduction in the work output ratio at the same time. Such results can help in studying high knock resistance fuels where ignition delay is a matter. In the case of the equivalence ratio, lean mixtures show efficiencies that exceed 50% compared to those at the stoichiometric conditions. In the case of the ultra-lean (φ<0.5) combustion, the results show that the NOx emission is with the minimal levels as well as the CO and the unburned hydrocarbons (UHC) emissions. Sensitivity analysis to the chemical kinetic mechanism for the fuel combustion has been presented also in the dissertation. Many mechanisms for different fuels have been investigated, for example; a modified mechanism for Methane that includes 36 species and 222 reactions has been compared with the full GRI 3.0 mechanism (53 species and 325 reactions). The results of this comparison indicate that the modified mechanism has the potential to replace the full one in some cases like in demonstrating the engine operation, but not in the engine emissions analysis. I. Dedication I dedicate this work to my parents and to all of my family members. iv II. Acknowledgments First, I would like to thank Allah for his guidance and care during my whole life. I could not have met the challenges of this research without him. All of the appreciations and thanks go to my advisor Dr. Nigel Clark and my Co. Advisor Dr. Hailin Li. In addition, I want to thank all of the other committee members, Dr. Terence Musho, Dr. Cosmin Dumitrescu, and Dr. Fernando V. Lima. Their help and Advices were the motivators of my work. Special thanks goes to Dr. Hany Ammar for his continuous support along my study. At the same time, many thanks go to George Berry Chair for the financial support during this research. Finally, thanks to all of those friends, colleagues, instructors, and mentors who gave some of their time to make this work successful. v III. Table of Contents Dedication………………………………………………………………………………………………………………………………………………iv Acknowledgments…………………………………………………………………………………………………………………………………..v Table of Contents……………………………………………………………………………………………………………………………..…...vi List of Figures……………….…………………………………………………………………………………………………………….….……...ix List of Tables....................................................................................................................................….........xi List of Nomenclature…………………………………………………………………………………………………………………….….……xii Chapter 1. Introduction ................................................................................................................1 1.1 Linear engine ................................................................................................................................. 1 1.2 Homogeneous charge compression ignition engines ................................................................... 1 1.3 Review of literature .....................................................................................................................
Load more

Recommended publications
  • 2013 KIVA Development
    2013 DOE Merit Review 2013 KIVA Development David Carrington Los Alamos National Laboratory May 13, 2013 Project ID # ACE014 This presentation does not contain any proprietary, confidential, or otherwise restricted information LA-UR-13-21976 2013 DOE Overview Merit Review Timeline Barriers • Improve understanding of the fundamentals of • 10/01/09 fuel injection, fuel-air mixing, thermodynamic combustion losses, and in-cylinder combustion/ • 09/01/14 emission formation processes over a range of combustion temperature for regimes of interest • 65% complete by adequate capability to accurately simulate these processes • Engine efficiency improvement and engine- Budget out emissions reduction • Minimization of engine technology development • Total project funding to date: – User friendly (industry friendly) software, robust, accurate, more predictive, & quick meshing – 2000K – 640K in FY 12 Partners – Contractor (Universities) share ~40% • University of New Mexico- Dr. Juan Heinrich • University of Purdue, Calumet - Dr. Xiuling • Funding to date for FY13 - 210K Wang • Funding anticipated FY13 – 763K • University of Nevada, Las Vegas - Dr. Darrell W. Pepper 2 2013 DOE FY 09 to FY 14 KIVA-Development Merit Review Objectives • Robust, Accurate Algorithms in a Modular Object-Oriented code– • Relevance to accurately predicting engine processes to enable better understanding of, flow, thermodynamics, sprays, in easy to use software for moderate computer platforms – More accurate modeling requires new algorithms and their correct implementation. – Developing more robust and accurate algorithms • To understand better combustion processes in internal engines – Providing a better mainstay tool • improving engine efficiencies and • help in reducing undesirable combustion products. – Newer and mathematically rigorous algorithms will allow KIVA to meet the future and current needs for combustion modeling and engine design.
    [Show full text]
  • Catalytically Generating and Utilizing Hydrogen to Reduce Nox Emissions in Automobile Applications
    Catalytically Generating and Utilizing Hydrogen to Reduce NOx Emissions in Automobile Applications Thesis by Nawaf Mohammed Alghamdi In Partial Fulfillment of the Requirements For the Degree of Master of Science King Abdullah University of Science and Technology Thuwal, Kingdom of Saudi Arabia November, 2018 2 EXAMINATION COMMITTEE PAGE The thesis of Nawaf Mohammed Alghamdi is approved by the examination committee. Committee Chairperson: Professor Mani Sarathy Committee Members: Professor Jorge Gascon and Professor Aamir Farooq 3 © November, 2018 Nawaf Mohammed Alghamdi All Rights Reserved 4 ABSTRACT Catalytically Generating and Utilizing Hydrogen to Reduce NOx Emissions in Automobile Applications Nawaf Mohammed Alghamdi Heterogeneous catalysis is a powerful chemical technology because it can enhance the conversion of reactants, promote selectivity to a desired product, and lower the reaction temperature requirements. The breaking and forming of chemical bonds in heterogeneous catalysis is facilitated on a solid surface where adsorbed gas-phase species react and form products. This study is concerned with utilizing heterogeneous catalysis in the automobile industry via the generation and utilization of hydrogen to reduce NOx emissions. In spark ignition engines, the three-way-catalyst technology is ineffective at the more efficient, lean-burn conditions. In compression-ignition engines, an ammonia-based technology is implemented but has associated high cost and ammonia slip challenges. This motivates providing an alternative technology, such as hydrogen selective catalytic reduction (H2- SCR). In this study, four catalysts were investigated for the lean-burn selective catalytic reduction of NO using hydrogen. The catalysts were platinum (Pt) and palladium (Pd) noble metals supported on cerium oxide (CeO2) and magnesium oxide (MgO).
    [Show full text]
  • Combustion Research Facility – Industry Interactions and Impact
    Combustion Research Facility – Industry Interactions and Impact Bob Hwang Director, Transportation Energy Center Sandia National Laboratories, Livermore, CA Sandia Sites Albuquerque, New Mexico Livermore, California Kauai, Hawaii Pantex Plant, Amarillo, Texas Waste Isolation Pilot Plant, Tonopah, Carlsbad, New Mexico Nevada 2 CRF - Understanding Combustion Processes A Clearly Defined Partnership Mission from the Beginning • Born out of gasoline crises of 1970’s – created in 1980 • Built to tap into strengths of existing NNSA laboratory – Premier optical diagnostics – High Performance Computing – Flagship experimental facilities • Teaming at DOE – Office of Science unwavering “Do great science” mandate • “Basic Energy Sciences (BES) supports fundamental research to understand, predict, and ultimately control matter and energy at the electronic, atomic, and molecular levels in order to provide the foundations for new energy technologies and to support DOE missions in energy, environment, and national security.” – Vehicle Technologies partnership: “make an impact” • “The U.S. Department of Energy's Vehicle Technologies Office supports research, development (R&D), and deployment of efficient and sustainable highway transportation technologies to improve vehicles’ fuel economy and minimize petroleum use.” • Strong industrial and academic ties from day #1 Combustion Research Facility A DOE Collaborative Research Facility dedicated to energy science and technology for the twenty-first century • Leadership in combustion research since 1980 • 8200-m2
    [Show full text]
  • Comodia 2012
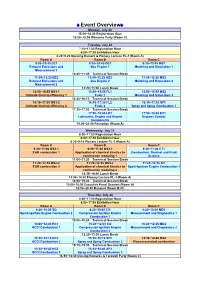
    ♦Event Overview♦ Monday, July 23 15:00~18:00 Registration Hour 16:00~18:00 Welcome Party (Room C) Tuesday, July 24 7:10~17:00 Registration Hour 8:00~17:30 Exhibition Hour 8:20~9:20 Opening Remark & Plenary Lecture PL-1 (Room A) Room A Room B Room C 9:30~10:45 EE1 9:30~10:45 GE1 9:30~10:45 MS1 Exhaust Emissions and Gas Engine 1 Modeling and Simulation 1 Measurement 1 10:45~11:05 Technical Session Break 11:05~12:20 EE2 11:05~12:20 GE2 11:05~12:20 MS2 Exhaust Emissions and Gas Engine 2 Modeling and Simulation 2 Measurement 2 12:20~13:50 Lunch Break 13:50~15:55 OS1-1 13:50~15:55 FL1 13:50~15:55 MS3 Ultimate thermal efficiency 1 Fuels 1 Modeling and Simulation 3 15:55~16:15 Technical Session Break 16:15~17:30 OS1-2 16:15~17:30 FL2 16:15~17:30 SP1 Ultimate thermal efficiency 2 Fuels 2 Spray and Spray Combustion 1 17:30~17:50 Technical Session Break 17:50~18:40 LE1 17:50~18:40 EC1 Lubricants, Engine and Engine Engines Control Components 19:00~21:00 Reception (Room A) Wednesday, July 25 8:00~17:00 Registration Hour 8:00~17:30 Exhibition Hour 8:20~9:10 Plenary Lecture PL-2 (Room A) Room A Room B Room C 9:20~11:00 OS2-1 9:20~11:00 OS3-1 9:20~11:00 CT1 EGR combustion 1 Application of chemical kinetics to Combustion, Thermal and Fluid combustion modeling 1 Science 11:00~11:20 Technical Session Break 11:20~12:35 OS2-2 11:20~12:35 OS3-2 11:20~12:35 SI1 EGR combustion 2 Application of chemical kinetics to Spark-Ignition Engine Combustion 1 combustion modeling 2 12:35~14:00 Lunch Break 14:00~14:50 Plenary Lecture PL-3 (Room A) 14:50~15:00 Technical Session
    [Show full text]
  • VALVE CONTROLS INFINITE POSSIBILITIES ROGER STONE, CAMCON AUTOMOTIVE TECHNICAL DIRECTOR Where All the Pieces Fall Into Place
    The pan-European magazine of SAE International May/June 2013 VALVE CONTROLS INFINITE POSSIBILITIES ROGER STONE, CAMCON AUTOMOTIVE TECHNICAL DIRECTOR Where All the Pieces Fall Into Place Let’s face it; driveline design can be a real brainteaser. Reduced emissions. Improved fuel economy. Enhanced vehicle performance. Getting all the pieces to fit is challenging—especially when you can’t see the whole picture. That’s why you need one more piece to solve the driveline puzzle. Introducing DrivelineNEWS.com—a single, all-encompassing website exclusively dedicated to driveline topics for both on- and off-road vehicles. Log on for the latest news, market intelligence, technical innovations and hardware animations to help you find solutions and move your business forward. It takes ingenuity and persistence to succeed in today’s driveline market. Test your skills at DrivelineNEWS.com/Puzzle. Solve the puzzle to enter to win a Kindle Fire. © 2013 The Lubrizol Corporation. All rights reserved. 121569 Contents 12 12 Cover Story 5 Comment Valve controls Imagine a valve control system that is infinitely 6 variable irrespective of engine speed and load. News Impossible? Not according to Camcon Automotive’s • Exclusive: technical director Roger Stone, as Ian Adcock Engine knock discovers predicted 16 Biomimicry • Volvo diesel breakthrough Mother Nature knows best What can the automotive industry learn from nature • Driveline software when it comes to weight saving? Ryan Borroff has 20 been finding out • Four-way cat for petrol engines 20 Fuel injection systems Building up the pressure 11 Tony Lewin reports on the growing trend towards even The Columnist higher line pressures in injection systems.
    [Show full text]
  • The Kinetics of Nitrogen Oxides Formation in the Flame Gas
    A Service of Leibniz-Informationszentrum econstor Wirtschaft Leibniz Information Centre Make Your Publications Visible. zbw for Economics Zajemska, Monika; Poskart, Anna; Musiał, Dorota Article The kinetics of nitrogen oxides formation in the flame gas Economic and Environmental Studies (E&ES) Provided in Cooperation with: Opole University Suggested Citation: Zajemska, Monika; Poskart, Anna; Musiał, Dorota (2015) : The kinetics of nitrogen oxides formation in the flame gas, Economic and Environmental Studies (E&ES), ISSN 2081-8319, Opole University, Faculty of Economics, Opole, Vol. 15, Iss. 4, pp. 445-460 This Version is available at: http://hdl.handle.net/10419/178898 Standard-Nutzungsbedingungen: Terms of use: Die Dokumente auf EconStor dürfen zu eigenen wissenschaftlichen Documents in EconStor may be saved and copied for your Zwecken und zum Privatgebrauch gespeichert und kopiert werden. personal and scholarly purposes. Sie dürfen die Dokumente nicht für öffentliche oder kommerzielle You are not to copy documents for public or commercial Zwecke vervielfältigen, öffentlich ausstellen, öffentlich zugänglich purposes, to exhibit the documents publicly, to make them machen, vertreiben oder anderweitig nutzen. publicly available on the internet, or to distribute or otherwise use the documents in public. Sofern die Verfasser die Dokumente unter Open-Content-Lizenzen (insbesondere CC-Lizenzen) zur Verfügung gestellt haben sollten, If the documents have been made available under an Open gelten abweichend von diesen Nutzungsbedingungen die in der dort Content Licence (especially Creative Commons Licences), you genannten Lizenz gewährten Nutzungsrechte. may exercise further usage rights as specified in the indicated licence. www.econstor.eu www.ees.uni.opole.pl ISSN paper version 1642-2597 ISSN electronic version 2081-8319 Economic and Environmental Studies Vol.
    [Show full text]
  • 12Th Diesel Engine-Efficiency and Emissions Research (DEER
    7/28/06 3 p.m. 12th Diesel Engine-Efficiency and Emissions Research Conference Detroit Marriott at the Renaissance Center August 20-24, 2006 ---------- PLENARY SESSIONS ---------- Monday, August 21, 2006 8:30 a.m. - Noon A View from the Bridge Panel Discussion Andrew Karsner, Assistant Secretary for Energy Efficiency and Renewable Energy at the U.S. Department of Energy Elizabeth Lowery, Vice-President for Environment and Energy at General Motors Gerhard Schmidt, Vice-President for Research and Advanced Engineering at Ford Motor Company Margo Ogé, Director of the Office of Transportation and Air Quality at the U.S. Environmental Protection Agency (EPA) John K. Amdall, Director of Engine Research and Development at Caterpillar Tom Cackette, Chief Deputy Executive Officer at the California Air Resources Board Michael Walsh, environmental consultant Tuesday, August 22, 2006 8:30 a.m. - Noon Accelerating Light-Duty Diesel Sales in the U.S. Market Panel Discussion Charles Freese, General Motors Simon Godwin, DaimlerChrysler Kevin McMahon, Martec Group Karl Simon, EPA Wolfgang Mattes, BMW Yasuyuki Sando, Senior Manager, Advanced Engine Research Division at Honda Klaus-Peter Schindler, Volkswagen 1 Wednesday, August 23, 2006 8:30 a.m. - Noon New Feedstocks and Replacement Fuels Panel Discussion Loren Beard, DaimlerChrysler (invited) Norman Brinkman, General Motors Nigel Clark, West Virginia University Herb Dobbs, TACOM Craig Fairbridge, National Centre for Upgrading Technology Robert McCormick, National Renewable Energy Laboratory James Simnick, BP ________ TECHNICAL SESSIONS _______ Monday, August 21, 2006 1:30 – 4:10 p.m. Technical Session 1 – Advanced Combustion Technologies, Part 1 Title Speaker Affiliation Heavy-Duty HCCI Development Kevin Duffy Caterpillar Activities at Caterpillar Low-Temperature Combustion for Dennis Assanis University of High-Efficiency, Ultra-Low Emission Michigan Engines Evaluation of High-Efficiency Clean Robert M.
    [Show full text]
  • Oak Ridge National Laboratory Capabilities
    FEMP Team Capabilities at ORNL in Buildings and Fleets Managed by UT-Battelle for the Department of Energy ORNL FEMP Team — Primary Work-for-Others Technical Assistance Capabilities Customers • Geothermal (ground-source) heat pumps • DOE • Combined heat and power (CHP, • US Navy distributed energy, cogeneration) • Marine Corps • Benchmarking and strategic energy • US Army management • Air Force • Industrial energy efficiency • Coast Guard • Energy assessments • Environmental Protection Agency • Alternative financing • Housing and Urban • Measurement & Development verification • Fish and Wildlife Service • Commissioning, O&M • Tennessee Valley Authority • Federal design/construction practices • State of California • General technical/design assistance • New York State ERDA – LEED, Energy Star, life-cycle cost, modeling, etc. 2 Managed by UT-Battelle for the Department of Energy 1 Geothermal Heat Pumps — Retrofits or New Construction ORNL’s independent design review and simulation modeling for residential GHP • Feasibility studies systems for Marine Corps Air Station Beaufort, South Carolina (“Fightertown”) • Life-cycle-cost studies contributed to the success of the project. • Review of technical and price proposals • Review of system design • Interpretation of thermal properties tests • Review of bore field sizing • Baseline and energy savings estimates/ calculations • Review of pricing • Development of building simulation models • Development of measurement and verification plans 3 Managed by UT-Battelle for the Department of Energy Presentation_name
    [Show full text]
  • SAE 2011 World Congress & Exhibition
    SAE 2011 World Congress & Exhibition Technical Session Schedule As of 04/18/2011 07:40 pm Tuesday, April 12 New Transmission Technologies That Could Change the Face of Powertrain Performance Session Code: ANN200 Room FEV Powertrain Innovation Forum Session Time: 10:00 a.m. New transmission concepts and developments are occurring in parallel with new innovations in engine technology, allowing OEMs to produce powertrain systems that meet both government regulatory mandates while still giving the consumer the drivability they have come to expect. Not only have the number of speeds increased, new types of transmissions and control strategies are coming to market. These include DCT, electrically assisted AMT, electrically assisted hybrid automatics, etc. Transmission experts on the panel will discuss new development trends, control and calibration strategies as well as provide a glimpse into the future for these new design trends. Moderators - Mircea Gradu, Director Transmission & Driveline Engrg, Chrysler Group LLC Panelists - Thomas Brown, General Mgr, Drivetrain Engrg, Aisin Tech. Center of America; Kiran Govindswamy, Chief Engineer, NVH, CAE & Driveline Systems, FEV, Inc.; Steven G. Thomas, Mgr, Transmission/Driveline, Res & Adv Engrg, Ford Motor Co.; Hamid Vahabzadeh, General Director, Global Adv Trans Engrg, GM Powertrain; Andy Yu, Vice President Engineering, BorgWarner Inc.; Tuesday, April 12 Charging Forward Toward 2017: The Powertrains That Will Get Us There Session Code: ANN201 Room FEV Powertrain Innovation Forum Session Time: 1:00 p.m. While much of the regulatory attention may be shifting to CAFE, ozone and CO2 limits proposed by both CARB and EPA for 2017 to 2025, the 2016 regulations still must be met.
    [Show full text]
  • Alternative Ad.Qxd
    P001_ADEU_MAY11.qxp:Layout 1 23/5/11 18:28 Page 1 The pan-European magazine of SAE International May/June 2011 Variable compression ratio reborn CFD combustion analysis Lighting the way Exhaust materials SAE Review P002_ADEU_MAY11 19/5/11 10:38 Page 1 WITHOUT DUAL CLUTCH TRANSMISSION TECHNOLOGY, YOU’RE JUST GETTING LEFT BEHIND. Maybe it’s the fact that in the time you read this, a Dual Clutch Transmission could switch gears 40,000 times. Perhaps it’s the fact that DCTs appeal to more buyers by combining impressive fuel-economy, the smooth ride of an automatic and the speed of a manual. It could be the fact that leading clutch suppliers estimate they’ll quadruple DCT sales by 2014. Or maybe it’s the fact that by 2015, 10% of all passenger cars will have them. DCTFACTS.COM gives you endless reasons to believe that DCTs are the future generation DCTFACTS.COM of transmissions. And the more you know about them, the further ahead you’ll get. P003_ADEU_MAY11.qxp:Layout 1 23/5/11 18:18 Page 3 Contents 16 16 Spotlight on Bernie Rosenthal 5 Comment Ian Adcock talks with the Reaction Design CEO After the bad.... about the company’s ground-breaking computional comes the good fluid dynamics package for combustion analysis. 6 News 22 Cover feature Laser spark sees the Consumption: The Mother of Invention light • Two eyes are It’s a challenge that has engaged the minds of many better than one • down the years: changing the compression ratio in an Avago launches first engine on the fly.
    [Show full text]
  • ASME® 2018 ICEF Internal Combustion Engine Fall Technical Conference
    ASME® 2018 ICEF Internal Combustion Engine Fall Technical Conference CONFERENCE November 4 – 7, 2018 EXHIBITION November 5 – 6, 2018 Hilton San Diego Resort & Spa Program San Diego, CA e American Society of Mechanical Engineers® ASME® Technical Sessions MONDAY, NOVEMBER 5 TRACK 3 ADVANCED COMBUSTION TRACK 2 FUELS Track Chair: Sundar Rajan Krishnan, University of Alabama, Tuscaloosa, AL, United States Track Chair: Gregory Bogin, Colorado School of Mines, Golden, CO, United States Track Co-Chair: Cosmin Dumitrescu, West Virginia University, Morgantown, WV, United States Track Co-Chair: Hailin Li, West Virginia University, Morgantown, WV, United States 3-1 FUNDAMENTALS/SI/THERMODYNAMICS SAN DIEGO, CA, HILTON RESORT & SPA, SORRENTO 2-1 SPARK IGNITION, FUEL SPRAYS AND IGNITION KINETICS 10:00AM - 12:00PM SAN DIEGO, CA, HILTON RESORT & SPA, LAS PALMAS 10:00AM - 12:00PM Session Chair: Hui Xu, Cummins Inc., Columbus, IN, United States Session Chair: Douglas Longman, Argonne Natl Lab., Argonne, IL, United Session Co-Chair: Joshua Bittle, University of Alabama, Tuscaloosa, AL, States United States, Tiegang Fang, NC State University, Raleigh, NC, United States, Isaac Ekoto, 7011 East avenue, Livermore, CA, United States Session Co-Chair: Scott Wayne, West Virginia University, Morgantown, WV, United States EFFECT OF DIRECT FUEL INJECTION STRATEGY ON COMBUSTION, PERFORMANCE AND EMISSIONS OF A PORT FUEL INJECTED EXPERIMENTAL INVESTIGATIONS OF HYDROGEN-NATURAL GAS COMPRESSED NATURAL GAS ENGINE USING SIMULATION TOOLS ENGINES FOR MARITIME APPLICATIONS
    [Show full text]
  • Diesel Engines
    p r o g r a m m E September 14th˜17th, 2010 ValencIa (SpaIn) THIESEL · 2010 conference on: Thermo-and fluid dynamic processes in Diesel Engines ORGANISED BY: CMT – MoTores TérMiCos. Universidad Politécnica de valencia, Spain Bienvenida Welcome Una vez más, un año más, La Universidad Politécnica Once more, this year again, the Universidad Politécnica de de Valencia acoge la conferencia THIESEL sobre Procesos Valencia is hosting the THIESEL Conference on Thermo-and Termofluidodinámicos en motores Diesel. Esta es la 6ª edición, Fluid Dynamic Processes in Diesel Engines. This is its 6th con lo que se puede asegurar que el proyecto está consolidado edition, which confirms that it is by now a well consolidated y aparece como cita obligada en el calendario internacional project. It has also become a must in the international de encuentros científicos sobre motores Diesel. calendar of scientific meetings about Diesel engines. Cada edición ha mostrado una particularidad, y en este caso, Each of the editions has had its own particularity. This one will be ha sido en primer lugar los acontecimientos económicos y marked on the one hand by the economical and financial events financieros que han afectado de forma especial al sector de that have especially affected the automotive sector, and on the automoción. Y por otra parte la aparición de un contexto que parece other hand, by the new trend that favours the implementation favorecer la implantación de la tracción eléctrica en los turismos. of the electrical powertrain in light-duty vehicles. Con todo ello, los que estamos en este sector, seguimos All things considered, we who work in this sector, still pensando que los motores térmicos, y en particular el motor believe that thermal engines, and in particular Diesel engines, Diesel aún tienen mucho camino por recorrer, y buena prueba have yet plenty of kilometres to travel.
    [Show full text]