DOCSLIB.ORG

18-Animation.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
18-Animation.Pdf Advertisement Computer Animation Adam Finkelstein Princeton University COS 426, Spring 2003 Computer Animation 3-D and 2-D animation • What is animation? o Make objects change over time according to scripted actions • What is simulation? Pixar o Predict how objects change over time according to physical laws Homer 3-D Homer 2-D University of Illinois Outline Principles of Traditional Animation • Principles of animation • Squash and stretch • Keyframe animation • Slow In and out • Anticipation • Articulated figures • Exaggeration • Kinematics • Follow through and overlapping action • Timing •Dynamics • Staging • Straight ahead action and pose-to-pose action •Arcs • Secondary action • Appeal Angel Plate 1 Disney 1 Principles of Traditional Animation Principles of Traditional Animation • Squash and stretch • Slow In and Out Lasseter `87 Watt Figure 13.5 Principles of Traditional Animation Principles of Traditional Animation • Anticipation (and squash & stretch) • Squash and stretch • Slow In and out • Anticipation • Exaggeration • Follow through and overlapping action • Timing • Staging • Straight ahead action and pose-to-pose action •Arcs • Secondary action • Appeal Lasseter `87 Disney Computer Animation Keyframe Animation Animation pipeline • Define character poses at specific time steps o 3D modeling called “keyframes” o Articulation o Motion specification o Motion simulation o Shading o Lighting o Rendering o Postprocessing » Compositing Pixar Lasseter `87 2 Keyframe Animation Keyframe Animation • Interpolate variables describing keyframes to • Inbetweening: determine poses for character “in-between” o Linear interpolation - usually not enough continuity Linear interpolation Lasseter `87 H&B Figure 16.16 Keyframe Animation Keyframe Animation • Inbetweening: • Inbetweening: o Spline interpolation - maybe good enough o Cubic spline interpolation - maybe good enough » May not follow physical laws H&B Figure 16.11 Lasseter `87 Keyframe Animation Keyframe Animation • Inbetweening: • Inbetweening: o Cubic spline interpolation - maybe good enough o Inverse kinematics or dynamics » May not follow physical laws Lasseter `87 Rose et al. `96 3 Outline Articulated Figures • Principles of animation • Character poses described by set of rigid bodies connected by “joints” • Keyframe animation • Articulated figures Base • Kinematics • Dynamics Arm Hand Scene Graph Angel Plate 1 Angel Figures 8.8 & 8.9 Articulated Figures Articulated Figures • Well-suited for humanoid characters Joints provide handles for moving articulated figure Root Chest LHip RHip Neck LCollar LCollar LKnee RKnee Head LShld LShld LAnkle RAnkle LElbow LElbow LWrist LWrist Rose et al. `96 Mike Marr, COS 426, Princeton University, 1995 Articulated Figures Example: Walk Cycle • Inbetweening • Articulated figure: o Compute joint angles between keyframes Good arm Bad arm Watt & Watt Watt & Watt 4 Example: Walk Cycle Example: Walk Cycle • Hip joint orientation: • Knee joint orientation: Watt & Watt Watt & Watt Example: Walk Cycle Example: Run Cycle • Ankle joint orientation: Watt & Watt Mike Marr, COS 426, Princeton University, 1995 Example: Ice Skating Outline • Principles of animation • Keyframe animation • Articulated figures • Kinematics • Dynamics (Mao Chen, Zaijin Guan, Zhiyan Liu, Xiaohu Qie, CS426, Fall98, Princeton University) Angel Plate 1 5 Kinematics and Dynamics Example: 2-Link Structure • Kinematics • Two links connected by rotational joints o Considers only motion o Determined by positions, velocities, accelerations Θ •Dynamics 2 “End-Effector” o Considers underlying forces 2 o Compute motion from initial conditions and physics 1 X = (x,y) Θ1 (0,0) Forward Kinematics Forward Kinematics • Animator specifies joint angles: Θ1 and Θ2 • Joint motions can be specified by spline curves • Computer finds positions of end-effector: X Θ2 2 Θ2 2 X = (x,y) 1 X = (x,y) Θ1 1 (0,0) Θ Θ1 1 (0,0) Θ2 t X = (l1 cosΘ1 + l2 cos(Θ1 + Θ2 ),l1 sin Θ1 + l2 sin(Θ1 + Θ2 )) Forward Kinematics Example: 2-Link Structure • Joint motions can be specified by initial conditions • What if animator knows position of “end-effector” and velocities Θ2 Θ2 “End-Effector” 2 2 X = (x,y) X = (x,y) 1 1 Θ1 o o Θ1 (0,0) Θ1(0) = 60 Θ2 (0) = 250 (0,0) dΘ dΘ 1 =1.2 2 = −0.1 dt dt 6 Inverse Kinematics Inverse Kinematics • Animator specifies end-effector positions: X • End-effector postions can be specified by splines • Computer finds joint angles: Θ1 and Θ2: Θ2 2 Θ2 2 X = (x,y) X = (x,y) 1 Θ 1 x2 + x2 − l 2 − l 2 1 −1 1 2 (0,0) Θ2 = cos Θ1 x 2l1l2 (0,0) − (l sin(Θ )x + (l + l cos(Θ ))y 2 2 1 2 2 y Θ1 = t (l2 sin(Θ2 ))y + (l1 + l2 cos(Θ2 ))x Inverse Kinematics Inverse Kinematics • Problem for more complex structures • Solution for more complex structures: o System of equations is usually under-defined o Find best solution (e.g., minimize energy in motion) o Multiple solutions o Non-linear optimization X = (x,y) X = (x,y) Θ2 Θ2 3 3 2 2 Θ3 Θ3 1 1 Θ1 Θ1 Three unknowns: Θ , Θ , Θ (0,0) 1 2 3 Two equations: x, y (0,0) Summary of Kinematics Overview • Forward kinematics • Kinematics o Specify conditions (joint angles) o Considers only motion o Compute positions of end-effectors o Determined by positions, velocities, accelerations • Inverse kinematics •Dynamics o “Goal-directed” motion o Considers underlying forces o Specify goal positions of end effectors o Compute motion from initial conditions and physics o Compute conditions required to achieve goals InverseInverse kinematicskinematics providesprovides easiereasier specificationspecification forfor manymany animationanimation tasks,tasks, but it is computationally more difficult 7 Dynamics Spacetime Constraints • Simulation of physics insures realism of motion • Animator specifies constraints: o What the character’s physical structure is » e.g., articulated figure o What the character has to do » e.g., jump from here to there within time t o What other physical structures are present » e.g., floor to push off and land o How the motion should be performed » e.g., minimize energy Lasseter `87 Spacetime Constraints Spacetime Constraints • Computer finds the “best” physical motion • Discretize time steps: satisfying constraints x − x x' = i i−1 • Example: particle with jet propulsion i h o x(t) is position of particle at time t xi+1 − 2xi + xi−1 x''i = o f(t) is force of jet propulsion at time t h2 o Particle’s equation of motion is: mx''− f − mg = 0 xi+1 − 2xi + xi−1 m x''i = − fi − mg = 0 h2 o Suppose we want to move from a to b within t0 to t1 with minimum jet fuel: t 1 2 2 Minimizef (t) dt subject to x(t0)=a and x(t1)=b Minimizeh∑ fi subject to x0=a and x1=b ∫ i t0 Witkin & Kass `88 Witkin & Kass `88 Spacetime Constraints Spacetime Constraints • Solve with • Advantages: iterative o Free animator from having to specify details of optimization physically realistic motion with spline curves methods o Easy to vary motions due to new parameters and/or new constraints • Challenges: o Specifying constraints and objective functions o Avoiding local minima during optimization Witkin & Kass `88 8 Spacetime Constraints Spacetime Constraints • Adapting motion: • Adapting motion: Original Jump Hurdle Heavier Base Witkin & Kass `88 Witkin & Kass `88 Spacetime Constraints Spacetime Constraints • Adapting motion: • Editing motion: Ski Jump Witkin & Kass `88 Li et al. `99 Spacetime Constraints Dynamics • Morphing motion: • Other physical simulations: o Rigid bodies o Soft bodies o Cloth o Liquids o Gases o etc. Cloth (Baraff & Witkin `98) Hot Gases Gleicher `98 (Foster & Metaxas `97) 9 Summary • Principles of animation • Keyframe animation • Articulated figures • Kinematics o Forward kinematics o Inverse kinematics •Dynamics o Space-time constraints o Also other physical simulations 10.
Load more

Recommended publications
  • Motion Enriching Using Humanoide Captured Motions
    MASTER THESIS: MOTION ENRICHING USING HUMANOIDE CAPTURED MOTIONS STUDENT: SINAN MUTLU ADVISOR : A NTONIO SUSÌN SÀNCHEZ SEPTEMBER, 8TH 2010 COURSE: MASTER IN COMPUTING LSI DEPERTMANT POLYTECNIC UNIVERSITY OF CATALUNYA 1 Abstract Animated humanoid characters are a delight to watch. Nowadays they are extensively used in simulators. In military applications animated characters are used for training soldiers, in medical they are used for studying to detect the problems in the joints of a patient, moreover they can be used for instructing people for an event(such as weather forecasts or giving a lecture in virtual environment). In addition to these environments computer games and 3D animation movies are taking the benefit of animated characters to be more realistic. For all of these mediums motion capture data has a great impact because of its speed and robustness and the ability to capture various motions. Motion capture method can be reused to blend various motion styles. Furthermore we can generate more motions from a single motion data by processing each joint data individually if a motion is cyclic. If the motion is cyclic it is highly probable that each joint is defined by combinations of different signals. On the other hand, irrespective of method selected, creating animation by hand is a time consuming and costly process for people who are working in the art side. For these reasons we can use the databases which are open to everyone such as Computer Graphics Laboratory of Carnegie Mellon University. Creating a new motion from scratch by hand by using some spatial tools (such as 3DS Max, Maya, Natural Motion Endorphin or Blender) or by reusing motion captured data has some difficulties.
    [Show full text]
  • The University of Chicago Looking at Cartoons
    THE UNIVERSITY OF CHICAGO LOOKING AT CARTOONS: THE ART, LABOR, AND TECHNOLOGY OF AMERICAN CEL ANIMATION A DISSERTATION SUBMITTED TO THE FACULTY OF THE DIVISION OF THE HUMANITIES IN CANDIDACY FOR THE DEGREE OF DOCTOR OF PHILOSOPHY DEPARTMENT OF CINEMA AND MEDIA STUDIES BY HANNAH MAITLAND FRANK CHICAGO, ILLINOIS AUGUST 2016 FOR MY FAMILY IN MEMORY OF MY FATHER Apparently he had examined them patiently picture by picture and imagined that they would be screened in the same way, failing at that time to grasp the principle of the cinematograph. —Flann O’Brien CONTENTS LIST OF FIGURES...............................................................................................................................v ABSTRACT.......................................................................................................................................vii ACKNOWLEDGMENTS....................................................................................................................viii INTRODUCTION LOOKING AT LABOR......................................................................................1 CHAPTER 1 ANIMATION AND MONTAGE; or, Photographic Records of Documents...................................................22 CHAPTER 2 A VIEW OF THE WORLD Toward a Photographic Theory of Cel Animation ...................................72 CHAPTER 3 PARS PRO TOTO Character Animation and the Work of the Anonymous Artist................121 CHAPTER 4 THE MULTIPLICATION OF TRACES Xerographic Reproduction and One Hundred and One Dalmatians.......174
    [Show full text]
  • Randomized Path Planning for Redundant Manipulators Without Inverse Kinematics
    Randomized Path Planning for Redundant Manipulators without Inverse Kinematics Mike Vande Weghe Dave Ferguson, Siddhartha S. Srinivasa Institute for Complex Engineered Systems Intel Research Pittsburgh Carnegie Mellon University 4720 Forbes Avenue Pittsburgh, PA 15213 Pittsburgh, PA 15213 [email protected] {dave.ferguson, siddhartha.srinivasa}@intel.com Abstract— We present a sampling-based path planning al- gorithm capable of efficiently generating solutions for high- dimensional manipulation problems involving challenging inverse kinematics and complex obstacles. Our algorithm extends the Rapidly-exploring Random Tree (RRT) algorithm to cope with goals that are specified in a subspace of the manipulator configuration space through which the search tree is being grown. Underspecified goals occur naturally in arm planning, where the final end effector position is crucial but the configuration of the rest of the arm is not. To achieve this, the algorithm bootstraps an optimal local controller based on the transpose of the Jacobian to a global RRT search. The resulting approach, known as Jacobian Transpose-directed Rapidly Exploring Random Trees (JT-RRTs), is able to combine the configuration space exploration of RRTs with a workspace goal bias to produce direct paths through complex environments extremely efficiently, without the need for any inverse kinematics. We compare our algorithm to a recently- developed competing approach and provide results from both simulation and a 7 degree-of-freedom robotic arm. I. INTRODUCTION Path planning for robotic systems operating in real envi- ronments is hard. Not only must such systems deal with the standard planning challenges of potentially high-dimensional and complex search spaces, but they must also cope with im- perfect information regarding their surroundings and perhaps Fig.
    [Show full text]
  • A Closed-Form Solution for the Inverse Kinematics of the 2N-DOF Hyper-Redundant Manipulator Based on General Spherical Joint
    applied sciences Article A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint Ya’nan Lou , Pengkun Quan, Haoyu Lin, Dongbo Wei and Shichun Di * School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China; [email protected] (Y.L.); [email protected] (P.Q.); [email protected] (H.L.); [email protected] (D.W.) * Correspondence: [email protected]; Tel.: +86-1390-4605-946 Abstract: This paper presents a closed-form inverse kinematics solution for the 2n-degree of freedom (DOF) hyper-redundant serial manipulator with n identical universal joints (UJs). The proposed algorithm is based on a novel concept named as general spherical joint (GSJ). In this work, these universal joints are modeled as general spherical joints through introducing a virtual revolution between two adjacent universal joints. This virtual revolution acts as the third revolute DOF of the general spherical joint. Remarkably, the proposed general spherical joint can also realize the decoupling of position and orientation just as the spherical wrist. Further, based on this, the universal joint angles can be solved if all of the positions of the general spherical joints are known. The position of a general spherical joint can be determined by using three distances between this unknown general spherical joint and another three known ones. Finally, a closed-form solution for the whole manipulator is solved by applying the inverse kinematics of single general spherical joint section using these positions. Simulations are developed to verify the validity of the proposed closed-form inverse kinematics model.
    [Show full text]
  • Authoring Motion Cycles
    Authoring Motion Cycles Loïc Ciccone Martin Guay ETH Zurich Disney Research Zurich Maurizio Nitti Robert W. Sumner Disney Research Zurich ETH Zurich, Disney Research Zurich Figure 1: Left: To specify a motion cycle, the user acts out several loops of the motion using a variety of capture devices. Middle: A looping motion cycle is automatically extracted from the noisy performance. Right: A custom motion representation tool, called MoCurves, allows controlling and coordinating spatial and temporal transformations from a single viewport. ABSTRACT CCS CONCEPTS Motion cycles play an important role in animation production • Computing methodologies → Animation; Graphics systems and game development. However, creating motion cycles relies and interfaces; on general-purpose animation packages with complex interfaces that require expert training. Our work explores the specic chal- KEYWORDS lenges of motion cycle authoring and provides a system simple Motion cycles, Animation interface, Performance, Motion curves enough for novice animators while maintaining the exibility of control demanded by experts. Due to their cyclic nature, we show ACM Reference format: that performance animation provides a natural interface for mo- Loïc Ciccone, Martin Guay, Maurizio Nitti, and Robert W. Sumner. 2017. tion cycle specication. Our system allows the user to act several Authoring Motion Cycles. In Proceedings of ACM SIGGRAPH / Eurographics loops of motion using a variety of capture devices and automat- Symposium on Computer Animation, Los Angeles, California USA, July 2017 (SCA’17), 9 pages. ically extracts a looping cycle from this potentially noisy input. DOI: 10.475/123_4 Motion cycles for dierent character components can be authored in a layered fashion, or our method supports cycle extraction from higher-dimensional data for capture devices that deliver many de- 1 INTRODUCTION grees of freedom.
    [Show full text]
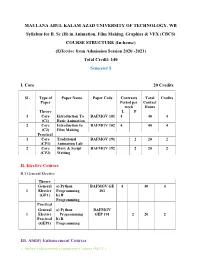
  • MAULANA ABUL KALAM AZAD UNIVERSITY of TECHNOLOGY, WB Syllabus for B. Sc (H) in Animation, Film Making, Graphics & VFX (CBCS)
    MAULANA ABUL KALAM AZAD UNIVERSITY OF TECHNOLOGY, WB Syllabus for B. Sc (H) in Animation, Film Making, Graphics & VFX (CBCS) COURSE STRUCTURE (In-house) (Effective from Admission Session 2020 -2021) Total Credit: 140 Semester I I. Core 20 Credits SL Type of Paper Name Paper Code Contracts Total Credits Paper Period per Contact week Hours Theory L P 1 Core Introduction To BAFMGV 101 4 40 4 (C1) Basic Animation 2 Core Introduction to BAFMGV 102 4 40 4 (C2) Film Making Practical 1 Core Traditional BAFMGV 191 2 20 2 (CP1) Animation Lab 2 Core Story & Script BAFMGV 192 2 20 2 (CP2) Writing II. Elective Courses B.1 General Elective Theory General a) Python BAFMGV GE 4 40 4 1 Elective Programming 101 (GE1) b) R Programming Practical General a) Python BAFMGV 1 Elective Programming GEP 191 2 20 2 Practical b) R (GEP1) Programming III. Ability Enhancement Courses 1. Ability Enhancement Compulsory Courses (AECC) Theory Ability Communicative BAFMGV AECC 1 Enhance English I 101 2 20 2 ment Compuls ory Courses (AECC1) Semester II I. Core 20 Credits SL Type of Paper Name Paper Code Contracts Total Credits Paper Period per Contact week Hours L P Theory Introduction to BAFMGV 201 1 Core (C3) Graphic Design 4 40 4 & Visual Art Introduction to BAFMGV 202 2 Core (C4) 2D Animation 4 40 4 Practical Digital Design, 1 Core Info graphics & BAFMGV 291 2 20 2 (CP3) Branding (Adobe Photoshop, illustrator, Corel Draw) 2 Core 2D animation lab BAFMGV 292 2 20 2 (CP4) (Flash) II. Elective Courses B.1 General Elective Theory General a) Web Design BAFMGV 1 Elective b)Computer GE201 4 40 4 (GE2) Networks Practical General a) Webpage BAFMGV 1 Elective Design GEP291 2 20 2 Practical (GEP2) b)Networking Lab III.
    [Show full text]
  • Multiple Dynamic Pivots Rig for 3D Biped Character Designed Along Human-Computer Interaction Principles
    Multiple Dynamic Pivots Rig for 3D Biped Character Designed along Human-Computer Interaction Principles by Mihaela D. Petriu A thesis submitted to the Faculty of Graduate and Postdoctoral Affairs in partial fulfillment of the requirements for the degree of Master of Computer Science in Human-Computer Interaction Carleton University Ottawa, Ontario © 2020, Mihaela D. Petriu Abstract This thesis is addressing the design, implementation and usability testing of a modular extensible animator-centric authoring tool-independent 3D Multiple Dynamic Pivots (MDP) biped character rig. An objective of the thesis is to show that the design of the character rig must be independent of its platform, cater to the needs of the animation workflow based on HCI principles (particularly that of Direct Manipulation) and be modular and extensible in order to build and grow as needed within the production pipeline. In the thesis, the proposed rig design is implemented in Maya, the most widely used and taught commercial 3D animation authoring tool. Another thesis objective is to perform usability testing of the MDP rig with animation students and professionals, in order to gauge the new design’s intuitiveness for those relatively new to the trade and those already steeped in its decades of accumulated technical idiosyncrasies. ii Acknowledgements My deepest gratitude goes to my supervisor Dr. Chris Joslin for his constant guidance and support. I would also like to thank my family for their continuous help and encouragement. Finally, I thank my friend Sandra E. Hobbs for her constructive chaos that shed light on my design's weaknesses. iii Table of Contents Abstract .............................................................................................................................
    [Show full text]
  • Video Puppetry: a Performative Interface for Cutout Animation
    Video Puppetry: A Performative Interface for Cutout Animation Connelly Barnes1 David E. Jacobs2 Jason Sanders2 Dan B Goldman3 Szymon Rusinkiewicz1 Adam Finkelstein1 Maneesh Agrawala2 1Princeton University 2University of California, Berkeley 3Adobe Systems Figure 1: A puppeteer (left) manipulates cutout paper puppets tracked in real time (above) to control an animation (below). Abstract 1 Introduction Creating animated content is difficult. While traditional hand- We present a video-based interface that allows users of all skill drawn or stop-motion animation allows broad expressive freedom, levels to quickly create cutout-style animations by performing the creating such animation requires expertise in composition and tim- character motions. The puppeteer first creates a cast of physical ing, as the animator must laboriously craft a sequence of frames puppets using paper, markers and scissors. He then physically to convey motion. Computer-based animation tools such as Flash, moves these puppets to tell a story. Using an inexpensive overhead Toon Boom and Maya provide sophisticated interfaces that allow camera our system tracks the motions of the puppets and renders precise and flexible control over the motion. Yet, the cost of pro- them on a new background while removing the puppeteer’s hands. viding such control is a complicated interface that is difficult to Our system runs in real-time (at 30 fps) so that the puppeteer and learn. Thus, traditional animation and computer-based animation the audience can immediately see the animation that is created. Our tools are accessible only to experts. system also supports a variety of constraints and effects including Puppetry, in contrast, is a form of dynamic storytelling that per- articulated characters, multi-track animation, scene changes, cam- 1 formers of all ages and skill levels can readily engage in.
    [Show full text]
  • Inverse Kinematics (IK) Solution of a Robotic Manipulator Using PYTHON
    Journal of Mechatronics and Robotics Original Research Paper Inverse Kinematics (IK) Solution of a Robotic Manipulator using PYTHON 1R. Venkata Neeraj Kumar and 2R. Sreenivasulu 1Department of Electrical Engineering, Indian Institute of Technology, Gandhinagar, Gujarat, India 2R.V.R.&J.C. College of Engineering (Autonomous), Chowdavaram, Guntur Andhra Pradesh, India Article history Abstract: Present global engineering professionals feels that, robotics is a Received: 20-07-2019 somewhat young field with extremely ruthless target, the crucial one being Revised: 06-08-2019 the making of machinery/equipment that can perform and feel like human Accepted: 22-08-2019 beings. Robot kinematics deals with the study of motion of linkages which includes displacement, velocities and accelerations of a robot manipulator Corresponding Author: analytically. Deriving the proper kinematic models for an open chain Dr. R. Sreenivasulu R.V.R.&J.C. College of mechanism of a robot is essential for analyzing the performance of industrial Engineering (Autonomous), robotic manipulators. In this study, first scrutinize a popular class of two and Chowdavaram, Guntur Andhra three degrees of freedom open chain mechanism whose inverse kinematics Pradesh, India admits a closed-form analytic solution. A simple coding was developed in Email: [email protected] python in an easy way. In this connection a two link planer manipulator was considered to get inverse kinematic solution developed in python environment. For this task, we present a solution for obtaining the joint variables of linkages to reach the position in a work space with the corresponding input values such as link lengths and position of end effector. Keywords: Robotic Manipulator, Inverse Kinematics, Joint Variables, PYTHON Introduction (1989) were used MACSYMA, REDUCE, SMP and SEGM methods, these methods requires typical Robot kinematics deals with the study of motion of mathematical concepts to achieve forward and inverse linkages which includes displacement, velocities and solutions.
    [Show full text]
  • Animation of a High-Definition 2D Fighting Game Character
    Tuula Rantala ANIMATION OF A HIGH-DEFINITION 2D FIGHTING GAME CHARACTER Thesis Kajaani University of Applied Sciences School of Business Business Information Technology Spring 2013 OPINNÄYTETYÖ TIIVISTELMÄ Koulutusala Koulutusohjelma Luonnontieteiden ala Tietojenkäsittely Tekijä(t) Tuula Rantala Työn nimi Teräväpiirtoisen 2d-taistelupelihahmon animointi Vaihtoehtoisetvaihtoehtiset ammattiopinnot Ohjaaja(t) Peligrafiikka Nick Sweetman Toimeksiantaja - Aika Sivumäärä ja liitteet Kevät 2013 56 Tämä opinnäytetyö pyrkii erittelemään hyvän pelihahmoanimaation periaatteita ja tarkastelee eri lähestymistapoja 2d-animaation luomiseen. Perinteisen animaation periaatteet, kuten ajoitus ja liikkeen välistys, pätevät pelianimaa- tiossa samalla tavalla kuin elokuva-animaatiossakin. Pelien tekniset rajoitukset ja interaktiivisuus asettavat kuiten- kin lisähaasteita animaatioiden toteuttamiseen tavalla, joka sekä tukee pelimekaniikkaa että on visuaalisesti kiin- nostava. Vetoava hahmoanimaatio on erityisen tärkeää taistelupeligenressä. Varhaiset taistelupelit 1990–luvun alusta käyt- tivät matalaresoluutioista bittikarttagrafiikkaa ja niissä oli alhainen määrä animaatiokehyksiä, mutta nykyään pelien standardit grafiikan ja animaation suhteen ovat korkealla. Viime vuosina monet pelinkehittäjät ovat siirtyneet käyttämään 2d-grafiikan sijasta 3d-grafiikkaa, koska 3d-animaation tuottaminen on monella tavalla joustavampaa. Perinteiselle 2d-grafiikalle on kuitenkin edelleen kysyntää, sillä käsin piirretyn animaation ainutlaatuista ulkoasua ei voi täysin korvata
    [Show full text]
  • Inverse Kinematics Problems with Exact Hessian Matrices
    Inverse Kinematics Problems with Exact Hessian Matrices Kenny Erleben Sheldon Andrews University of Copenhagen École de technologie supérieure [email protected] [email protected] ABSTRACT Popular techniques for solving IK problems typically discount Inverse kinematics (IK) is a central component of systems for mo- the use of exact Hessians, and prefer to rely on approximations of tion capture, character animation, motion planning, and robotics second-order derivatives. However, robotics work has shown that control. The eld of computer graphics has developed fast station- exact Hessians in 2D Lie algebra-based dynamical computations ary point solvers methods, such as the Jacobian transpose method outperforms approximate methods [Lee et al. 2005]. Encouraged by and cyclic coordinate descent. Much work with Newton methods these results, we examine the viability of exact Hessians for inverse focus on avoiding directly computing the Hessian, and instead ap- kinematics of 3D characters. To our knowledge, no previous work in proximations are sought, such as in the BFGS class of solvers. This computer graphics has addressed the signicance of using a closed paper presents a numerical method for computing the exact Hes- form solution for the exact Hessian, which is surprising since IK is sian of an IK system with spherical joints. It is applicable to human pertinent for many computer animation applications and there is a skeletons in computer animation applications and some, but not large body of work on the topic. all, robots. Our results show that using exact Hessians can give This paper presents the closed form solution in a simple and easy performance advantages and higher accuracy compared to standard to evaluate geometric form using two world space cross-products.
    [Show full text]
  • The Art of Animation
    UNIVERSITY OF CALIFORNIA College of Engineering Department of Electrical Engineering and Computer Sciences Computer Science Division CS 294-7 The Art Of Animation Professor Brian A. Barsky and Laurence Arcadias Fall 2002 Overview Class time and place The class is on Mondays, from 3 pm to 6 pm, in 380 Soda Hall. The first class is August 26 and the last class is December 2. There will be no class on Sept. 2 (Labor Day) nor on Nov.11 (Veterans Day). Computer lab The computer lab is located in 111 Cory. It is open from 7:30 am to 6:30 pm and is accessible by cardkey outside those hours. This multimedia instructional lab comprises: six Apple PowerMac G4 computers (each with 1.5 GB RAM, SuperDrive, 867 MHz CPU, NVIDIA GeForce2 MX graphics card, 80 GB hard drive, and a 250-MB ZIP drive, running MacOSX 10.1) eight Windows 2000 computers (each with Pentium III 931 MHz CPU and 256 MB RAM) Instructors Prof. Brian A. Barsky Office: 785 Soda Hall Phone: (510) 642-9838 E-mail: [email protected] Office hours: Monday 1 pm to 3 pm Laurence Arcadias Office: 329 Soda Hall Phone: (510) 642-9827; 643-4207 E-mail: E-mail: [email protected] Office hours: Monday 1 pm to 3 pm Course Summary This hands-on animation course is intended for students with a computer science background who would like to improve their sense of observation, timing, and motion through the real art of animation to create strong believable animation pieces. A good understanding of motion is an important foundation for using computers and technology to their full potential for the creation of animation.
    [Show full text]