DOCSLIB.ORG

Inverse Kinematics and Geometric Constraints for Articulated Fig

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Inverse Kinematics and Geometric Constraints for Articulated Fig INVERSE KINEMATICS AND GEOMETRIC CONSTRAINTS FOR ARTICULATED FIGURE MANIPULATION by Chris Welman BSc Simon Fraser University a thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in the Scho ol of Computing Science c Chris Welman SIMON FRASER UNIVERSITY Septemb er All rights reserved This work may not b e repro duced in whole or in part by photo copy or other means without the p ermission of the author APPROVAL Name Chris Welman Degree Master of Science Title of thesis Inverse Kinematics and Geometric Constraints for Articulated Fig ure Manipulation Examining Committee Dr L Hafer Chair Dr TW Calvert Senior Sup ervisor Dr J Dill Dr D Forsey External Examiner Date Approved ii Abstract Computer animation of articulated gures can b e tedious largely due to the amount of data which must b e sp ecied at each frame Animation techniques range from simple interp olation b etween keyframed gure p oses to higherlevel algorithmic mo dels of sp ecic movement patterns The former provides the animator with complete control over the movement whereas the latter may provide only limited control via some highlevel parameters incorp orated into the mo del Inverse kinematic techniques adopted from the rob otics literature have the p otential to relieve the animator of detailed sp ecication of every motion parameter within a gure while retaining complete control over the movement if desired This work investigates the use of inverse kinematics and simple geometric constraints as to ols for the animator Previous applications of inverse kinematic algorithms to computer animation are reviewed A pair of alternative algorithms suitable for a direct manipulationinterface are presented and qualitatively compared Application of these algorithms to enforce simple geometric constraints on a gure during interactive manipulation is discussed An implementation of one of these algo rithms within an existing gure animation editor is describ ed whichprovides constrained inverse kinematic gure manipulation for the creation of keyframes Contents Intro duction Organization Approaches to Figure Animation Bo dy Mo dels Scop e Skeleton Mo delling Kinematic Metho ds Forward Kinematics Inverse Kinematics Dynamic Metho ds Forward Dynamics Inverse Dynamics Control Issues Summary Inverse Kinematics The Inverse Kinematic Problem Resolved Motion Rate Control Redundancy Singularities OptimizationBased Metho ds Evaluation Applications to Computer Graphics Ecient Algorithms for Direct Manipulation A Simplied Dynamic Mo del The Jacobian Transp ose Metho d i CONTENTS ii Implementation Details Computing the Jacobian Scaling Considerations Integration Joint Limits A Complementary Heuristic Approach The CyclicCo ordinate Descent Metho d Overview Comparison Incorp orating Constraints Constraint Satisfaction Maintaining Constraints The Constraint Condition Computing the Constraint Jacobian Matrix Computing the ConstraintForce Solving for Lagrange Multipliers Feedback Overview Implementation Issues Skeletons as Ob jects Handles on Skeletons Constraints on Handles The Global Picture Summary A CCDbased Penalty Metho d An Interactive Editor A System Overview Skeletons The Sequence The Editor Direct Manipulation Constraints Conclusion Summary Results CONTENTS iii Comments ab out Constraints Directions Bibliography List of Figures a ob jects dened in lo cal co ordinate systems b Lo cal rotations applied cd Lo cal translations applied Three congurations of a D redundant manipulator A manipulator in a singular conguration Interactive control lo op mo del for Jacobian transp ose metho d A case not handled well with the Jacobian transp ose metho d Pulling inwards on the tip of the manipulator on the left will not pro duce an exp ected conguration like the one shown on the right Example CCD iteration step for rotation jointi A force applied to a p oint constrained to lie within a plane A constraining force normal to the plane is added to the applied force to obtain a legal force tangential to the plane Iteration steps for maintaining constraints A generic function blo ck Example network A branching chain with two endeector constraints Sample skeleton description Sequence editor screen Plan view of goal determination in a an orthographic view and b a p ersp ective view A gure b eing p ositioned by rst tilting then twisting the p elvis a First keyframe p ose b Interp olated p ose c Second keyframe p ose iv Chapter Intro duction Computer graphics has advanced to a p oint where generating images of striking realism and com plexity has b ecome almost commonplace However making ob jects moveconvincingly within these pictures remains dicult particularly as ob ject mo dels grow increasingly complex The sp ecication and control of motion for computer animation has emerged as one of the principal areas of research within the computer graphics community One area in particular which continues to receiveattention is that of gure animation The goal of work in this area is to provide a means of generating lifelike p ossibly humanlike articulated gures and to design and control their actions within simulated environments Animated human gures could for example b e placed in simulated environments for ergonomic evaluation or simply to provide some aesthetic qualities to a presentation In the arts and entertainment area the concept of computergenerated characters roaming through articial worlds seems universally app ealing Although gure animation raises technical challenges in b oth mo delling and rendering the fun damental problem of designing and controlling movement for these gures remains a particularly dicult one Part of the problem lies in deciding from whichlevel of detail to approach the task At one end of the scale the movements of individual parts of the b o dy must b e known for each instant in time At the other end of the scale co ordinating movements and handling interaction between gures and with the environmentmay require algorithms based on b ehavioural rules and knowledge bases Many of the most impressive examples of gure animation bycomputerhavebeen the result of algorithms implementing highlevel b ehavioural and motor control mo dels However these algorithms are often limited to generating sp ecic usually rep etitive movement patterns such as walking and running For the animator who wishes to create new movements there is little al ternative to painstakingly constructing the movementby hand Given the complex structure of a typical articulated gure this can involve an inordinate amountofwork CHAPTER INTRODUCTION The motivation b ehind this work is a desire to improve the animation capabilities of an existing interactive articulated gure animation package which is currently used to create movements for b oth dance and animation It is shown how inverse kinematic techniques for controlling rob otic manipulators can b e adopted to relieve the animator of some of the more tedious asp ects of creating new movements by hand After reviewing the inverse kinematic problem and solutions that have previously b een applied to gure animation a pair of alternative solution algorithms are presented and qualitatively compared These algorithms are simple yet eective and can supp ort b oth direct manipulation of articulated gures as well as the imp osition of simple geometric constraints up on a gure Implementations of these algorithms are presented and are applied to develop a basic set of interactive to ols for gure manipulation and animation Organization Chapter reviews computer animation techniques in general and discusses their applicabilityin the context of gure animation In Chapter the inverse kinematic problem is stated and com mon approaches to solving the problem are reviewed In Chapter a pair of fast reliable inverse kinematic algorithms are describ ed suitable for interactive manipulation tasks and diering from previous algorithms adopted for computer graphics In Chapter pro cedures for satisfying simple geometric constraints using these algorithms are considered Chapter intro duces an interactive gure animation editor and discusses implementation of the algorithms as p ositioning aids Chapter Approaches to Figure Animation Placing this work in context requires some understanding of computer animation techniques in general and of how they may b e applied to gure animation in particular This chapter provides an overview of the advantages and disadvantages of basic motion control techniques for gure animation The emphasis here is on metho ds to create and control the movements of articulated gures rather than simply replaying digitized movement It is fair to say that
Load more

Recommended publications
  • Randomized Path Planning for Redundant Manipulators Without Inverse Kinematics
    Randomized Path Planning for Redundant Manipulators without Inverse Kinematics Mike Vande Weghe Dave Ferguson, Siddhartha S. Srinivasa Institute for Complex Engineered Systems Intel Research Pittsburgh Carnegie Mellon University 4720 Forbes Avenue Pittsburgh, PA 15213 Pittsburgh, PA 15213 [email protected] {dave.ferguson, siddhartha.srinivasa}@intel.com Abstract— We present a sampling-based path planning al- gorithm capable of efficiently generating solutions for high- dimensional manipulation problems involving challenging inverse kinematics and complex obstacles. Our algorithm extends the Rapidly-exploring Random Tree (RRT) algorithm to cope with goals that are specified in a subspace of the manipulator configuration space through which the search tree is being grown. Underspecified goals occur naturally in arm planning, where the final end effector position is crucial but the configuration of the rest of the arm is not. To achieve this, the algorithm bootstraps an optimal local controller based on the transpose of the Jacobian to a global RRT search. The resulting approach, known as Jacobian Transpose-directed Rapidly Exploring Random Trees (JT-RRTs), is able to combine the configuration space exploration of RRTs with a workspace goal bias to produce direct paths through complex environments extremely efficiently, without the need for any inverse kinematics. We compare our algorithm to a recently- developed competing approach and provide results from both simulation and a 7 degree-of-freedom robotic arm. I. INTRODUCTION Path planning for robotic systems operating in real envi- ronments is hard. Not only must such systems deal with the standard planning challenges of potentially high-dimensional and complex search spaces, but they must also cope with im- perfect information regarding their surroundings and perhaps Fig.
    [Show full text]
  • A Closed-Form Solution for the Inverse Kinematics of the 2N-DOF Hyper-Redundant Manipulator Based on General Spherical Joint
    applied sciences Article A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint Ya’nan Lou , Pengkun Quan, Haoyu Lin, Dongbo Wei and Shichun Di * School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China; [email protected] (Y.L.); [email protected] (P.Q.); [email protected] (H.L.); [email protected] (D.W.) * Correspondence: [email protected]; Tel.: +86-1390-4605-946 Abstract: This paper presents a closed-form inverse kinematics solution for the 2n-degree of freedom (DOF) hyper-redundant serial manipulator with n identical universal joints (UJs). The proposed algorithm is based on a novel concept named as general spherical joint (GSJ). In this work, these universal joints are modeled as general spherical joints through introducing a virtual revolution between two adjacent universal joints. This virtual revolution acts as the third revolute DOF of the general spherical joint. Remarkably, the proposed general spherical joint can also realize the decoupling of position and orientation just as the spherical wrist. Further, based on this, the universal joint angles can be solved if all of the positions of the general spherical joints are known. The position of a general spherical joint can be determined by using three distances between this unknown general spherical joint and another three known ones. Finally, a closed-form solution for the whole manipulator is solved by applying the inverse kinematics of single general spherical joint section using these positions. Simulations are developed to verify the validity of the proposed closed-form inverse kinematics model.
    [Show full text]
  • Inverse Kinematics (IK) Solution of a Robotic Manipulator Using PYTHON
    Journal of Mechatronics and Robotics Original Research Paper Inverse Kinematics (IK) Solution of a Robotic Manipulator using PYTHON 1R. Venkata Neeraj Kumar and 2R. Sreenivasulu 1Department of Electrical Engineering, Indian Institute of Technology, Gandhinagar, Gujarat, India 2R.V.R.&J.C. College of Engineering (Autonomous), Chowdavaram, Guntur Andhra Pradesh, India Article history Abstract: Present global engineering professionals feels that, robotics is a Received: 20-07-2019 somewhat young field with extremely ruthless target, the crucial one being Revised: 06-08-2019 the making of machinery/equipment that can perform and feel like human Accepted: 22-08-2019 beings. Robot kinematics deals with the study of motion of linkages which includes displacement, velocities and accelerations of a robot manipulator Corresponding Author: analytically. Deriving the proper kinematic models for an open chain Dr. R. Sreenivasulu R.V.R.&J.C. College of mechanism of a robot is essential for analyzing the performance of industrial Engineering (Autonomous), robotic manipulators. In this study, first scrutinize a popular class of two and Chowdavaram, Guntur Andhra three degrees of freedom open chain mechanism whose inverse kinematics Pradesh, India admits a closed-form analytic solution. A simple coding was developed in Email: [email protected] python in an easy way. In this connection a two link planer manipulator was considered to get inverse kinematic solution developed in python environment. For this task, we present a solution for obtaining the joint variables of linkages to reach the position in a work space with the corresponding input values such as link lengths and position of end effector. Keywords: Robotic Manipulator, Inverse Kinematics, Joint Variables, PYTHON Introduction (1989) were used MACSYMA, REDUCE, SMP and SEGM methods, these methods requires typical Robot kinematics deals with the study of motion of mathematical concepts to achieve forward and inverse linkages which includes displacement, velocities and solutions.
    [Show full text]
  • Inverse Kinematics Problems with Exact Hessian Matrices
    Inverse Kinematics Problems with Exact Hessian Matrices Kenny Erleben Sheldon Andrews University of Copenhagen École de technologie supérieure [email protected] [email protected] ABSTRACT Popular techniques for solving IK problems typically discount Inverse kinematics (IK) is a central component of systems for mo- the use of exact Hessians, and prefer to rely on approximations of tion capture, character animation, motion planning, and robotics second-order derivatives. However, robotics work has shown that control. The eld of computer graphics has developed fast station- exact Hessians in 2D Lie algebra-based dynamical computations ary point solvers methods, such as the Jacobian transpose method outperforms approximate methods [Lee et al. 2005]. Encouraged by and cyclic coordinate descent. Much work with Newton methods these results, we examine the viability of exact Hessians for inverse focus on avoiding directly computing the Hessian, and instead ap- kinematics of 3D characters. To our knowledge, no previous work in proximations are sought, such as in the BFGS class of solvers. This computer graphics has addressed the signicance of using a closed paper presents a numerical method for computing the exact Hes- form solution for the exact Hessian, which is surprising since IK is sian of an IK system with spherical joints. It is applicable to human pertinent for many computer animation applications and there is a skeletons in computer animation applications and some, but not large body of work on the topic. all, robots. Our results show that using exact Hessians can give This paper presents the closed form solution in a simple and easy performance advantages and higher accuracy compared to standard to evaluate geometric form using two world space cross-products.
    [Show full text]
  • 3D Game Animation Software Free
    3d game animation software free click here to download Autodesk provides 3D animation software that spans the 3D production pipeline for today's demanding film, game, and television projects. An open-source professional free 3D animation software, Blender is used This 3D animation software lets you make a movie inside the game. With this 3D animation software, you are able to animate 3D characters in real- time that are especially suitable for game development and. Home of the Blender project - Free and Open 3D Creation Software. It supports the entirety of the 3D pipeline—modeling, rigging, animation, simulation, students, VFX experts, animators, game artists, modders, and the list goes on. Just look at how Pixar has changed the animation game: With 's “Toy 2. K- 3D. k3d best free animation software. Image courtesy of K-3D. You're basically asking: “What software should I use if I want to make a game? Blender is free, has a bunch of features, and does have in the options menu to If you have any particular question about 3D Animations we will be more than. We bring you the best 3D modelling software for every skill level. software; and on the next you'll find the best free 3D modelling software. Used by many leading VFX and animation studios, including Pixar, Maya's robust. Free and safe download. A 3D animation software that's like a game to make cool animations, easy to use; CONS: There is a free trial but the software itself. However, there is also a number of free 3D software suites out there for starting point for anyone looking to learn how to model for animation, film, and games.
    [Show full text]
  • Kinematics of Robots
    Kinematics of Robots Alba Perez Gracia c Draft date September 9, 2011 24 Chapter 2 Robot Kinematics Using Matrix Algebra 2.1 Overview In Chapter 1 we characterized the motion using vector and matrix algebra. In this chapter we introduce the application of 4 × 4 homogeneous transforms in traditional robot analysis, where the motion of a robot is described as a 4 × 4 homogoeneous matrix representing the position of the end-effector. This matrix is constructed as the composition of a series of local displacements along the chain. In this chapter we will learn how to calculate the forward and inverse kinematics of serial robots by using the Denavit-Hartenberg parameters to create the 4 × 4 homogeneous matrices. 2.2 Robot Kinematics From a kinematics point of view, a robot can be defined as a mechanical system that can be programmed to perform a number of tasks involving movement under automatic control. The main characteristic of a robot is its capability of movement in a six-dimensional space that includes translational and rotational coordinates. We model any mechanical system, including robots, as a series of rigid links connected by joints. The joints restrict the relative movement of adjacent links, and are generally powered and equipped with systems to sense this movement. 25 26 CHAPTER 2. ROBOT KINEMATICS USING MATRIX ALGEBRA The degrees of freedom of the robot, also called mobility, are defined as the number of independent parameters needed to specify the positions of all members of the system relative to a base frame. The most commonly used criteria to find the mobility of mechanisms is the Kutzbach-Gruebler formula.
    [Show full text]
  • An Overview Study of Game Engines
    Faizi Noor Ahmad Int. Journal of Engineering Research and Applications www.ijera.com ISSN : 2248-9622, Vol. 3, Issue 5, Sep-Oct 2013, pp.1673-1693 RESEARCH ARTICLE OPEN ACCESS An Overview Study of Game Engines Faizi Noor Ahmad Student at Department of Computer Science, ACNCEMS (Mahamaya Technical University), Aligarh-202002, U.P., India ABSTRACT We live in a world where people always try to find a way to escape the bitter realities of hubbub life. This escapism gives rise to indulgences. Products of such indulgence are the video games people play. Back in the past the term ―game engine‖ did not exist. Back then, video games were considered by most adults to be nothing more than toys, and the software that made them tick was highly specialized to both the game and the hardware on which it ran. Today, video game industry is a multi-billion-dollar industry rivaling even the Hollywood. The software that drives these three dimensional worlds- the game engines-have become fully reusable software development kits. In this paper, I discuss the specifications of some of the top contenders in video game engines employed in the market today. I also try to compare up to some extent these engines and take a look at the games in which they are used. Keywords – engines comparison, engines overview, engines specification, video games, video game engines I. INTRODUCTION 1.1.2 Artists Back in the past the term ―game engine‖ did The artists produce all of the visual and audio not exist. Back then, video games were considered by content in the game, and the quality of their work can most adults to be nothing more than toys, and the literally make or break a game.
    [Show full text]
  • 18-Animation.Pdf
    Advertisement Computer Animation Adam Finkelstein Princeton University COS 426, Spring 2003 Computer Animation 3-D and 2-D animation • What is animation? o Make objects change over time according to scripted actions • What is simulation? Pixar o Predict how objects change over time according to physical laws Homer 3-D Homer 2-D University of Illinois Outline Principles of Traditional Animation • Principles of animation • Squash and stretch • Keyframe animation • Slow In and out • Anticipation • Articulated figures • Exaggeration • Kinematics • Follow through and overlapping action • Timing •Dynamics • Staging • Straight ahead action and pose-to-pose action •Arcs • Secondary action • Appeal Angel Plate 1 Disney 1 Principles of Traditional Animation Principles of Traditional Animation • Squash and stretch • Slow In and Out Lasseter `87 Watt Figure 13.5 Principles of Traditional Animation Principles of Traditional Animation • Anticipation (and squash & stretch) • Squash and stretch • Slow In and out • Anticipation • Exaggeration • Follow through and overlapping action • Timing • Staging • Straight ahead action and pose-to-pose action •Arcs • Secondary action • Appeal Lasseter `87 Disney Computer Animation Keyframe Animation Animation pipeline • Define character poses at specific time steps o 3D modeling called “keyframes” o Articulation o Motion specification o Motion simulation o Shading o Lighting o Rendering o Postprocessing » Compositing Pixar Lasseter `87 2 Keyframe Animation Keyframe Animation • Interpolate variables describing keyframes
    [Show full text]
  • Kinematics for Lynxmotion Robot Arm Dr
    Kinematics for Lynxmotion Robot Arm Dr. Rainer Hessmer, October 2009 Note: This article contains text and two graphics from the reference [1] listed at the end. Kinematics Forward Kinematics Given the joint angles and the links geometry, compute the orientation of the end effector relative to the base frame. Inverse Kinematics Given the position and orientation of the end effector relative to the base frame compute all possible sets of joint angles and link geometries which could be used to attain the given position and orientation of the end effector. 2R Planar Manipulator Figure 1: Elbow up (a) and Elbow down (b) configuration of a 2R planar manipulator Forward Kinematics = x l1 cos 1 l 2 cos 1 2 = ⋅ y l1 sin 1 l2 sin 1 2 Inverse Kinematics 2 2 = 2 2 2 2 x y l1 cos 1 l2 cos 1 2 2l1 l2 cos 1 cos 1 2 2 2 2 2 l1 sin 1 l2 sin 1 2 2 l1 l2 sin 1 sin 1 2 = 2 2 [ ] l1 l2 2 l1 l2 cos 1 cos 1 2 sin 1 sin 1 2 Next we use the following equalities: sin x± y = sin x cos y ± cos xsin y cos x± y = cos x cos y ∓ sin x sin y Therefore 2 2 = 2 2 [ − ] x y l1 l 2 2l1 l2 cos 1 cos 1 cos 2 sin 1 sin 2 sin 1 sin 1 cos 2 cos 1 sin 2 = 2 2 [ 2 2 ] l1 l2 2 l1 l2 cos 1 cos 2 sin 2 cos 2 = 2 2 l1 l2 2 l1 l2 cos 2 and 2 2− 2− 2 = x y l1 l 2 cos 2 2 l1 l2 From here we could get the angle directly using the arccose function but this function is very inaccurate for small angles.
    [Show full text]
  • Animation, Motion Capture, & Inverse Kinematics Last Time? Today
    Last Time? • Navier-Stokes Equations Animation, Motion Capture, • Conservation of & Inverse Kinematics Momentum & Mass • Incompressible Flow Today Keyframing • How do we animate? • Use spline curves to automate the in betweening – Keyframing – Good control – Less tedious than drawing every frame – Procedural Animation • Creating a good animation still requires considerable – Physically-Based Animation skill and talent – Motion Capture – Forward and Inverse Kinematics • Rigid Body Dynamics • Finite Element Method ACM © 1987 “Principles of traditional animation applied to 3D computer animation” Procedural Animation Physically-Based Animation • Describes the motion algorithmically, • Assign physical properties to objects as a function of small number of (masses, forces, inertial properties) parameters • Example: a clock with second, minute • Simulate physics by solving equations and hour hands • Realistic but difficult to control – express the clock motions in terms of a “seconds” variable – the clock is animated by varying the seconds parameter g • Example: A bouncing ball -kt – Abs(sin(ωt+θ0))*e “Interactive Manipulation of Rigid Body Simulations” SIGGRAPH 2000, Popović, Seitz, Erdmann, Popović & Witkin 1 Motion Capture Today • Optical markers, high-speed • How do we animate? cameras, triangulation – Keyframing → 3D position – Procedural Animation • Captures style, subtle nuances – Physically-Based Animation and realism at high-resolution – Motion Capture • You must observe someone do something – Forward and • Difficult (or impossible?) to edit mo-cap data Inverse Kinematics • Rigid Body Dynamics • Finite Element Method Articulated Models Skeleton Hierarchy • Articulated models: • Each bone transformation – rigid parts described relative – connected by joints to the parent in hips the hierarchy: • They can be animated by specifying the joint left-leg ... angles as functions of time.
    [Show full text]
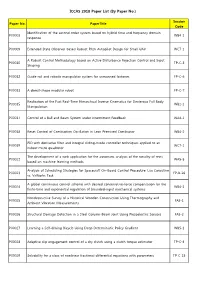
  • ICCAS 2018 Paper List (By Paper No.)
    ICCAS 2018 Paper List (By Paper No.) Session Paper No. PaperTitle Code Identification of the second order system based on hybrid time and frequency domain P00008 WB4-1 response P00009 Extended State Observer-based Robust Pitch Autopilot Design for Small UAV WC7-1 A Robust Control Methodology based on Active Disturbance Rejection Control and Input P00010 TP-C-3 Shaping P00012 Guide-rail and robotic manipulator system for unmanned factories FP-C-6 P00013 A donut-shape modular robot FP-C-7 Realization of the Fast Real-Time Hierarchical Inverse Kinematics for Dexterous Full Body P00015 WB2-1 Manipulation P00017 Control of a Ball and Beam System under Intermittent Feedback WA4-1 P00018 Reset Control of Combustion Oscillation in Lean Premixed Combustor WB4-2 PID with derivative filter and integral sliding-mode controller techniques applied to an P00019 WC7-2 indoor micro quadrotor The development of a web application for the automatic analysis of the tonality of texts P00022 WA5-5 based on machine learning methods Analysis of Scheduling Strategies for Spacecraft On-Board Control Procedure: Lua Coroutine P00023 FP-B-26 vs. VxWorks Task A global continuous control scheme with desired conservative-force compensation for the P00024 WB4-3 finite-time and exponential regulation of bounded-input mechanical systems Nondestructive Survey of a Historical Wooden Construction Using Thermography and P00025 FA5-1 Ambient Vibration Measurements P00026 Structural Damage Detection in a Steel Column-Beam Joint Using Piezoelectric Sensors FA5-2 P00027 Learning
    [Show full text]
  • Inverse Kinematics: a Review of Existing Techniques and Introduction of a New Fast Iterative Solver
    University of Cambridge Technical Report Inverse Kinematics: a review of existing techniques and introduction of a new fast iterative solver Andreas Aristidou and Joan Lasenby CUED/F-INFENG/TR-632 September 20, 2009 ⃝c Cambridge University Engineering Department Abstract Inverse Kinematics (IK) is defined as the problem of determining a set of appropriate joint configurations for which the end effectors move to desired positions as smoothly, rapidly, and as accurately as possible. During the last decades, several methods and techniques, sophisticated or heuristic, have been presented to produce fast and realistic solutions to the IK problem. However, most of the currently available methods suffer from high computational cost and production of unrealistic poses. This report reviews and compares the most popular IK meth- ods regarding reliability, computational cost and conversion criteria, with a novel heuristic and iterative method, called Forward And Backward Reaching Inverse Kinematics (FABRIK). FABRIK avoids the use of rotational angles or matrices, and instead finds each joint position via locating a point on a line. Thus, it converges in fewer iterations, has low computational cost and produces realistic poses. Constraints can easily be incorporated within the FABRIK methodology and multiple chains with multiple end effectors are also easily supported. i Acknowledgements We would like to thank Richard Wareham and Jonathan Cameron for introducing us to Blender and for their invaluable discussions and help with capturing data and producing video exam- ples. We are also very grateful to Charles Lee for his help with video processing and to Adam Becker for allowing us to use his voice as background to the videos.
    [Show full text]