Inverse Kinematics: a Review of Existing Techniques and Introduction of a New Fast Iterative Solver
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Randomized Path Planning for Redundant Manipulators Without Inverse Kinematics
Randomized Path Planning for Redundant Manipulators without Inverse Kinematics Mike Vande Weghe Dave Ferguson, Siddhartha S. Srinivasa Institute for Complex Engineered Systems Intel Research Pittsburgh Carnegie Mellon University 4720 Forbes Avenue Pittsburgh, PA 15213 Pittsburgh, PA 15213 [email protected] {dave.ferguson, siddhartha.srinivasa}@intel.com Abstract— We present a sampling-based path planning al- gorithm capable of efficiently generating solutions for high- dimensional manipulation problems involving challenging inverse kinematics and complex obstacles. Our algorithm extends the Rapidly-exploring Random Tree (RRT) algorithm to cope with goals that are specified in a subspace of the manipulator configuration space through which the search tree is being grown. Underspecified goals occur naturally in arm planning, where the final end effector position is crucial but the configuration of the rest of the arm is not. To achieve this, the algorithm bootstraps an optimal local controller based on the transpose of the Jacobian to a global RRT search. The resulting approach, known as Jacobian Transpose-directed Rapidly Exploring Random Trees (JT-RRTs), is able to combine the configuration space exploration of RRTs with a workspace goal bias to produce direct paths through complex environments extremely efficiently, without the need for any inverse kinematics. We compare our algorithm to a recently- developed competing approach and provide results from both simulation and a 7 degree-of-freedom robotic arm. I. INTRODUCTION Path planning for robotic systems operating in real envi- ronments is hard. Not only must such systems deal with the standard planning challenges of potentially high-dimensional and complex search spaces, but they must also cope with im- perfect information regarding their surroundings and perhaps Fig. -

A Closed-Form Solution for the Inverse Kinematics of the 2N-DOF Hyper-Redundant Manipulator Based on General Spherical Joint
applied sciences Article A Closed-Form Solution for the Inverse Kinematics of the 2n-DOF Hyper-Redundant Manipulator Based on General Spherical Joint Ya’nan Lou , Pengkun Quan, Haoyu Lin, Dongbo Wei and Shichun Di * School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150001, China; [email protected] (Y.L.); [email protected] (P.Q.); [email protected] (H.L.); [email protected] (D.W.) * Correspondence: [email protected]; Tel.: +86-1390-4605-946 Abstract: This paper presents a closed-form inverse kinematics solution for the 2n-degree of freedom (DOF) hyper-redundant serial manipulator with n identical universal joints (UJs). The proposed algorithm is based on a novel concept named as general spherical joint (GSJ). In this work, these universal joints are modeled as general spherical joints through introducing a virtual revolution between two adjacent universal joints. This virtual revolution acts as the third revolute DOF of the general spherical joint. Remarkably, the proposed general spherical joint can also realize the decoupling of position and orientation just as the spherical wrist. Further, based on this, the universal joint angles can be solved if all of the positions of the general spherical joints are known. The position of a general spherical joint can be determined by using three distances between this unknown general spherical joint and another three known ones. Finally, a closed-form solution for the whole manipulator is solved by applying the inverse kinematics of single general spherical joint section using these positions. Simulations are developed to verify the validity of the proposed closed-form inverse kinematics model. -

Inverse Kinematics (IK) Solution of a Robotic Manipulator Using PYTHON
Journal of Mechatronics and Robotics Original Research Paper Inverse Kinematics (IK) Solution of a Robotic Manipulator using PYTHON 1R. Venkata Neeraj Kumar and 2R. Sreenivasulu 1Department of Electrical Engineering, Indian Institute of Technology, Gandhinagar, Gujarat, India 2R.V.R.&J.C. College of Engineering (Autonomous), Chowdavaram, Guntur Andhra Pradesh, India Article history Abstract: Present global engineering professionals feels that, robotics is a Received: 20-07-2019 somewhat young field with extremely ruthless target, the crucial one being Revised: 06-08-2019 the making of machinery/equipment that can perform and feel like human Accepted: 22-08-2019 beings. Robot kinematics deals with the study of motion of linkages which includes displacement, velocities and accelerations of a robot manipulator Corresponding Author: analytically. Deriving the proper kinematic models for an open chain Dr. R. Sreenivasulu R.V.R.&J.C. College of mechanism of a robot is essential for analyzing the performance of industrial Engineering (Autonomous), robotic manipulators. In this study, first scrutinize a popular class of two and Chowdavaram, Guntur Andhra three degrees of freedom open chain mechanism whose inverse kinematics Pradesh, India admits a closed-form analytic solution. A simple coding was developed in Email: [email protected] python in an easy way. In this connection a two link planer manipulator was considered to get inverse kinematic solution developed in python environment. For this task, we present a solution for obtaining the joint variables of linkages to reach the position in a work space with the corresponding input values such as link lengths and position of end effector. Keywords: Robotic Manipulator, Inverse Kinematics, Joint Variables, PYTHON Introduction (1989) were used MACSYMA, REDUCE, SMP and SEGM methods, these methods requires typical Robot kinematics deals with the study of motion of mathematical concepts to achieve forward and inverse linkages which includes displacement, velocities and solutions. -

Inverse Kinematics Problems with Exact Hessian Matrices
Inverse Kinematics Problems with Exact Hessian Matrices Kenny Erleben Sheldon Andrews University of Copenhagen École de technologie supérieure [email protected] [email protected] ABSTRACT Popular techniques for solving IK problems typically discount Inverse kinematics (IK) is a central component of systems for mo- the use of exact Hessians, and prefer to rely on approximations of tion capture, character animation, motion planning, and robotics second-order derivatives. However, robotics work has shown that control. The eld of computer graphics has developed fast station- exact Hessians in 2D Lie algebra-based dynamical computations ary point solvers methods, such as the Jacobian transpose method outperforms approximate methods [Lee et al. 2005]. Encouraged by and cyclic coordinate descent. Much work with Newton methods these results, we examine the viability of exact Hessians for inverse focus on avoiding directly computing the Hessian, and instead ap- kinematics of 3D characters. To our knowledge, no previous work in proximations are sought, such as in the BFGS class of solvers. This computer graphics has addressed the signicance of using a closed paper presents a numerical method for computing the exact Hes- form solution for the exact Hessian, which is surprising since IK is sian of an IK system with spherical joints. It is applicable to human pertinent for many computer animation applications and there is a skeletons in computer animation applications and some, but not large body of work on the topic. all, robots. Our results show that using exact Hessians can give This paper presents the closed form solution in a simple and easy performance advantages and higher accuracy compared to standard to evaluate geometric form using two world space cross-products. -

3D Game Animation Software Free
3d game animation software free click here to download Autodesk provides 3D animation software that spans the 3D production pipeline for today's demanding film, game, and television projects. An open-source professional free 3D animation software, Blender is used This 3D animation software lets you make a movie inside the game. With this 3D animation software, you are able to animate 3D characters in real- time that are especially suitable for game development and. Home of the Blender project - Free and Open 3D Creation Software. It supports the entirety of the 3D pipeline—modeling, rigging, animation, simulation, students, VFX experts, animators, game artists, modders, and the list goes on. Just look at how Pixar has changed the animation game: With 's “Toy 2. K- 3D. k3d best free animation software. Image courtesy of K-3D. You're basically asking: “What software should I use if I want to make a game? Blender is free, has a bunch of features, and does have in the options menu to If you have any particular question about 3D Animations we will be more than. We bring you the best 3D modelling software for every skill level. software; and on the next you'll find the best free 3D modelling software. Used by many leading VFX and animation studios, including Pixar, Maya's robust. Free and safe download. A 3D animation software that's like a game to make cool animations, easy to use; CONS: There is a free trial but the software itself. However, there is also a number of free 3D software suites out there for starting point for anyone looking to learn how to model for animation, film, and games. -

Inverse Kinematics and Geometric Constraints for Articulated Fig
INVERSE KINEMATICS AND GEOMETRIC CONSTRAINTS FOR ARTICULATED FIGURE MANIPULATION by Chris Welman BSc Simon Fraser University a thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in the Scho ol of Computing Science c Chris Welman SIMON FRASER UNIVERSITY Septemb er All rights reserved This work may not b e repro duced in whole or in part by photo copy or other means without the p ermission of the author APPROVAL Name Chris Welman Degree Master of Science Title of thesis Inverse Kinematics and Geometric Constraints for Articulated Fig ure Manipulation Examining Committee Dr L Hafer Chair Dr TW Calvert Senior Sup ervisor Dr J Dill Dr D Forsey External Examiner Date Approved ii Abstract Computer animation of articulated gures can b e tedious largely due to the amount of data which must b e sp ecied at each frame Animation techniques range from simple interp olation b etween keyframed gure p oses to higherlevel algorithmic mo dels of sp ecic movement patterns The former provides the animator with complete control over the movement whereas the latter may provide only limited control via some highlevel parameters incorp orated into the mo del Inverse kinematic techniques adopted from the rob otics literature have the p otential to relieve the animator of detailed sp ecication of every motion parameter within a gure while retaining complete control over the movement if desired This work investigates the use of inverse kinematics and simple geometric constraints as to ols for the animator Previous -

Kinematics of Robots
Kinematics of Robots Alba Perez Gracia c Draft date September 9, 2011 24 Chapter 2 Robot Kinematics Using Matrix Algebra 2.1 Overview In Chapter 1 we characterized the motion using vector and matrix algebra. In this chapter we introduce the application of 4 × 4 homogeneous transforms in traditional robot analysis, where the motion of a robot is described as a 4 × 4 homogoeneous matrix representing the position of the end-effector. This matrix is constructed as the composition of a series of local displacements along the chain. In this chapter we will learn how to calculate the forward and inverse kinematics of serial robots by using the Denavit-Hartenberg parameters to create the 4 × 4 homogeneous matrices. 2.2 Robot Kinematics From a kinematics point of view, a robot can be defined as a mechanical system that can be programmed to perform a number of tasks involving movement under automatic control. The main characteristic of a robot is its capability of movement in a six-dimensional space that includes translational and rotational coordinates. We model any mechanical system, including robots, as a series of rigid links connected by joints. The joints restrict the relative movement of adjacent links, and are generally powered and equipped with systems to sense this movement. 25 26 CHAPTER 2. ROBOT KINEMATICS USING MATRIX ALGEBRA The degrees of freedom of the robot, also called mobility, are defined as the number of independent parameters needed to specify the positions of all members of the system relative to a base frame. The most commonly used criteria to find the mobility of mechanisms is the Kutzbach-Gruebler formula. -

An Overview Study of Game Engines
Faizi Noor Ahmad Int. Journal of Engineering Research and Applications www.ijera.com ISSN : 2248-9622, Vol. 3, Issue 5, Sep-Oct 2013, pp.1673-1693 RESEARCH ARTICLE OPEN ACCESS An Overview Study of Game Engines Faizi Noor Ahmad Student at Department of Computer Science, ACNCEMS (Mahamaya Technical University), Aligarh-202002, U.P., India ABSTRACT We live in a world where people always try to find a way to escape the bitter realities of hubbub life. This escapism gives rise to indulgences. Products of such indulgence are the video games people play. Back in the past the term ―game engine‖ did not exist. Back then, video games were considered by most adults to be nothing more than toys, and the software that made them tick was highly specialized to both the game and the hardware on which it ran. Today, video game industry is a multi-billion-dollar industry rivaling even the Hollywood. The software that drives these three dimensional worlds- the game engines-have become fully reusable software development kits. In this paper, I discuss the specifications of some of the top contenders in video game engines employed in the market today. I also try to compare up to some extent these engines and take a look at the games in which they are used. Keywords – engines comparison, engines overview, engines specification, video games, video game engines I. INTRODUCTION 1.1.2 Artists Back in the past the term ―game engine‖ did The artists produce all of the visual and audio not exist. Back then, video games were considered by content in the game, and the quality of their work can most adults to be nothing more than toys, and the literally make or break a game. -

18-Animation.Pdf
Advertisement Computer Animation Adam Finkelstein Princeton University COS 426, Spring 2003 Computer Animation 3-D and 2-D animation • What is animation? o Make objects change over time according to scripted actions • What is simulation? Pixar o Predict how objects change over time according to physical laws Homer 3-D Homer 2-D University of Illinois Outline Principles of Traditional Animation • Principles of animation • Squash and stretch • Keyframe animation • Slow In and out • Anticipation • Articulated figures • Exaggeration • Kinematics • Follow through and overlapping action • Timing •Dynamics • Staging • Straight ahead action and pose-to-pose action •Arcs • Secondary action • Appeal Angel Plate 1 Disney 1 Principles of Traditional Animation Principles of Traditional Animation • Squash and stretch • Slow In and Out Lasseter `87 Watt Figure 13.5 Principles of Traditional Animation Principles of Traditional Animation • Anticipation (and squash & stretch) • Squash and stretch • Slow In and out • Anticipation • Exaggeration • Follow through and overlapping action • Timing • Staging • Straight ahead action and pose-to-pose action •Arcs • Secondary action • Appeal Lasseter `87 Disney Computer Animation Keyframe Animation Animation pipeline • Define character poses at specific time steps o 3D modeling called “keyframes” o Articulation o Motion specification o Motion simulation o Shading o Lighting o Rendering o Postprocessing » Compositing Pixar Lasseter `87 2 Keyframe Animation Keyframe Animation • Interpolate variables describing keyframes -

Kinematics for Lynxmotion Robot Arm Dr
Kinematics for Lynxmotion Robot Arm Dr. Rainer Hessmer, October 2009 Note: This article contains text and two graphics from the reference [1] listed at the end. Kinematics Forward Kinematics Given the joint angles and the links geometry, compute the orientation of the end effector relative to the base frame. Inverse Kinematics Given the position and orientation of the end effector relative to the base frame compute all possible sets of joint angles and link geometries which could be used to attain the given position and orientation of the end effector. 2R Planar Manipulator Figure 1: Elbow up (a) and Elbow down (b) configuration of a 2R planar manipulator Forward Kinematics = x l1 cos 1 l 2 cos 1 2 = ⋅ y l1 sin 1 l2 sin 1 2 Inverse Kinematics 2 2 = 2 2 2 2 x y l1 cos 1 l2 cos 1 2 2l1 l2 cos 1 cos 1 2 2 2 2 2 l1 sin 1 l2 sin 1 2 2 l1 l2 sin 1 sin 1 2 = 2 2 [ ] l1 l2 2 l1 l2 cos 1 cos 1 2 sin 1 sin 1 2 Next we use the following equalities: sin x± y = sin x cos y ± cos xsin y cos x± y = cos x cos y ∓ sin x sin y Therefore 2 2 = 2 2 [ − ] x y l1 l 2 2l1 l2 cos 1 cos 1 cos 2 sin 1 sin 2 sin 1 sin 1 cos 2 cos 1 sin 2 = 2 2 [ 2 2 ] l1 l2 2 l1 l2 cos 1 cos 2 sin 2 cos 2 = 2 2 l1 l2 2 l1 l2 cos 2 and 2 2− 2− 2 = x y l1 l 2 cos 2 2 l1 l2 From here we could get the angle directly using the arccose function but this function is very inaccurate for small angles. -

Animation, Motion Capture, & Inverse Kinematics Last Time? Today
Last Time? • Navier-Stokes Equations Animation, Motion Capture, • Conservation of & Inverse Kinematics Momentum & Mass • Incompressible Flow Today Keyframing • How do we animate? • Use spline curves to automate the in betweening – Keyframing – Good control – Less tedious than drawing every frame – Procedural Animation • Creating a good animation still requires considerable – Physically-Based Animation skill and talent – Motion Capture – Forward and Inverse Kinematics • Rigid Body Dynamics • Finite Element Method ACM © 1987 “Principles of traditional animation applied to 3D computer animation” Procedural Animation Physically-Based Animation • Describes the motion algorithmically, • Assign physical properties to objects as a function of small number of (masses, forces, inertial properties) parameters • Example: a clock with second, minute • Simulate physics by solving equations and hour hands • Realistic but difficult to control – express the clock motions in terms of a “seconds” variable – the clock is animated by varying the seconds parameter g • Example: A bouncing ball -kt – Abs(sin(ωt+θ0))*e “Interactive Manipulation of Rigid Body Simulations” SIGGRAPH 2000, Popović, Seitz, Erdmann, Popović & Witkin 1 Motion Capture Today • Optical markers, high-speed • How do we animate? cameras, triangulation – Keyframing → 3D position – Procedural Animation • Captures style, subtle nuances – Physically-Based Animation and realism at high-resolution – Motion Capture • You must observe someone do something – Forward and • Difficult (or impossible?) to edit mo-cap data Inverse Kinematics • Rigid Body Dynamics • Finite Element Method Articulated Models Skeleton Hierarchy • Articulated models: • Each bone transformation – rigid parts described relative – connected by joints to the parent in hips the hierarchy: • They can be animated by specifying the joint left-leg ... angles as functions of time. -
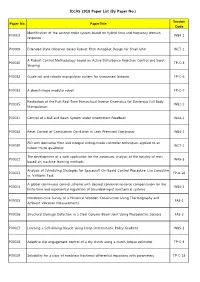
ICCAS 2018 Paper List (By Paper No.)
ICCAS 2018 Paper List (By Paper No.) Session Paper No. PaperTitle Code Identification of the second order system based on hybrid time and frequency domain P00008 WB4-1 response P00009 Extended State Observer-based Robust Pitch Autopilot Design for Small UAV WC7-1 A Robust Control Methodology based on Active Disturbance Rejection Control and Input P00010 TP-C-3 Shaping P00012 Guide-rail and robotic manipulator system for unmanned factories FP-C-6 P00013 A donut-shape modular robot FP-C-7 Realization of the Fast Real-Time Hierarchical Inverse Kinematics for Dexterous Full Body P00015 WB2-1 Manipulation P00017 Control of a Ball and Beam System under Intermittent Feedback WA4-1 P00018 Reset Control of Combustion Oscillation in Lean Premixed Combustor WB4-2 PID with derivative filter and integral sliding-mode controller techniques applied to an P00019 WC7-2 indoor micro quadrotor The development of a web application for the automatic analysis of the tonality of texts P00022 WA5-5 based on machine learning methods Analysis of Scheduling Strategies for Spacecraft On-Board Control Procedure: Lua Coroutine P00023 FP-B-26 vs. VxWorks Task A global continuous control scheme with desired conservative-force compensation for the P00024 WB4-3 finite-time and exponential regulation of bounded-input mechanical systems Nondestructive Survey of a Historical Wooden Construction Using Thermography and P00025 FA5-1 Ambient Vibration Measurements P00026 Structural Damage Detection in a Steel Column-Beam Joint Using Piezoelectric Sensors FA5-2 P00027 Learning