Howard Hathawy Aiken
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

The History of Computers: Part II
The History Of Computers: Part II You will learn about the computers of the 20th century and the people behind those machines. Some of the clipart images come from the sites: •http://www.clipartheaven.com/ •http://www.horton-szar.net/ •http://www.shootpetoet.be •www.dpw.wau.nl/pv/temp/ clipart/screenbeans.htm James Tam Categories Of 20th Century Computers •The mechanical monsters of the twenty first century - The machines of Konrad Zuse - The Bell telephone models - Howard Aiken and the Harvard computers •The computers of the electronic revolution -The ABC -The ENIAC - The Colossus machines of Bletchley Park •The first modern (stored program/memory) computers - The Manchester machine -The EDSAC - The EDVAC James Tam Computer History: Part II 1 The Mechanical Monsters •Performed calculations using moving mechanical parts rather than using electronics Images from the History of Computing Technology by Michael R. Williams James Tam The Mechanical Monsters •Many were used to solve equations that were either impossible or very time consuming to solve analytically. •Often conducting experiments were also impractical. James Tam Computer History: Part II 2 The Mechanical Monsters •Konrad Zuse -Z1 –Z4 •George Stibitz - Bell relay based computers Model I - VI •Howard Aiken - Harvard Mark I - IV James Tam The First Set Of Mechanical Monsters Were Created By Konrad Zuse •Developed a series of mechanical calculating machines (Z1, Z2, Z3, Z4). •Motivated by the need to perform complex calculations because current approaches were unsatisfactory. James Tam Computer History: Part II 3 The Z1 •It was entirely mechanical From the History of Computing Technology by Michael R. -

Copyrighted Material
1 The Function of Computation As in music theory, we cannot discuss the microprocessor without positioning it in the context of the history of the computer, since this component is the integrated version of the central unit. Its internal mechanisms are the same as those of supercomputers, mainframe computers and minicomputers. Thanks to advances in microelectronics, additional functionality has been integrated with each generation in order to speed up internal operations. A computer1 is a hardware and software system responsible for the automatic processing of information, managed by a stored program. To accomplish this task, the computer’s essential function is the transformation of data using computation, but two other functions are also essential. Namely, these are storing and transferring information (i.e. communication). In some industrial fields, control is a fourth function. This chapter focuses on the requirements that led to the invention of tools and calculating machines to arrive at the modern version of the computer that we know today. The technological aspect is then addressed. Some chronological references are given. Then several classification criteria are proposed. The analog computer, which is then described, was an alternative to the digital version. Finally, the relationship between hardware and software and the evolution of integration and its limits are addressed. NOTE.– This chapter does not attempt to replace a historical study. It gives only a few key dates and technical benchmarks to understand the technological evolution of the field. COPYRIGHTED MATERIAL 1 The French word ordinateur (computer) was suggested by Jacques Perret, professor at the Faculté des Lettres de Paris, in his letter dated April 16, 1955, in response to a question from IBM to name these machines; the English name was the Electronic Data Processing Machine. -

Open PDF in New Window
BEST AVAILABLE COPY i The pur'pose of this DIGITAL COMPUTER Itop*"°a""-'"""neesietter' YNEWSLETTER . W OFFICf OF NIVAM RUSEARCMI • MATNEMWTICAL SCIENCES DIVISION Vol. 9, No. 2 Editors: Gordon D. Goldstein April 1957 Albrecht J. Neumann TABLE OF CONTENTS It o Page No. W- COMPUTERS. U. S. A. "1.Air Force Armament Center, ARDC, Eglin AFB, Florida 1 2. Air Force Cambridge Research Center, Bedford, Mass. 1 3. Autonetics, RECOMP, Downey, Calif. 2 4. Corps of Engineers, U. S. Army 2 5. IBM 709. New York, New York 3 6. Lincoln Laboratory TX-2, M.I.T., Lexington, Mass. 4 7. Litton Industries 20 and 40 DDA, Beverly Hills, Calif. 5 8. Naval Air Test Centcr, Naval Air Station, Patuxent River, Maryland 5 9. National Cash Register Co. NC 304, Dayton, Ohio 6 10. Naval Air Missile Test Center, RAYDAC, Point Mugu, Calif. 7 11. New York Naval Shipyard, Brooklyn, New York 7 12. Philco, TRANSAC. Philadelphia, Penna. 7 13. Western Reserve Univ., Cleveland, Ohio 8 COMPUTING CENTERS I. Univ. of California, Radiation Lab., Livermore, Calif. 9 2. Univ. of California, SWAC, Los Angeles, Calif. 10 3. Electronic Associates, Inc., Princeton Computation Center, Princeton, New Jersey 10 4. Franklin Institute Laboratories, Computing Center, Philadelphia, Penna. 11 5. George Washington Univ., Logistics Research Project, Washington, D. C. 11 6. M.I.T., WHIRLWIND I, Cambridge, Mass. 12 7. National Bureau of Standards, Applied Mathematics Div., Washington, D.C. 12 8. Naval Proving Ground, Naval Ordnance Computation Center, Dahlgren, Virgin-.a 12 9. Ramo Wooldridge Corp., Digital Computing Center, Los Angeles, Calif. -

P the Pioneers and Their Computers
The Videotape Sources: The Pioneers and their Computers • Lectures at The Compp,uter Museum, Marlboro, MA, September 1979-1983 • Goal: Capture data at the source • The first 4: Atanasoff (ABC), Zuse, Hopper (IBM/Harvard), Grosch (IBM), Stibitz (BTL) • Flowers (Colossus) • ENIAC: Eckert, Mauchley, Burks • Wilkes (EDSAC … LEO), Edwards (Manchester), Wilkinson (NPL ACE), Huskey (SWAC), Rajchman (IAS), Forrester (MIT) What did it feel like then? • What were th e comput ers? • Why did their inventors build them? • What materials (technology) did they build from? • What were their speed and memory size specs? • How did they work? • How were they used or programmed? • What were they used for? • What did each contribute to future computing? • What were the by-products? and alumni/ae? The “classic” five boxes of a stored ppgrogram dig ital comp uter Memory M Central Input Output Control I O CC Central Arithmetic CA How was programming done before programming languages and O/Ss? • ENIAC was programmed by routing control pulse cables f ormi ng th e “ program count er” • Clippinger and von Neumann made “function codes” for the tables of ENIAC • Kilburn at Manchester ran the first 17 word program • Wilkes, Wheeler, and Gill wrote the first book on programmiidbBbbIiSiing, reprinted by Babbage Institute Series • Parallel versus Serial • Pre-programming languages and operating systems • Big idea: compatibility for program investment – EDSAC was transferred to Leo – The IAS Computers built at Universities Time Line of First Computers Year 1935 1940 1945 1950 1955 ••••• BTL ---------o o o o Zuse ----------------o Atanasoff ------------------o IBM ASCC,SSEC ------------o-----------o >CPC ENIAC ?--------------o EDVAC s------------------o UNIVAC I IAS --?s------------o Colossus -------?---?----o Manchester ?--------o ?>Ferranti EDSAC ?-----------o ?>Leo ACE ?--------------o ?>DEUCE Whirl wi nd SEAC & SWAC ENIAC Project Time Line & Descendants IBM 701, Philco S2000, ERA.. -

Computer Architecture ٤٠/٠٦/٢٦
Computer Architecture ٤٠/٠٦/٢٦ Computer Architecture Faculty Of Computers And Information Technology Second Term 2018 - 2019 Dr.Khaled Kh. Sharaf Computer Architecture Topic 1. Introduction 2. Performance Metrics I 3. Memory Hierarchy 4. MIPS Instruction Set Architecture (ISA) 5. Introduction to Logic Circuit Design 6. Instruction Level Parallelism 7. Multicore Architecture 8. GPU Architecture Textbook Patterson & Hennessy (2011 or 2013), "Computer Organization and Design: The Hardware/Software Interface“, revised 4th or 5th edition. ISBN: 978-0-12-374750-1 ١ Computer Architecture ٤٠/٠٦/٢٦ Computer Architecture 1.Introduction • Machine structures: layers of abstraction • Eight great ideas Computer Architecture Konrad Zuse’s Z3 electro-mechanical computer (1941, Germany). Turing complete, though conditional jumps were missing. ٢ Computer Architecture ٤٠/٠٦/٢٦ Computer Architecture Colossus (UK, 1941) was the world’s first totally electronic programmable computing device. But not Turing complete. Computer Architecture Harvard Mark I – IBM ASCC (1944, US). Electro- mechanical computer (no conditional jumps and not Turing complete). It could store 72 numbers, each 23 decimal digits long. It could do three additions or subtractions in a second. A multiplication took six seconds, a division took 15. 3 seconds, and a logarithm or a trigonometric function took over one minute. A loop was accomplished by joining the end of the paper tape containing the program back to the beginning of the tape (literally creating a loop). ٣ Computer Architecture ٤٠/٠٦/٢٦ Computer Architecture Electronic Numerical Integrator And Computer (ENIAC). The first general-purpose, electronic computer. It was a Turing-complete, digital computer capable of being reprogrammed and was running at 5,000 cycles per second for operations on the 10-digit numbers. -

ECE 252 / CPS 220 Advanced Computer Architecture I Lecture 1
ECE 552 / CPS 550 Advanced Computer Architecture I Lecture 2 History, Instruction Set Architectures Benjamin Lee Electrical and Computer Engineering Duke University www.duke.edu/~bcl15 www.duke.edu/~bcl15/class/class_ece252fall12.html ECE 552 Administrivia 11 September – Homework #1 Due Assignment on web page. Teams of 2-3. Submit soft copies to Sakai. Use Piazza for questions. 11 September – Class Discussion Do not wait until the day before! 1. Hill et al. “Classic machines: Technology, implementation, and economics” 2. Moore. “Cramming more components onto integrated circuits” 3. Radin. “The 801 minicomputer” 4. Patterson et al. “The case for the reduced instruction set computer” 5. Colwell et al. “Instruction sets and beyond: Computers, complexity, controversy” ECE 552 / CPS 550 2 A Bit of History Historical Narrative - Helps understand why ideas arose - Helps illustrate the design process Technology Trends - Future technologies may be as constrained as older ones Learning from History - Those who ignore history are doomed to repeat it - Every mistake made in mainframe design was also made in minicomputers, then microcomputers, where next? ECE 552 / CPS 550 3 Charles Babbage Charles Babbage (1791-1871) - Lucasian Professor of Mathematics - Cambridge University, 1827-1839 Contributions - Difference Engine 1823 - Analytic Engine 1833 Approach - mathematical tables (astronomy), nautical tables (navy) - any continuous function can be approximated by polynomial - mechanical gears and simple calculators ECE 552 / CPS 550 4 Difference Engine -

History in the Computing Curriculum
R e p o r t History in the Computing Curriculum I F I P TC 3 / TC 9 Joint Task Group John Impagliazzo (Task Group Chair) Hofstra University Martin Campbell-Kelly University of Warwick Gordon Davies Open University John A. N. Lee Virginia Tech Michael R. Williams University of Calgary Prepublication Copy 1998 October Copyright © 1998, 1999 Institute of Electrical and Electronics Engineers. This report is scheduled to appear in an upcoming issue of the Annals of the History of Computing. Internal or personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution must be obtained from the IEEE by sending an email request to <[email protected]>. HISTORY IN THE COMPUTING CURRICULUM Prepublication Copy 1998 October CONTENTS 1. INTRODUCTION 9. RESOURCES 9.1 Textbooks and General Works 2. GOALS AND OBJECTIVES 9.2 Monographs and Articles 9.3 Electronic Information 3. OVERVIEW OF THIS REPORT 9.4 Videos, Simulators, and Other Resources 4. BACKGROUND 10. EXTENDED TOPICS 4.1 Overview of Curriculum Recommendations 10.1 Advanced Courses 4.2 History Status 10.2 Projects 5. NEED FOR HISTORY CONTENT 11. CONCLUSIONS 5.1 The Student Perspective 5.2 The Professional Perspective 12. FUTURE DEVELOPMENTS 6. CURRICULUM CONTENT 6.1 Establishing a Knowledge Base ACKNOWLEDGMENTS 6.2 Methods of Presentation 6.2.1 The Period Method REFERENCES 6.2.2 Other Methods 6.3 Depth of Knowledge PUBLIC ACCESS 6.4 Clusters APPENDIX 7. IMPLEMENTATION OF A BASIC CURRICULUM A. -
Pioneercomputertimeline2.Pdf
Memory Size versus Computation Speed for various calculators and computers , IBM,ZQ90 . 11J A~len · W •• EDVAC lAS• ,---.. SEAC • Whirlwind ~ , • ENIAC SWAC /# / Harvard.' ~\ EDSAC Pilot• •• • ; Mc;rk I " • ACE I • •, ABC Manchester MKI • • ! • Z3 (fl. pt.) 1.000 , , .ENIAC •, Ier.n I i • • \ I •, BTL I (complexV • 100 ~ . # '-------" Comptometer • Ir.ne l ' with constants 10 0.1 1.0 10 100 lK 10K lOOK 1M GENERATIONS: II] = electronic-vacuum tube [!!!] = manual [1] = transistor Ime I = mechanical [1] = integrated circuit Iem I = electromechanical [I] = large scale integrated circuit CONTENTS THE COMPUTER MUSEUM BOARD OF DIRECTORS The Computer Museum is a non-profit. Kenneth H. Olsen. Chairman public. charitable foundation dedicated to Digital Equipment Corporation preserving and exhibiting an industry-wide. broad-based collection of the history of in Charles W Bachman formation processing. Computer history is Cullinane Database Systems A Compcmion to the Pioneer interpreted through exhibits. publications. Computer Timeline videotapes. lectures. educational programs. C. Gordon Bell and other programs. The Museum archives Digital Equipment Corporation I Introduction both artifacts and documentation and Gwen Bell makes the materials available for The Computer Museum 2 Bell Telephone Laboratories scholarly use. Harvey D. Cragon Modell Complex Calculator The Computer Museum is open to the public Texas Instruments Sunday through Friday from 1:00 to 6:00 pm. 3 Zuse Zl, Z3 There is no charge for admission. The Robert Everett 4 ABC. Atanasoff Berry Computer Museum's lecture hall and rece ption The Mitre Corporation facilities are available for rent on a mM ASCC (Harvard Mark I) prearranged basis. For information call C. -

The Z1: Architecture and Algorithms of Konrad Zuse's First Computer
The Z1: Architecture and Algorithms of Konrad Zuse’s First Computer Raul Rojas Freie Universität Berlin June 2014 Abstract This paper provides the first comprehensive description of the Z1, the mechanical computer built by the German inventor Konrad Zuse in Berlin from 1936 to 1938. The paper describes the main structural elements of the machine, the high-level architecture, and the dataflow between components. The computer could perform the four basic arithmetic operations using floating-point numbers. Instructions were read from punched tape. A program consisted of a sequence of arithmetical operations, intermixed with memory store and load instructions, interrupted possibly by input and output operations. Numbers were stored in a mechanical memory. The machine did not include conditional branching in the instruction set. While the architecture of the Z1 is similar to the relay computer Zuse finished in 1941 (the Z3) there are some significant differences. The Z1 implements operations as sequences of microinstructions, as in the Z3, but does not use rotary switches as micro- steppers. The Z1 uses a digital incrementer and a set of conditions which are translated into microinstructions for the exponent and mantissa units, as well as for the memory blocks. Microinstructions select one out of 12 layers in a machine with a 3D mechanical structure of binary mechanical elements. The exception circuits for mantissa zero, necessary for normalized floating-point, were lacking; they were first implemented in the Z3. The information for this article was extracted from careful study of the blueprints drawn by Zuse for the reconstruction of the Z1 for the German Technology Museum in Berlin, from some letters, and from sketches in notebooks. -

Computer Oral History Collection, 1969-1973, 1977
Computer Oral History Collection, 1969-1973, 1977 Interviewee: Association for Computing Machinery, General Meeting Participants: Walter Carlson, Henry Tropp, Ed Berkeley, Harry Hazen, Dick Clippinger, Betty Holberton, John Mauchly, Ross ?, Chuan Chu, Bob Campbell, Franz Alt, Tom ?, and Grace Murray Hopper Date: August 14, 1972 Repository: Archives Center, National Museum of American History CARLSON: …before the full event of the evening gets started. The first thing I would like to do, the important thing to do, is thank Honeywell for providing the equipment and staff to put this particular section on tape. We are very grateful for their participating with us in this event. The history project started in 1967 as a joint effort between AFIPS and The Smithsonian, and has been undertaken at various levels of activity since then, and is now at a vary high level of activity under Henry Tropp, who is the principal investigator at The Smithsonian, and will be sitting in this chair in my place a little later. The project at the moment is concentrating very heavily on the work that was done at the Bell Laboratories in the late ‘30s, work that was done at Harvard in the late ‘30s and early ‘40s, and the work that was done at NASA, at Iowa State, and at other locations. While that intensive research into those areas of activity is underway, we have been engaged in some events, if you will, among the people who had a lot to do with computer activities, and we’ve had one that some people in the room I recognize participated in out in the West Coast in December. -

Jacquard's Portrait a Logic Named Joe Harvard Mark I Manual Published Popular Mechanics Predicts Weight
out during parties to illustrate Calculator” which included the his plans for the Analytical earliest published examples of March Engine [Dec 23] (which would digital computer programs, in use punched cards). These this case for the Harvard Mark I soirees were held on Saturdays [Aug 7]. during the ‘season’ in London, Jacquard’s Portrait The report also represents the lasting from late March until the March 1840 end of July. We know that first extended analysis of programs since Ada Lovelace’s Babbage talked about the [Dec 10] “Sketch of the In Lyon, sometime during 1838, picture at one in March 1840, Analytical Engine Invented by Michel-Marie Carquillat wove a which is the reason for placing Charles Babbage . with Notes portrait of Joseph-Marie this entry here. Jacquard [July 7] in silk on a by the Translator” [July 10]. Jacquard loom. The machine Aiken liked to see himself as employed 24,000 cards, each Babbage’s successor, and the containing over 1000 holes. A Logic Named Joe document included a section March 1946 placing the Mark I in this historical context. Aiken had “A Logic Named Joe” is a sci-fi included something similar in short story by Murray Leinster his ASCC proposal [Jan 17]. published in the March 1946 issue of Astounding Science Hopper was the main author of Fiction. The story appeared chapters 1-3 and eight under Leinster’s real name, appendices. Chapters 4 and 5 William Fitzgerald Jenkins. were written by Aiken and Robert Campbell, and chapter 6, It details a world where containing directions for solving computers, called “Logics”, are sample problems on the connected to a vast repository of machine, was the work of data called the "tank". -
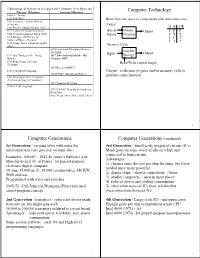
History of Computers
Chronological History of Pre and Early Computer Developments Computer Technology “Foreign” Milestones American Milestones 500 B. C. Abacus 1621 Slide Rule Built from two types of components plus interconnection: 1623 Schickard’s Adding Machine (Germany) Gates: 1642 Pascal’s Adding Machine (France) A B OR 1673 Leibniz Calculator (Germany) Binary Binary Output F F F 1804 Jacquard Loom and Punch Cards Inputs Function F T T 1822 Babbage’s Difference & T F T Analytical Engine (England) T T T 1850 George Boole’s Boolean Algebra (Irish) Memory Cells: 1890 Census and Tabulating Machines One Bit 1924 IBM Input Output 1937 Alan Turing and the Turing 1937 John Atanasoff and the ABC Storage Machine Computer (ISU) 1938 Konrad Zuse’s Z-series Read/Write control singal (Germany) 1939 Harvard MARK I 1943 COLOSSUS (England) Circuit - collection of gates and/or memory cells to 1945 ENIAC Mauchly and Eckert perform some function 1946 Manchester Mark I (England) (First Stored-Program Computer) 1947 Transistor Bell Labs EDSAC 1949 (England) . 1951 UNIVAC Mauchly/Eckert Sperry Rand Corp Grace Hopper wrote first compiler for it 1 2 Computer Generations Computer Generations (continued) 1st Generation - vacuum tubes with wires for 3rd Generation - Small-scale integrated circuits (ICs) interconnection (one gate per vacuum tube) Many gates on same wafer of silicon (chip) and connected to form circuits. Examples: ENIAC - 1943-46 Army’s Ballistics Lab Advantages: Mauchly/Eckert (U. of Penn.) 1st general-purpose 1) cheaper since the cost per chip the same, but fewer electronic digital computer needed since more powerful 30 tons, 15,000 sq.