RC30 Sound Rev 2
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Motorcycles and Related Spares & Memorabilia
The Autumn Stafford Sale The Classic Motorcycle Mechanics Show, Stafford | 13 & 14 October 2018 The Autumn Stafford Sale Important Pioneer, Vintage, Classic & Collectors’ Motorcycles and Related Spares & Memorabilia The 25th Carole Nash Classic Motorcycle Mechanics Show Sandylands Centre, Staffordshire County Showground | Saturday 13 & Sunday 14 October 2018 VIEWING BIDS ENQUIRIES CUSTOMER SERVICES Saturday 13 October Monday to Friday 8:30am - 6pm +44 (0) 20 7447 7447 James Stensel +44 (0) 20 7447 7447 9am to 5pm +44 (0) 20 7447 7401 fax +44 (0) 20 8963 2818 [email protected] +44 (0) 8700 273 625 fax Please see page 2 for bidder Sunday 14 October To bid via the internet please visit [email protected] from 9am information including after-sale www.bonhams.com collection and shipment Bill To SALE TIMES LIVE ONLINE BIDDING IS +44 (0) 20 8963 2822 Please see back of catalogue Saturday 13 October AVAILABLE FOR THIS SALE +44 (0) 8700 273 625 fax for important notice to bidders Spares & Memorabilia Please email [email protected] [email protected] (Lots 1 - 196) 12 noon with “Live bidding” in the subject line 48 hours before the auction Ben Walker IMPORTANT INFORMATION Followed by The Reed to register for this service +44 (0) 20 8963 2819 The United States Government Collection of Motorcycles +44 (0) 8700 273 625 fax has banned the import of ivory (Lots 201 - 242) 3pm Please note that bids should be [email protected] into the USA. Lots containing submitted no later than 4pm on ivory are indicated by the Sunday 14 October Friday 12 October. -

MARCA CC MODELO Acero Delt Acero Tras Kevlar Delt Kevlar Tras
MARCA CC MODELO Acero delt Acero Tras Kevlar delt Kevlar Tras Carbotec deCarbotec T HONDA 1300 CB 1300 03-06 86,90 € 37,28 € 116,99 € 54,13 € 138,00 € 62,95 € HONDA 100 CBR 1000 RR 04-07 83,93 € 112,78 € 54,13 € 138,00 € 62,95 € HONDA 1000 CBR 1000 RR 08-09 80,09 € 37,67 € 108,45 € 54,13 € 138,00 € 62,95 € HONDA 600 CBR 600 F 95-98 79,88 € 37,55 € 108,42 € 54,13 € 138,00 € 62,95 € HONDA 600 CBR 600 F 99-05 83,67 € 34,48 € 112,64 € 54,13 € 138,00 € 62,95 € HONDA 600 CBR 600 RR 03-06 80,13 € 35,71 € 105,32 € 54,13 € 138,00 € 62,95 € HONDA 600 CBR 600 RR 07-09 85,91 € 34,43 € 114,47 € 54,13 € 138,00 € 62,95 € HONDA 900 CBR 900 RR 00-01 80,38 € 38,91 € 107,84 € 54,13 € 138,00 € 62,95 € HONDA 900 CBR 900 RR 02-03 80,38 € 40,73 € 107,84 € 54,13 € 138,00 € 62,95 € HONDA 900 CBR 900 RR 96-99 78,48 € 38,41 € 106,46 € 54,13 € 138,00 € 62,95 € HONDA 600 Hornet 600 07-09 88,51 € 35,90 € 116,12 € 54,13 € 138,00 € 62,95 € HONDA 600 Hornet 600/S 04-06 86,31 € 37,18 € 115,27 € 54,13 € 138,00 € 62,95 € HONDA 600 Hornet 600/S 98-03 87,28 € 39,86 € 115,51 € 54,13 € 138,00 € 62,95 € HONDA 600 Hornet 900 02-06 81,53 € 35,56 € 110,90 € 54,13 € 138,00 € 62,95 € HONDA 1000 VTR 1000 00-02 84,85 € 37,17 € 113,66 € 54,13 € 138,00 € 62,95 € HONDA 1000 VTR 1000 97-99 82,52 € 37,17 € 111,19 € 54,13 € 138,00 € 62,95 € HONDA 1000 VTR 1000 SP1 00-01 74,05 € 37,00 € 100,74 € 54,13 € 138,00 € 62,95 € HONDA 1000 VTR 1000 SP2 02-03 78,24 € 35,81 € 105,96 € 54,13 € 138,00 € 62,95 € KAWASAKI 600 ER 6F 06-08 77,59 € 44,40 € 105,82 € 54,13 € 138,00 € 62,95 € KAWASAKI 600 ER 6N -
Tamiya America, Inc. MAP Price List 01-21-2019 Item # Description Retail MAP 10204 Caterham Super Seven BDR $526.00 $420.80 1021
Tamiya America, Inc. MAP Price List 01-21-2019 Item # Description Retail MAP 10204 Caterham Super Seven BDR $526.00 $420.80 1021 TRF801 LW Diff Outdrive $13.50 $10.80 1022 TRF801X Front Shock Tower $30.00 $24.00 1025 TRF801 LW Differential Ring $35.00 $28.00 1028 RC 60D Type A Pre-Mounted $65.00 $52.00 1029 RC 60D Type A Pre-Mounted $65.00 $52.00 10304 JR Mini 4WD Double Sided Tape $2.90 $2.32 10305 JR Slide Damper Spring $2.20 $1.76 10306 JR Bushing (White, 8pcs) $1.50 $1.20 10307 JR 2mm Spring Washer $1.30 $1.04 10308 JR Aluminum Shaft Stopper $5.40 $4.32 10309 JR Mini 4WD 2mm Washer $1.30 $1.04 1031 RC F1 Tire Front (Soft) $30.00 $24.00 10310 JR Mini 4WD Circuit Jump Ramp $4.50 $3.60 10311 JR Mini 4WD PRO G-22 Gear $2.30 $1.84 10312 JR Mini 4WD G-18 Gear $2.10 $1.68 10313 JR Mini 4WD Home Circuit Joint $2.70 $2.16 10314 JR Mini 4WD 2x72mm Hex Shafts $2.50 $2.00 10315 1/72 Kawasaki Ki-61-Id Hien $41.00 $32.80 10316 1/72 Mitsubishi A6M5 (ZEKE) $30.00 $24.00 10317 Mitsubishi A6M5/5a (ZEKE) $55.00 $44.00 10318 RC TSU-03 Servo $30.00 $24.00 10319 JR Propeller Shaft C Set $1.40 $1.12 1032 RC F1 Tire Rear (Hard) $34.00 $27.20 1033 TCS Finals M-Chassis Tire Pack $48.00 $38.40 1034 2.4 GHZ 4-Channel Receiver $98.00 $78.40 1035 RC Solaris 36J Tire Set $94.00 $75.20 1036 RC M-Chassis Pre-Glued Tires $27.00 $21.60 12010 Datsun 240ZG $183.00 $146.40 12029 Williams FW14B Renault $213.00 $170.40 12032 Honda RA273 $128.00 $102.40 12036 Tyrrell P34 Six Wheeler $151.00 $120.80 12047 Enzo Ferrari $662.00 $529.60 12050 Porsche Carrera GT $723.00 $578.40 12053 Team Lotus Type 49B 1968 $142.00 $113.60 12506 Motorsports Team Set $54.00 $43.20 12616 Ferrari FXX PE Parts $15.50 $12.40 12617 SC430 PE Parts $18.00 $14.40 12618 Honda RC211V'06 Front Fork Set $38.00 $30.40 12621 1/48 Lockheed F-16 Detail Part $17.50 $14.00 12622 1/350 Crew Set (144 pcs) $14.50 $11.60 12623 1/24 Nissan GT-R Photo-Etched $20.00 $16.00 12624 1/48 Mitsubishi A6M Zero $15.00 $12.00 Page 1 Tamiya America, Inc. -

Model Builder December 1990
VORLD’&fo ( ’UBLICATI DECEM CANA] ■ F' P i l l ) [ ( d W1U rJ h Wu n h ) 0 71896 — ■ * ? VANGUARD W . Airtronics’ Vanguard VG7P 7 channel and unmatched value of our very popular Functional Feature Design. FM system incorporates advanced design Vanguard series. The Vanguard VG7P offers an array of features and super narrow band perform Comfortably designed for the serious sophisticated features usually found on ance at a very affordable price. sport or competitive flyer, the VG7P is more expensive systems including, Aileron Competitive In Every Way. ideal for all types of R/C models. Compat Rudder Coupling, Dual Rate Elevator and The VG7P combines all the craftsman ible with all Airtronics servos and Aileron Controls, Throttle ship and advanced component tech accessories, the VG7P is an excellent End Point Adjustment, nology of our most sophisticated R/C cost-effective alternative to more Adjustable Low Throttle system s, with the expensive seven Trim, Elevator Rap proven reliability channel radios. Mixing, Total Travel Adjustment on Aileron, Elevator, and Rudder. Other features include Ασ™ ΐί*ηΐΤΐ α,Τ [ ^ π High Quality Rechargeable Series fm systems * NiCd Batteries, a Trainer System, and Servo Reversing on All Channels. Available with a variety of servo options, the VG7P offers Proportional Auxiliary Channel, Expanded Scale Voltmeter, High Quality Precision Gimbals, Electronic Trims, Three-Position Flap Switch, Adjustable Length and Tension Sticks. the VG7P also features a compact, Gold Label Super Narrow Band FM receiver with Surface Mount Technology for reliable, efficient operation in high interference environments. Exceptional Value For The Money. Airtronics now offers valueconscious modelers the perfect alternative to costly R/C system s. -

REC Catalogue
Race Engine Components Kingswood Farm, Competition Valve Specialists Kingswood Road, Design - Forging Albrighton, Wolverhampton, Machining - Heat Treatment WV7 3AQ Tel: +44 (0) 1902 373770 Fax: +44 (0) 1902 373772 Issue 29 E-Mail [email protected] Updated: 7th March 2020 Race Engine Components was established in 1962 and has had extensive race preparation and experience driving many British Sports Racing Cars of the era. Paul Ivey started his career as an apprentice at Downton Engineering and went from strength to strength from then on. He has been involved quite extensively with the development of the Cooper ‘S’, Jaguars and the Twin Cam Lotus engines of the time. Eventually this led him to the decision of starting up a special tuning parts business supplying valves to the fast growing car market. Inevitably this brought Race Engine Components and G&S Valves, the specialised engine valve manufacturer, together. They jointly formed a partnership in the early 80’s and together have developed many valve designs and associated parts including valves, retainers and collets suitable for the new breed of high revving racing engines that rev to speeds in excess of 16,000 rpm. G&S Valves Ltd. has itself serviced the race car and bike industry for over 65 years and together their valves have won at all levels of motor sport including F1, Sports Car, Le Mans, Indy Car, The TT, the World Super Sport 600 Class and many Club Level Championship Races. Both Race Engine Components and G&S valves go into 2011 with enthusiasm as always, and wish all their customers a winning season 1 of 86 Contents Car Valves 3 Bike Valves 25 Retainer 37 Valve Guides 41 Valve Springs & Seat Platforms 43 Crankshafts 44 GearBox Clusters 45 Cylinder Heads 45 Quick Reference:Valve Dimensions 46 Quick Reference: Part Number 62 Quick Reference: Retainers 83 Please note this is only a small percentage of our stock valves that we currently hold at Race Engine Components Ltd. -

THE AUTUMN STAFFORD SALE Sunday 15 October 2017 Staffordshire County Showground © Getty Images
THE AUTUMN STAFFORD SALE Sunday 15 October 2017 Staffordshire County Showground © Getty Images THE AUTUMN STAFFORD SALE Important Pioneer, Vintage, Classic & Collectors’ Motorcycles and Related Spares & Memorabilia Sunday 15 October 2017 at 10:30 The 24th Carole Nash Classic Motorcycle Mechanics Show Sandylands Centre Staffordshire County Showground VIEWING LIVE ONLINE BIDDING IS ENQUIRIES CUSTOMER SERVICES Saturday 14 October AVAILABLE FOR THIS SALE Monday to Friday 08:30 - 18:00 Ben Walker +44 (0) 20 7447 7447 10:00 to 17:00 Please email [email protected] +44 (0) 20 8963 2819 with “Live bidding” in the subject +44 (0) 8700 273 625 fax Please see page 2 for bidder Sunday 15 October line 48 hours before the auction [email protected] from 09:00 to register for this service information including after-sale collection and shipment James Stensel SALE TIMES Please note that bids should be +44 (0) 20 8963 2818 submitted no later than 16:00 on Please see back of catalogue Spares & Memorabilia 10.30 +44 (0) 8700 273 625 fax for important notice to bidders Motorcycles 11.30 Friday 13 October. Thereafter bids [email protected] should be sent directly to the Bonhams office at the sale venue. IMPORTANT INFORMATION SALE NUMBER Bill To 24131 +44 (0) 8700 270 089 fax or +44 (0) 20 8963 2822 The United States Government [email protected] +44 (0) 8700 273 625 fax has banned the import of ivory CATALOGUE: [email protected] into the USA. Lots containing We regret that we are unable to ivory are indicated by the £25.00 + p&p accept telephone bids for lots with Andy Barrett symbol Ф printed beside the a low estimate below £500. -

PMI Europe B.V. Powersports Pricelist (Effective June 1St 2015)
KRT Custom Speed GmbH Otterbacher Strasse 4, 4786 Brunnenthal Tel: +43 7712 296370, E-Mail: [email protected] PMI Europe B.V. Powersports Pricelist (effective June 1st 2015) Currency Euro Prices excluding VAT Effective from 1 June 2015 Valid to 31 December 2015 Note: PMI Europe B.V. reserves the right to change pricing at any time without prior notice New Nett Brand Part number Description Product Group price COMETIC B0230020RC Cometic Replacement Base Gasket for WC7171 120108 8,62 COMETIC B0402020RC Suzuk GSX1300R Busa '99-UP base 0.20" RC Gasket - 306597 120108 28,82 COMETIC B0933SP1010RC Cometic Base Gasket KTM 530 '08> 112mm ID bore. 0.10" 120108 9,81 COMETIC B0933SP1014RC Cometic Base Gasket KTM 530 '08> 112mm ID bore. 0.14" 120108 9,81 COMETIC B0933SP1020RC Cometic Base Gasket KTM 530 '08> 112mm ID bore. 0.20" 120108 9,81 COMETIC EC1232032AFM Cometic HONDA CBR600RR '07-14 Clutch cover gasket large 120108 21,22 COMETIC H0119SPB043C Cometic Head Gasket Honda CB750 2V '69-78 Cu 120108 60,18 COMETIC H0127043C Cometic Head Gasket Kawasaki KZ/GPZ/ZX750 Turbo Cu 69.00mm 120108 56,34 COMETIC H0321SP1043C Yamaha XT600 Copper head Gasket 103MM 0.43' 120108 32,35 COMETIC H0350SP7043C Cometic Head Gasket Kawasaki KZ900-1000 2Pcs. Cu 120108 68,38 COMETIC H0420SP2043F Cometic CFM Head Gasket Honda CB450/T500 Four '66-75 120108 49,03 COMETIC H0420SP8043C Cometic Head Copper Gasket Honda CB450/T500 Four '66-75 120108 56,34 COMETIC H0502SP3030S SUZUKI TL1000/SV1000 '98-03 103mm .030" MLS HEAD GASKETS(1pc 120108 41,12 COMETIC H0703SP1030S KAWASAKI -

CUP NOODLE HONDA NSR250 the Cowling of the Cup Noodle Sponsored Honda NSR250's Were Painted in Gold (No
ITEM 14061 The Honda Racing Corporation is well known for producing highly pressed crankshaft, rear-mounted carburetors with a throttle-sensing sophisticated, formidable racing motorcycles. Making its prototype system, and electronically controlled porting, known as the RC Valve debut in 1985 and designated the RS250RW, Honda's 250cc master- system, make it one of the most advanced liquid-cooled, two-stroke rac- piece achieved virtually instant fame. This bike stormed the 250cc rac- ing powerplants in the world. The exceptionally rigid frame is an alumi- ing scene by winning the 1985 World Grand Championship title, and num twin-spar type, as seen on competition machines. The rear swing has been in production as the NSR250 since then. It has, of course, un- arm is a triangulated box-section aluminum unit, which is damped by a dergone several advancements through the years, to keep pace with single shock absorber. Due to its excellent competitiveness, the NSR is the changing demands of Grand Prix racing, but it's much the same used by many teams racing in the Japanese 250cc motorcycle cham- bike. The design of its awesome powerplant was taken from the legenda- pionships, as well as the world racing scene. One such team is spon- ry NSR500 racer. With a displacement of 249cc, in a V-2 cylinder for- sored by the famous Cup Noodle firm. This NSR250 demonstrated su- mat, it is regarded by many motorsports enthusiasts as a split version of perb racing performance to thousands of Japanese racing fans through- the larger, V-4 cylinder, SOOcc engine. -
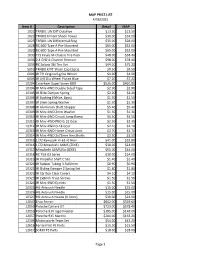
MAP PRICE LIST 4/06/2021 Item # Description Retail
MAP PRICE LIST 4/06/2021 Item # Description Retail MAP 1021 TRF801 LW Diff Outdrive $13.50 $13.50 1022 TRF801X Front Shock Tower $30.00 $24.00 1025 TRF801 LW Differential Ring $35.00 $28.00 1028 RC 60D Type A Pre-Mounted $65.00 $52.00 1029 RC 60D Type A Pre-Mounted $65.00 $52.00 1033 TCS Finals M-Chassis Tire Pack $48.00 $38.40 1034 2.4 GHZ 4-Channel Receiver $98.00 $78.40 1035 RC Solaris 36J Tire Set $94.00 $75.20 5010 TRF801X/XT Shock Cap (2pcs) $9.50 $9.50 6001 JR TPI Original Lg Dia Wheel $4.00 $4.00 6005 JR LHS Dia Wheel Plated Blue $7.20 $7.20 10204 Caterham Super Seven BDR $526.00 $420.80 10304 JR Mini 4WD Double Sided Tape $2.90 $2.90 10305 JR Slide Damper Spring $2.20 $2.20 10306 JR Bushing (White, 8pcs) $1.50 $1.50 10307 JR 2mm Spring Washer $1.30 $1.30 10308 JR Aluminum Shaft Stopper $5.40 $5.40 10309 JR Mini 4WD 2mm Washer $1.30 $1.30 10310 JR Mini 4WD Circuit Jump Ramp $4.50 $4.50 10311 JR Mini 4WD PRO G-22 Gear $2.30 $2.30 10312 JR Mini 4WD G-18 Gear $2.10 $2.10 10313 JR Mini 4WD Home Circuit Joint $2.70 $2.70 10314 JR Mini 4WD 2x72mm Hex Shafts $2.50 $2.50 10315 1/72 Kawasaki Ki-61-Id Hien $41.00 $32.80 10316 1/72 Mitsubishi A6M5 (ZEKE) $30.00 $24.00 10317 Mitsubishi A6M5/5a (ZEKE) $55.00 $44.00 10318 RC TSU-03 Servo $30.00 $24.00 10319 JR Propeller Shaft C Set $1.40 $1.40 10320 JR Rubber Tubing 3.5x60mm $0.90 $0.90 10321 JR Sliding Damper 2 Spring Set $1.80 $1.80 10322 JR Car Box Clear Covers $4.10 $4.10 10323 JR 2x8mm Truss Screws $1.50 $1.50 10324 JR Mini 4WD Eyelets $1.50 $1.50 10325 HG Airbrush Needle $15.00 $15.00 -

Birmingham, Alabama I October 6, 2018
Birmingham, Alabama I October 6, 2018 Birmingham, Alabama ︲ Saturday October 6, 2018 at 12pm and 1pm BONHAMS INQUIRIES Vehicle Documents 7601 W. Sunset Boulevard General Information Stanley Tam Los Angeles, California 90046 +1 (415) 391 4000 +1 (415) 503 3322 +1 (415) 391 4040 Fax +1 (415) 391 4040 Fax 580 Madison Avenue [email protected] [email protected] New York, New York 10022 Motorcycles West Coast BIDS Craig Mallery +1 (323) 850 7500 220 San Bruno Avenue +1 (323) 436 5470 +1 (323) 850 6090 San Francisco, California 94103 [email protected] [email protected] bonhams.com/barber David Edwards +1 (949) 460 3545 From October 3 to 8, to reach us at PREVIEW & AUCTION LOCATION [email protected] the Barber Museum: Barber Vintage +1 (415) 391 4000 Mark Osborne Motorsports Museum +1 (415) 391 4040 fax +1 (415) 518 0094 [email protected] 6030 Barber Motorsports Pkwy [email protected] Leeds, Alabama 35094 Lance Butler To bid via the internet please visit PLEASE SEE PAGE 6 FOR +1 (323) 940 8092 bonhams.com/barber IMPORTANT ENTRY INFORMATION [email protected] REGISTRATION IMPORTANT NOTICE PREVIEW Motorcycles East Coast Thursday October 4, 12pm to 5pm Please note that all customers, irrespective of Tim Parker any previous activity with Bonhams, are required Friday October 5, 8.30am to 5pm +1 (651) 235 2776 to complete the Bidder Registration Form in Saturday October 6, 8.30am to 12pm [email protected] advance of the sale. The form can be found at the back of every catalogue and on our website AUCTION TIMES Eric Minoff at www.bonhams.com and should be returned Saturday October 6 +1 (917) 206 1630 by email or post to the specialist department or to the bids department at [email protected] Memorabilia 12pm [email protected] Motorcycles 1pm Europe To bid live online and / or leave internet bids please go to www.bonhams.com/ Ben Walker 25100 auctions/25100 and click on the Register to bid AUCTION NUMBER: +44 (0) 20 8963 2819 Memorabilia: Lots 1 – 51 link at the top left of the page. -

OCTOBER 2019 NEWSLETTER PRESIDENT’S PREAMBLE - Bob Humphreys
OCTOBER NATIONALS CLUB MEETING RESULTS THIS INSIDE WEDNESDAY! OCTOBER 2019 NEWSLETTER PRESIDENT’S PREAMBLE - Bob Humphreys Well folks, the end of nearly two years of organisation, deliberation and a bit of anxiety thrown in, and we came up with a very successful Nationals! The weather Gods were with us all weekend. Just a bit of rain on Monday evening. Otherwise sunshine all the way. We had a lot of feedback from the spectators who said we had put on a great event, and we had quite a few visitors on the Friday and Saturday but on the Sunday they came in their hundreds! We took about $20,000 at the gate over the weekend, and the memorabilia stall (which was staffed by Haley and Steve - Michelle Gape’s daughter and SIL) were selling T-shirts, Polos and hats etc which went like hot cakes. Our visitors from Interstate enjoyed the new circuit and the hospitality and friendship offered to them by our members, a lot of camaraderie over the 4/5 days, many friendships were made and promises given to meet at the Island Classic in January! An unfortunate end to the day on Monday, with an oil spill (that’s racing for you), but safety for all was the ‘name of the game’ and accepted by all entrants as a sensible outcome. Our Trophies were well received, I felt they were up to National Standards. Many thanks to all our sponsors, especially our Major Sponsor Healthways, and Mick Murray and the local Dept.of Sport and recreation. Thanks again must go to all our magnificent volunteers and Marshals, and the members of the Indian Harley Club of Bunbury who did sterling work at the gate and car park etc. -

Wesfil Filter Catalog
Wesfil Filter Catalog Make MODEL YEAR AIR OIL FUEL CABIN NOTES AEC Most Models 1963-1978 WR2132P OEM: 78-891 Albion Most Models WR2132P OEM: 78-891 Alfa Romeo 147 1.6L, 2.0L 2001-01/11 WA1146 WCO51 IN TANK WACF0065 Twin Spark. Petrol. 4Cyl. AR32104/AR32310. DOHC 16V Alfa Romeo 147 1.9L JTD 2006-01/11 WCO51 WCF12 WACF0065 Turbo Diesel. 4Cyl. 937A5. CRD. DOHC 16V Alfa Romeo 147 3.2L V6 2003-2007 WA1147 WCO47 IN TANK WACF0065 GTA. Petrol. 932A0. MPFI. DOHC 24V Alfa Romeo 156 2.0L 1999-07/02 WA1147 WCO51 IN TANK WACF0065 Twin Spark. Petrol. 4Cyl. AR32301. MPFI. DOHC 16V Alfa Romeo 156 2.0L JTS 08/02-06/06 WA1147 WCO50 WZ469 WACF0065 Petrol. 4Cyl. 937A1. MPFI. DOHC 16V Alfa Romeo 156 2.5L V6 1999-05/06 WA1147 WCO51 IN TANK WACF0065 Petrol. AR3240. MPFI. DOHC 24V Alfa Romeo 156 3.2L V6 08/02-2005 WA1147 WCO47 IN TANK WACF0065 GTA. Petrol. 932A. MPFI. DOHC 24V Alfa Romeo 159 1.7L TBi 2010-on WA5291 WCO131 (C) IN TANK WACF0063 1750TBi. Petrol. 4Cyl. 939B1. DI. DOHC 16V Alfa Romeo 159 1.9L JTD 2007-12/10 WA5291 WCO70 (C) WCF228 WACF0063 Turbo Diesel. 4Cyl. 939A2. CRD. DOHC 16V Alfa Romeo 159 2.2L JTS 2006-10/10 WA5291 WCO32 (C) IN TANK WACF0063 Petrol. 4Cyl. 939A5. DI. DOHC 16V Alfa Romeo 159 2.4L JTD 2006-on WA5291 WCO120 (C) WCF228 WACF0063 Turbo Diesel. 5Cyl. 939A3. CRD. DOHC 20V Alfa Romeo 159 3.2L V6 2006-on WA5291 WCO4 (C) IN TANK WACF0063 Q4.