Efficient Sampling Rate Offset Compensation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Designing Commutative Cascades of Multidimensional Upsamplers And
IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 0 Designing Commutative Cascades of Multidimensional Upsamplers and Downsamplers Brian L. Evans, Member, IEEE Abstract In multiple dimensions, the cascade of an upsampler by L and a downsampler by L commutes if and only if the integer matrices L and M are right coprime and LM = ML. This pap er presents algorithms to design L and M that yield commutative upsampler/dowsampler cascades. We prove that commutativity is p ossible if the 1 Jordan canonical form of the rational resampling matrix R = LM is equivalent to the Smith-McMillan form of R. A necessary condition for this equivalence is that R has an eigendecomp osition and the eigenvalues are rational. B. L. Evans is with the Department of Electrical and Computer Engineering, The UniversityofTexas at Austin, Austin, TX 78712-1084, USA. E-mail: [email protected], Web: http://www.ece.utexas.edu/~b evans, Phone: 512 232-1457, Fax: 512 471-5907. This work was sp onsored in part by NSF CAREER Award under Grant MIP-9702707. July 31, 1997 DRAFT IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 1 I. Introduction 1 Resampling systems scale the sampling rate by a rational factor R = L=M = LM , or 1 equivalently decimate by H = M=L = L M [1], by essentially upsampling by L, ltering, and downsampling by M . In converting compact disc data sampled at 44.1 kHz to digital audio tap e 48000 Hz 160 data sampled at 48 kHz, R = = . Because we can always factor R into coprime 44100 Hz 147 integers L and M , we can always commute the upsampler and downsampler which leads to ecient p olyphase structures of the resampling system. -

Deep Image Prior for Undersampling High-Speed Photoacoustic Microscopy
Photoacoustics 22 (2021) 100266 Contents lists available at ScienceDirect Photoacoustics journal homepage: www.elsevier.com/locate/pacs Deep image prior for undersampling high-speed photoacoustic microscopy Tri Vu a,*, Anthony DiSpirito III a, Daiwei Li a, Zixuan Wang c, Xiaoyi Zhu a, Maomao Chen a, Laiming Jiang d, Dong Zhang b, Jianwen Luo b, Yu Shrike Zhang c, Qifa Zhou d, Roarke Horstmeyer e, Junjie Yao a a Photoacoustic Imaging Lab, Duke University, Durham, NC, 27708, USA b Department of Biomedical Engineering, Tsinghua University, Beijing, 100084, China c Division of Engineering in Medicine, Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Cambridge, MA, 02139, USA d Department of Biomedical Engineering and USC Roski Eye Institute, University of Southern California, Los Angeles, CA, 90089, USA e Computational Optics Lab, Duke University, Durham, NC, 27708, USA ARTICLE INFO ABSTRACT Keywords: Photoacoustic microscopy (PAM) is an emerging imaging method combining light and sound. However, limited Convolutional neural network by the laser’s repetition rate, state-of-the-art high-speed PAM technology often sacrificesspatial sampling density Deep image prior (i.e., undersampling) for increased imaging speed over a large field-of-view. Deep learning (DL) methods have Deep learning recently been used to improve sparsely sampled PAM images; however, these methods often require time- High-speed imaging consuming pre-training and large training dataset with ground truth. Here, we propose the use of deep image Photoacoustic microscopy Raster scanning prior (DIP) to improve the image quality of undersampled PAM images. Unlike other DL approaches, DIP requires Undersampling neither pre-training nor fully-sampled ground truth, enabling its flexible and fast implementation on various imaging targets. -

ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform
Department of Electrical Engineering University of Arkansas ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform Dr. Jingxian Wu [email protected] 2 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • DTFT of Sampled Signals • Upsampling and downsampling 3 DTFT • Discrete-time Fourier Transform (DTFT) X () x(n)e jn n – (radians): digital frequency • Review: Z-transform: X (z) x(n)zn n0 j X () X (z) | j – Replace z with e . ze • Review: Fourier transform: X () x(t)e jt – (rads/sec): analog frequency 4 DTFT • Relationship between DTFT and Fourier Transform – Sample a continuous time signal x a ( t ) with a sampling period T xs (t) xa (t) (t nT ) xa (nT ) (t nT ) n n – The Fourier Transform of ys (t) jt jnT X s () xs (t)e dt xa (nT)e n – Define: T • : digital frequency (unit: radians) • : analog frequency (unit: radians/sec) – Let x(n) xa (nT) X () X s T 5 DTFT • Relationship between DTFT and Fourier Transform (Cont’d) – The DTFT can be considered as the scaled version of the Fourier transform of the sampled continuous-time signal jt jnT X s () xs (t)e dt xa (nT)e n x(n) x (nT) T a jn X () X s x(n)e T n 6 DTFT • Discrete Frequency – Unit: radians (the unit of continuous frequency is radians/sec) – X ( ) is a periodic function with period 2 j2 n jn j2n jn X ( 2 ) x(n)e x(n)e e x(n)e X () n n n – We only need to consider for • For Fourier transform, we need to consider 1 – f T 2 2T 1 – f T 2 2T 7 DTFT • Example: find the DTFT of the following signal – 1. -
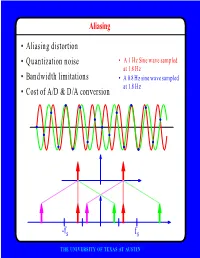
F • Aliasing Distortion • Quantization Noise • Bandwidth Limitations • Cost of A/D & D/A Conversion
Aliasing • Aliasing distortion • Quantization noise • A 1 Hz Sine wave sampled at 1.8 Hz • Bandwidth limitations • A 0.8 Hz sine wave sampled at 1.8 Hz • Cost of A/D & D/A conversion -fs fs THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Perfect reconstruction of a Better trade-off between signal is possible even after bandwidth and noise severe distortion immunity performance digital analog bandwidth Increase signal-to-noise ratio simply by adding more bits SNR = -7.2 + 6 dB/bit THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Programmability • Modifiable in the field • Implement multiple standards • Better user interfaces • Tolerance for changes in specifications • Get better use of hardware for low-speed operations • Debugging • User programmability THE UNIVERSITY OF TEXAS AT AUSTIN Disadvantages of Digital Systems Programmability • Speed is too slow for some applications • High average power and peak power consumption RISC (2 Watts) vs. DSP (50 mW) DATA PROG MEMORY MEMORY HARVARD ARCHITECTURE • Aliasing from undersampling • Clipping from quantization Q[v] v v THE UNIVERSITY OF TEXAS AT AUSTIN Analog-to-Digital Conversion 1 --- T h(t) Q[.] xt() yt() ynT() yˆ()nT Anti-Aliasing Sampler Quantizer Filter xt() y(nT) t n y(t) ^y(nT) t n THE UNIVERSITY OF TEXAS AT AUSTIN Resampling Changing the Sampling Rate • Conversion between audio formats Compact 48.0 Digital Disc ---------- Audio Tape 44.1 KHz44.1 48 KHz • Speech compression Speech 1 Speech for on DAT --- Telephone 48 KHz 6 8 KHz • Video format conversion -

JASON Manual
Weiss Engineering Ltd. Florastrasse 42, 8610 Uster, Switzerland www.weiss-highend.com JASON OWNERS MANUAL OWNERS MANUAL FOR WEISS JASON CD TRANSPORT INTRODUCTION Dear Customer Congratulations on your purchase of the JASON CD Transport and welcome to the family of Weiss equipment owners! The JASON is the result of an intensive research and development process. Research was conducted both in analog and digital circuit design, as well as in signal processing algorithm specification. On the following pages I will introduce you to our views on high quality audio processing. These include fundamental digital and analog audio concepts and the JASON CD Transport. I wish you a long-lasting relationship with your JASON. Yours sincerely, Daniel Weiss President, Weiss Engineering Ltd. Page: 2 Date: 03/13 /dw OWNERS MANUAL FOR WEISS JASON CD TRANSPORT TABLE OF CONTENTS 4 A short history of Weiss Engineering 5 Our mission and product philosophy 6 Advanced digital and analog audio concepts explained 6 Jitter Suppression, Clocking 8 Upsampling, Oversampling and Sampling Rate Conversion in General 11 Reconstruction Filters 12 Analog Output Stages 12 Dithering 14 The JASON CD Transport 14 Features 17 Operation 21 Technical Data 22 Contact Page: 3 Date: 03/13 /dw OWNERS MANUAL FOR WEISS JASON CD TRANSPORT A SHORT HISTORY OF WEISS ENGINEERING After studying electrical engineering, Daniel Weiss joined the Willi Studer (Studer - Revox) company in Switzerland. His work included the design of a sampling frequency converter and of digital signal processing electronics for digital audio recorders. In 1985, Mr. Weiss founded the company Weiss Engineering Ltd. From the outset the company concentrated on the design and manufacture of digital audio equipment for mastering studios. -

MULTIRATE SIGNAL PROCESSING Multirate Signal Processing
MULTIRATE SIGNAL PROCESSING Multirate Signal Processing • Definition: Signal processing which uses more than one sampling rate to perform operations • Upsampling increases the sampling rate • Downsampling reduces the sampling rate • Reference: Digital Signal Processing, DeFatta, Lucas, and Hodgkiss B. Baas, EEC 281 431 Multirate Signal Processing • Advantages of lower sample rates –May require less processing –Likely to reduce power dissipation, P = CV2 f, where f is frequently directly proportional to the sample rate –Likely to require less storage • Advantages of higher sample rates –May simplify computation –May simplify surrounding analog and RF circuitry • Remember that information up to a frequency f requires a sampling rate of at least 2f. This is the Nyquist sampling rate. –Or we can equivalently say the Nyquist sampling rate is ½ the sampling frequency, fs B. Baas, EEC 281 432 Upsampling Upsampling or Interpolation •For an upsampling by a factor of I, add I‐1 zeros between samples in the original sequence •An upsampling by a factor I is commonly written I For example, upsampling by two: 2 • Obviously the number of samples will approximately double after 2 •Note that if the sampling frequency doubles after an upsampling by two, that t the original sample sequence will occur at the same points in time t B. Baas, EEC 281 434 Original Signal Spectrum •Example signal with most energy near DC •Notice 5 spectral “bumps” between large signal “bumps” B. Baas, EEC 281 π 2π435 Upsampled Signal (Time) •One zero is inserted between the original samples for 2x upsampling B. Baas, EEC 281 436 Upsampled Signal Spectrum (Frequency) • Spectrum of 2x upsampled signal •Notice the location of the (now somewhat compressed) five “bumps” on each side of π B. -

Discrete Generalizations of the Nyquist-Shannon Sampling Theorem
DISCRETE SAMPLING: DISCRETE GENERALIZATIONS OF THE NYQUIST-SHANNON SAMPLING THEOREM A DISSERTATION SUBMITTED TO THE DEPARTMENT OF ELECTRICAL ENGINEERING AND THE COMMITTEE ON GRADUATE STUDIES OF STANFORD UNIVERSITY IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY William Wu June 2010 © 2010 by William David Wu. All Rights Reserved. Re-distributed by Stanford University under license with the author. This work is licensed under a Creative Commons Attribution- Noncommercial 3.0 United States License. http://creativecommons.org/licenses/by-nc/3.0/us/ This dissertation is online at: http://purl.stanford.edu/rj968hd9244 ii I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. Brad Osgood, Primary Adviser I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. Thomas Cover I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. John Gill, III Approved for the Stanford University Committee on Graduate Studies. Patricia J. Gumport, Vice Provost Graduate Education This signature page was generated electronically upon submission of this dissertation in electronic format. An original signed hard copy of the signature page is on file in University Archives. iii Abstract 80, 0< 11 17 æ 80, 1< 5 81, 0< 81, 1< 12 83, 1< 84, 0< 82, 1< 83, 4< 82, 3< 15 7 6 83, 2< 83, 3< 84, 8< 83, 6< 83, 7< 13 3 æ æ æ æ æ æ æ æ æ æ 9 -5 -4 -3 -2 -1 1 2 3 4 5 84, 4< 84, 13< 84, 14< 1 HIS DISSERTATION lays a foundation for the theory of reconstructing signals from T finite-dimensional vector spaces using a minimal number of samples. -

Lecture 8B Upsampling Arbitrary Resampling
EE123 Digital Signal Processing Lecture 8B Upsampling Arbitrary Resampling M. Lustig, EECS UC Berkeley Changing Sampling-rate via D.T Processing j! 1 j(w/M 2⇡i/M) X (e )= X e − d M i=0 X ⇣ ⌘ X ⇡ ⇡ − M=2 Xd ... ⇡ ⇡ − Scale by M=2 Shift by (i=1)*2π/(M=2) M. Lustig, EECS UC Berkeley Changing Sampling-rate via D.T Processing j! 1 j(w/M 2⇡i/M) X (e )= X e − d M i=0 X ⇣ ⌘ X ⇡ ⇡ − M=3 Xd ⇡ ⇡ − Scale by M=3 Shift by (i=1)*2π/(M=3) Shift by (i=2)*2π/(M=3) M. Lustig, EECS UC Berkeley Changing Sampling-rate via D.T Processing j! 1 j(w/M 2⇡i/M) X (e )= X e − d M i=0 X ⇣ ⌘ X ⇡ ⇡ − M=3 Xd ... ⇡ ⇡ − M. Lustig, EECS UC Berkeley Anti-Aliasing LPF x[n] ↓M ⇡/M x˜[n] x˜d[n] =˜x[nM] X ⇡ ⇡ − M=3 Xd ⇡ ⇡ − M. Lustig, EECS UC Berkeley UpSampling • Much like D/C converter • Upsample by A LOT ⇒ almost continuous • Intuition: – Recall our D/C model: x[n] ⇒ xs(t)⇒xc(t) – Approximate “xs(t)” by placing zeros between samples – Convolve with a sinc to obtain “xc(t)” M. Lustig, EECS UC Berkeley Up-sampling x[n]=xc(nT ) T xi[n]=xc(nT 0) where T 0 = L integer L Obtain xi[n] from x[n] in two steps: x[n/L] n =0, L, 2L, (1) Generate: x = e 0 otherwise± ± ··· ⇢ x[n] xe[n] M. Lustig, EECS UC Berkeley Up-Sampling (2) Obtain xi[n] from xe[n] by bandlimited interpolation: n xe[0] sinc xe[n] · L ⇣ ⌘ .. -

The Discrete Fourier Transform
Chapter 5 The Discrete Fourier Transform Contents Overview . 5.3 Definition(s) . 5.4 Frequency domain sampling: Properties and applications . 5.9 Time-limited signals . 5.12 The discrete Fourier transform (DFT) . 5.12 The DFT, IDFT - computational perspective . 5.14 Properties of the DFT, IDFT . 5.15 Multiplication of two DFTs and circular convolution . 5.19 Related DFT properties . 5.23 Linear filtering methods based on the DFT . 5.24 Filtering of long data sequences . 5.25 Frequency analysis of signals using the DFT . 5.27 Interpolation / upsampling revisited . 5.29 Summary . 5.31 DFT-based “real-time” filtering . 5.31 5.1 5.2 c J. Fessler, May 27, 2004, 13:14 (student version) x[n] = xa(nTs) Sum of shifted replicates Sampling xa(t) x[n] xps[n] Bandlimited: Time-limited: Sinc interpolation Rectangular window FT DTFT DFT DTFS Sum shifted scaled replicates X[k] = (!) != 2π k X j N Sampling X (F ) (!) X[k] a X Bandlimited: Time-limited: PSfrag replacements Rectangular window Dirichlet interpolation The FT Family Relationships FT Unit Circle • X (F ) = 1 x (t) e−|2πF t dt • a −∞ a x (t) = 1 X (F ) e|2πF t dF • a −∞R a DTFT • R 1 −|!n (!) = n=−∞ x[n] e = X(z) z=ej! • X π j Z x[n] = 1 (!) e|!n d! • 2πP −π X Sample Unit Circle Uniform Time-Domain Sampling X(z) • x[n] = x (RnT ) • a s (!) = 1 1 X !=(2π)−k (sum of shifted scaled replicates of X ( )) • X Ts k=−∞ a Ts a · Recovering xa(t) from x[n] for bandlimited xa(t), where Xa(F ) = 0 for F Fs=2 • P j j ≥ X (F ) = T rect F (2πF T ) (rectangular window to pick out center replicate) • a s Fs X s x (t) = 1 x[n] sinc t−nTs ; where sinc(x) = sin(πx) =(πx). -

Lecture 8 Introduction to Multirate
MUS420 / EE367A Winter ’00 Lecture 8 Introduction to Multirate Topics for Today • Upsampling and Downsampling • Multirate Identities • Polyphase • Decimation and Interpolation • Fractional Delay • Sampling Rate Conversion • Multirate Analysis of STFT Filterbank Main References (please see website for full citations). • Vaidyanathan, Ch.4,11 • Vetterli Ch. 3 • Laakso, et al. “Splitting the Unit Delay” (see 421 citations) • http://www-ccrma.stanford.edu/~jos/resample/ 1 Z transform For this lecture, we do frequency-domain analysis more generally using the z-transform: ∞ ∆ −n X(z) = X x[n]z ; z ∈ ROC(x) n=−∞ To obtain the DTFT, evaluate at z = ejω. Signal Notation We refer interchangeably to “x[n]” as the signal x evaluated at time n, or as the entire signal vector. Please excuse this lapse in rigor, as otherwise simple operations such as modulation (e.g. w[n] = x[n]y[n]) become cumbersome. 2 Upsampling and Downsampling Upsampling • Notation: xM y • Basic Idea: To upsample by integer M, stuff M − 1 zeros in between the samples of x[n]. • Time Domain x[n/M], M divides N y[n] = 0 otherwise. • Frequency Domain Y (z) = X(zM ) • Plugging in z = ejω, we see that the spectrum in [−π,π) contracts by factor M and M images placed around the unit circle: −π π −π π 3 Downsampling • Notation: xN y • Basic Idea: Take every N th sample. • Time Domain: y[n] = x[Nn] • Frequency Domain: N−1 1 j2πk/N 1/N Y (z) = X X(e z ) N k=0 1/Ν −π π −π π Proof: Upsampling establishes a one-to-one correspondence between • S1, the space of all discrete-time signals, and • SN , space of signals nonzero only at integer multiples kN. -

EECS 20N: Structure and Interpretation of Signals And
EECS 20N: Structure and Interpretation of Signals and Systems Final Exam Department of Electrical Engineering and Computer Sciences 13 December 2005 UNIVERSITY OF CALIFORNIA BERKELEY LAST Name FIRST Name Lab Time ² (10 Points) Please print your name and lab time in legible, block lettering above, and on the back of the last page. ² This exam should take you about two hours to complete. However, you will be given up to about three hours to work on it. We recommend that you budget your time as a function of the point allocation and difficulty level (for you) of each problem or modular portion thereof. ² This exam printout consists of pages numbered 1 through 14. Also in- cluded is a double-sided appendix sheet containing transform properties. When you are prompted by the teaching staff to begin work, verify that your copy of the exam is free of printing anomalies and contains all of the fourteen numbered pages and the appendix. If you find a defect in your copy, notify the staff immediately. ² This exam is closed book. Collaboration is not permitted. You may not use or access, or cause to be used or accessed, any reference in print or elec- tronic form at any time during the quiz. Computing, communication, and other electronic devices (except dedicated timekeepers) must be turned off. Noncompliance with these or other instructions from the teaching staff— including, for example, commencing work prematurely or continuing beyond the announced stop time—is a serious violation of the Code of Student Conduct. ² Please write neatly and legibly, because if we can’t read it, we can’t grade it. -

Theory of Upsampled Digital Audio
Theory of Upsampled Digital Audio Doug Rife, DRA Labs Revised May 28, 2002 Introduction This paper is a detailed exposition of the ideas on this subject first published as a brief Letter to the Editor in the December 2000 issue of Stereophile Magazine. In the last few years, several DACs have appeared on the market and sold as “upsampling” DACs. Upsampling DAC manufacturers claim that their products improve the sound quality of standard CDs as compared to conventional DACs and most listeners agree. What can possibility account for the improved sound quality? After all, the digital data on the CD is the same no matter what DAC is used to convert it to analog form. The most popular theory to explain the superior sound quality of upsampling DACs is the time smearing theory. As will be explained shortly, all upsampling DACs employ slow roll-off digital reconstruction filters as opposed to conventional DACs, which employ sharp roll-off or brick wall reconstruction filters. Since slow roll-off filters show less time smear than brick wall filters when measured using artificial digital test signals, many have concluded that reduced time smearing is responsible for the subjective improvement in sound quality when playing CDs through upsampling DACs. Although this seems logical and is an appealing explanation, as will be shown, it falls apart upon closer examination. The main reason is that the digital audio data residing on a CD is already irreparably time smeared. No amount post- processing of the digital audio data by the playback system can possibility remove or reduce this time smearing.