DOCSLIB.ORG

ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform Department of Electrical Engineering University of Arkansas ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform Dr. Jingxian Wu [email protected] 2 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • DTFT of Sampled Signals • Upsampling and downsampling 3 DTFT • Discrete-time Fourier Transform (DTFT) X () x(n)e jn n – (radians): digital frequency • Review: Z-transform: X (z) x(n)zn n0 j X () X (z) | j – Replace z with e . ze • Review: Fourier transform: X () x(t)e jt – (rads/sec): analog frequency 4 DTFT • Relationship between DTFT and Fourier Transform – Sample a continuous time signal x a ( t ) with a sampling period T xs (t) xa (t) (t nT ) xa (nT ) (t nT ) n n – The Fourier Transform of ys (t) jt jnT X s () xs (t)e dt xa (nT)e n – Define: T • : digital frequency (unit: radians) • : analog frequency (unit: radians/sec) – Let x(n) xa (nT) X () X s T 5 DTFT • Relationship between DTFT and Fourier Transform (Cont’d) – The DTFT can be considered as the scaled version of the Fourier transform of the sampled continuous-time signal jt jnT X s () xs (t)e dt xa (nT)e n x(n) x (nT) T a jn X () X s x(n)e T n 6 DTFT • Discrete Frequency – Unit: radians (the unit of continuous frequency is radians/sec) – X ( ) is a periodic function with period 2 j2 n jn j2n jn X ( 2 ) x(n)e x(n)e e x(n)e X () n n n – We only need to consider for • For Fourier transform, we need to consider 1 – f T 2 2T 1 – f T 2 2T 7 DTFT • Example: find the DTFT of the following signal – 1. x(n) (n) n – 2. x(n) u(n), 1 8 DTFT • Example – Find the DTFT of x(n) u(n) u(n N) 9 DTFT • Example – Find the DTFT of the following signal x(n) |n|, 1 • Existence of DTFT – The DTFT of x(n) exists if x(n) satisfies | x(n) | n 10 DTFT • Inverse DTFT 1 jn x(n) X ()e d 2 2 • Example – Find the inverse DTFT of ( 0 ) 11 DTFT • Example – Find the DTFT of cos(0n ) 12 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • DTFT of Sampled Signals • Upsampling and downsampling 13 PROPERTIES • Periodicity X ( 2) X() • Linearity x (n) X () – If x1(n) X1() 2 2 – Then x1(n) x2(n) X1() X2 () 14 PROPERTIES • Time shifting – If x(n) X () – Then jn0 x(n n0 ) X ()e • Frequency shifting – If x(n) X () – Then j0n e x(n) X ( 0 ) 15 PROPERTIES • Differentiation in Frequency – If x(n) X () – Then dX () nx(n) j d d nx(n) z X (z) – Review dz • Example n – Find the DTFT of n u(n) | |1 16 PROPERTIES • Convolution – If y(n) h(n) x(n) – Then Y() H()X () • Example – Find the frequency response of the system y(n) x(n n0 ) 17 PROPERTIES • Example n 1 – A LTI system with impulse response h(n) u(n) n 2 if the input is 1 x(n) u(n) 3 Find the output 18 PROPERTIES • Example – The frequency response of an ideal low pass filter is 1, 0 c H() 0, c find the impulse response. (1) Assume c 0 . 5 . If the sampling rate of the input signal is 1 KHz, what is the cutoff frequency for the analog signal? (2) If the sampling rate of the input signal is 2 KHz, what is the cutoff frequency of the analog signal? 19 PROPERTIES • Modulation – If y(n) x1(n)x2 (n) – Then 1 2 Y() X1( p)X 2 ( p)dp 2 0 20 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • Application: DTFT of Sampled Signals • Upsampling and downsampling 21 APPLICATION: SAMPLING THEOREM • Sampling theorem: time domain – Sampling: convert the continuous-time signal to discrete-time signal. xa (t) p(t) (t nT ) n sampling period xs (t) xa (t)p(t) 22 APPLICATION: SAMPLING THEOREM • Sampling theorem: frequency domain – Fourier transform of the impulse train • impulse train is periodic Fourier series 1 p(t) (t nT ) 1 e jnst 2 s n T n T • Find Fourier transform on both sides 2 P() ( ns ) T n • Time domain multiplication Frequency domain convolution 1 x(t) p(t) X () P() 2 a 1 2 xs (t) x(t) p(t) X s () X a n T n T 23 APPLICATION: SAMPLING THEOREM • Sampling theorem: frequency domain – Sampling in time domain Repetition in frequency domain 24 APPLICATION: SAMPLING THEOREM • Sampling theorem – If the sampling rate is twice of the bandwidth, then the original signal can be perfectly reconstructed from the samples. s 2B s 2B s 2B s 2B aliasing Department of Engineering Science Sonoma State University 25 APPLICATION: SAMPLING THEOREM • Analog signal x a ( t ) v.s. sampled signal x s ( t ) v.s. discrete-time x(n) signal x(n) xa (nT ) Discrete-time signal Samples of continuous-time signal x (t) (t nT ) x (nT ) (t nT ) x(n) (t nT ) xs ( t) a a n n n xs (t) x(n) (t nT ) n 26 APPLICATION: SAMPLING THEOREM • Fourier transform of sampled signal jt jnT X s () xs (t)e dt x(n)e n • DTFT of discrete-time signal X () x(n)e jn n • Relationship X () X s T DTFT of discrete-time signal Fourier transform of continuous-time signal 27 APPLICATION: SAMPLING THEOREM • Relationship among X (), X s (), X a () – X () X s T 1 2 X s () X a n T n T 1 2 X () X a n T n T T T 28 APPLICATION: SAMPLING THEOREM • Example – Consider the analog signal x a ( t ) with Fourier transform shown in the figure. The signal has a one-sided bandwidth 5 Hz. The signal is sampled with a sampling period T . 25ms X () Draw X s ( ) and 1 29 APPLICATION: SAMPLING THEOREM • Reconstruction of sampled signal – If there is no aliasing during sampling, the analog signal can be reconstructed by passing the sampled signal through an ideal low pass filter with cutoff frequency B T, | | s H() 2 0, otherwise t h(t) sin c T xs (t) x(n) (t nT ) n t nT xˆa (t) xs (t) h(t) x(n)sinc n T 30 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • Application: DTFT of Sampled Signals • Upsampling and downsampling 31 UPSAMPLING AND DOWNSAMPLING • Sampling rate conversion – In many applications, we may have to change the sampling rate of a signal as the signal undergoes successive stage of processing. • E.g. Rate h1(n) h2 (n) conversion h3(n) T Sampling period T1 T1 2 – If h ( n ) is a low pass filter with the cut-off frequency being 2 0 u then what is the largest value of T 2 ? 32 UPSAMPLING AND DOWNSAMPLING • Sampling rate conversion – Sampling rate conversion can be directly performed in the digital domain – Downsampling (decimation) • Reduce the sampling frequency (less samples per unit time) – Upsampling (interpolation) • Increase the sampling frequency (more samples per unit time) 33 UPSAMPLING AND DOWNSAMPLING • Downsampling (decimation) – Assume a digital signal,x ( n ) , is obtained by sampling an analog signal x a ( t ) at a sampling period T (or a sampling frequency 1/T). x(n) xa (nT ) – The signal can also be sampled with a sampling period MT (or a lower sampling frequency 1/(MT) ) xd (n) xa (nMT) – Relationship between x ( n ) and xd (n) xd (n) x(nM ) – x d ( n ) is the downsampled (or decimated) version of x(n) • can be obtained by picking one sample out of every M consecutive samples of x(n) decimation. x(n) [x(0), x(1), x(2), x(3), x(4), x(5), x(6), x(7), x(8),] x (n) [x(0), x(3), x(6), ,] M 3 d 34 UPSAMPLING AND DOWNSAMPLING • Downsampling (decimation): frequency domain – Assume all the sampling rates are higher than the Nyquist sampling rate – The DTFT of x(n) with a sampling period T 1 X () X a T T – The DTFT of x d ( n ) with a sampling period MT 1 X d () X a MT MT 1 X d () X M M 35 UPSAMPLING AND DOWNSAMPLING • Example – Consider the frequency response of an ideal low pass filter 1, H() 2 2 0, , 2 2 • Determine h(n) • If we downsample h(n) with a factor of M = 2. Find the downsampled response in both the time and frequency domains. 36 UPSAMPLING AND DOWNSAMPLING • Upsampling (interpolation) – Assume a digital signal,x ( n ) , is obtained by sampling an analog signal x a ( t ) at a sampling period T (or a sampling frequency 1/T). x(n) xa (nT ) – Upsampling by a factor of L • Inserting L-1 zeros between the original samples x(n) [x(0), x(1), x(2), x(3),] L 3 xu (n) [x(0),0,0, x(1),0,0, x(2),0,0, x(3),] T – The effective sampling period of the upsampled signal (sampling L rate: L ) T xu (n) xu (kL) x(k) if n / L k is an integer xu (n) 0, if n / L integer 37 UPSAMPLING AND DOWNSAMPLING • Upsampling (interpolation): frequency domain – The DTFT of x u ( n ) with a sampling period T/L jn jkL X u () xu (n)e x(k)e X (L) n k • The DTFT of X ( ) is compressed in the frequency domain 38 UPSAMPLING AND DOWNSAMPLING • Example – A discrete pulse is given by x(n) = u(n)-u(n-4).
Load more

Recommended publications
  • Detection and Estimation Theory Introduction to ECE 531 Mojtaba Soltanalian- UIC the Course
    Detection and Estimation Theory Introduction to ECE 531 Mojtaba Soltanalian- UIC The course Lectures are given Tuesdays and Thursdays, 2:00-3:15pm Office hours: Thursdays 3:45-5:00pm, SEO 1031 Instructor: Prof. Mojtaba Soltanalian office: SEO 1031 email: [email protected] web: http://msol.people.uic.edu/ The course Course webpage: http://msol.people.uic.edu/ECE531 Textbook(s): * Fundamentals of Statistical Signal Processing, Volume 1: Estimation Theory, by Steven M. Kay, Prentice Hall, 1993, and (possibly) * Fundamentals of Statistical Signal Processing, Volume 2: Detection Theory, by Steven M. Kay, Prentice Hall 1998, available in hard copy form at the UIC Bookstore. The course Style: /Graduate Course with Active Participation/ Introduction Let’s start with a radar example! Introduction> Radar Example QUIZ Introduction> Radar Example You can actually explain it in ten seconds! Introduction> Radar Example Applications in Transportation, Defense, Medical Imaging, Life Sciences, Weather Prediction, Tracking & Localization Introduction> Radar Example The strongest signals leaking off our planet are radar transmissions, not television or radio. The most powerful radars, such as the one mounted on the Arecibo telescope (used to study the ionosphere and map asteroids) could be detected with a similarly sized antenna at a distance of nearly 1,000 light-years. - Seth Shostak, SETI Introduction> Estimation Traditionally discussed in STATISTICS. Estimation in Signal Processing: Digital Computers ADC/DAC (Sampling) Signal/Information Processing Introduction> Estimation The primary focus is on obtaining optimal estimation algorithms that may be implemented on a digital computer. We will work on digital signals/datasets which are typically samples of a continuous-time waveform.
    [Show full text]
  • Designing Commutative Cascades of Multidimensional Upsamplers And
    IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 0 Designing Commutative Cascades of Multidimensional Upsamplers and Downsamplers Brian L. Evans, Member, IEEE Abstract In multiple dimensions, the cascade of an upsampler by L and a downsampler by L commutes if and only if the integer matrices L and M are right coprime and LM = ML. This pap er presents algorithms to design L and M that yield commutative upsampler/dowsampler cascades. We prove that commutativity is p ossible if the 1 Jordan canonical form of the rational resampling matrix R = LM is equivalent to the Smith-McMillan form of R. A necessary condition for this equivalence is that R has an eigendecomp osition and the eigenvalues are rational. B. L. Evans is with the Department of Electrical and Computer Engineering, The UniversityofTexas at Austin, Austin, TX 78712-1084, USA. E-mail: [email protected], Web: http://www.ece.utexas.edu/~b evans, Phone: 512 232-1457, Fax: 512 471-5907. This work was sp onsored in part by NSF CAREER Award under Grant MIP-9702707. July 31, 1997 DRAFT IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 1 I. Introduction 1 Resampling systems scale the sampling rate by a rational factor R = L=M = LM , or 1 equivalently decimate by H = M=L = L M [1], by essentially upsampling by L, ltering, and downsampling by M . In converting compact disc data sampled at 44.1 kHz to digital audio tap e 48000 Hz 160 data sampled at 48 kHz, R = = . Because we can always factor R into coprime 44100 Hz 147 integers L and M , we can always commute the upsampler and downsampler which leads to ecient p olyphase structures of the resampling system.
    [Show full text]
  • Z-Transformation - I
    Digital signal processing: Lecture 5 z-transformation - I Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/1 Review of last lecture • Fourier transform & inverse Fourier transform: – Time domain & Frequency domain representations • Understand the “true face” (latent factor) of some physical phenomenon. – Key points: • Definition of Fourier transformation. • Definition of inverse Fourier transformation. • Condition for a signal to have FT. Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/2 Review of last lecture • The sampling theorem – If the highest frequency component contained in an analog signal is f0, the sampling frequency (the Nyquist rate) should be 2xf0 at least. • Frequency response of an LTI system: – The Fourier transformation of the impulse response – Physical meaning: frequency components to keep (~1) and those to remove (~0). – Theoretic foundation: Convolution theorem. Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/3 Topics of this lecture Chapter 6 of the textbook • The z-transformation. • z－変換 • Convergence region of z- • z－変換の収束領域 transform. －変換とフーリエ変換 • Relation between z- • z transform and Fourier • z－変換と差分方程式 transform. • 伝達関数 or システム • Relation between z- 関数 transform and difference equation. • Transfer function (system function). Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/4 z-transformation（z-変換） • Laplace transformation is important for analyzing analog signal/systems. • z-transformation is important for analyzing discrete signal/systems. • For a given signal x(n), its z-transformation is defined by ∞ Z[x(n)] = X (z) = ∑ x(n)z−n (6.3) n=0 where z is a complex variable. Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/5 One-sided z-transform and two-sided z-transform • The z-transform defined above is called one- sided z-transform (片側ｚ-変換）.
    [Show full text]
  • Basics on Digital Signal Processing
    Basics on Digital Signal Processing z - transform - Digital Filters Vassilis Anastassopoulos Electronics Laboratory, Physics Department, University of Patras Outline of the Lecture 1. The z-transform 2. Properties 3. Examples 4. Digital filters 5. Design of IIR and FIR filters 6. Linear phase 2/31 z-Transform 2 N 1 N 1 j nk n X (k) x(n) e N X (z) x(n) z n0 n0 Time to frequency Time to z-domain (complex) Transformation tool is the Transformation tool is complex wave z e j e j j j2k / N e e With amplitude ρ changing(?) with time With amplitude |ejω|=1 The z-transform is more general than the DFT 3/31 z-Transform For z=ejω i.e. ρ=1 we work on the N 1 unit circle X (z) x(n) z n And the z-transform degenerates n0 into the Fourier transform. I -z z=R+jI |z|=1 R The DFT is an expression of the z-transform on the unit circle. The quantity X(z) must exist with finite value on the unit circle i.e. must posses spectrum with which we can describe a signal or a system. 4/31 z-Transform convergence We are interested in those values of z for which X(z) converges. This region should contain the unit circle. I Why is it so? |a| N 1 N 1 X (z) x(n) zn x(n) (1/zn ) n0 n0 R At z=0, X(z) diverges ROC The values of z for which X(z) diverges are called poles of X(z).
    [Show full text]
  • 3F3 – Digital Signal Processing (DSP)
    3F3 – Digital Signal Processing (DSP) Simon Godsill www-sigproc.eng.cam.ac.uk/~sjg/teaching/3F3 Course Overview • 11 Lectures • Topics: – Digital Signal Processing – DFT, FFT – Digital Filters – Filter Design – Filter Implementation – Random signals – Optimal Filtering – Signal Modelling • Books: – J.G. Proakis and D.G. Manolakis, Digital Signal Processing 3rd edition, Prentice-Hall. – Statistical digital signal processing and modeling -Monson H. Hayes –Wiley • Some material adapted from courses by Dr. Malcolm Macleod, Prof. Peter Rayner and Dr. Arnaud Doucet Digital Signal Processing - Introduction • Digital signal processing (DSP) is the generic term for techniques such as filtering or spectrum analysis applied to digitally sampled signals. • Recall from 1B Signal and Data Analysis that the procedure is as shown below: • is the sampling period • is the sampling frequency • Recall also that low-pass anti-aliasing filters must be applied before A/D and D/A conversion in order to remove distortion from frequency components higher than Hz (see later for revision of this). • Digital signals are signals which are sampled in time (“discrete time”) and quantised. • Mathematical analysis of inherently digital signals (e.g. sunspot data, tide data) was developed by Gauss (1800), Schuster (1896) and many others since. • Electronic digital signal processing (DSP) was first extensively applied in geophysics (for oil-exploration) then military applications, and is now fundamental to communications, mobile devices, broadcasting, and most applications of signal and image processing. There are many advantages in carrying out digital rather than analogue processing; among these are flexibility and repeatability. The flexibility stems from the fact that system parameters are simply numbers stored in the processor.
    [Show full text]
  • CONVOLUTION: Digital Signal Processing .R .Hamming, W
    CONVOLUTION: Digital Signal Processing AN-237 National Semiconductor CONVOLUTION: Digital Application Note 237 Signal Processing January 1980 Introduction As digital signal processing continues to emerge as a major Decreasing the pulse width while increasing the pulse discipline in the field of electrical engineering, an even height to allow the area under the pulse to remain constant, greater demand has evolved to understand the basic theo- Figure 1c, shows from eq(1) and eq(2) the bandwidth or retical concepts involved in the development of varied and spectral-frequency content of the pulse to have increased, diverse signal processing systems. The most fundamental Figure 1d. concepts employed are (not necessarily listed in the order Further altering the pulse to that of Figure 1e provides for an [ ] of importance) the sampling theorem 1 , Fourier transforms even broader bandwidth, Figure 1f. If the pulse is finally al- [ ][] 2 3, convolution, covariance, etc. tered to the limit, i.e., the pulsewidth being infinitely narrow The intent of this article will be to address the concept of and its amplitude adjusted to still maintain an area of unity convolution and to present it in an introductory manner under the pulse, it is found in 1g and 1h the unit impulse hopefully easily understood by those entering the field of produces a constant, or ``flat'' spectrum equal to 1 at all digital signal processing. frequencies. Note that if ATe1 (unit area), we get, by defini- It may be appropriate to note that this article is Part II (Part I tion, the unit impulse function in time.
    [Show full text]
  • The Scientist and Engineer's Guide to Digital Signal Processing Properties of Convolution
    CHAPTER 7 Properties of Convolution A linear system's characteristics are completely specified by the system's impulse response, as governed by the mathematics of convolution. This is the basis of many signal processing techniques. For example: Digital filters are created by designing an appropriate impulse response. Enemy aircraft are detected with radar by analyzing a measured impulse response. Echo suppression in long distance telephone calls is accomplished by creating an impulse response that counteracts the impulse response of the reverberation. The list goes on and on. This chapter expands on the properties and usage of convolution in several areas. First, several common impulse responses are discussed. Second, methods are presented for dealing with cascade and parallel combinations of linear systems. Third, the technique of correlation is introduced. Fourth, a nasty problem with convolution is examined, the computation time can be unacceptably long using conventional algorithms and computers. Common Impulse Responses Delta Function The simplest impulse response is nothing more that a delta function, as shown in Fig. 7-1a. That is, an impulse on the input produces an identical impulse on the output. This means that all signals are passed through the system without change. Convolving any signal with a delta function results in exactly the same signal. Mathematically, this is written: EQUATION 7-1 The delta function is the identity for ( ' convolution. Any signal convolved with x[n] *[n] x[n] a delta function is left unchanged. This property makes the delta function the identity for convolution. This is analogous to zero being the identity for addition (a%0 ' a), and one being the identity for multiplication (a×1 ' a).
    [Show full text]
  • Exploring Anti-Aliasing Filters in Signal Conditioners for Mixed-Signal, Multimodal Sensor Conditioning by Arun T
    Texas Instruments Incorporated Amplifiers: Op Amps Exploring anti-aliasing filters in signal conditioners for mixed-signal, multimodal sensor conditioning By Arun T. Vemuri Systems Architect, Enhanced Industrial Introduction Figure 1. Multimodal, mixed-signal sensor-signal conditioner Some sensor-signal conditioners are used to process the output Analog Digital of multiple sense elements. This Domain Domain processing is often provided by multimodal, mixed-signal condi- tioners that can handle the out- puts from several sense elements Sense Digital Amplifier 1 ADC 1 at the same time. This article Element 1 Filter 1 analyzes the operation of anti- Processed aliasing filters in such sensor- Intelligent Output Compensation signal conditioners. Sense Digital Basics of sensor-signal Amplifier 2 ADC 2 Element 2 Filter 2 conditioners Sense elements, or transducers, convert a physical quantity of interest into electrical signals. Examples include piezo resistive bridges used to measure pres- sure, piezoelectric transducers used to detect ultrasonic than one sense element is processed by the same signal waves, and electrochemical cells used to measure gas conditioner is called multimodal signal conditioning. concentrations. The electrical signals produced by sense Mixed-signal signal conditioning elements are small and exhibit nonidealities, such as tem- Another aspect of sensor-signal conditioning is the electri- perature drifts and nonlinear transfer functions. cal domain in which the signal conditioning occurs. TI’s Sensor analog front ends such as the Texas Instruments PGA309 is an example of a device where the signal condi- (TI) LMP91000 and sensor-signal conditioners such as TI’s tioning of resistive-bridge sense elements occurs in the PGA400/450 are used to amplify the small signals produced analog domain.
    [Show full text]
  • Digital Signal Processing: Theory and Practice, Hardware and Software
    AC 2009-959: DIGITAL SIGNAL PROCESSING: THEORY AND PRACTICE, HARDWARE AND SOFTWARE Wei PAN, Idaho State University Wei Pan is Assistant Professor and Director of VLSI Laboratory, Electrical Engineering Department, Idaho State University. She has several years of industrial experience including Siemens (project engineering/management.) Dr. Pan is an active member of ASEE and IEEE and serves on the membership committee of the IEEE Education Society. S. Hossein Mousavinezhad, Idaho State University S. Hossein Mousavinezhad is Professor and Chair, Electrical Engineering Department, Idaho State University. Dr. Mousavinezhad is active in ASEE and IEEE and is an ABET program evaluator. Hossein is the founding general chair of the IEEE International Conferences on Electro Information Technology. Kenyon Hart, Idaho State University Kenyon Hart is Specialist Engineer and Associate Lecturer, Electrical Engineering Department, Idaho State University, Pocatello, Idaho. Page 14.491.1 Page © American Society for Engineering Education, 2009 Digital Signal Processing, Theory/Practice, HW/SW Abstract Digital Signal Processing (DSP) is a course offered by many Electrical and Computer Engineering (ECE) programs. In our school we offer a senior-level, first-year graduate course with both lecture and laboratory sections. Our experience has shown that some students consider the subject matter to be too theoretical, relying heavily on mathematical concepts and abstraction. There are several visible applications of DSP including: cellular communication systems, digital image processing and biomedical signal processing. Authors have incorporated many examples utilizing software packages including MATLAB/MATHCAD in the course and also used classroom demonstrations to help students visualize some difficult (but important) concepts such as digital filters and their design, various signal transformations, convolution, difference equations modeling, signals/systems classifications and power spectral estimation as well as optimal filters.
    [Show full text]
  • Deep Image Prior for Undersampling High-Speed Photoacoustic Microscopy
    Photoacoustics 22 (2021) 100266 Contents lists available at ScienceDirect Photoacoustics journal homepage: www.elsevier.com/locate/pacs Deep image prior for undersampling high-speed photoacoustic microscopy Tri Vu a,*, Anthony DiSpirito III a, Daiwei Li a, Zixuan Wang c, Xiaoyi Zhu a, Maomao Chen a, Laiming Jiang d, Dong Zhang b, Jianwen Luo b, Yu Shrike Zhang c, Qifa Zhou d, Roarke Horstmeyer e, Junjie Yao a a Photoacoustic Imaging Lab, Duke University, Durham, NC, 27708, USA b Department of Biomedical Engineering, Tsinghua University, Beijing, 100084, China c Division of Engineering in Medicine, Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Cambridge, MA, 02139, USA d Department of Biomedical Engineering and USC Roski Eye Institute, University of Southern California, Los Angeles, CA, 90089, USA e Computational Optics Lab, Duke University, Durham, NC, 27708, USA ARTICLE INFO ABSTRACT Keywords: Photoacoustic microscopy (PAM) is an emerging imaging method combining light and sound. However, limited Convolutional neural network by the laser’s repetition rate, state-of-the-art high-speed PAM technology often sacrificesspatial sampling density Deep image prior (i.e., undersampling) for increased imaging speed over a large field-of-view. Deep learning (DL) methods have Deep learning recently been used to improve sparsely sampled PAM images; however, these methods often require time- High-speed imaging consuming pre-training and large training dataset with ground truth. Here, we propose the use of deep image Photoacoustic microscopy Raster scanning prior (DIP) to improve the image quality of undersampled PAM images. Unlike other DL approaches, DIP requires Undersampling neither pre-training nor fully-sampled ground truth, enabling its flexible and fast implementation on various imaging targets.
    [Show full text]
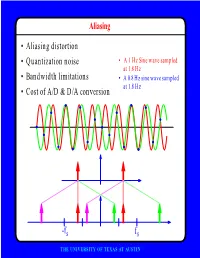
  • F • Aliasing Distortion • Quantization Noise • Bandwidth Limitations • Cost of A/D & D/A Conversion
    Aliasing • Aliasing distortion • Quantization noise • A 1 Hz Sine wave sampled at 1.8 Hz • Bandwidth limitations • A 0.8 Hz sine wave sampled at 1.8 Hz • Cost of A/D & D/A conversion -fs fs THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Perfect reconstruction of a Better trade-off between signal is possible even after bandwidth and noise severe distortion immunity performance digital analog bandwidth Increase signal-to-noise ratio simply by adding more bits SNR = -7.2 + 6 dB/bit THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Programmability • Modifiable in the field • Implement multiple standards • Better user interfaces • Tolerance for changes in specifications • Get better use of hardware for low-speed operations • Debugging • User programmability THE UNIVERSITY OF TEXAS AT AUSTIN Disadvantages of Digital Systems Programmability • Speed is too slow for some applications • High average power and peak power consumption RISC (2 Watts) vs. DSP (50 mW) DATA PROG MEMORY MEMORY HARVARD ARCHITECTURE • Aliasing from undersampling • Clipping from quantization Q[v] v v THE UNIVERSITY OF TEXAS AT AUSTIN Analog-to-Digital Conversion 1 --- T h(t) Q[.] xt() yt() ynT() yˆ()nT Anti-Aliasing Sampler Quantizer Filter xt() y(nT) t n y(t) ^y(nT) t n THE UNIVERSITY OF TEXAS AT AUSTIN Resampling Changing the Sampling Rate • Conversion between audio formats Compact 48.0 Digital Disc ---------- Audio Tape 44.1 KHz44.1 48 KHz • Speech compression Speech 1 Speech for on DAT --- Telephone 48 KHz 6 8 KHz • Video format conversion
    [Show full text]
  • Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform Foundations of Digital Signal Processing
    Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform Foundations of Digital Signal Processing Outline • Review of Sampling • The Nyquist-Shannon Sampling Theorem • Continuous-time Reconstruction / Interpolation • Aliasing and anti-Aliasing • Deriving Transforms from the Fourier Transform • Discrete-time Fourier Transform, Fourier Series, Discrete-time Fourier Series • The Discrete Fourier Transform Foundations of Digital Signal Processing Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform 1 News Homework #5 . Due this week . Submit via canvas Coding Problem #4 . Due this week . Submit via canvas Foundations of Digital Signal Processing Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform 2 Exam 1 Grades The class did exceedingly well . Mean: 89.3 . Median: 91.5 Foundations of Digital Signal Processing Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform 3 Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform Foundations of Digital Signal Processing Outline • Review of Sampling • The Nyquist-Shannon Sampling Theorem • Continuous-time Reconstruction / Interpolation • Aliasing and anti-Aliasing • Deriving Transforms from the Fourier Transform • Discrete-time Fourier Transform, Fourier Series, Discrete-time Fourier Series • The Discrete Fourier Transform Foundations of Digital Signal Processing Lecture 12: Sampling, Aliasing, and the Discrete Fourier Transform 4 Sampling Discrete-Time Fourier Transform Foundations of Digital Signal Processing Lecture 12: Sampling, Aliasing,
    [Show full text]