DOCSLIB.ORG

Discrete Generalizations of the Nyquist-Shannon Sampling Theorem

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Discrete Generalizations of the Nyquist-Shannon Sampling Theorem DISCRETE SAMPLING: DISCRETE GENERALIZATIONS OF THE NYQUIST-SHANNON SAMPLING THEOREM A DISSERTATION SUBMITTED TO THE DEPARTMENT OF ELECTRICAL ENGINEERING AND THE COMMITTEE ON GRADUATE STUDIES OF STANFORD UNIVERSITY IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY William Wu June 2010 © 2010 by William David Wu. All Rights Reserved. Re-distributed by Stanford University under license with the author. This work is licensed under a Creative Commons Attribution- Noncommercial 3.0 United States License. http://creativecommons.org/licenses/by-nc/3.0/us/ This dissertation is online at: http://purl.stanford.edu/rj968hd9244 ii I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. Brad Osgood, Primary Adviser I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. Thomas Cover I certify that I have read this dissertation and that, in my opinion, it is fully adequate in scope and quality as a dissertation for the degree of Doctor of Philosophy. John Gill, III Approved for the Stanford University Committee on Graduate Studies. Patricia J. Gumport, Vice Provost Graduate Education This signature page was generated electronically upon submission of this dissertation in electronic format. An original signed hard copy of the signature page is on file in University Archives. iii Abstract 80, 0< 11 17 æ 80, 1< 5 81, 0< 81, 1< 12 83, 1< 84, 0< 82, 1< 83, 4< 82, 3< 15 7 6 83, 2< 83, 3< 84, 8< 83, 6< 83, 7< 13 3 æ æ æ æ æ æ æ æ æ æ 9 -5 -4 -3 -2 -1 1 2 3 4 5 84, 4< 84, 13< 84, 14< 1 HIS DISSERTATION lays a foundation for the theory of reconstructing signals from T finite-dimensional vector spaces using a minimal number of samples. We call this theory Discrete Sampling. Suppose the signals we wish to reconstruct are drawn from a known k-dimensional subspace of Cn, denoted by Y. Then the two problems that Discrete Sampling seeks to address are: n 1. Interpolating System Problem: Find an index set 2(k) and basis vectors := I ∈ U u : i such that { i ∈ I} f Y : f = f[i]u . ∀ ∈ i i X∈I A pair ( , ) satisfying this equation is called an interpolating system for Y. I U 2. Orthogonal Interpolating System Problem: Find an interpolating system for Y in which the ui’s are orthogonal. iv In the first problem, the pairing of a sampling sequence and a interpolating basis I that can reconstruct all signals in Y is dubbed an interpolating system. These are the U basic objects of interest that we aim to study. The second problem asks for a more refined version of this object, in which the interpolating basis is orthogonal. The Nyquist-Shannon sampling theorem provides an example of an orthogonal interpolating system. There, the 1 1 1 vector space is the Paley-Wiener space Y = − [ , ], the sampling sequence is = Z, F − 2 2 I and the orthogonal basis vectors are = sinc(t i) : i Z . U { − ∈ } In the first half of this dissertation, we provide a simple theoretical framework for iden- tifying and constructing interpolating systems (IS) and orthogonal interpolating systems (OIS) in general finite dimensional vector spaces. This can be thought of as a generaliza- tion of Shannon’s sampling theorem in the finite dimensional setting. Which vector spaces will admit these systems? What algebraic properties must be satisfied? While it can be proven that every vector space has an interpolating system, not all vector spaces have an orthogonal interpolating system. When does an OIS exist, and how can we construct it? In the second half of this dissertation, we investigate interpolating systems in finite- dimensional bandlimited spaces, which are parameterized by their DFT support. We pro- vide algorithms for constructing all orthogonal interpolating systems for such spaces, yield- ing a sampling dictionary. The dictionaries exhibit many patterns, making connections with group theory, number theory, and graph theory, specifically: orbit counting, vanishing sums of roots of unity, primes, modular arithmetic, difference sets, cliques, and perfect graphs. All algorithms described have been implemented and can be run online for further investi- gation at the webMathematica-powered website http://www.discretesampling.com. The remainder of the dissertation deals with smaller topics. We briefly analyze sequency- limited spaces, which are defined by their supports in a Discrete Haar Wavelet Transform domain, and give a classification theorem for all orthogonal interpolating systems in terms of posets and Hasse diagrams. Lastly, we draw connections between our work and coding v theory, and provide thoughts for future research. LINEAR ALGEBRA NUMBER dot products THEORY circulancy projections eigenvalues mod arithmetic COMBINA- coin changing TORICS Vandermonde null space squarefree RREF primality difference sets enumerationnecklacesposets of DISCRETE clique problem SAMPLING perfect graphs adjacency matrix DFT cyclic convolution GRAPH dihedral reproducingwavelets kernel THEORY Polya counting Nyquist-Shannon irreducible poly. vanishing sums of roots of unity HARMONIC ANALYSIS ABSTRACT ALGEBRA vi Acknowledgments ELOW ARE THE MAIN PEOPLE AND ORGANIZATIONS that I would like to thank B for helping me through my graduate school career. Brad Osgood Frank H. and Eva Buck Foundation John Gill Jiehua Chen Thomas Cover Hsin and Frances Wu David Wayne Tillay Ever since my first interaction with him, my principal advisor Brad Osgood has always been extremely supportive, encouraging, and optimistic at all times. Although I initially lacked the maturity to make a dent in the problems he gave me, Brad trained me, and taught me to organize my thoughts in a disciplined fashion. By following his example, keeping meticulous notebooks, and systematically writing to myself in a conversational style, I learned to think about long-term problems in an incremental and patient fashion. In addition, Brad has been extremely generous in sharing his time, his mental energy, and his ideas. I recall once, in hope of deciphering the underlying pattern behind a problem, Brad typed out fifty pages of special cases! Brad also envisioned the foundational theory of Discrete Sampling, inspired by the possibility of sampling more efficiently in medical imaging applications. I must also thank Brad for introducing me to Mathematica, which vii has been crucially helpful for doing research. These lessons in writing, discipline, collabo- ration, and mathematical programming that Brad gave me have deeply changed the way I think. Living up to Brad’s example will be an eternal challenge. I am very appreciative to John Gill for all his support over the years. John gave me guidance both before and after the qualifying exams, and kindly helped me in so many ways, including sharing a lifetime’s worth of research problems, encouraging me to learn Perl, and even recovering data from two broken laptops. I have always been impressed by John’s razor sharp mathematical intuition and computer science know-how, having spent many hours in his office watching him at work. More impressively, John demonstrates how to be both humble and indispensable, and I find that very inspiring. Another personal hero of mine is Thomas Cover, who personifies everything that I once fantasized about becoming as a child – a gambler possessing deep mathematical insights, and also being able to explain them with wit, clarity, style, and tremendous humor. We share a love for clever things. I thank him for helping me get into Stanford, rooting for me during the quals, always offering a haven to share ideas and puzzles on Wednesdays, and for the memorable opportunity to serve as his information theory teaching assistant. I want to thank David Wayne Tillay for inspiring me as a middle school student to pursue math and science. In a town without many opportunities for high academic achieve- ment, “Dr. Tillay” was a shiny anomaly. He gave us sophisticated lab equipment, infused humor into the learning process, and created the only science fair our city ever had. With- out Dr. Tillay, I might have ended up as a starving cartoonist instead of a starving graduate student. I am deeply indebted to the Frank H. and Eva Buck Foundation, which somehow se- lected me as a recipient of its scholarship in 1999, most likely due to an accounting error. My entire tertiary education has been funded through their insane generosity and the stew- ardship of Ms. Gloria Brown. viii I thank a number of researchers in related areas for their consultation and/or giving me public speaking opportunities. Joe Sawada at the University of Guelph was very help- ful in explaining his efficient algorithms for necklace enumeration and identification. Re- searchers who discussed applications with me included Daniel Ensign, Kendall Fruchey, and Daniel Rosenfeld from Stanford’s chemistry department, Daniel M. Spielman from Stanford’s radiological sciences lab, and Babak Hassibi from Caltech’s EE department. Kannan Soundarajan at Stanford lent his expertise in modular arithmetic. I graciously thank Maria Chudnovsky at Columbia University for patiently analyzing the difference graphs with me, and giving me the opportunity to speak in her discrete math seminar. Wal- ter Neumann at Barnard College agreed to an out-of-the-blue discussion with me about cyclotomic polynomials. Sinan Gunturk invited me to give a talk at the Courant Institute, which was very helpful; I also thank Mark Tygert and Ron Peled at the Courant for their insightful discussions. Other academics that invited me to give talks include Julius Smith at CCRMA, Jon Hamkins at JPL, Thierry Klein at Bell Labs, and Amit Singer at Princeton, all providing useful feedback.
Load more

Recommended publications
  • Designing Commutative Cascades of Multidimensional Upsamplers And
    IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 0 Designing Commutative Cascades of Multidimensional Upsamplers and Downsamplers Brian L. Evans, Member, IEEE Abstract In multiple dimensions, the cascade of an upsampler by L and a downsampler by L commutes if and only if the integer matrices L and M are right coprime and LM = ML. This pap er presents algorithms to design L and M that yield commutative upsampler/dowsampler cascades. We prove that commutativity is p ossible if the 1 Jordan canonical form of the rational resampling matrix R = LM is equivalent to the Smith-McMillan form of R. A necessary condition for this equivalence is that R has an eigendecomp osition and the eigenvalues are rational. B. L. Evans is with the Department of Electrical and Computer Engineering, The UniversityofTexas at Austin, Austin, TX 78712-1084, USA. E-mail: [email protected], Web: http://www.ece.utexas.edu/~b evans, Phone: 512 232-1457, Fax: 512 471-5907. This work was sp onsored in part by NSF CAREER Award under Grant MIP-9702707. July 31, 1997 DRAFT IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 1 I. Introduction 1 Resampling systems scale the sampling rate by a rational factor R = L=M = LM , or 1 equivalently decimate by H = M=L = L M [1], by essentially upsampling by L, ltering, and downsampling by M . In converting compact disc data sampled at 44.1 kHz to digital audio tap e 48000 Hz 160 data sampled at 48 kHz, R = = . Because we can always factor R into coprime 44100 Hz 147 integers L and M , we can always commute the upsampler and downsampler which leads to ecient p olyphase structures of the resampling system.
    [Show full text]
  • An Overview of Wavelet Transform Concepts and Applications
    An overview of wavelet transform concepts and applications Christopher Liner, University of Houston February 26, 2010 Abstract The continuous wavelet transform utilizing a complex Morlet analyzing wavelet has a close connection to the Fourier transform and is a powerful analysis tool for decomposing broadband wavefield data. A wide range of seismic wavelet applications have been reported over the last three decades, and the free Seismic Unix processing system now contains a code (succwt) based on the work reported here. Introduction The continuous wavelet transform (CWT) is one method of investigating the time-frequency details of data whose spectral content varies with time (non-stationary time series). Moti- vation for the CWT can be found in Goupillaud et al. [12], along with a discussion of its relationship to the Fourier and Gabor transforms. As a brief overview, we note that French geophysicist J. Morlet worked with non- stationary time series in the late 1970's to find an alternative to the short-time Fourier transform (STFT). The STFT was known to have poor localization in both time and fre- quency, although it was a first step beyond the standard Fourier transform in the analysis of such data. Morlet's original wavelet transform idea was developed in collaboration with the- oretical physicist A. Grossmann, whose contributions included an exact inversion formula. A series of fundamental papers flowed from this collaboration [16, 12, 13], and connections were soon recognized between Morlet's wavelet transform and earlier methods, including harmonic analysis, scale-space representations, and conjugated quadrature filters. For fur- ther details, the interested reader is referred to Daubechies' [7] account of the early history of the wavelet transform.
    [Show full text]
  • A Low Bit Rate Audio Codec Using Wavelet Transform
    Navpreet Singh, Mandeep Kaur,Rajveer Kaur / International Journal of Engineering Research and Applications (IJERA) ISSN: 2248-9622 www.ijera.com Vol. 3, Issue 4, Jul-Aug 2013, pp.2222-2228 An Enhanced Low Bit Rate Audio Codec Using Discrete Wavelet Transform Navpreet Singh1, Mandeep Kaur2, Rajveer Kaur3 1,2(M. tech Students, Department of ECE, Guru kashi University, Talwandi Sabo(BTI.), Punjab, INDIA 3(Asst. Prof. Department of ECE, Guru Kashi University, Talwandi Sabo (BTI.), Punjab,INDIA Abstract Audio coding is the technology to represent information and perceptually irrelevant signal audio in digital form with as few bits as possible components can be separated and later removed. This while maintaining the intelligibility and quality class includes techniques such as subband coding; required for particular application. Interest in audio transform coding, critical band analysis, and masking coding is motivated by the evolution to digital effects. The second class takes advantage of the communications and the requirement to minimize statistical redundancy in audio signal and applies bit rate, and hence conserve bandwidth. There is some form of digital encoding. Examples of this class always a tradeoff between lowering the bit rate and include entropy coding in lossless compression and maintaining the delivered audio quality and scalar/vector quantization in lossy compression [1]. intelligibility. The wavelet transform has proven to Digital audio compression allows the be a valuable tool in many application areas for efficient storage and transmission of audio data. The analysis of nonstationary signals such as image and various audio compression techniques offer different audio signals. In this paper a low bit rate audio levels of complexity, compressed audio quality, and codec algorithm using wavelet transform has been amount of data compression.
    [Show full text]
  • Image Compression Techniques by Using Wavelet Transform
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by International Institute for Science, Technology and Education (IISTE): E-Journals Journal of Information Engineering and Applications www.iiste.org ISSN 2224-5782 (print) ISSN 2225-0506 (online) Vol 2, No.5, 2012 Image Compression Techniques by using Wavelet Transform V. V. Sunil Kumar 1* M. Indra Sena Reddy 2 1. Dept. of CSE, PBR Visvodaya Institute of Tech & Science, Kavali, Nellore (Dt), AP, INDIA 2. School of Computer science & Enginering, RGM College of Engineering & Tech. Nandyal, A.P, India * E-mail of the corresponding author: [email protected] Abstract This paper is concerned with a certain type of compression techniques by using wavelet transforms. Wavelets are used to characterize a complex pattern as a series of simple patterns and coefficients that, when multiplied and summed, reproduce the original pattern. The data compression schemes can be divided into lossless and lossy compression. Lossy compression generally provides much higher compression than lossless compression. Wavelets are a class of functions used to localize a given signal in both space and scaling domains. A MinImage was originally created to test one type of wavelet and the additional functionality was added to Image to support other wavelet types, and the EZW coding algorithm was implemented to achieve better compression. Keywords: Wavelet Transforms, Image Compression, Lossless Compression, Lossy Compression 1. Introduction Digital images are widely used in computer applications. Uncompressed digital images require considerable storage capacity and transmission bandwidth. Efficient image compression solutions are becoming more critical with the recent growth of data intensive, multimedia based web applications.
    [Show full text]
  • JPEG2000: Wavelets in Image Compression
    EE678 WAVELETS APPLICATION ASSIGNMENT 1 JPEG2000: Wavelets In Image Compression Group Members: Qutubuddin Saifee [email protected] 01d07009 Ankur Gupta [email protected] 01d070013 Nishant Singh [email protected] 01d07019 Abstract During the past decade, with the birth of wavelet theory and multiresolution analysis, image processing techniques based on wavelet transform have been extensively studied and tremendously improved. JPEG 2000 uses wavelet transform and provides an integrated toolbox to better address increasing needs for compression. In this report, we study the basic concepts of JPEG2000, the LeGall 5/3 and Daubechies 9/7 wavelets used in it and finally Embedded zerotree wavelet coding and Set Partitioning in Hierarchical Trees. Index Terms Wavelets, JPEG2000, Image Compression, LeGall, Daubechies, EZW, SPIHT. I. INTRODUCTION I NCE the mid 1980s, members from both the International Telecommunications Union (ITU) and the International SOrganization for Standardization (ISO) have been working together to establish a joint international standard for the compression of grayscale and color still images. This effort has been known as JPEG, the Joint Photographic Experts Group. The process was such that, after evaluating a number of coding schemes, the JPEG members selected a discrete cosine transform( DCT)-based method in 1988. From 1988 to 1990, the JPEG group continued its work by simulating, testing and documenting the algorithm. JPEG became Draft International Standard (DIS) in 1991 and International Standard (IS) in 1992. With the continual expansion of multimedia and Internet applications, the needs and requirements of the technologies used grew and evolved. In March 1997, a new call for contributions was launched for the development of a new standard for the compression of still images, the JPEG2000 standard.
    [Show full text]
  • Deep Image Prior for Undersampling High-Speed Photoacoustic Microscopy
    Photoacoustics 22 (2021) 100266 Contents lists available at ScienceDirect Photoacoustics journal homepage: www.elsevier.com/locate/pacs Deep image prior for undersampling high-speed photoacoustic microscopy Tri Vu a,*, Anthony DiSpirito III a, Daiwei Li a, Zixuan Wang c, Xiaoyi Zhu a, Maomao Chen a, Laiming Jiang d, Dong Zhang b, Jianwen Luo b, Yu Shrike Zhang c, Qifa Zhou d, Roarke Horstmeyer e, Junjie Yao a a Photoacoustic Imaging Lab, Duke University, Durham, NC, 27708, USA b Department of Biomedical Engineering, Tsinghua University, Beijing, 100084, China c Division of Engineering in Medicine, Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Cambridge, MA, 02139, USA d Department of Biomedical Engineering and USC Roski Eye Institute, University of Southern California, Los Angeles, CA, 90089, USA e Computational Optics Lab, Duke University, Durham, NC, 27708, USA ARTICLE INFO ABSTRACT Keywords: Photoacoustic microscopy (PAM) is an emerging imaging method combining light and sound. However, limited Convolutional neural network by the laser’s repetition rate, state-of-the-art high-speed PAM technology often sacrificesspatial sampling density Deep image prior (i.e., undersampling) for increased imaging speed over a large field-of-view. Deep learning (DL) methods have Deep learning recently been used to improve sparsely sampled PAM images; however, these methods often require time- High-speed imaging consuming pre-training and large training dataset with ground truth. Here, we propose the use of deep image Photoacoustic microscopy Raster scanning prior (DIP) to improve the image quality of undersampled PAM images. Unlike other DL approaches, DIP requires Undersampling neither pre-training nor fully-sampled ground truth, enabling its flexible and fast implementation on various imaging targets.
    [Show full text]
  • ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform
    Department of Electrical Engineering University of Arkansas ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform Dr. Jingxian Wu [email protected] 2 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • DTFT of Sampled Signals • Upsampling and downsampling 3 DTFT • Discrete-time Fourier Transform (DTFT) X () x(n)e jn n – (radians): digital frequency • Review: Z-transform: X (z) x(n)zn n0 j X () X (z) | j – Replace z with e . ze • Review: Fourier transform: X () x(t)e jt – (rads/sec): analog frequency 4 DTFT • Relationship between DTFT and Fourier Transform – Sample a continuous time signal x a ( t ) with a sampling period T xs (t) xa (t) (t nT ) xa (nT ) (t nT ) n n – The Fourier Transform of ys (t) jt jnT X s () xs (t)e dt xa (nT)e n – Define: T • : digital frequency (unit: radians) • : analog frequency (unit: radians/sec) – Let x(n) xa (nT) X () X s T 5 DTFT • Relationship between DTFT and Fourier Transform (Cont’d) – The DTFT can be considered as the scaled version of the Fourier transform of the sampled continuous-time signal jt jnT X s () xs (t)e dt xa (nT)e n x(n) x (nT) T a jn X () X s x(n)e T n 6 DTFT • Discrete Frequency – Unit: radians (the unit of continuous frequency is radians/sec) – X ( ) is a periodic function with period 2 j2 n jn j2n jn X ( 2 ) x(n)e x(n)e e x(n)e X () n n n – We only need to consider for • For Fourier transform, we need to consider 1 – f T 2 2T 1 – f T 2 2T 7 DTFT • Example: find the DTFT of the following signal – 1.
    [Show full text]
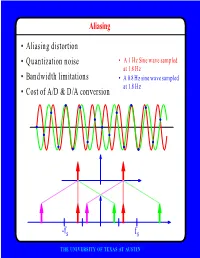
  • F • Aliasing Distortion • Quantization Noise • Bandwidth Limitations • Cost of A/D & D/A Conversion
    Aliasing • Aliasing distortion • Quantization noise • A 1 Hz Sine wave sampled at 1.8 Hz • Bandwidth limitations • A 0.8 Hz sine wave sampled at 1.8 Hz • Cost of A/D & D/A conversion -fs fs THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Perfect reconstruction of a Better trade-off between signal is possible even after bandwidth and noise severe distortion immunity performance digital analog bandwidth Increase signal-to-noise ratio simply by adding more bits SNR = -7.2 + 6 dB/bit THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Programmability • Modifiable in the field • Implement multiple standards • Better user interfaces • Tolerance for changes in specifications • Get better use of hardware for low-speed operations • Debugging • User programmability THE UNIVERSITY OF TEXAS AT AUSTIN Disadvantages of Digital Systems Programmability • Speed is too slow for some applications • High average power and peak power consumption RISC (2 Watts) vs. DSP (50 mW) DATA PROG MEMORY MEMORY HARVARD ARCHITECTURE • Aliasing from undersampling • Clipping from quantization Q[v] v v THE UNIVERSITY OF TEXAS AT AUSTIN Analog-to-Digital Conversion 1 --- T h(t) Q[.] xt() yt() ynT() yˆ()nT Anti-Aliasing Sampler Quantizer Filter xt() y(nT) t n y(t) ^y(nT) t n THE UNIVERSITY OF TEXAS AT AUSTIN Resampling Changing the Sampling Rate • Conversion between audio formats Compact 48.0 Digital Disc ---------- Audio Tape 44.1 KHz44.1 48 KHz • Speech compression Speech 1 Speech for on DAT --- Telephone 48 KHz 6 8 KHz • Video format conversion
    [Show full text]
  • Comparison of Image Compressions: Analog Transformations P
    Proceedings Comparison of Image Compressions: Analog † Transformations P Jose Balsa P CITIC Research Center, Universidade da Coruña (University of A Coruña), 15071 A Coruña, Spain; [email protected] † Presented at the 3rd XoveTIC Conference, A Coruña, Spain, 8–9 October 2020. Published: 21 August 2020 Abstract: A comparison between the four most used transforms, the discrete Fourier transform (DFT), discrete cosine transform (DCT), the Walsh–Hadamard transform (WHT) and the Haar- wavelet transform (DWT), for the transmission of analog images, varying their compression and comparing their quality, is presented. Additionally, performance tests are done for different levels of white Gaussian additive noise. Keywords: analog image transformation; analog image compression; analog image quality 1. Introduction Digitized image coding systems employ reversible mathematical transformations. These transformations change values and function domains in order to rearrange information in a way that condenses information important to human vision [1]. In the new domain, it is possible to filter out relevant information and discard information that is irrelevant or of lesser importance for image quality [2]. Both digital and analog systems use the same transformations in source coding. Some examples of digital systems that employ these transformations are JPEG, M-JPEG, JPEG2000, MPEG- 1, 2, 3 and 4, DV and HDV, among others. Although digital systems after transformation and filtering make use of digital lossless compression techniques, such as Huffman. In this work, we aim to make a comparison of the most commonly used transformations in state- of-the-art image compression systems. Typically, the transformations used to compress analog images work either on the entire image or on regions of the image.
    [Show full text]
  • Wavelet Transform for JPG, BMP & TIFF
    Wavelet Transform for JPG, BMP & TIFF Samir H. Abdul-Jauwad Mansour I. AlJaroudi Electrical Engineering Department, Electrical Engineering Department, King Fahd University of Petroleum & King Fahd University of Petroleum & Minerals Minerals Dhahran 31261, Saudi Arabia Dhahran 31261, Saudi Arabia ABSTRACT This paper presents briefly both wavelet transform and inverse wavelet transform for three different images format; JPG, BMP and TIFF. After brief historical view of wavelet, an introduction will define wavelets transform. By narrowing the scope, it emphasizes the discrete wavelet transform (DWT). A practical example of DWT is shown, by choosing three images and applying MATLAB code for 1st level and 2nd level wavelet decomposition then getting the inverse wavelet transform for the three images. KEYWORDS: Wavelet Transform, JPG, BMP, TIFF, MATLAB. __________________________________________________________________ Correspondence: Dr. Samir H. Abdul-Jauwad, Electrical Engineering Department, King Fahd University of Petroleum & Mineral, Dhahran 1261, Saudi Arabia. Email: [email protected] Phone: +96638602500 Fax: +9663860245 INTRODUCTION In 1807, theories of frequency analysis by Joseph Fourier were the main lead to wavelet. However, wavelet was first appeared in an appendix to the thesis of A. Haar in 1909 [1]. Compact support was one property of the Haar wavelet which means that it vanishes outside of a finite interval. Unfortunately, Haar wavelets have some limits, because they are not continuously differentiable. In 1930, work done separately by scientists for representing the functions by using scale-varying basis functions was the key to understanding wavelets. In 1980, Grossman and Morlet, a physicist and an engineer, provided a way of thinking for wavelets based on physical intuition through defining wavelets in the context of quantum physics [3].
    [Show full text]
  • The Wavelet Tutorial Second Edition Part I by Robi Polikar
    THE WAVELET TUTORIAL SECOND EDITION PART I BY ROBI POLIKAR FUNDAMENTAL CONCEPTS & AN OVERVIEW OF THE WAVELET THEORY Welcome to this introductory tutorial on wavelet transforms. The wavelet transform is a relatively new concept (about 10 years old), but yet there are quite a few articles and books written on them. However, most of these books and articles are written by math people, for the other math people; still most of the math people don't know what the other math people are 1 talking about (a math professor of mine made this confession). In other words, majority of the literature available on wavelet transforms are of little help, if any, to those who are new to this subject (this is my personal opinion). When I first started working on wavelet transforms I have struggled for many hours and days to figure out what was going on in this mysterious world of wavelet transforms, due to the lack of introductory level text(s) in this subject. Therefore, I have decided to write this tutorial for the ones who are new to the topic. I consider myself quite new to the subject too, and I have to confess that I have not figured out all the theoretical details yet. However, as far as the engineering applications are concerned, I think all the theoretical details are not necessarily necessary (!). In this tutorial I will try to give basic principles underlying the wavelet theory. The proofs of the theorems and related equations will not be given in this tutorial due to the simple assumption that the intended readers of this tutorial do not need them at this time.
    [Show full text]
  • JASON Manual
    Weiss Engineering Ltd. Florastrasse 42, 8610 Uster, Switzerland www.weiss-highend.com JASON OWNERS MANUAL OWNERS MANUAL FOR WEISS JASON CD TRANSPORT INTRODUCTION Dear Customer Congratulations on your purchase of the JASON CD Transport and welcome to the family of Weiss equipment owners! The JASON is the result of an intensive research and development process. Research was conducted both in analog and digital circuit design, as well as in signal processing algorithm specification. On the following pages I will introduce you to our views on high quality audio processing. These include fundamental digital and analog audio concepts and the JASON CD Transport. I wish you a long-lasting relationship with your JASON. Yours sincerely, Daniel Weiss President, Weiss Engineering Ltd. Page: 2 Date: 03/13 /dw OWNERS MANUAL FOR WEISS JASON CD TRANSPORT TABLE OF CONTENTS 4 A short history of Weiss Engineering 5 Our mission and product philosophy 6 Advanced digital and analog audio concepts explained 6 Jitter Suppression, Clocking 8 Upsampling, Oversampling and Sampling Rate Conversion in General 11 Reconstruction Filters 12 Analog Output Stages 12 Dithering 14 The JASON CD Transport 14 Features 17 Operation 21 Technical Data 22 Contact Page: 3 Date: 03/13 /dw OWNERS MANUAL FOR WEISS JASON CD TRANSPORT A SHORT HISTORY OF WEISS ENGINEERING After studying electrical engineering, Daniel Weiss joined the Willi Studer (Studer - Revox) company in Switzerland. His work included the design of a sampling frequency converter and of digital signal processing electronics for digital audio recorders. In 1985, Mr. Weiss founded the company Weiss Engineering Ltd. From the outset the company concentrated on the design and manufacture of digital audio equipment for mastering studios.
    [Show full text]