DOCSLIB.ORG

ESE 531: Digital Signal Processing Lecture Outline Downsampling

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
ESE 531: Digital Signal Processing Lecture Outline Downsampling Lecture Outline ESE 531: Digital Signal Processing ! Downsampling/Upsampling ! Practical Interpolation ! Non-integer Resampling Lec 10: February 14th, 2017 ! Multi-Rate Processing Practical and Non-integer Sampling, Multi- rate Sampling " Interchanging Operations ! Polyphase Decomposition ! Multi-Rate Filter Banks Penn ESE 531 Spring 2017 - Khanna Penn ESE 531 Spring 2017 - Khanna 2 Downsampling Downsampling ! Definition: Reducing the sampling rate by an integer number Penn ESE 531 Spring 2017 - Khanna 3 Penn ESE 531 Spring 2017 - Khanna 4 Example Example 2π 4π 2π 4π 6π Penn ESE 531 Spring 2017 - Khanna 5 Penn ESE 531 Spring 2017 - Khanna 6 1 Example Example Penn ESE 531 Spring 2017 - Khanna 7 Penn ESE 531 Spring 2017 - Khanna 8 Upsampling Upsampling ! Definition: Increasing the sampling rate by an integer number x[n] = xc (nT ) xi[n] = xc (nT ') xi[n] Penn ESE 531 Spring 2017 - Khanna 9 Penn ESE 531 Spring 2017 - Khanna 10 Frequency Domain Interpretation Frequency Domain Interpretation Penn ESE 531 Spring 2017 - Khanna 11 Penn ESE 531 Spring 2017 - Khanna 12 2 Example Example Penn ESE 531 Spring 2017 - Khanna 13 Penn ESE 531 Spring 2017 - Khanna 14 Example Example Penn ESE 531 Spring 2017 - Khanna 15 Penn ESE 531 Spring 2017 - Khanna 16 Example Example Penn ESE 531 Spring 2017 - Khanna 17 Penn ESE 531 Spring 2017 - Khanna 18 3 Practical Interpolation Practical Interpolation ! Interpolate with simple, practical filters ! Interpolate with simple, practical filters " Linear interpolation – samples between original samples " Linear interpolation – samples between original samples fall on a straight line connecting the samples fall on a straight line connecting the samples " Convolve with triangle instead of sinc " Convolve with triangle instead of sinc Penn ESE 531 Spring 2017 - Khanna 19 Penn ESE 531 Spring 2017 - Khanna 20 Frequency Domain Interpretation Linear Interpolation -- Frequency Domain xi[n] = xe[n]∗hlin[n] LPF approx Penn ESE 531 Spring 2017 - Khanna 21 Penn ESE 531 Spring 2017 - Khanna 22 Linear Interpolation -- Frequency Domain Linear Interpolation -- Frequency Domain xi[n] = xe[n]∗hlin[n] xi[n] = xe[n]∗hlin[n] LPF LPF approx approx Penn ESE 531 Spring 2017 - Khanna 23 Penn ESE 531 Spring 2017 - Khanna 24 4 Non-integer Sampling Non-integer Sampling ! T’=TM/L ! T’=TM/L " Upsample by L, then downsample by M " Upsample by L, then downsample by M interpolator decimator interpolator decimator Penn ESE 531 Spring 2017 - Khanna 25 Penn ESE 531 Spring 2017 - Khanna 26 Example Example ! T’=3/2T # L=2, M=3 ! T’=3/2T # L=2, M=3 Penn ESE 531 Spring 2017 - Khanna 27 Penn ESE 531 Spring 2017 - Khanna 28 Non-integer Sampling Multi-Rate Signal Processing ! T’=TM/L ! What if we want to resample by 1.01T? " Downsample by M, then upsample by L? " Expand by L=100 interpolator decimator " Filter π/101 ($$$$$) " Downsample by M=101 ! Fortunately there are ways around it! " Called multi-rate " Uses compressors, expanders and filtering Penn ESE 531 Spring 2017 - Khanna 29 Penn ESE 531 Spring 2017 - Khanna 30 5 Interchanging Operations Interchanging Operations - Expander Upsampling Downsampling Upsampling -expanding in time -compressing in time -expanding in time -compressing in frequency -expanding in frequency -compressing in frequency ? Penn ESE 531 Spring 2017 - Khanna 31 Penn ESE 531 Spring 2017 - Khanna 32 Interchanging Operations - Expander Interchanging Operations - Expander Upsampling Upsampling -expanding in time -expanding in time -compressing in frequency -compressing in frequency ? ≠ Penn ESE 531 Spring 2017 - Khanna 33 Penn ESE 531 Spring 2017 - Khanna 34 Interchanging Operations - Expander Interchanging Operations - Compressor Upsampling Downsampling -expanding in time -compressing in time -compressing in frequency -expanding in frequency = = Penn ESE 531 Spring 2017 - Khanna 35 Penn ESE 531 Spring 2017 - Khanna 36 6 Interchanging Operations - Compressor Interchanging Operations - Compressor = = = Penn ESE 531 Spring 2017 - Khanna 37 Penn ESE 531 Spring 2017 - Khanna 38 Interchanging Operations - Compressor Interchanging Operations - Compressor = = = = After compressing Penn ESE 531 Spring 2017 - Khanna 39 Penn ESE 531 Spring 2017 - Khanna 40 Interchanging Operations - Summary Multi-Rate Signal Processing ! What if we want to resample by 1.01T? " Expand by L=100 Filter and expander Expander and expanded filter* " Filter π/101 ($$$$$) " Downsample by M=101 ! Fortunately there are ways around it! " Called multi-rate " Uses compressors, expanders and filtering Compressor and filter Expanded filter* and compressor *Expanded filter = expanded impulse response, compressed freq response Penn ESE 531 Spring 2017 - Khanna 41 Penn ESE 531 Spring 2017 - Khanna 42 7 Polyphase Decomposition Polyphase Decomposition ! We can decompose an impulse response (of our ! We can decompose an impulse response (of our filter) to: filter) to: Penn ESE 531 Spring 2017 - Khanna 43 Penn ESE 531 Spring 2017 - Khanna 44 Polyphase Decomposition Polyphase Decomposition Penn ESE 531 Spring 2017 - Khanna 45 Penn ESE 531 Spring 2017 - Khanna 46 Polyphase Decomposition Polyphase Decomposition Penn ESE 531 Spring 2017 - Khanna 47 Penn ESE 531 Spring 2017 - Khanna 48 8 Polyphase Decomposition Polyphase Implementation of Decimation ! Problem: " Compute all y[n] and then throw away -- wasted computation! " For FIR length N # N mults/unit time Penn ESE 531 Spring 2017 - Khanna 49 Penn ESE 531 Spring 2017 - Khanna 50 Polyphase Implementation of Decimation Polyphase Implementation of Decimation Penn ESE 531 Spring 2017 - Khanna 51 Penn ESE 531 Spring 2017 - Khanna 52 Interchanging Operations - Summary Polyphase Implementation of Decimation Filter and expander Expander and expanded filter Compressor and filter Expanded filter and compressor Penn ESE 531 Spring 2017 - Khanna 53 Penn ESE 531 Spring 2017 - Khanna 54 9 Polyphase Implementation of Decimation Multi-Rate Signal Processing ! What if we want to resample by 1.01T? " Expand by L=100 " Filter π/101 ($$$$$) Each filter computation: -N/M multiplications " Downsample by M=101 -1/M rate per sample #N/M*(1/M) mults/unit time ! Fortunately there are ways around it! " Called multi-rate " Uses compressors, expanders and filtering Total computation: -M filters #N/M mults/unit time Penn ESE 531 Spring 2017 - Khanna 55 Penn ESE 531 Spring 2017 - Khanna 56 Polyphase Implementation of Decimator Polyphase Implementation of Interpolation interpolator decimator interpolator decimator E0(z) E0(z) E0(z) Penn ESE 531 Spring 2017 - Khanna 57 Penn ESE 531 Spring 2017 - Khanna 58 Multi-Rate Filter Banks Multi-Rate Filter Banks ! Use filter banks to operate on a signal differently in ! Use filter banks to operate on a signal differently in different frequency bands different frequency bands " To save computation, reduce the rate after filtering " To save computation, reduce the rate after filtering ! h0[n] is low-pass, h1[n] is high-pass jπn " Often h1[n]=e h0[n] $ shift freq resp by π Penn ESE 531 Spring 2017 - Khanna 59 Penn ESE 531 Spring 2017 - Khanna 60 10 Multi-Rate Filter Banks Multi-Rate Filter Banks ! Assume h0, h1 are ideal low/high pass ! Assume h0, h1 are ideal low/high pass Penn ESE 531 Spring 2017 - Khanna 61 Penn ESE 531 Spring 2017 - Khanna 62 Multi-Rate Filter Banks Multi-Rate Filter Banks ! Assume h0, h1 are ideal low/high pass ! Assume h0, h1 are ideal low/high pass Have to be careful with order! Penn ESE 531 Spring 2017 - Khanna 63 Penn ESE 531 Spring 2017 - Khanna 64 Multi-Rate Filter Banks Multi-Rate Filter Banks ! Assume h0, h1 are ideal low/high pass ! Assume h0, h1 are ideal low/high pass Penn ESE 531 Spring 2017 - Khanna 65 Penn ESE 531 Spring 2017 - Khanna 66 11 Multi-Rate Filter Banks Non Ideal Filters ! h0, h1 are NOT ideal low/high pass ! h0, h1 are NOT ideal low/high pass Penn ESE 531 Spring 2017 - Khanna 67 Penn ESE 531 Spring 2017 - Khanna 68 Non Ideal Filters Perfect Reconstruction non-Ideal Filters Penn ESE 531 Spring 2017 - Khanna 69 Penn ESE 531 Spring 2017 - Khanna 70 Quadrature Mirror Filters Big Ideas ! Downsampling/Upsampling ! Practical Interpolation ! Non-integer Resampling ! Multi-Rate Processing Quadrature mirror filters " Interchanging Operations ! Polyphase Decomposition ! Multi-Rate Filter Banks Penn ESE 531 Spring 2017 - Khanna 71 Penn ESE 531 Spring 2017 - Khanna 72 12 Admin ! HW 4 due Friday " Typo in code in MATLAB problem, corrected handout " See Piazza for more information Penn ESE 531 Spring 2017 - Khanna 73 13 .
Load more

Recommended publications
  • Detection and Estimation Theory Introduction to ECE 531 Mojtaba Soltanalian- UIC the Course
    Detection and Estimation Theory Introduction to ECE 531 Mojtaba Soltanalian- UIC The course Lectures are given Tuesdays and Thursdays, 2:00-3:15pm Office hours: Thursdays 3:45-5:00pm, SEO 1031 Instructor: Prof. Mojtaba Soltanalian office: SEO 1031 email: [email protected] web: http://msol.people.uic.edu/ The course Course webpage: http://msol.people.uic.edu/ECE531 Textbook(s): * Fundamentals of Statistical Signal Processing, Volume 1: Estimation Theory, by Steven M. Kay, Prentice Hall, 1993, and (possibly) * Fundamentals of Statistical Signal Processing, Volume 2: Detection Theory, by Steven M. Kay, Prentice Hall 1998, available in hard copy form at the UIC Bookstore. The course Style: /Graduate Course with Active Participation/ Introduction Let’s start with a radar example! Introduction> Radar Example QUIZ Introduction> Radar Example You can actually explain it in ten seconds! Introduction> Radar Example Applications in Transportation, Defense, Medical Imaging, Life Sciences, Weather Prediction, Tracking & Localization Introduction> Radar Example The strongest signals leaking off our planet are radar transmissions, not television or radio. The most powerful radars, such as the one mounted on the Arecibo telescope (used to study the ionosphere and map asteroids) could be detected with a similarly sized antenna at a distance of nearly 1,000 light-years. - Seth Shostak, SETI Introduction> Estimation Traditionally discussed in STATISTICS. Estimation in Signal Processing: Digital Computers ADC/DAC (Sampling) Signal/Information Processing Introduction> Estimation The primary focus is on obtaining optimal estimation algorithms that may be implemented on a digital computer. We will work on digital signals/datasets which are typically samples of a continuous-time waveform.
    [Show full text]
  • Designing Commutative Cascades of Multidimensional Upsamplers And
    IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 0 Designing Commutative Cascades of Multidimensional Upsamplers and Downsamplers Brian L. Evans, Member, IEEE Abstract In multiple dimensions, the cascade of an upsampler by L and a downsampler by L commutes if and only if the integer matrices L and M are right coprime and LM = ML. This pap er presents algorithms to design L and M that yield commutative upsampler/dowsampler cascades. We prove that commutativity is p ossible if the 1 Jordan canonical form of the rational resampling matrix R = LM is equivalent to the Smith-McMillan form of R. A necessary condition for this equivalence is that R has an eigendecomp osition and the eigenvalues are rational. B. L. Evans is with the Department of Electrical and Computer Engineering, The UniversityofTexas at Austin, Austin, TX 78712-1084, USA. E-mail: [email protected], Web: http://www.ece.utexas.edu/~b evans, Phone: 512 232-1457, Fax: 512 471-5907. This work was sp onsored in part by NSF CAREER Award under Grant MIP-9702707. July 31, 1997 DRAFT IEEE SIGNAL PROCESSING LETTERS: SPL.SP.4.1 THEORY, ALGORITHMS, AND SYSTEMS 1 I. Introduction 1 Resampling systems scale the sampling rate by a rational factor R = L=M = LM , or 1 equivalently decimate by H = M=L = L M [1], by essentially upsampling by L, ltering, and downsampling by M . In converting compact disc data sampled at 44.1 kHz to digital audio tap e 48000 Hz 160 data sampled at 48 kHz, R = = . Because we can always factor R into coprime 44100 Hz 147 integers L and M , we can always commute the upsampler and downsampler which leads to ecient p olyphase structures of the resampling system.
    [Show full text]
  • Z-Transformation - I
    Digital signal processing: Lecture 5 z-transformation - I Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/1 Review of last lecture • Fourier transform & inverse Fourier transform: – Time domain & Frequency domain representations • Understand the “true face” (latent factor) of some physical phenomenon. – Key points: • Definition of Fourier transformation. • Definition of inverse Fourier transformation. • Condition for a signal to have FT. Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/2 Review of last lecture • The sampling theorem – If the highest frequency component contained in an analog signal is f0, the sampling frequency (the Nyquist rate) should be 2xf0 at least. • Frequency response of an LTI system: – The Fourier transformation of the impulse response – Physical meaning: frequency components to keep (~1) and those to remove (~0). – Theoretic foundation: Convolution theorem. Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/3 Topics of this lecture Chapter 6 of the textbook • The z-transformation. • z－変換 • Convergence region of z- • z－変換の収束領域 transform. －変換とフーリエ変換 • Relation between z- • z transform and Fourier • z－変換と差分方程式 transform. • 伝達関数 or システム • Relation between z- 関数 transform and difference equation. • Transfer function (system function). Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/4 z-transformation（z-変換） • Laplace transformation is important for analyzing analog signal/systems. • z-transformation is important for analyzing discrete signal/systems. • For a given signal x(n), its z-transformation is defined by ∞ Z[x(n)] = X (z) = ∑ x(n)z−n (6.3) n=0 where z is a complex variable. Produced by Qiangfu Zhao (Since 1995), All rights reserved © DSP-Lec05/5 One-sided z-transform and two-sided z-transform • The z-transform defined above is called one- sided z-transform (片側ｚ-変換）.
    [Show full text]
  • Basics on Digital Signal Processing
    Basics on Digital Signal Processing z - transform - Digital Filters Vassilis Anastassopoulos Electronics Laboratory, Physics Department, University of Patras Outline of the Lecture 1. The z-transform 2. Properties 3. Examples 4. Digital filters 5. Design of IIR and FIR filters 6. Linear phase 2/31 z-Transform 2 N 1 N 1 j nk n X (k) x(n) e N X (z) x(n) z n0 n0 Time to frequency Time to z-domain (complex) Transformation tool is the Transformation tool is complex wave z e j e j j j2k / N e e With amplitude ρ changing(?) with time With amplitude |ejω|=1 The z-transform is more general than the DFT 3/31 z-Transform For z=ejω i.e. ρ=1 we work on the N 1 unit circle X (z) x(n) z n And the z-transform degenerates n0 into the Fourier transform. I -z z=R+jI |z|=1 R The DFT is an expression of the z-transform on the unit circle. The quantity X(z) must exist with finite value on the unit circle i.e. must posses spectrum with which we can describe a signal or a system. 4/31 z-Transform convergence We are interested in those values of z for which X(z) converges. This region should contain the unit circle. I Why is it so? |a| N 1 N 1 X (z) x(n) zn x(n) (1/zn ) n0 n0 R At z=0, X(z) diverges ROC The values of z for which X(z) diverges are called poles of X(z).
    [Show full text]
  • 3F3 – Digital Signal Processing (DSP)
    3F3 – Digital Signal Processing (DSP) Simon Godsill www-sigproc.eng.cam.ac.uk/~sjg/teaching/3F3 Course Overview • 11 Lectures • Topics: – Digital Signal Processing – DFT, FFT – Digital Filters – Filter Design – Filter Implementation – Random signals – Optimal Filtering – Signal Modelling • Books: – J.G. Proakis and D.G. Manolakis, Digital Signal Processing 3rd edition, Prentice-Hall. – Statistical digital signal processing and modeling -Monson H. Hayes –Wiley • Some material adapted from courses by Dr. Malcolm Macleod, Prof. Peter Rayner and Dr. Arnaud Doucet Digital Signal Processing - Introduction • Digital signal processing (DSP) is the generic term for techniques such as filtering or spectrum analysis applied to digitally sampled signals. • Recall from 1B Signal and Data Analysis that the procedure is as shown below: • is the sampling period • is the sampling frequency • Recall also that low-pass anti-aliasing filters must be applied before A/D and D/A conversion in order to remove distortion from frequency components higher than Hz (see later for revision of this). • Digital signals are signals which are sampled in time (“discrete time”) and quantised. • Mathematical analysis of inherently digital signals (e.g. sunspot data, tide data) was developed by Gauss (1800), Schuster (1896) and many others since. • Electronic digital signal processing (DSP) was first extensively applied in geophysics (for oil-exploration) then military applications, and is now fundamental to communications, mobile devices, broadcasting, and most applications of signal and image processing. There are many advantages in carrying out digital rather than analogue processing; among these are flexibility and repeatability. The flexibility stems from the fact that system parameters are simply numbers stored in the processor.
    [Show full text]
  • CONVOLUTION: Digital Signal Processing .R .Hamming, W
    CONVOLUTION: Digital Signal Processing AN-237 National Semiconductor CONVOLUTION: Digital Application Note 237 Signal Processing January 1980 Introduction As digital signal processing continues to emerge as a major Decreasing the pulse width while increasing the pulse discipline in the field of electrical engineering, an even height to allow the area under the pulse to remain constant, greater demand has evolved to understand the basic theo- Figure 1c, shows from eq(1) and eq(2) the bandwidth or retical concepts involved in the development of varied and spectral-frequency content of the pulse to have increased, diverse signal processing systems. The most fundamental Figure 1d. concepts employed are (not necessarily listed in the order Further altering the pulse to that of Figure 1e provides for an [ ] of importance) the sampling theorem 1 , Fourier transforms even broader bandwidth, Figure 1f. If the pulse is finally al- [ ][] 2 3, convolution, covariance, etc. tered to the limit, i.e., the pulsewidth being infinitely narrow The intent of this article will be to address the concept of and its amplitude adjusted to still maintain an area of unity convolution and to present it in an introductory manner under the pulse, it is found in 1g and 1h the unit impulse hopefully easily understood by those entering the field of produces a constant, or ``flat'' spectrum equal to 1 at all digital signal processing. frequencies. Note that if ATe1 (unit area), we get, by defini- It may be appropriate to note that this article is Part II (Part I tion, the unit impulse function in time.
    [Show full text]
  • The Scientist and Engineer's Guide to Digital Signal Processing Properties of Convolution
    CHAPTER 7 Properties of Convolution A linear system's characteristics are completely specified by the system's impulse response, as governed by the mathematics of convolution. This is the basis of many signal processing techniques. For example: Digital filters are created by designing an appropriate impulse response. Enemy aircraft are detected with radar by analyzing a measured impulse response. Echo suppression in long distance telephone calls is accomplished by creating an impulse response that counteracts the impulse response of the reverberation. The list goes on and on. This chapter expands on the properties and usage of convolution in several areas. First, several common impulse responses are discussed. Second, methods are presented for dealing with cascade and parallel combinations of linear systems. Third, the technique of correlation is introduced. Fourth, a nasty problem with convolution is examined, the computation time can be unacceptably long using conventional algorithms and computers. Common Impulse Responses Delta Function The simplest impulse response is nothing more that a delta function, as shown in Fig. 7-1a. That is, an impulse on the input produces an identical impulse on the output. This means that all signals are passed through the system without change. Convolving any signal with a delta function results in exactly the same signal. Mathematically, this is written: EQUATION 7-1 The delta function is the identity for ( ' convolution. Any signal convolved with x[n] *[n] x[n] a delta function is left unchanged. This property makes the delta function the identity for convolution. This is analogous to zero being the identity for addition (a%0 ' a), and one being the identity for multiplication (a×1 ' a).
    [Show full text]
  • Exploring Anti-Aliasing Filters in Signal Conditioners for Mixed-Signal, Multimodal Sensor Conditioning by Arun T
    Texas Instruments Incorporated Amplifiers: Op Amps Exploring anti-aliasing filters in signal conditioners for mixed-signal, multimodal sensor conditioning By Arun T. Vemuri Systems Architect, Enhanced Industrial Introduction Figure 1. Multimodal, mixed-signal sensor-signal conditioner Some sensor-signal conditioners are used to process the output Analog Digital of multiple sense elements. This Domain Domain processing is often provided by multimodal, mixed-signal condi- tioners that can handle the out- puts from several sense elements Sense Digital Amplifier 1 ADC 1 at the same time. This article Element 1 Filter 1 analyzes the operation of anti- Processed aliasing filters in such sensor- Intelligent Output Compensation signal conditioners. Sense Digital Basics of sensor-signal Amplifier 2 ADC 2 Element 2 Filter 2 conditioners Sense elements, or transducers, convert a physical quantity of interest into electrical signals. Examples include piezo resistive bridges used to measure pres- sure, piezoelectric transducers used to detect ultrasonic than one sense element is processed by the same signal waves, and electrochemical cells used to measure gas conditioner is called multimodal signal conditioning. concentrations. The electrical signals produced by sense Mixed-signal signal conditioning elements are small and exhibit nonidealities, such as tem- Another aspect of sensor-signal conditioning is the electri- perature drifts and nonlinear transfer functions. cal domain in which the signal conditioning occurs. TI’s Sensor analog front ends such as the Texas Instruments PGA309 is an example of a device where the signal condi- (TI) LMP91000 and sensor-signal conditioners such as TI’s tioning of resistive-bridge sense elements occurs in the PGA400/450 are used to amplify the small signals produced analog domain.
    [Show full text]
  • Digital Signal Processing: Theory and Practice, Hardware and Software
    AC 2009-959: DIGITAL SIGNAL PROCESSING: THEORY AND PRACTICE, HARDWARE AND SOFTWARE Wei PAN, Idaho State University Wei Pan is Assistant Professor and Director of VLSI Laboratory, Electrical Engineering Department, Idaho State University. She has several years of industrial experience including Siemens (project engineering/management.) Dr. Pan is an active member of ASEE and IEEE and serves on the membership committee of the IEEE Education Society. S. Hossein Mousavinezhad, Idaho State University S. Hossein Mousavinezhad is Professor and Chair, Electrical Engineering Department, Idaho State University. Dr. Mousavinezhad is active in ASEE and IEEE and is an ABET program evaluator. Hossein is the founding general chair of the IEEE International Conferences on Electro Information Technology. Kenyon Hart, Idaho State University Kenyon Hart is Specialist Engineer and Associate Lecturer, Electrical Engineering Department, Idaho State University, Pocatello, Idaho. Page 14.491.1 Page © American Society for Engineering Education, 2009 Digital Signal Processing, Theory/Practice, HW/SW Abstract Digital Signal Processing (DSP) is a course offered by many Electrical and Computer Engineering (ECE) programs. In our school we offer a senior-level, first-year graduate course with both lecture and laboratory sections. Our experience has shown that some students consider the subject matter to be too theoretical, relying heavily on mathematical concepts and abstraction. There are several visible applications of DSP including: cellular communication systems, digital image processing and biomedical signal processing. Authors have incorporated many examples utilizing software packages including MATLAB/MATHCAD in the course and also used classroom demonstrations to help students visualize some difficult (but important) concepts such as digital filters and their design, various signal transformations, convolution, difference equations modeling, signals/systems classifications and power spectral estimation as well as optimal filters.
    [Show full text]
  • Deep Image Prior for Undersampling High-Speed Photoacoustic Microscopy
    Photoacoustics 22 (2021) 100266 Contents lists available at ScienceDirect Photoacoustics journal homepage: www.elsevier.com/locate/pacs Deep image prior for undersampling high-speed photoacoustic microscopy Tri Vu a,*, Anthony DiSpirito III a, Daiwei Li a, Zixuan Wang c, Xiaoyi Zhu a, Maomao Chen a, Laiming Jiang d, Dong Zhang b, Jianwen Luo b, Yu Shrike Zhang c, Qifa Zhou d, Roarke Horstmeyer e, Junjie Yao a a Photoacoustic Imaging Lab, Duke University, Durham, NC, 27708, USA b Department of Biomedical Engineering, Tsinghua University, Beijing, 100084, China c Division of Engineering in Medicine, Department of Medicine, Brigham and Women’s Hospital, Harvard Medical School, Cambridge, MA, 02139, USA d Department of Biomedical Engineering and USC Roski Eye Institute, University of Southern California, Los Angeles, CA, 90089, USA e Computational Optics Lab, Duke University, Durham, NC, 27708, USA ARTICLE INFO ABSTRACT Keywords: Photoacoustic microscopy (PAM) is an emerging imaging method combining light and sound. However, limited Convolutional neural network by the laser’s repetition rate, state-of-the-art high-speed PAM technology often sacrificesspatial sampling density Deep image prior (i.e., undersampling) for increased imaging speed over a large field-of-view. Deep learning (DL) methods have Deep learning recently been used to improve sparsely sampled PAM images; however, these methods often require time- High-speed imaging consuming pre-training and large training dataset with ground truth. Here, we propose the use of deep image Photoacoustic microscopy Raster scanning prior (DIP) to improve the image quality of undersampled PAM images. Unlike other DL approaches, DIP requires Undersampling neither pre-training nor fully-sampled ground truth, enabling its flexible and fast implementation on various imaging targets.
    [Show full text]
  • ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform
    Department of Electrical Engineering University of Arkansas ELEG 5173L Digital Signal Processing Ch. 3 Discrete-Time Fourier Transform Dr. Jingxian Wu [email protected] 2 OUTLINE • The Discrete-Time Fourier Transform (DTFT) • Properties • DTFT of Sampled Signals • Upsampling and downsampling 3 DTFT • Discrete-time Fourier Transform (DTFT) X () x(n)e jn n – (radians): digital frequency • Review: Z-transform: X (z) x(n)zn n0 j X () X (z) | j – Replace z with e . ze • Review: Fourier transform: X () x(t)e jt – (rads/sec): analog frequency 4 DTFT • Relationship between DTFT and Fourier Transform – Sample a continuous time signal x a ( t ) with a sampling period T xs (t) xa (t) (t nT ) xa (nT ) (t nT ) n n – The Fourier Transform of ys (t) jt jnT X s () xs (t)e dt xa (nT)e n – Define: T • : digital frequency (unit: radians) • : analog frequency (unit: radians/sec) – Let x(n) xa (nT) X () X s T 5 DTFT • Relationship between DTFT and Fourier Transform (Cont’d) – The DTFT can be considered as the scaled version of the Fourier transform of the sampled continuous-time signal jt jnT X s () xs (t)e dt xa (nT)e n x(n) x (nT) T a jn X () X s x(n)e T n 6 DTFT • Discrete Frequency – Unit: radians (the unit of continuous frequency is radians/sec) – X ( ) is a periodic function with period 2 j2 n jn j2n jn X ( 2 ) x(n)e x(n)e e x(n)e X () n n n – We only need to consider for • For Fourier transform, we need to consider 1 – f T 2 2T 1 – f T 2 2T 7 DTFT • Example: find the DTFT of the following signal – 1.
    [Show full text]
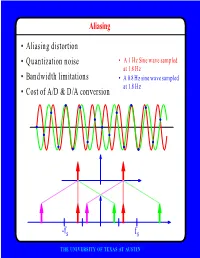
  • F • Aliasing Distortion • Quantization Noise • Bandwidth Limitations • Cost of A/D & D/A Conversion
    Aliasing • Aliasing distortion • Quantization noise • A 1 Hz Sine wave sampled at 1.8 Hz • Bandwidth limitations • A 0.8 Hz sine wave sampled at 1.8 Hz • Cost of A/D & D/A conversion -fs fs THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Perfect reconstruction of a Better trade-off between signal is possible even after bandwidth and noise severe distortion immunity performance digital analog bandwidth Increase signal-to-noise ratio simply by adding more bits SNR = -7.2 + 6 dB/bit THE UNIVERSITY OF TEXAS AT AUSTIN Advantages of Digital Systems Programmability • Modifiable in the field • Implement multiple standards • Better user interfaces • Tolerance for changes in specifications • Get better use of hardware for low-speed operations • Debugging • User programmability THE UNIVERSITY OF TEXAS AT AUSTIN Disadvantages of Digital Systems Programmability • Speed is too slow for some applications • High average power and peak power consumption RISC (2 Watts) vs. DSP (50 mW) DATA PROG MEMORY MEMORY HARVARD ARCHITECTURE • Aliasing from undersampling • Clipping from quantization Q[v] v v THE UNIVERSITY OF TEXAS AT AUSTIN Analog-to-Digital Conversion 1 --- T h(t) Q[.] xt() yt() ynT() yˆ()nT Anti-Aliasing Sampler Quantizer Filter xt() y(nT) t n y(t) ^y(nT) t n THE UNIVERSITY OF TEXAS AT AUSTIN Resampling Changing the Sampling Rate • Conversion between audio formats Compact 48.0 Digital Disc ---------- Audio Tape 44.1 KHz44.1 48 KHz • Speech compression Speech 1 Speech for on DAT --- Telephone 48 KHz 6 8 KHz • Video format conversion
    [Show full text]