DOCSLIB.ORG

31 Diffraction and Interference.Pdf

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
31 Diffraction and Interference.Pdf Diffraction and Interference Figu These expar new .5 wave oday Isaac Newton is most famous for his new v accomplishments in mechanics—his laws of Tmotion and universal gravitation. Early in his career, however, he was most famous for his work on light. Newton pictured light as a beam of ultra-tiny material particles. With this model he could explain reflection as a bouncing of the parti- cles from a surface, and he could explain refraction as the result of deflecting forces from the surface Interference colors. acting on the light particles. In the eighteenth and nineteenth cen- turies, this particle model gave way to a wave model of light because waves could explain not only reflection and refraction, but everything else that was known about light at that time. In this chapter we will investigate the wave aspects of light, which are needed to explain two important phenomena—diffraction and interference. As Huygens' Principle origin; 31.1 pie is I constr In the late 1600s a Dutch mathematician-scientist, Christian Huygens, dimen proposed a very interesting idea about waves. Huygens stated that light waves spreading out from a point source may be regarded as die overlapping of tiny secondary wavelets, and that every point on ' any wave front may be regarded as a new point source of secondary waves. We see this in Figure 31.1. In other words, wave fronts are A made up of tinier wave fronts. This idea is called Huygens' principle. Look at the spherical wave front in Figure 31.2. Each point along the wave front AN is the source of a new wavelet that spreads out in a sphere from that point. Only a few of the infinite number of wavelets are shown in the figure. The new wave front BB' can be regarded as a smooth surface enclosing the infinite number of over- lapping wavelets that started from AA' a short time earlier. 480 Chapter 31 Diffraction and Interference Figure 31.1 A These drawings are from Huygens' book Treatise on Light. Light from A (left) expands in wave fronts, every point of which (right) behaves as if it were a new source of waves. Secondary wavelets starting at to,13,b,12 form a new wave front (d,d,d,ch; secondary wavelets starting at d,d,d,d form still another new wave front (DCEF). 4 Figure 31.2 Huygens' principle applied to a spherical wave front. WAVE FRONT NEW WAVE FRONT As a wave front spreads, it appears less curved. Very far from the original source, the wave fronts seem to form a plane. A good exam- ple is the plane waves that arrive from the sun. A Huygens' wavelet construction for plane waves is shown in Figure 31.3. (In a two- dimensional drawing, the planes are shown as straight lines.) 4 Figure 31.3 WAVE FRONT Huygens' principle applied to a A plane wave front. / \ ll \ I a ---_.--,_____--_.--,____--.. - \ r NEW WAVE FRONT ‘‘‘ Figure 31.4 A Huygens' principle applied to (a) reflection and (b) refraction. Figuri Straigh The laws of reflection and refraction are illustrated via Huygens' openin. principle in Figure 31.4. You can observe Huygens' principle in water waves that are made to pass through a narrow opening. A wave with straight wave fronts can be generated in water by repeatedly dipping a stick lengthwise into the water (Figure 313;. A ruler works well. When the 31. straight wave fronts pass through the opening in a barrier, interest- ing wave patterns result. Any bt is calif of stra Figure 31.5 S is with Making plane waves in a tank of As the water and watching the pattern more they produce when they pass light though an opening in a barrier. the wa When a pica out likt is diffn When the opening is wide, you'll see straight wave fronts pass through without change—except at the corners, where the wave fronts are bent into the "shadow region" in accord with tiltiyg^^-' opening, less of the wave principle. If you narrow the width of the _ gets through, and the spreading into the shadow region is more pro- nounced. When the opening is small compared with the wavelength SI of the waves, Huygens' idea that every part of a wave front can be regarded as a source of new wavelets becomes quite apparent. As the waves move into the narrow opening, the water sloshing up and down in the opening is easily seen to act as a point source of circular other side of the barrier. The photos in waves that fan out on the Figuro Figure 31.6 are top views of water waves generated by a vibrating Lightfr c. stick. Note how the waves fan out more as the hole through which ig is they pass becomes smaller. ton it 482 Chapter 31 Diffraction and Interference ...i.umm.d..••••••••••1. ^ ..... Figure 31.6 A Straight waves passing through openings of various sizes. The smaller the opening, the greater the bending of the waves at the edges. 31.2 Diffraction Any bending of a wave by means other than reflection or refraction is called diffraction. The photos of Figure 31.6 show the diffraction of straight water waves through various openings. When the opening k wide compared with the wavelength, the spreading effect is small. • As the opening becomes narrower, the spreading of waves becomes more pronounced. The same occurs for all kinds of waves, including light waves. When light passes though an opening that is large compared with the wavelength of light, it casts a rather sharp shadow (Figure 31.7). When light passes through a small opening, such as a thin razor slit in a piece of opaque material, it casts a fuzzy shadow, for the light fans out like the water through the narrow opening in Figure 31.6. The light K" is diffracted by the thin slit. I I ;Si? LIGHT LIGHT SOURCE SOURCE WIDE WINDOW Figure 31.7 A J.ightcasts a sharp shadow with some fuzziness at its edges when the open- g is large compared with the wavelength of the light. Because of diffrac- ion, it casts a fuzzier shadow when the opening is extremely narrow. Diffraction is not confined to the spreading of light through narrow slits or other openings. Diffraction occurs to some degree for all shad- object ows On close examination, even the sharpest shadow is blurred at the ' waveli edge. When light is of a single color, diffraction can produce diffraction fractu fringes at the edge of the shadow, as shown in Figure 31.8.1n white light struct the fringes merge together to create a fuzzy blur at the edge of a shadow , amou The amount of diffraction depends on the size of the wavelength • defeat compared with the size of the obstruction that casts the shadow Tc (Figure 31.9). The longer the wave compared with the obstruction, hs the greater the diffraction is. Long waves are better at filling in shad- \gavel( ows. This is why foghorns emit low-frequency sound waves—to fill in than t "blind spots." Likewise for radio waves of the standard AM broadcast electri band. These are very long compared with the size of most objects in The d their path. Long waves don't "see" relatively small buildings in their that o path. They diffract, or bend, readily around buildings and reach Tl Figure 31.8 • more places than shorter waves do.* wave!' Diffraction fringes around the I011/11i scissors are evident in the shad- I 4 4 4 4 4 I 4 4 1 1 4 4 4 long-v ows of laser light which is of a in its s single frequency. These fringes of sho would be filled in by multitudes to doll of other fringes if the source gas-fl were white light • tumor the de the mi 4 4 devia a. b. C. Figure 31.9 A (a) Waves tend to spread into the shadow region. (b) When the wavelength is about the size of the object the shadow is soon filled in. (c) When the wave- length is short compared with the width of the object, a sharper shadow is cast. FM radio waves are shorter, don't diffract as much around build- ings, and aren't received as well as AM radio waves are in mountain canyons or city "canyons." This is why many localities have poor FM reception while AM reception comes in loud and clear. TV waves, which are also electromagnetic waves, behave much like FM waves." TV antennas are often put on rooftops to improve recep- tion. Both FM and TV transmission are "line of sight," meaning that diffraction is not significant, whereas AM transmission diffracts 'round hills and buildings to reach places that would othen,deo he shadowed. Diffraction can be helpful. * The ofte * On the other hand, a framework of connected steel girders in a building or bridge can an t act as a "polished" surface for long-wavelength radio waves, reflecting them away from the structure. That's why you lose reception when you drive onto a steel bridge rep while listening to an AM station. So although long waves get around a steel structure, phi, they don't get into it. aco dol ** Most TV channels have wavelengths shorter than FM wavelengths, and therefore even oft less diffraction than FM, but some (channels 2-6) have wavelengths longer than FM , COr wavelengths. Is 484 Chapter 31 Diffraction and Interference Diffraction is not so helpful when we wish to see very small objects with microscopes.
Load more

Recommended publications
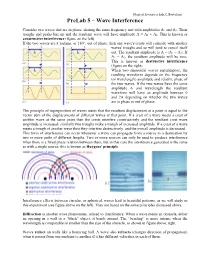
  • Prelab 5 – Wave Interference
    Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths.
    [Show full text]
  • Lecture 9, P 1 Lecture 9: Introduction to QM: Review and Examples
    Lecture 9, p 1 Lecture 9: Introduction to QM: Review and Examples S1 S2 Lecture 9, p 2 Photoelectric Effect Binding KE=⋅ eV = hf −Φ energy max stop Φ The work function: 3.5 Φ is the minimum energy needed to strip 3 an electron from the metal. 2.5 2 (v) Φ is defined as positive . 1.5 stop 1 Not all electrons will leave with the maximum V f0 kinetic energy (due to losses). 0.5 0 0 5 10 15 Conclusions: f (x10 14 Hz) • Light arrives in “packets” of energy (photons ). • Ephoton = hf • Increasing the intensity increases # photons, not the photon energy. Each photon ejects (at most) one electron from the metal. Recall: For EM waves, frequency and wavelength are related by f = c/ λ. Therefore: Ephoton = hc/ λ = 1240 eV-nm/ λ Lecture 9, p 3 Photoelectric Effect Example 1. When light of wavelength λ = 400 nm shines on lithium, the stopping voltage of the electrons is Vstop = 0.21 V . What is the work function of lithium? Lecture 9, p 4 Photoelectric Effect: Solution 1. When light of wavelength λ = 400 nm shines on lithium, the stopping voltage of the electrons is Vstop = 0.21 V . What is the work function of lithium? Φ = hf - eV stop Instead of hf, use hc/ λ: 1240/400 = 3.1 eV = 3.1eV - 0.21eV For Vstop = 0.21 V, eV stop = 0.21 eV = 2.89 eV Lecture 9, p 5 Act 1 3 1. If the workfunction of the material increased, (v) 2 how would the graph change? stop a.
    [Show full text]
  • Waves: Interference Instructions: Read Through the Information Below
    Pre-AP Physics Week 2: Day 1 Notes Waves: Interference Instructions: Read through the information below. Then answer the questions below. When two or more waves meet, they interact with each other. The interaction of waves with other waves is called wave interference. Wave interference may occur when two waves that are traveling in opposite directions meet. The two waves pass through each other, and this affects their amplitude. Amplitude is the maximum distance the particles of the medium move from their resting positions when a wave passes through. How amplitude is affected by wave interference depends on the type of interference. Interference can be constructive or destructive. Constructive Interference Destructive Interference Constructive interference occurs when crests of one Destructive interference occurs when the crests of one wave overlap the crests of the other wave. The figure wave overlap the troughs, or lowest points, of another above shows what happens. As the waves pass through wave. The figure above shows what happens. As the each other, the crests combine to produce a wave with waves pass through each other, the crests and troughs greater amplitude. The same can happen with two cancel each other out to produce a wave with zero troughs interacting. amplitude. (NOTE: They don’t always have to fully cancel out. Destructive interference can be partial cancellation.) TRUE or FALSE: Identify the following statements as being either true (T) or false (F). 1. When two pulses meet up with each other while moving through the same medium, they tend to bounce off each other and return back to their origin.
    [Show full text]
  • Time-Domain Grating with a Periodically Driven Qutrit
    PHYSICAL REVIEW APPLIED 11, 014053 (2019) Time-Domain Grating with a Periodically Driven Qutrit Yingying Han,1,2,3,§ Xiao-Qing Luo,2,3,§ Tie-Fu Li,4,2,* Wenxian Zhang,1,† Shuai-Peng Wang,2 J.S. Tsai,5,6 Franco Nori,5,7 and J.Q. You3,2,‡ 1 School of Physics and Technology, Wuhan University, Wuhan, Hubei 430072, China 2 Quantum Physics and Quantum Information Division, Beijing Computational Science Research Center, Beijing 100193, China 3 Interdisciplinary Center of Quantum Information and Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics and State Key Laboratory of Modern Optical Instrumentation, Zhejiang University, Hangzhou 310027, China 4 Institute of Microelectronics, Department of Microelectronics and Nanoelectronics, and Tsinghua National Laboratory of Information Science and Technology, Tsinghua University, Beijing 100084, China 5 Theoretical Quantum Physics Laboratory, RIKEN Cluster for Pioneering Research, Wako-shi, Saitama 351-0198, Japan 6 Department of Physic, Tokyo University of Science, Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan 7 Department of Physics, The University of Michigan, Ann Arbor, Michigan 48109-1040, USA (Received 23 October 2018; revised manuscript received 3 December 2018; published 28 January 2019) Physical systems in the time domain may exhibit analogous phenomena in real space, such as time crystals, time-domain Fresnel lenses, and modulational interference in a qubit. Here, we report the experi- mental realization of time-domain grating using a superconducting qutrit in periodically modulated probe and control fields via two schemes: simultaneous modulation and complementary modulation. Both exper- imental and numerical results exhibit modulated Autler-Townes (AT) and modulation-induced diffraction (MID) effects.
    [Show full text]
  • Physical Quantum States and the Meaning of Probability Michel Paty
    Physical quantum states and the meaning of probability Michel Paty To cite this version: Michel Paty. Physical quantum states and the meaning of probability. Galavotti, Maria Carla, Suppes, Patrick and Costantini, Domenico. Stochastic Causality, CSLI Publications (Center for Studies on Language and Information), Stanford (Ca, USA), p. 235-255, 2001. halshs-00187887 HAL Id: halshs-00187887 https://halshs.archives-ouvertes.fr/halshs-00187887 Submitted on 15 Nov 2007 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. as Chapter 14, in Galavotti, Maria Carla, Suppes, Patrick and Costantini, Domenico, (eds.), Stochastic Causality, CSLI Publications (Center for Studies on Language and Information), Stanford (Ca, USA), 2001, p. 235-255. Physical quantum states and the meaning of probability* Michel Paty Ëquipe REHSEIS (UMR 7596), CNRS & Université Paris 7-Denis Diderot, 37 rue Jacob, F-75006 Paris, France. E-mail : [email protected] Abstract. We investigate epistemologically the meaning of probability as implied in quantum physics in connection with a proposed direct interpretation of the state function and of the related quantum theoretical quantities in terms of physical systems having physical properties, through an extension of meaning of the notion of physical quantity to complex mathematical expressions not reductible to simple numerical values.
    [Show full text]
  • When the Uncertainty Principle Goes to 11... Or How to Explain Quantum Physics with Heavy Metal
    Ronald E. Hatcher Science on Saturday Lecture Series 12 January 2019 When The Uncertainty Principle goes to 11... or How to Explain Quantum Physics with Heavy Metal Philip Moriarty Professor, University of Nottingham, United Kingdom ABSTRACT: There are deep and fundamental linKs between quantum physics and heavy metal. No, really. There are. Far from being music for Neanderthals, as it’s too often construed, metal can be harmonically and rhythmically complex. That complexity is the source of many connections to the quantum world. You’ll discover how the Heisenberg uncertainty principle comes into play with every chugging guitar riff, what wave interference has to do with Iron Maiden, and why metalheads in mosh pits behave just liKe molecules in a gas. BIOGRAPHY: Philip Moriarty is a professor of physics, a heavy metal fan, a Keen air-drummer, and author of “When The Uncertainty Principle Goes To 11 (or How To Explain Quantum Physics With Heavy Metal” (Ben Bella 2018). His research at the University of Nottingham focuses on prodding, pushing, and poKing single atoms and molecules; in this nanoscopic world, quantum physics is all. Moriarty has taught physics for twenty years and has always been strucK by the number of students in his classes who profess a love of metal music, and by the deep connections between heavy metal and quantum mechanics. A frequent contributor to the Sixty Symbols YouTube channel, which won the Institute of Physics’ Kelvin Award in 2016 for “for innovative and effective promotion of the public understanding of physics”, he has a Keen interest in public engagement, outreach, and bridging the arts-science divide.
    [Show full text]
  • Rethinking a Delayed Choice Quantum Eraser Experiment: a Simple Baseball Model Jeffrey H
    PHYSICS ESSAYS 26, 1 (2013) Rethinking a delayed choice quantum eraser experiment: A simple baseball model Jeffrey H. Boyda) 57 Woods Road, Bethany, Connecticut 06524, USA (Received 10 June 2012; accepted 26 December 2012; published online 26 February 2013) Abstract: In a double slit experiment, you can see an interference fringe pattern or you can know which slit the photon came through, but not both. There are two diametrically opposite theories about why this happens. One is complementarity. The other is the proposal made in this article. An experiment, published in 2000 [Y.-H. Kim et al., Phys. Rev. Lett. 8, 1 (2000)] allegedly supports the idea of complementarity. With different starting assumptions, we arrive at opposite conclusions: complementarity is irrelevant to this experiment. Our assumptions come from the Theory of Elementary Waves. Waves are assumed to travel in the opposite direction: from the detector to the laser. All wave interference is located at the laser. All decisions of importance are located at the laser, not at the detectors. The “decisions” concern which of several elementary rays a photon chooses to follow (this is a probabilistic decision). If a photon is emitted in response to one such impinging ray, all wave interference is then complete. The photon will follow backwards that ray alone, with a probability of one, back to the pair of detectors from which that ray originated. Based on these assumptions, the experiment has nothing to do with complementarity. There is also no delayed choice and no quantum eraser. Conclusion: complementarity is not the only way to understand this experiment.
    [Show full text]
  • Revisiting Self-Interference in Young's Double-Slit Experiments
    Revisiting self-interference in Young’s double-slit experiments S. Kim1 and Byoung S. Ham1,* 1Center for Photon Information Processing, School of Electrical Engineering and Computer Science, Gwangju Institute of Science and Technology 123 Chumdangwagi-ro, Buk-gu, Gwangju 61005, South Korea (Submitted on April. 16, 2021 *[email protected]) Abstract: Over the past several decades, single photon-based path interference in Young’s double-slit experiment has been well demonstrated for the particle nature of photons satisfying complementarity theory, where the quantum mechanical interpretation of the single photon interference fringe is given by Born’s rule for complex amplitudes in measurements. Unlike most conventional methods using entangled photon pairs, here, a classical coherent light source is directly applied for the proof of the same self-interference phenomenon. Instead of Young’s double slits, we use a Mach-Zehnder interferometer as usual, where the resulting self-interference fringe of coherent single photons is exactly the same as that of the coherent photon ensemble of the laser, demonstrating that the classical coherence based on the wave nature is rooted in the single photon self- interference. This unexpected result seems to contradict our common understanding of decoherence phenomena caused by multi-wave interference among bandwidth distributed photons in coherence optics. Introduction Young’s double-slit experiments [1] have been studied over the last century using not only the wave nature of coherent light but also the particle nature of electrons [2-4], atoms [5,6], and photons [7-10] for quantum mechanical understanding of self-interference (SI) [11,12]. According to the Copenhagen interpretation, a single photon can be viewed as either a particle nature or a wave nature, so that the Young’s double-slit interference fringe based on single photons has been interpreted as self-interference based on the wave nature, satisfying the complementarity theory [13].
    [Show full text]
  • The Concept of the Photon—Revisited
    The concept of the photon—revisited Ashok Muthukrishnan,1 Marlan O. Scully,1,2 and M. Suhail Zubairy1,3 1Institute for Quantum Studies and Department of Physics, Texas A&M University, College Station, TX 77843 2Departments of Chemistry and Aerospace and Mechanical Engineering, Princeton University, Princeton, NJ 08544 3Department of Electronics, Quaid-i-Azam University, Islamabad, Pakistan The photon concept is one of the most debated issues in the history of physical science. Some thirty years ago, we published an article in Physics Today entitled “The Concept of the Photon,”1 in which we described the “photon” as a classical electromagnetic field plus the fluctuations associated with the vacuum. However, subsequent developments required us to envision the photon as an intrinsically quantum mechanical entity, whose basic physics is much deeper than can be explained by the simple ‘classical wave plus vacuum fluctuations’ picture. These ideas and the extensions of our conceptual understanding are discussed in detail in our recent quantum optics book.2 In this article we revisit the photon concept based on examples from these sources and more. © 2003 Optical Society of America OCIS codes: 270.0270, 260.0260. he “photon” is a quintessentially twentieth-century con- on are vacuum fluctuations (as in our earlier article1), and as- Tcept, intimately tied to the birth of quantum mechanics pects of many-particle correlations (as in our recent book2). and quantum electrodynamics. However, the root of the idea Examples of the first are spontaneous emission, Lamb shift, may be said to be much older, as old as the historical debate and the scattering of atoms off the vacuum field at the en- on the nature of light itself – whether it is a wave or a particle trance to a micromaser.
    [Show full text]
  • Arxiv:2012.09463V1 [Quant-Ph] 17 Dec 2020 Have Also Been Studied
    Long-range connectivity in a superconducting quantum processor using a ring resonator Sumeru Hazra,1 Anirban Bhattacharjee,1 Madhavi Chand,1 Kishor V. Salunkhe,1, Sriram Gopalakrishnan,∗ Meghan P. Patankar,1, and R. Vijay1y 1Department of Condensed Matter Physics and Materials Science, Tata Institute of Fundamental Research, 1 Homi Bhabha Road, Mumbai 400005, India (Dated: December 18, 2020) Qubit coherence and gate fidelity are typically considered the two most important metrics for characterizing a quantum processor. An equally important metric is inter-qubit connectivity as it minimizes gate count and allows implementing algorithms efficiently with reduced error. However, inter-qubit connectivity in superconducting processors tends to be limited to nearest neighbour due to practical constraints in the physical realization. Here, we introduce a novel superconducting architecture that uses a ring resonator as a multi-path coupling element with the qubits uniformly distributed throughout its circumference. Our planar design provides significant enhancement in connectivity over state of the art superconducting processors without any additional fabrication complexity. We theoretically analyse the qubit connectivity and experimentally verify it in a device capable of supporting up to twelve qubits where each qubit can be connected to nine other qubits. Our concept is scalable, adaptable to other platforms and has the potential to significantly accelerate progress in quantum computing, annealing, simulations and error correction. I. INTRODUCTION While recent experiments[5, 14] have implemented all- to-all connectivity by using a single bus resonator with Quantum information processors promise tremendous many superconducting qubits connected at its anti-nodes computational advantages in solving a broad class of (Fig.
    [Show full text]
  • Chapter 37 Interference of Light Waves
    Chapter 37 Interference of Light Waves CHAPTER OUTLINE 37.1 Conditions for Interference 37.2 Young’s Double-Slit Experiment 37.3 Intensity Distribution of the Double-Slit Interference Pattern 37.4 Phasor Addition of Waves 37.5 Change of Phase Due to Reflection 37.6 Interference in Thin Films 37.7 The Michelson Interferometer L The colors in many of a hummingbird’s feathers are not due to pigment. The iridescence that makes the brilliant colors that often appear on the throat and belly is due to an interference effect caused by structures in the feathers. The colors will vary with the viewing angle. (RO-MA/Index Stock Imagery) 1176 In the preceding chapter, we used light rays to examine what happens when light passes through a lens or reflects from a mirror. This discussion completed our study of geometric optics. Here in Chapter 37 and in the next chapter, we are concerned with wave optics or physical optics, the study of interference, diffraction, and polarization of light. These phenomena cannot be adequately explained with the ray optics used in Chapters 35 and 36. We now learn how treating light as waves rather than as rays leads to a satisfying description of such phenomena. 37.1 Conditions for Interference In Chapter 18, we found that the superposition of two mechanical waves can be constructive or destructive. In constructive interference, the amplitude of the resultant wave at a given position or time is greater than that of either individual wave, whereas in destructive interference, the resultant amplitude is less than that of either individual wave.
    [Show full text]
  • Parpcle Duality, Probability and Uncertainty-‐ Principle
    Ch 38. Wave-Par.cle Duality, Probability and Uncertainty- Principle Ph274 – Modern Physics 2/29/2016 Prof. Pui Lam Learning Outcomes (1) Understand the “Principle of Complementarity” (2) Understand how wave interference paern can be interpreted as probability of a photon landing on the screen. (3) Understand the “Uncertainty Principle” Principle of Complementarity • “The wave descrip.ons and the par.cle descrip.ons are complementary. That is, we need both to complete our model of nature, but will never need to use both at the same .me to describe a single part of an occurrence.” • Note: Although we never need to use both at the same .me to describe a single part of an occurrence, some results can be explained by either the wave or par.cle descrip.on, see next slide for an example. Diffrac.on at very low intensity – introduce the concept of probabilis.c mo.on • Consider performing a single slit diffrac.on with light intensity so low that prac.cally only one photon going through the slit at a .me. • According to quantum theory, aer the photon exit the slit, its momentum is uncertain (Uncertainty Principle). The photon can exit at any angle with some probability. • If we collect the photons over a period .me, the resul.ng probabilis.c paern resembles the diffrac.on paern from wave theory. • BoRom line: At the quantum scale, mo.ons are probabilis.c. Quantum theory provides a method to calculate the probability. Figure 38.16 Uncertainty Principle • Use single slit diffrac.on as an example: • Slit width =a, that means the locaon of the photon in the “y-direc.on” can be anywhere within a=> the y-posi.on has an uncertain, Δy=a.
    [Show full text]