DOCSLIB.ORG

An Introduction to Quantum Computing and Quantum Random Number Generators

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
An Introduction to Quantum Computing and Quantum Random Number Generators An introduction to Quantum Computing and Quantum Random Number Generators Giuseppe Vallone email: [email protected] INFN and The Future of Scientific Computing - 4 May 2018 Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 2 Intro Quantum Computing QRNG Conclusions Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 3 Intro Quantum Computing QRNG Conclusions What is Quantum Information? Information Theory Quantum Mechanics , Merging two big XXth century revolutions: information theory (Shannon, Turing) and Quantum Mechanics. Pag. 4 Intro Quantum Computing QRNG Conclusions Examples of applications Quantum computer Quantum cryptography Quantum metrology Pag. 5 Intro Quantum Computing QRNG Conclusions Examples of applications Quantum sensing Quantum imaging Quantum random number Quantum simulation generation Pag. 6 Intro Quantum Computing QRNG Conclusions But... ...be aware of fake! Pag. 7 Intro Quantum Computing QRNG Conclusions Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 8 Intro Quantum Computing QRNG Conclusions Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 9 Intro Quantum Computing QRNG Conclusions One-slide review of classical computation Input Output n bits m bits Universal gates: any function f : f0; 1gn ! f0; 1gm can be built from two elementary gates: NAND and COPY. Pag. 10 I Superposition principle: if j 1i and j 2i are physical states, any linear combination is a physical state: jΨi = aj 1i + bj 2i a; b 2 C I From classical bit (two orthogonal states j0i and j1i) to quantum-bit , or qubit: 2 2 j i = αj0i + βj1i α; β 2 C ; jαj + jβj = 1 Intro Quantum Computing QRNG Conclusions Quantum computer: superposition principle I Quantum mechanics: physical states are represented as vectors j i Pag. 11 I From classical bit (two orthogonal states j0i and j1i) to quantum-bit , or qubit: 2 2 j i = αj0i + βj1i α; β 2 C ; jαj + jβj = 1 Intro Quantum Computing QRNG Conclusions Quantum computer: superposition principle I Quantum mechanics: physical states are represented as vectors j i I Superposition principle: if j 1i and j 2i are physical states, any linear combination is a physical state: jΨi = aj 1i + bj 2i a; b 2 C Pag. 11 Intro Quantum Computing QRNG Conclusions Quantum computer: superposition principle I Quantum mechanics: physical states are represented as vectors j i I Superposition principle: if j 1i and j 2i are physical states, any linear combination is a physical state: jΨi = aj 1i + bj 2i a; b 2 C I From classical bit (two orthogonal states j0i and j1i) to quantum-bit , or qubit: 2 2 j i = αj0i + βj1i α; β 2 C ; jαj + jβj = 1 Pag. 11 Intro Quantum Computing QRNG Conclusions State superposition above 10000 AMU, 810 atoms Matter–wave interference of particles selected from a molecular library with masses exceeding 10000 amu, Phys. Chem. Chem. Phys. 15, 14696 (2013) Pag. 12 I Manipulate the state into jΨouti = UjΨini. U is the algorithm I Measure each qubit (usually in the computational basis) Intro Quantum Computing QRNG Conclusions Circuit model of quantum computation 0 1 Input 0 1 Output n n bits qubits 0 1 I Prepare the system into jΨini = j 0i ⊗ j 0i ⊗ · · · ⊗ j n−1i Pag. 13 I Measure each qubit (usually in the computational basis) Intro Quantum Computing QRNG Conclusions Circuit model of quantum computation 0 1 Input 0 1 Output n n bits qubits 0 1 I Prepare the system into jΨini = j 0i ⊗ j 0i ⊗ · · · ⊗ j n−1i I Manipulate the state into jΨouti = UjΨini. U is the algorithm Pag. 13 Intro Quantum Computing QRNG Conclusions Circuit model of quantum computation 0 1 Input 0 1 Output n n bits qubits 0 1 I Prepare the system into jΨini = j 0i ⊗ j 0i ⊗ · · · ⊗ j n−1i I Manipulate the state into jΨouti = UjΨini. U is the algorithm I Measure each qubit (usually in the computational basis) Pag. 13 Intro Quantum Computing QRNG Conclusions Universal gates Any quantum algorithm U can be built by the following universal gates: Hadamard Single qubit rotation CNOT gate ' 1 1 i σz 0 1 H = p1 Rz(') = e 2 1 0 0 0 2 1 −1 i ' ! B0 1 0 0C e 2 0 B C = −i ' @0 0 0 1A 0 e 2 0 0 1 0 Pag. 14 Intro Quantum Computing QRNG Conclusions Shor algorithm Problem 1: factoring Given an integer number N, find its prime factors. n1=3(log n)2=3 The best classical algorithm requires O(e 2 ) with n = log2N Problem 2: order finding Choose a generic a such that 1 < a < N. The order r of a modulo N is the minimum positive integer r such that ar = 1 mod N. Hard (probably superpolinomial) problem. Equivalence By using O(n3) classical operations Problem 1 can be reformulated as Problem 2 Pag. 15 Intro Quantum Computing QRNG Conclusions Shor algorithm Order-finding by quantum computer x Va : jxijyi ! jxijy ⊕ a mod Ni 3 I The Va operation requires O(n ) gates 2 I DFT requires O(n ) gates Pag. 16 Intro Quantum Computing QRNG Conclusions Grover algorithm problem: find x0 given a quantum black box U! such that ( −|xi for x = x0 U!jxi = jxi for x 6= x0 p x0 is found with high probability using O( N) evaluations A classical computer cannot solve the problem with less than O(N) operations Pag. 17 Intro Quantum Computing QRNG Conclusions Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 18 Intro Quantum Computing QRNG Conclusions One-way quantum computer G. Vallone, et al., One-way quantum computation with two-photon multiqubit cluster states, Phys. Rev. A 78, 042335 (2008) Pag. 19 Intro Quantum Computing QRNG Conclusions Quantum simulation Quantum Simulation, Rev. Mod. Phys. 86, 154 (2014) Pag. 20 Intro Quantum Computing QRNG Conclusions Adiabatic Quantum Computing H(t) = (1 − t)H0 + tHP 1 T = O( 2 ) gmin Adiabatic Quantum Computing, Rev. Mod. Phys. 90, 015002 (2018) Pag. 21 Intro Quantum Computing QRNG Conclusions Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 22 Intro Quantum Computing QRNG Conclusions Photons Reprogrammable optical circuit that implements all possible linear optical protocols up to the size of the circuit (six photon input) Universal linear optics, Science 349, 711 (2017) Pag. 23 Intro Quantum Computing QRNG Conclusions Trapped ion Quantum computers,Nature 464, 45 (2010) Pag. 24 Intro Quantum Computing QRNG Conclusions Ultracol atoms in lattice Quantum simulations with ultracold atoms in optical lattices, Science 357, 995 (2017) Pag. 25 Intro Quantum Computing QRNG Conclusions Nuclear Magnetic Resonance (NMR) NMR techniques for quantum control and computation, Rev. Mod. Phys. 76, 1037 (2005) Pag. 26 Intro Quantum Computing QRNG Conclusions Quantum dots Quantum computers, Nature 464, 45 (2010) Pag. 27 Intro Quantum Computing QRNG Conclusions Superconducting qubits Quantum computers, Nature 464, 45 (2010) Pag. 28 Intro Quantum Computing QRNG Conclusions D-wave Quantum annealing: finding the global minimum of a given function by using quantum fluctuations. Pag. 29 Intro Quantum Computing QRNG Conclusions Google Superconducting qubit processor A blueprint for demonstrating quantum supremacy with superconducting qubits, [arXiv: 1709.06678] Pag. 30 Intro Quantum Computing QRNG Conclusions IBM IBM’s quantum processors made up of superconducting transmon qubits https://quantumexperience.ng.bluemix.net/qx/qasm Pag. 31 Intro Quantum Computing QRNG Conclusions Microsoft “Our approach focuses on topological quantum computing through Majorana fermions, which promise to yield fast, stable quantum bits, also known as qubits.” https://www.microsoft.com/en-us/quantum/technology Pag. 32 Intro Quantum Computing QRNG Conclusions Summary 1 Introduction 2 Quantum Computing Circuit model Alternatives to circuit model Implementations 3 Quantum Random Number Generators 4 Conclusions Pag. 33 Intro Quantum Computing QRNG Conclusions What is a random number A random number is a number generated by an unpredictable process Pag. 34 Intro Quantum Computing QRNG Conclusions Why random numbers? Random numbers are crucial in several applications: 1 Information technology and security (also QKD) 2 Scientific simulation (meteorology, biology, physics...) 3 Lottery/gaming Pag. 35 Head or tail? How random is it? Intro Quantum Computing QRNG Conclusions Generators based on classical physics How we generate random numbers? Pag. 36 Intro Quantum Computing QRNG Conclusions Generators based on classical physics How we generate random numbers? Head or tail? How random is it? Pag. 36 Intro Quantum Computing QRNG Conclusions Generators based on classical physics Output depends deterministically from initial conditions Pag. 37 Intro Quantum Computing QRNG Conclusions Pseudo Random Number Generators Pseudo-random numbers are generated by a deterministic algorithm that produces a sequence that “resemble” a random sequence PROS CONS I simple I period I fast I not-uniformity I correlations Pag. 38 Intro Quantum Computing QRNG Conclusions but.... Von Neumann (1903-1957) (among the father of information theory "Anyone who attempts to generate random numbers by deterministic means is, of course, living in a state of sin" Pag. 39 Intro Quantum Computing QRNG Conclusions Problems of PRNG V1 12589822 V2 490623226 RANDU V3 682947310 V4 1829558474 used by IBM from ’60 to ’90 V5 535857758 V6 1781505818 31 V7 1571347790 Vk+1 = 65539 · Vk mod 2 V8 1984468970 V9 2059651006 V10 940136250 Pag. 40 Intro Quantum Computing QRNG Conclusions Problems of PRNG V1 12589822 V2 490623226 RANDU V3 682947310 V4 1829558474 used by IBM from ’60 to ’90 V5 535857758 V6 1781505818 31 V7 1571347790 Vk+1 = 65539 · Vk mod 2 V8 1984468970 V9 2059651006 V10 940136250 Pag.
Load more

Recommended publications
  • 31 Diffraction and Interference.Pdf
    Diffraction and Interference Figu These expar new .5 wave oday Isaac Newton is most famous for his new v accomplishments in mechanics—his laws of Tmotion and universal gravitation. Early in his career, however, he was most famous for his work on light. Newton pictured light as a beam of ultra-tiny material particles. With this model he could explain reflection as a bouncing of the parti- cles from a surface, and he could explain refraction as the result of deflecting forces from the surface Interference colors. acting on the light particles. In the eighteenth and nineteenth cen- turies, this particle model gave way to a wave model of light because waves could explain not only reflection and refraction, but everything else that was known about light at that time. In this chapter we will investigate the wave aspects of light, which are needed to explain two important phenomena—diffraction and interference. As Huygens' Principle origin; 31.1 pie is I constr In the late 1600s a Dutch mathematician-scientist, Christian Huygens, dimen proposed a very interesting idea about waves. Huygens stated that light waves spreading out from a point source may be regarded as die overlapping of tiny secondary wavelets, and that every point on ' any wave front may be regarded as a new point source of secondary waves. We see this in Figure 31.1. In other words, wave fronts are A made up of tinier wave fronts. This idea is called Huygens' principle. Look at the spherical wave front in Figure 31.2. Each point along the wave front AN is the source of a new wavelet that spreads out in a sphere from that point.
    [Show full text]
  • Schrödinger Equation)
    Lecture 37 (Schrödinger Equation) Physics 2310-01 Spring 2020 Douglas Fields Reduced Mass • OK, so the Bohr model of the atom gives energy levels: • But, this has one problem – it was developed assuming the acceleration of the electron was given as an object revolving around a fixed point. • In fact, the proton is also free to move. • The acceleration of the electron must then take this into account. • Since we know from Newton’s third law that: • If we want to relate the real acceleration of the electron to the force on the electron, we have to take into account the motion of the proton too. Reduced Mass • So, the relative acceleration of the electron to the proton is just: • Then, the force relation becomes: • And the energy levels become: Reduced Mass • The reduced mass is close to the electron mass, but the 0.0054% difference is measurable in hydrogen and important in the energy levels of muonium (a hydrogen atom with a muon instead of an electron) since the muon mass is 200 times heavier than the electron. • Or, in general: Hydrogen-like atoms • For single electron atoms with more than one proton in the nucleus, we can use the Bohr energy levels with a minor change: e4 → Z2e4. • For instance, for He+ , Uncertainty Revisited • Let’s go back to the wave function for a travelling plane wave: • Notice that we derived an uncertainty relationship between k and x that ended being an uncertainty relation between p and x (since p=ћk): Uncertainty Revisited • Well it turns out that the same relation holds for ω and t, and therefore for E and t: • We see this playing an important role in the lifetime of excited states.
    [Show full text]
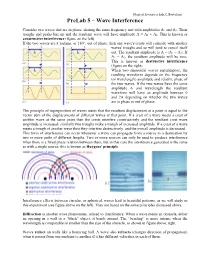
  • Prelab 5 – Wave Interference
    Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths.
    [Show full text]
  • Lecture 9, P 1 Lecture 9: Introduction to QM: Review and Examples
    Lecture 9, p 1 Lecture 9: Introduction to QM: Review and Examples S1 S2 Lecture 9, p 2 Photoelectric Effect Binding KE=⋅ eV = hf −Φ energy max stop Φ The work function: 3.5 Φ is the minimum energy needed to strip 3 an electron from the metal. 2.5 2 (v) Φ is defined as positive . 1.5 stop 1 Not all electrons will leave with the maximum V f0 kinetic energy (due to losses). 0.5 0 0 5 10 15 Conclusions: f (x10 14 Hz) • Light arrives in “packets” of energy (photons ). • Ephoton = hf • Increasing the intensity increases # photons, not the photon energy. Each photon ejects (at most) one electron from the metal. Recall: For EM waves, frequency and wavelength are related by f = c/ λ. Therefore: Ephoton = hc/ λ = 1240 eV-nm/ λ Lecture 9, p 3 Photoelectric Effect Example 1. When light of wavelength λ = 400 nm shines on lithium, the stopping voltage of the electrons is Vstop = 0.21 V . What is the work function of lithium? Lecture 9, p 4 Photoelectric Effect: Solution 1. When light of wavelength λ = 400 nm shines on lithium, the stopping voltage of the electrons is Vstop = 0.21 V . What is the work function of lithium? Φ = hf - eV stop Instead of hf, use hc/ λ: 1240/400 = 3.1 eV = 3.1eV - 0.21eV For Vstop = 0.21 V, eV stop = 0.21 eV = 2.89 eV Lecture 9, p 5 Act 1 3 1. If the workfunction of the material increased, (v) 2 how would the graph change? stop a.
    [Show full text]
  • Waves: Interference Instructions: Read Through the Information Below
    Pre-AP Physics Week 2: Day 1 Notes Waves: Interference Instructions: Read through the information below. Then answer the questions below. When two or more waves meet, they interact with each other. The interaction of waves with other waves is called wave interference. Wave interference may occur when two waves that are traveling in opposite directions meet. The two waves pass through each other, and this affects their amplitude. Amplitude is the maximum distance the particles of the medium move from their resting positions when a wave passes through. How amplitude is affected by wave interference depends on the type of interference. Interference can be constructive or destructive. Constructive Interference Destructive Interference Constructive interference occurs when crests of one Destructive interference occurs when the crests of one wave overlap the crests of the other wave. The figure wave overlap the troughs, or lowest points, of another above shows what happens. As the waves pass through wave. The figure above shows what happens. As the each other, the crests combine to produce a wave with waves pass through each other, the crests and troughs greater amplitude. The same can happen with two cancel each other out to produce a wave with zero troughs interacting. amplitude. (NOTE: They don’t always have to fully cancel out. Destructive interference can be partial cancellation.) TRUE or FALSE: Identify the following statements as being either true (T) or false (F). 1. When two pulses meet up with each other while moving through the same medium, they tend to bounce off each other and return back to their origin.
    [Show full text]
  • Time-Domain Grating with a Periodically Driven Qutrit
    PHYSICAL REVIEW APPLIED 11, 014053 (2019) Time-Domain Grating with a Periodically Driven Qutrit Yingying Han,1,2,3,§ Xiao-Qing Luo,2,3,§ Tie-Fu Li,4,2,* Wenxian Zhang,1,† Shuai-Peng Wang,2 J.S. Tsai,5,6 Franco Nori,5,7 and J.Q. You3,2,‡ 1 School of Physics and Technology, Wuhan University, Wuhan, Hubei 430072, China 2 Quantum Physics and Quantum Information Division, Beijing Computational Science Research Center, Beijing 100193, China 3 Interdisciplinary Center of Quantum Information and Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics and State Key Laboratory of Modern Optical Instrumentation, Zhejiang University, Hangzhou 310027, China 4 Institute of Microelectronics, Department of Microelectronics and Nanoelectronics, and Tsinghua National Laboratory of Information Science and Technology, Tsinghua University, Beijing 100084, China 5 Theoretical Quantum Physics Laboratory, RIKEN Cluster for Pioneering Research, Wako-shi, Saitama 351-0198, Japan 6 Department of Physic, Tokyo University of Science, Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan 7 Department of Physics, The University of Michigan, Ann Arbor, Michigan 48109-1040, USA (Received 23 October 2018; revised manuscript received 3 December 2018; published 28 January 2019) Physical systems in the time domain may exhibit analogous phenomena in real space, such as time crystals, time-domain Fresnel lenses, and modulational interference in a qubit. Here, we report the experi- mental realization of time-domain grating using a superconducting qutrit in periodically modulated probe and control fields via two schemes: simultaneous modulation and complementary modulation. Both exper- imental and numerical results exhibit modulated Autler-Townes (AT) and modulation-induced diffraction (MID) effects.
    [Show full text]
  • Physical Quantum States and the Meaning of Probability Michel Paty
    Physical quantum states and the meaning of probability Michel Paty To cite this version: Michel Paty. Physical quantum states and the meaning of probability. Galavotti, Maria Carla, Suppes, Patrick and Costantini, Domenico. Stochastic Causality, CSLI Publications (Center for Studies on Language and Information), Stanford (Ca, USA), p. 235-255, 2001. halshs-00187887 HAL Id: halshs-00187887 https://halshs.archives-ouvertes.fr/halshs-00187887 Submitted on 15 Nov 2007 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. as Chapter 14, in Galavotti, Maria Carla, Suppes, Patrick and Costantini, Domenico, (eds.), Stochastic Causality, CSLI Publications (Center for Studies on Language and Information), Stanford (Ca, USA), 2001, p. 235-255. Physical quantum states and the meaning of probability* Michel Paty Ëquipe REHSEIS (UMR 7596), CNRS & Université Paris 7-Denis Diderot, 37 rue Jacob, F-75006 Paris, France. E-mail : [email protected] Abstract. We investigate epistemologically the meaning of probability as implied in quantum physics in connection with a proposed direct interpretation of the state function and of the related quantum theoretical quantities in terms of physical systems having physical properties, through an extension of meaning of the notion of physical quantity to complex mathematical expressions not reductible to simple numerical values.
    [Show full text]
  • Uniting the Wave and the Particle in Quantum Mechanics
    Uniting the wave and the particle in quantum mechanics Peter Holland1 (final version published in Quantum Stud.: Math. Found., 5th October 2019) Abstract We present a unified field theory of wave and particle in quantum mechanics. This emerges from an investigation of three weaknesses in the de Broglie-Bohm theory: its reliance on the quantum probability formula to justify the particle guidance equation; its insouciance regarding the absence of reciprocal action of the particle on the guiding wavefunction; and its lack of a unified model to represent its inseparable components. Following the author’s previous work, these problems are examined within an analytical framework by requiring that the wave-particle composite exhibits no observable differences with a quantum system. This scheme is implemented by appealing to symmetries (global gauge and spacetime translations) and imposing equality of the corresponding conserved Noether densities (matter, energy and momentum) with their Schrödinger counterparts. In conjunction with the condition of time reversal covariance this implies the de Broglie-Bohm law for the particle where the quantum potential mediates the wave-particle interaction (we also show how the time reversal assumption may be replaced by a statistical condition). The method clarifies the nature of the composite’s mass, and its energy and momentum conservation laws. Our principal result is the unification of the Schrödinger equation and the de Broglie-Bohm law in a single inhomogeneous equation whose solution amalgamates the wavefunction and a singular soliton model of the particle in a unified spacetime field. The wavefunction suffers no reaction from the particle since it is the homogeneous part of the unified field to whose source the particle contributes via the quantum potential.
    [Show full text]
  • 1 the Principle of Wave–Particle Duality: an Overview
    3 1 The Principle of Wave–Particle Duality: An Overview 1.1 Introduction In the year 1900, physics entered a period of deep crisis as a number of peculiar phenomena, for which no classical explanation was possible, began to appear one after the other, starting with the famous problem of blackbody radiation. By 1923, when the “dust had settled,” it became apparent that these peculiarities had a common explanation. They revealed a novel fundamental principle of nature that wascompletelyatoddswiththeframeworkofclassicalphysics:thecelebrated principle of wave–particle duality, which can be phrased as follows. The principle of wave–particle duality: All physical entities have a dual character; they are waves and particles at the same time. Everything we used to regard as being exclusively a wave has, at the same time, a corpuscular character, while everything we thought of as strictly a particle behaves also as a wave. The relations between these two classically irreconcilable points of view—particle versus wave—are , h, E = hf p = (1.1) or, equivalently, E h f = ,= . (1.2) h p In expressions (1.1) we start off with what we traditionally considered to be solely a wave—an electromagnetic (EM) wave, for example—and we associate its wave characteristics f and (frequency and wavelength) with the corpuscular charac- teristics E and p (energy and momentum) of the corresponding particle. Conversely, in expressions (1.2), we begin with what we once regarded as purely a particle—say, an electron—and we associate its corpuscular characteristics E and p with the wave characteristics f and of the corresponding wave.
    [Show full text]
  • Path Integral Quantum Monte Carlo Study of Coupling and Proximity Effects in Superfluid Helium-4
    Path Integral Quantum Monte Carlo Study of Coupling and Proximity Effects in Superfluid Helium-4 A Thesis Presented by Max T. Graves to The Faculty of the Graduate College of The University of Vermont In Partial Fullfillment of the Requirements for the Degree of Master of Science Specializing in Materials Science October, 2014 Accepted by the Faculty of the Graduate College, The University of Vermont, in partial fulfillment of the requirements for the degree of Master of Science in Materials Science. Thesis Examination Committee: Advisor Adrian Del Maestro, Ph.D. Valeri Kotov, Ph.D. Frederic Sansoz, Ph.D. Chairperson Chris Danforth, Ph.D. Dean, Graduate College Cynthia J. Forehand, Ph.D. Date: August 29, 2014 Abstract When bulk helium-4 is cooled below T = 2.18 K, it undergoes a phase transition to a su- perfluid, characterized by a complex wave function with a macroscopic phase and exhibits inviscid, quantized flow. The macroscopic phase coherence can be probed in a container filled with helium-4, by reducing one or more of its dimensions until they are smaller than the coherence length, the spatial distance over which order propagates. As this dimensional reduction occurs, enhanced thermal and quantum fluctuations push the transition to the su- perfluid state to lower temperatures. However, this trend can be countered via the proximity effect, where a bulk 3-dimensional (3d) superfluid is coupled to a low (2d) dimensional su- perfluid via a weak link producing superfluid correlations in the film at temperatures above the Kosterlitz-Thouless temperature. Recent experiments probing the coupling between 3d and 2d superfluid helium-4 have uncovered an anomalously large proximity effect, leading to an enhanced superfluid density that cannot be explained using the correlation length alone.
    [Show full text]
  • Matter-Wave Diffraction of Quantum Magical Helium Clusters Oleg Kornilov * and J
    s e r u t a e f Matter-wave diffraction of quantum magical helium clusters Oleg Kornilov * and J. Peter Toennies , Max-Planck-Institut für Dynamik und Selbstorganisation, Bunsenstraße 10 • D-37073 Göttingen • Germany. * Present address: Chemical Sciences Division, Lawrence Berkeley National Lab., University of California • Berkeley, CA 94720 • USA. DOI: 10.1051/epn:2007003 ack in 1868 the element helium was discovered in and named Finally, helium clusters are the only clusters which are defi - Bafter the sun (Gr.“helios”), an extremely hot environment with nitely liquid. This property led to the development of a new temperatures of millions of degrees. Ironically today helium has experimental technique of inserting foreign molecules into large become one of the prime objects of condensed matter research at helium clusters, which serve as ultra-cold nano-containers. The temperatures down to 10 -6 Kelvin. With its two very tightly bound virtually unhindered rotations of the trapped molecules as indi - electrons in a 1S shell it is virtually inaccessible to lasers and does cated by their sharp clearly resolved spectral lines in the infrared not have any chemistry. It is the only substance which remains liq - has been shown to be a new microscopic manifestation of super - uid down to 0 Kelvin. Moreover, owing to its light weight and very fluidity [3], thus linking cluster properties back to the bulk weak van der Waals interaction, helium is the only liquid to exhib - behavior of liquid helium. it one of the most striking macroscopic quantum effects: Today one of the aims of modern helium cluster research is to superfluidity.
    [Show full text]
  • When the Uncertainty Principle Goes to 11... Or How to Explain Quantum Physics with Heavy Metal
    Ronald E. Hatcher Science on Saturday Lecture Series 12 January 2019 When The Uncertainty Principle goes to 11... or How to Explain Quantum Physics with Heavy Metal Philip Moriarty Professor, University of Nottingham, United Kingdom ABSTRACT: There are deep and fundamental linKs between quantum physics and heavy metal. No, really. There are. Far from being music for Neanderthals, as it’s too often construed, metal can be harmonically and rhythmically complex. That complexity is the source of many connections to the quantum world. You’ll discover how the Heisenberg uncertainty principle comes into play with every chugging guitar riff, what wave interference has to do with Iron Maiden, and why metalheads in mosh pits behave just liKe molecules in a gas. BIOGRAPHY: Philip Moriarty is a professor of physics, a heavy metal fan, a Keen air-drummer, and author of “When The Uncertainty Principle Goes To 11 (or How To Explain Quantum Physics With Heavy Metal” (Ben Bella 2018). His research at the University of Nottingham focuses on prodding, pushing, and poKing single atoms and molecules; in this nanoscopic world, quantum physics is all. Moriarty has taught physics for twenty years and has always been strucK by the number of students in his classes who profess a love of metal music, and by the deep connections between heavy metal and quantum mechanics. A frequent contributor to the Sixty Symbols YouTube channel, which won the Institute of Physics’ Kelvin Award in 2016 for “for innovative and effective promotion of the public understanding of physics”, he has a Keen interest in public engagement, outreach, and bridging the arts-science divide.
    [Show full text]