DOCSLIB.ORG

Perspectives in Quantum Physics: Epistemological, Ontological And

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Perspectives in Quantum Physics: Epistemological, Ontological And !"#$%"&'()"$*(+*,-.+'-/*!01$(&$2* 3%($'"/4546(&.57*8+'4546(&.5*.+9* !"9.646(&.5* * :+*(+)"$'(6.'(4+*(+'4*$'-9"+'*.+9*";%"#'* %"#$%"&'()"$*4+*'0"*%01$(&.5*(+'"#%#"'.'(4+*4<* =-.+'-/*/"&0.+(&$7*>('0*(/%5(&.'(4+$*<4#*/49"#+* %01$(&$*(+$'#-&'(4+?* * * * !"#$%&'()#*+,-.(/#0%*( ( /1(2344567(89(2:;;:6(<-0=&$'0>*(,?(!,%,$#.,(#>(/,@%.&$( ( ( 1(>"&'0'('@A+0>>&.(>,(>"&( B#C@%>*(,?(>"&(D$#.@#>&(9C",,%(,?(>"&( <-0=&$'0>*(,?(!,%,$#.,(0-(E#$>0#%(?@%?0%%+&->( ,?(>"&($&F@0$&+&->'(?,$(>"&(.&G$&&(,?( H,C>,$(,?(I"0%,',E"*( H&E#$>+&->(,?(I"*'0C'( :;33( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( J"0'(>"&'0'(&->0>%&.( ( I&$'E&C>0=&'(0-(K@#->@+(I"*'0C'L( ME0'>&+,%,G0C#%7(N->,%,G0C#%(#-.(I&.#G,G0C#%( ( O$0>>&-(A*(!"#$%&'()#*+,-.(/#0%*( ( "#'(A&&-(#EE$,=&.(A*(>"&(H&E#$>+&->(,?(I"*'0C'( ( ( ( ( ( PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP( ( 2Q,#"(B0-R&%'>&0-6( ( ( ( PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP( ( 280C"#&%(H@A',-6( ( ( ( PPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPPP( ( 25S:S:;336( ( ( J"&(?0-#%(C,E*(,?(>"0'(>"&'0'("#'(A&&-(&T#+0-&.(A*(>"&('0G-#>,$0&'7(#-.( O&(?0-.(>"#>(A,>"(>"&(C,->&->(#-.(?,$+(+&&>(#CC&E>#A%&(E$&'&->#>0,-( '>#-.#$.'(,?('C",%#$%*(O,$R(0-(>"&(#A,=&(+&->0,-&.(.0'C0E%0-&U( V)!(I$,>,C,%(W(;:;5U:3( ( ( ( ( ( ( ( ABSTRACT /#0%*7(!"#$%&'()#*+,-.(2I"UH7(I"*'0C'6( J0>%&L(I&$'E&C>0=&'(0-(K@#->@+(I"*'0C'L(ME0'>&+,%,G0C#%7(N->,%,G0C#%(#-.(I&.#G,G0C#%( J"&'0'(.0$&C>&.(A*(1'',C0#>&(I$,?&'',$(Q,#"(HU(B0-R&%'>&0-( ( ( 1( C,++,-( %&#$-0-G( G,#%( ?,$( +,.&$-( E"*'0C'( 0-'>$@C>,$'( 0'( ?,$( '>@.&->'( >,( $&C,G-0X&( #( .0??&$&-C&( A&>O&&-( >"&( &TE&$0+&->#%( @-C&$>#0->*( ,?( C%#''0C#%( E"*'0C'( #-.( >"&( ?@-.#+&->#%( @-C&$>#0->*( ,?( F@#->@+( +&C"#-0C'U( ( N@$( '>@.0&'( '@GG&'>( >"0'( -,>,$0,@'%*( .0??0C@%>( >#'R( +#*( A&( ?$@'>$#>&.( A*( >"&( 0->@0>0=&%*( !"#$%&'(E&$'E&C>0=&'(,?( 0->$,.@C>,$*('>@.&->'7(#-.(#(%#CR(,?(()'($(*%+#$,-$".%/%$%'0(0-(>"&0$(C,-C&E>0,-'(,?(%0G">( #-.( +#>>&$U((Y&("#=&(.&=&%,E&.(#(?$#+&O,$R(?,$(@-.&$'>#-.0-G(#-.(C"#$#C>&$0X0-G( '>@.&->( E&$'E&C>0=&'( ,-( >"&( E"*'0C#%( 0->&$E$&>#>0,-( ,?( F@#->@+( +&C"#-0C'7( #-.( .&+,-'>$#>&(>"&(.0??&$&->0#%(0+E#C>(,-('>@.&->(>"0-R0-G(,?(>"&(+*$0#.(O#*'(0-'>$@C>,$'( #EE$,#C"( 0->&$E$&>0=&( >"&+&'( 0-( >"&0$( 0->$,.@C>,$*( C,@$'&'U( ( Z0R&( &TE&$>( E"*'0C0'>'7( '>@.&->'( 0->&$E$&>( F@#->@+( E"&-,+&-#( .0??&$&->%*7( #-.( >"&'&( 0->&$E$&>#>0,-'( #$&( '0G-0?0C#->%*( 0-?%@&-C&.( A*( >"&0$( ,=&$#%%( '>#-C&'( ,-( F@&'>0,-'( C&->$#%( >,( >"&( ',[C#%%&.( 1"#&2!"1")',3!(/$"1L( \'( >"&(O#=&(?@-C>0,-(E"*'0C#%%*($&#%7(,$('0+E%*(#(+#>"&+#>0C#%( >,,%]( ( \'( >"&( +($$#3&", (-, '4", 5#6", -2)+'%()(#-(#7, 4(+($@%&7(,$(#(E"*'0C#%(>$#-'0>0,-(-,>( .&'C$0A&.(A*(#-*(&F@#>0,-]((H,&'(#-(&%&C>$,-7(A&0-G(#(?,$+(,?(+#>>&$7(&T0'>(#'(#(%,C#%0X&.( E#$>0C%&(#>(#%%(>0+&']((J"&'&(F@&'>0,-'7(O"0C"(#$&(,?(E&$',-#%(#-.(#C#.&+0C(0->&$&'>(>,( ,@$('>@.&->'7(#$&(%#$G&%*(,-%*('@E&$?0C0#%%*(#..$&''&.(0-(,@$(0->$,.@C>,$*(C,@$'&'7(,?>&-( ?,$( ?&#$( ,?( ,E&-0-G( #( 8#)7(!#9&, :(.(,?('>@.&->(F@&'>0,-'7(-,-&(,?(O"0C"("#=&(&#'*( #-'O&$'U( ( Y&( '",O( ",O( #( >$#-'?,$+&.( +,.&$-( E"*'0C'( C@$$0C@%@+( 2$&C&->%*( 0+E%&+&->&.(#>(>"&(<-0=&$'0>*(,?(!,%,$#.,6(+#*(E,'0>0=&%*(0+E#C>('>@.&->(E&$'E&C>0=&'( ,-( 0-.&>&$+0-#C*( #-.( O#=&[E#$>0C%&( .@#%0>*7( A*( +#R0-G( F@&'>0,-'( ,?( C%#''0C#%( #-.( F@#->@+( $&#%0>*( #( C&->$#%( >"&+&( ,?( ,@$( C,@$'&7( A@>( #%',( A*( +#R0-G( >"&( A&%0&?'( ,?( ,@$( '>@.&->'7(#-.(-,>(^@'>(>",'&(,?('C0&->0'>'7(#-(&TE%0C0>(>,E0C(,?(.0'C@''0,-U( ACKNOWLEDGEMENTS J"0'( O,$R( "#'( A&&-( '@EE,$>&.( 0-( E#$>( A*( Q9B( !1)MM)( D$#->( Q,U( ;__`3ab( #-.( >"&( <-0=&$'0>*(,?(!,%,$#.,U( ( \( O0'"( >,( &TE$&''( +*( +,'>( '0-C&$&( #-.( @-&-.0-G( G$#>0>@.&( ?,$( >"&( C,,E&$#>0,-( ,?( #%%( >"&( +,.&$-( E"*'0C'( 0-'>$@C>,$'( #-.( '>@.&->'( O",(+#.&(>"&'&('>@.0&'(E,''0A%&7(A@>(E#$>0C@%#$%*(,@$(,O-('>@.&->'(?$,+(>"&(B#%%( :;3;( '&+&'>&$7( O",( O&$&( 0-=,%@->#$*( A@>( &->"@'0#'>0C( E#$>0C0E#->'( 0-( >"0'( .0''&$>#>0,-(E$,^&C>U((\(#+(#%',(0-.&A>&.(>,(#%%(>"&(+&+A&$'(,?(>"&(I"*'0C'(M.@C#>0,-( )&'&#$C"(G$,@E(#>(!<7(?,$(>"&0$(C,->0-@&.(0-'0G">(#-.(0->&$&'>(,=&$(>"&('E#-(,?(?,@$( *&#$'U((8,'>(0+E,$>#->%*7(\(#+(G$#>&?@%(?,$(>"&(&-.@$0-G('@EE,$>(,?(+*(#.=0',$(#-.( +&->,$7(Q,#"(B0-R&%'>&0-U(( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( ( TABLE OF CONTENTS @0.%'"#*A2*!"#$%"&'()"$*(+*,-.+'-/*!01$(&$* * * * A* ( \U \->$,.@C>0,-( ( ( ( ( ( ( ( 3( 1U Q,>0,-'(,?(!%#''0C#%(#-.(K@#->@+()&#%0>*( ( ( 3( /U I"0%,',E"*(,$(9C0&-C&]( ( ( ( ( _( !U Y#=&[I#$>0C%&(H@#%0>*(#-.(N->,%,G0C#%(B%&T0A0%0>*(( a( ( \\U ME0'>&+,%,G*(#-.(N->,%,G*(0-(I"*'0C'(\-'>$@C>0,-( ( 3a( ( \\\U 8,>0=#>0,-(#-.(N=&$=0&O(,?(H0''&$>#>0,-(I$,^&C>(( ( :;( ( )&?&$&-C&'(2!"#E>&$(36( ( ( ( ( ( ( :4( * @0.%'"#*B2*C")"54%/"+'*4<*D'-9"+'*!"#$%"&'()"$*E*F+('(.5*D'-9("$* GH* ( \U \->$,.@C>0,-( ( ( ( ( ( ( ( ca( ( \\U 9>@.0&'( ( ( ( ( ( ( ( ( ca( 1U 9>@.&->(0.&#'(#A,@>(+&#'@$&+&->(C"#-G&(,=&$(>0+&( c`( /U \-'>$@C>0,-#%(C",0C&'(0-?%@&-C&('>@.&->(E&$'E&C>0=&'( _3( !U !,-'0'>&-C*(,?('>@.&->(E&$'E&C>0=&'( ( ( _5( ( \\\U 9@++#$*(#-.(H0'C@''0,-( ( ( ( ( ( _b( ( )&?&$&-C&'(2!"#E>&$(:6( ( ( ( ( ( ( _`( * @0.%'"#*G2*,-.+'-/*F+'"#%#"'.'(4+*.$*I(99"+*@-##(&-5-/*E** J.#(.'(4+$*(+*F+$'#-&'4#*!#.&'(&"$*.+9*:$$4&(.'"9** D'-9"+'*8-'&4/"$* * * * * 53* ( \U \->$,.@C>0,-( ( ( ( ( ( ( ( 53( ( \\U \-'>$@C>,$'(#EE$,#C"(F@#->@+(0->&$E$&>#>0,-(.0??&$&->%*( 5c( ( \\\U !,+E#$0-G(\-'>$@C>,$(I$#C>0C&'(21(!%,'&$(Z,,R6( ( ( 5b( 1U /#CRG$,@-.(,-(C,@$'&(+#>&$0#%'(#-.(C@$$0C@%@+(( '0+0%#$0>0&'( ( ( ( ( ( ( 5b( ( /U H0??&$&-C&'(0-(0-'>$@C>0,-#%(#EE$,#C"&'( ( ( 5a( !U J"&(.,@A%&['%0>(&TE&$0+&->(O0>"('0-G%&(F@#->#( ( b:( HU 2\-6C,-'0'>&-C*(,?('>@.&->($&'E,-'&'( ( ( b5( ( \dU 9@++#$*(#-.(H0'C@''0,-( ( ( ( ( ( ba( ( )&?&$&-C&'(2!"#E>&$(c6( ( ( ( ( ( ( b4( ( @0.%'"#*K2*L"<(+"9*@0.#.&'"#(M.'(4+$*4<*D'-9"+'*!"#$%"&'()"$* 4+*,-.+'-/*!01$(&$* * * * * HA* ( \U \->$,.@C>0,-( ( ( ( ( ( ( ( a3( ( \\U \->&$=0&O(E#$>0C0E#->'(#-.(C,@$'&(C"#$#C>&$0'>0C'( ( a:( ( \\\U )&?0-&.(C"#$#C>&$0X#>0,-'(,?('>@.&->(E&$'E&C>0=&'( ( a_( 1U H0'C@''0,-(,?(?,$+#%(0->&$E$&>#>0,-'( ( ( a5( ( /U 9>@.&->'(&TE$&''(A&%0&?'(>"#>(E#$#%%&%(>",'&(,?(&TE&$>( E$,E,-&->'( ( ( ( ( ( ( ab( !U !#>&G,$0X#>0,-(#-.('@++#$*(,?('>@.&->($&'E,-'&'( `;( ( \dU 9@++#$*(#-.(H0'C@''0,-( ( ( ( ( ( `a( ( )&?&$&-C&'(2!"#E>&$(_6( ( ( ( ( ( ( 43( ( @0.%'"#*N2*O".&0(+6*,-.+'-/*F+'"#%#"'.'(4+$*E*@-##(&-5-/* C")"54%/"+'*.+9*F/%5"/"+'.'(4+* * * PG* ( \U \->$,.@C>0,-( ( ( ( ( ( ( ( 4c( ( \\U !@$$0C@%@+(H&=&%,E+&->(#-.(\+E%&+&->#>0,-( ( ( 4_( 1U 1''&''0-G(0-C,+0-G('>@.&->(E&$'E&C>0=&'(#-.(( C,-C&E>@#%(@-.&$'>#-.0-G( ( ( ( 44( ( /U Z&C>@$&(8#>&$0#%'( ( ( ( ( ( 3;b( !U V,+&O,$R( ( ( ( ( ( ( 3:;( HU MT#+(8#>&$0#%'(( ( ( ( ( ( 3:5( MU 1''&''0-G(,@>G,0-G(E&$'E&C>0=&'( ( ( ( 3:4( BU B0-#%(M''#*( ( ( ( ( ( ( 3cb( ( )&?&$&-C&'(2!"#E>&$(56( ( ( ( ( ( ( 3c`( ( * * @0.%'"#*Q2*O".&0(+6*,-.+'-/*F+'"#%#"'.'(4+$*E*@4/%.#.'()"* *8-'&4/"$*.+9*@-##(&-5-/*L"<(+"/"+'* * AKA* ( \U \->$,.@C>0,-( ( ( ( ( ( ( ( 3_3( ( \\U !,+E#$#>0=&(N@>C,+&'( ( ( ( ( ( 3_3( 1U 9>@.&->(\->&$&'>(0-(K@#->@+(8&C"#-0C'( ( ( 3_:( /U \->&$E$&>0=&(1>>0>@.&'(( ( ( ( ( 3__( ( \\\U !@$$0C@%@+()&?0-&+&->(#-.(N>"&$(B@>@$&(H0$&C>0,-'( ( 353( 1U 90-G%&[I",>,-(MTE&$0+&->'( ( ( ( ( 35:( /U M->#-G%&+&->(#-.(!,$$&%#>&.(8&#'@$&+&->'( ( 354( !U 1>,+0C(8,.&%'(#-.(I$,A#A0%0>*( ( ( ( 3b;( ( \dU !,-C%@.0-G()&+#$R'( ( ( ( ( ( ( 3b:( ( )&?&$&-C&'(2!"#E>&$(b6( ( ( ( ( ( ( 3b5( ( R(S5(46#.%01( ( ( ( ( ( ( ( ( AQH( * :%%"+9(&"$** ( ( ( ( ( ( ( ( ( ( 1EE&-.0T(1(e(M=,%@>0,-(,?(N-%0-&(9@$=&*(\>&+'( ( ( ( ( 1EE&-.0T(/(e(\->&$=0&O(I$,>,C,%(29E$0-G(:;;46( ( ( ( ( 1EE&-.0T(!(e(9&%&C>&.(8,.&$-(I"*'0C'(!,@$'&(8#>&$0#%'(2B#%%(:;3;6( ( 1EE&-.0T(H(e(9&%&C>&.(V,+&O,$R7(MT#+7(9@$=&*(#-.(B0-#%(M''#*( (9@A+0''0,-'(?$,+(B,@$(9>@.&->'(2B#%%(:;3;6(( ( 1EE&-.0T(M(e(!,%%&C>&.(MTC&$E>'(?$,+(9>@.&->()&?%&C>0,-'(2B#%%(:;3;6( ( 1EE&-.0T(B(e(9&%&C>&.(9>@.&->(H0'C@''0,-(J"$&#.'(2B#%%(:;3;6( ( ( ( ( ( ( ( ( ( ( ( ( ( ( !"#$%&'()( ( $*+,-*./01*,(02(3452/46($78,0.,( ( “Why do some textbooks not mention complementarity? Because it will not help in quantum mechanical calculations or in setting up experiments. Bohr’s considerations are extremely relevant, however, to the scientist who occasionally likes to reflect on the meaning of what she or he is doing.” – Abraham Pais [1] ! 9:(92/+;<4./0;2( 9:#:(=;/0;2,(;>(!?5,,0.5?(52<(3452/46('*5?0/8! ! "#$%&'!()*+'%)*!,-*+).%&%.!'/%!0)1!-2!3/4+),+!'-!$%!5'/%!,-13#%'%!.%+,&)3')-*! -2!0*4!6)*.)7).80#9!&%0#!+)'80')-*!60+!)'!+833-+%.#4!%:)+'+!)&&%+3%,')7%!-2!0*4!0,'!-2! -$+%&70')-*!-&!+8$+'0*')0')-*9;<!=>?!@)+!+'0'%1%*'!-*!'/%!!"#!$%&!-2!+,)%*,%!+3%0A+! 0#+-!-2!/)+!3&%.)+3-+)')-*!'-B0&.!'/)*A)*C!-2!'/%!8*)7%&+%!)'+%#2!)*!'%&1+!-2!#&'()%*! %:3%,'0')-*+D! '/%&%! )%!0*! -$E%,')7%!&%0#)'4!'/0'!%:)+'+! )*.%3%*.%*'! -2! 0*4! /810*! -$+%&70')-*;!!F*! -'/%&! B-&.+G!0!+$,!(&*&!.%+,&)3')-*! 6-&! '/%-&49! -2! '/0'! -$E%,')7%! &%0#)'4! )+! 1)*)10##4! ,-13&)+%.! -2! %#%1%*'+! )*! -*%H'-H-*%! ,-&&%+3-*.%*,%! B)'/! 3/4+),0#! I80*')')%+! 6+8,/! 0+! 3-+)')-*! -&! 1-1%*'819! '/0'! 0&%! 0++81%.! '-! /07%! .%2)*)'%G!-$E%,')7%#4!&%0#!70#8%+!0'!0##!')1%+;!=J?! ! K8,/!0++813')-*+!0$-8'!'/%!*0'8&%!-2!&%0#)'4!0&%!$8)#'!)*'-!'/%!%I80')-*+!-2! ,#0++),0#! 1%,/0*),+! L!)*!.%+,&)$)*C!'/%!3-+)')-*!-2!0!2&%%!%#%,'&-*!B)'/!0!C)7%*! 1-1%*'81! 0'! +-1%! #0'%&! ')1%G! )'! )+! 0#&%0.4! 0++81%.! '/%! %#%,'&-*! B0+! )*)')0##4! #-,0'%.!0'!+-1%!.%2)*)'%G!+)*C#%!3-)*'!)*!+30,%!6x09G!0*.!'/0'!)'+!+3%,)2),!1-1%*'81! 6p9!!#&-&*&#,).&%!)'+!.%2)*)'%!#-,0')-*!6x9!0'!0##!#0'%&!')1%+!6t9D! p 6M;M9! x(t) = x0 + !t ! me N8+'!0+!B)'/!'/%!0++813')-*!-2!".)/&#%'(0*),&!2-&!0##!-$+%&7%&+!)*!O0#)#%0*!&%#0')7)'4G! '/%+%!,#0++),0#! 0++813')-*+! 0&%! $0+%.! -*! )*'8)')7%! *-')-*+! C&-8*.%.!)*!%7%&4.04!
Load more

Recommended publications
  • 31 Diffraction and Interference.Pdf
    Diffraction and Interference Figu These expar new .5 wave oday Isaac Newton is most famous for his new v accomplishments in mechanics—his laws of Tmotion and universal gravitation. Early in his career, however, he was most famous for his work on light. Newton pictured light as a beam of ultra-tiny material particles. With this model he could explain reflection as a bouncing of the parti- cles from a surface, and he could explain refraction as the result of deflecting forces from the surface Interference colors. acting on the light particles. In the eighteenth and nineteenth cen- turies, this particle model gave way to a wave model of light because waves could explain not only reflection and refraction, but everything else that was known about light at that time. In this chapter we will investigate the wave aspects of light, which are needed to explain two important phenomena—diffraction and interference. As Huygens' Principle origin; 31.1 pie is I constr In the late 1600s a Dutch mathematician-scientist, Christian Huygens, dimen proposed a very interesting idea about waves. Huygens stated that light waves spreading out from a point source may be regarded as die overlapping of tiny secondary wavelets, and that every point on ' any wave front may be regarded as a new point source of secondary waves. We see this in Figure 31.1. In other words, wave fronts are A made up of tinier wave fronts. This idea is called Huygens' principle. Look at the spherical wave front in Figure 31.2. Each point along the wave front AN is the source of a new wavelet that spreads out in a sphere from that point.
    [Show full text]
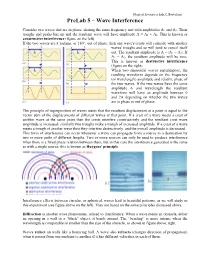
  • Prelab 5 – Wave Interference
    Musical Acoustics Lab, C. Bertulani PreLab 5 – Wave Interference Consider two waves that are in phase, sharing the same frequency and with amplitudes A1 and A2. Their troughs and peaks line up and the resultant wave will have amplitude A = A1 + A2. This is known as constructive interference (figure on the left). If the two waves are π radians, or 180°, out of phase, then one wave's crests will coincide with another waves' troughs and so will tend to cancel itself out. The resultant amplitude is A = |A1 − A2|. If A1 = A2, the resultant amplitude will be zero. This is known as destructive interference (figure on the right). When two sinusoidal waves superimpose, the resulting waveform depends on the frequency (or wavelength) amplitude and relative phase of the two waves. If the two waves have the same amplitude A and wavelength the resultant waveform will have an amplitude between 0 and 2A depending on whether the two waves are in phase or out of phase. The principle of superposition of waves states that the resultant displacement at a point is equal to the vector sum of the displacements of different waves at that point. If a crest of a wave meets a crest of another wave at the same point then the crests interfere constructively and the resultant crest wave amplitude is increased; similarly two troughs make a trough of increased amplitude. If a crest of a wave meets a trough of another wave then they interfere destructively, and the overall amplitude is decreased. This form of interference can occur whenever a wave can propagate from a source to a destination by two or more paths of different lengths.
    [Show full text]
  • Lecture 9, P 1 Lecture 9: Introduction to QM: Review and Examples
    Lecture 9, p 1 Lecture 9: Introduction to QM: Review and Examples S1 S2 Lecture 9, p 2 Photoelectric Effect Binding KE=⋅ eV = hf −Φ energy max stop Φ The work function: 3.5 Φ is the minimum energy needed to strip 3 an electron from the metal. 2.5 2 (v) Φ is defined as positive . 1.5 stop 1 Not all electrons will leave with the maximum V f0 kinetic energy (due to losses). 0.5 0 0 5 10 15 Conclusions: f (x10 14 Hz) • Light arrives in “packets” of energy (photons ). • Ephoton = hf • Increasing the intensity increases # photons, not the photon energy. Each photon ejects (at most) one electron from the metal. Recall: For EM waves, frequency and wavelength are related by f = c/ λ. Therefore: Ephoton = hc/ λ = 1240 eV-nm/ λ Lecture 9, p 3 Photoelectric Effect Example 1. When light of wavelength λ = 400 nm shines on lithium, the stopping voltage of the electrons is Vstop = 0.21 V . What is the work function of lithium? Lecture 9, p 4 Photoelectric Effect: Solution 1. When light of wavelength λ = 400 nm shines on lithium, the stopping voltage of the electrons is Vstop = 0.21 V . What is the work function of lithium? Φ = hf - eV stop Instead of hf, use hc/ λ: 1240/400 = 3.1 eV = 3.1eV - 0.21eV For Vstop = 0.21 V, eV stop = 0.21 eV = 2.89 eV Lecture 9, p 5 Act 1 3 1. If the workfunction of the material increased, (v) 2 how would the graph change? stop a.
    [Show full text]
  • Waves: Interference Instructions: Read Through the Information Below
    Pre-AP Physics Week 2: Day 1 Notes Waves: Interference Instructions: Read through the information below. Then answer the questions below. When two or more waves meet, they interact with each other. The interaction of waves with other waves is called wave interference. Wave interference may occur when two waves that are traveling in opposite directions meet. The two waves pass through each other, and this affects their amplitude. Amplitude is the maximum distance the particles of the medium move from their resting positions when a wave passes through. How amplitude is affected by wave interference depends on the type of interference. Interference can be constructive or destructive. Constructive Interference Destructive Interference Constructive interference occurs when crests of one Destructive interference occurs when the crests of one wave overlap the crests of the other wave. The figure wave overlap the troughs, or lowest points, of another above shows what happens. As the waves pass through wave. The figure above shows what happens. As the each other, the crests combine to produce a wave with waves pass through each other, the crests and troughs greater amplitude. The same can happen with two cancel each other out to produce a wave with zero troughs interacting. amplitude. (NOTE: They don’t always have to fully cancel out. Destructive interference can be partial cancellation.) TRUE or FALSE: Identify the following statements as being either true (T) or false (F). 1. When two pulses meet up with each other while moving through the same medium, they tend to bounce off each other and return back to their origin.
    [Show full text]
  • The Quantum Epoché
    Accepted Manuscript The quantum epoché Paavo Pylkkänen PII: S0079-6107(15)00127-3 DOI: 10.1016/j.pbiomolbio.2015.08.014 Reference: JPBM 1064 To appear in: Progress in Biophysics and Molecular Biology Please cite this article as: Pylkkänen, P., The quantum epoché, Progress in Biophysics and Molecular Biology (2015), doi: 10.1016/j.pbiomolbio.2015.08.014. This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain. ACCEPTED MANUSCRIPT The quantum epoché Paavo Pylkkänen Department of Philosophy, History, Culture and Art Studies & the Academy of Finland Center of Excellence in the Philosophy of the Social Sciences (TINT), P.O. Box 24, FI-00014 University of Helsinki, Finland. and Department of Cognitive Neuroscience and Philosophy, School of Biosciences, University of Skövde, P.O. Box 408, SE-541 28 Skövde, Sweden [email protected] Abstract. The theme of phenomenology and quantum physics is here tackled by examining some basic interpretational issues in quantum physics. One key issue in quantum theory from the very beginning has been whether it is possible to provide a quantum ontology of particles in motion in the same way as in classical physics, or whether we are restricted to stay within a more limited view of quantum systems, in terms of complementary but mutually exclusiveMANUSCRIPT phenomena.
    [Show full text]
  • Time-Domain Grating with a Periodically Driven Qutrit
    PHYSICAL REVIEW APPLIED 11, 014053 (2019) Time-Domain Grating with a Periodically Driven Qutrit Yingying Han,1,2,3,§ Xiao-Qing Luo,2,3,§ Tie-Fu Li,4,2,* Wenxian Zhang,1,† Shuai-Peng Wang,2 J.S. Tsai,5,6 Franco Nori,5,7 and J.Q. You3,2,‡ 1 School of Physics and Technology, Wuhan University, Wuhan, Hubei 430072, China 2 Quantum Physics and Quantum Information Division, Beijing Computational Science Research Center, Beijing 100193, China 3 Interdisciplinary Center of Quantum Information and Zhejiang Province Key Laboratory of Quantum Technology and Device, Department of Physics and State Key Laboratory of Modern Optical Instrumentation, Zhejiang University, Hangzhou 310027, China 4 Institute of Microelectronics, Department of Microelectronics and Nanoelectronics, and Tsinghua National Laboratory of Information Science and Technology, Tsinghua University, Beijing 100084, China 5 Theoretical Quantum Physics Laboratory, RIKEN Cluster for Pioneering Research, Wako-shi, Saitama 351-0198, Japan 6 Department of Physic, Tokyo University of Science, Kagurazaka, Shinjuku-ku, Tokyo 162-8601, Japan 7 Department of Physics, The University of Michigan, Ann Arbor, Michigan 48109-1040, USA (Received 23 October 2018; revised manuscript received 3 December 2018; published 28 January 2019) Physical systems in the time domain may exhibit analogous phenomena in real space, such as time crystals, time-domain Fresnel lenses, and modulational interference in a qubit. Here, we report the experi- mental realization of time-domain grating using a superconducting qutrit in periodically modulated probe and control fields via two schemes: simultaneous modulation and complementary modulation. Both exper- imental and numerical results exhibit modulated Autler-Townes (AT) and modulation-induced diffraction (MID) effects.
    [Show full text]
  • Physical Quantum States and the Meaning of Probability Michel Paty
    Physical quantum states and the meaning of probability Michel Paty To cite this version: Michel Paty. Physical quantum states and the meaning of probability. Galavotti, Maria Carla, Suppes, Patrick and Costantini, Domenico. Stochastic Causality, CSLI Publications (Center for Studies on Language and Information), Stanford (Ca, USA), p. 235-255, 2001. halshs-00187887 HAL Id: halshs-00187887 https://halshs.archives-ouvertes.fr/halshs-00187887 Submitted on 15 Nov 2007 HAL is a multi-disciplinary open access L’archive ouverte pluridisciplinaire HAL, est archive for the deposit and dissemination of sci- destinée au dépôt et à la diffusion de documents entific research documents, whether they are pub- scientifiques de niveau recherche, publiés ou non, lished or not. The documents may come from émanant des établissements d’enseignement et de teaching and research institutions in France or recherche français ou étrangers, des laboratoires abroad, or from public or private research centers. publics ou privés. as Chapter 14, in Galavotti, Maria Carla, Suppes, Patrick and Costantini, Domenico, (eds.), Stochastic Causality, CSLI Publications (Center for Studies on Language and Information), Stanford (Ca, USA), 2001, p. 235-255. Physical quantum states and the meaning of probability* Michel Paty Ëquipe REHSEIS (UMR 7596), CNRS & Université Paris 7-Denis Diderot, 37 rue Jacob, F-75006 Paris, France. E-mail : [email protected] Abstract. We investigate epistemologically the meaning of probability as implied in quantum physics in connection with a proposed direct interpretation of the state function and of the related quantum theoretical quantities in terms of physical systems having physical properties, through an extension of meaning of the notion of physical quantity to complex mathematical expressions not reductible to simple numerical values.
    [Show full text]
  • Consciousness, the Unconscious and Mathematical Modeling of Thinking
    entropy Article On “Decisions and Revisions Which a Minute Will Reverse”: Consciousness, The Unconscious and Mathematical Modeling of Thinking Arkady Plotnitsky Literature, Theory and Cultural Studies Program, Philosophy and Literature Program, Purdue University, West Lafayette, IN 47907, USA; [email protected] Abstract: This article considers a partly philosophical question: What are the ontological and epistemological reasons for using quantum-like models or theories (models and theories based on the mathematical formalism of quantum theory) vs. classical-like ones (based on the mathematics of classical physics), in considering human thinking and decision making? This question is only partly philosophical because it also concerns the scientific understanding of the phenomena considered by the theories that use mathematical models of either type, just as in physics itself, where this question also arises as a physical question. This is because this question is in effect: What are the physical reasons for using, even if not requiring, these types of theories in considering quantum phenomena, which these theories predict fully in accord with the experiment? This is clearly also a physical, rather than only philosophical, question and so is, accordingly, the question of whether one needs classical-like or quantum-like theories or both (just as in physics we use both classical and quantum theories) in considering human thinking in psychology and related fields, such as decision Citation: Plotnitsky, A. On science. It comes as no surprise that many of these reasons are parallel to those that are responsible “Decisions and Revisions Which a for the use of QM and QFT in the case of quantum phenomena.
    [Show full text]
  • On the Interpretation of the Quantum Wave Function
    On the interpretation of the quantum wave function Master's thesis Physics and Astronomy Radboud University Nijmegen Supervisors: Prof. R.H.P. Kleiss and H.C. Donker Second corrector: Assoc. Prof. F. Filthaut Han van der Pluijm August 26, 2016 Contents Introduction 3 1 The wave function and its relation to the real world: Ontic and epistemic interpretations of the wave function 5 1.1 Classical states . .6 1.2 A classical particle in phase space . .7 1.3 Example of an incomplete ontic state . 10 1.4 Quantum states . 11 1.4.1 Epistemic and ontic states in quantum theory . 12 2 Ontological models and the PBR no-go theorem 14 2.1 Ontological models . 15 2.2 The structure of PBR's no-go theorem . 16 2.3 Assumptions . 17 2.3.1 Mathematical equivalents . 18 2.4 The proof . 19 3 Spekkens Toy Theory 23 3.1 The knowledge balance principle . 24 3.2 Spekkens' Toy Bit . 26 3.3 Multiple bits . 31 3.4 Parallels with quantum theory . 33 3.4.1 Convex combinations . 33 3.4.2 Coherent superpositions . 34 3.4.3 Interference . 35 4 Mach-Zehnder interferometer in Spekkens toy theory 36 4.1 Setup of the Mach-Zehnder interferometer . 36 4.2 Quantum behaviour . 38 4.3 States of the MZI in Spekkens' toy theory . 41 4.4 Future prospects . 44 5 Conclusion and discussion 45 Bibliography 47 1 Preface The reason I choose to study physics was twofold. On the one hand I was looking for a challenge and on the other hand I wanted to under- stand the world truly.
    [Show full text]
  • Pilot-Wave Theory, Bohmian Metaphysics, and the Foundations of Quantum Mechanics Lecture 6 Calculating Things with Quantum Trajectories
    Pilot-wave theory, Bohmian metaphysics, and the foundations of quantum mechanics Lecture 6 Calculating things with quantum trajectories Mike Towler TCM Group, Cavendish Laboratory, University of Cambridge www.tcm.phy.cam.ac.uk/∼mdt26 and www.vallico.net/tti/tti.html [email protected] – Typeset by FoilTEX – 1 Acknowledgements The material in this lecture is to a large extent a summary of publications by Peter Holland, R.E. Wyatt, D.A. Deckert, R. Tumulka, D.J. Tannor, D. Bohm, B.J. Hiley, I.P. Christov and J.D. Watson. Other sources used and many other interesting papers are listed on the course web page: www.tcm.phy.cam.ac.uk/∼mdt26/pilot waves.html MDT – Typeset by FoilTEX – 2 On anticlimaxes.. Up to now we have enjoyed ourselves freewheeling through the highs and lows of fundamental quantum and relativistic physics whilst slagging off Bohr, Heisenberg, Pauli, Wheeler, Oppenheimer, Born, Feynman and other physics heroes (last week we even disagreed with Einstein - an attitude that since the dawn of the 20th century has been the ultimate sign of gibbering insanity). All tremendous fun. This week - we shall learn about finite differencing and least squares fitting..! Cough. “Dr. Towler, please. You’re not allowed to use the sprinkler system to keep the audience awake.” – Typeset by FoilTEX – 3 QM computations with trajectories Computing the wavefunction from trajectories: particle and wave pictures in quantum mechanics and their relation P. Holland (2004) “The notion that the concept of a continuous material orbit is incompatible with a full wave theory of microphysical systems was central to the genesis of wave mechanics.
    [Show full text]
  • When the Uncertainty Principle Goes to 11... Or How to Explain Quantum Physics with Heavy Metal
    Ronald E. Hatcher Science on Saturday Lecture Series 12 January 2019 When The Uncertainty Principle goes to 11... or How to Explain Quantum Physics with Heavy Metal Philip Moriarty Professor, University of Nottingham, United Kingdom ABSTRACT: There are deep and fundamental linKs between quantum physics and heavy metal. No, really. There are. Far from being music for Neanderthals, as it’s too often construed, metal can be harmonically and rhythmically complex. That complexity is the source of many connections to the quantum world. You’ll discover how the Heisenberg uncertainty principle comes into play with every chugging guitar riff, what wave interference has to do with Iron Maiden, and why metalheads in mosh pits behave just liKe molecules in a gas. BIOGRAPHY: Philip Moriarty is a professor of physics, a heavy metal fan, a Keen air-drummer, and author of “When The Uncertainty Principle Goes To 11 (or How To Explain Quantum Physics With Heavy Metal” (Ben Bella 2018). His research at the University of Nottingham focuses on prodding, pushing, and poKing single atoms and molecules; in this nanoscopic world, quantum physics is all. Moriarty has taught physics for twenty years and has always been strucK by the number of students in his classes who profess a love of metal music, and by the deep connections between heavy metal and quantum mechanics. A frequent contributor to the Sixty Symbols YouTube channel, which won the Institute of Physics’ Kelvin Award in 2016 for “for innovative and effective promotion of the public understanding of physics”, he has a Keen interest in public engagement, outreach, and bridging the arts-science divide.
    [Show full text]
  • Rethinking a Delayed Choice Quantum Eraser Experiment: a Simple Baseball Model Jeffrey H
    PHYSICS ESSAYS 26, 1 (2013) Rethinking a delayed choice quantum eraser experiment: A simple baseball model Jeffrey H. Boyda) 57 Woods Road, Bethany, Connecticut 06524, USA (Received 10 June 2012; accepted 26 December 2012; published online 26 February 2013) Abstract: In a double slit experiment, you can see an interference fringe pattern or you can know which slit the photon came through, but not both. There are two diametrically opposite theories about why this happens. One is complementarity. The other is the proposal made in this article. An experiment, published in 2000 [Y.-H. Kim et al., Phys. Rev. Lett. 8, 1 (2000)] allegedly supports the idea of complementarity. With different starting assumptions, we arrive at opposite conclusions: complementarity is irrelevant to this experiment. Our assumptions come from the Theory of Elementary Waves. Waves are assumed to travel in the opposite direction: from the detector to the laser. All wave interference is located at the laser. All decisions of importance are located at the laser, not at the detectors. The “decisions” concern which of several elementary rays a photon chooses to follow (this is a probabilistic decision). If a photon is emitted in response to one such impinging ray, all wave interference is then complete. The photon will follow backwards that ray alone, with a probability of one, back to the pair of detectors from which that ray originated. Based on these assumptions, the experiment has nothing to do with complementarity. There is also no delayed choice and no quantum eraser. Conclusion: complementarity is not the only way to understand this experiment.
    [Show full text]