The Physical Origin of Torque and of the Rotational Second Law
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-
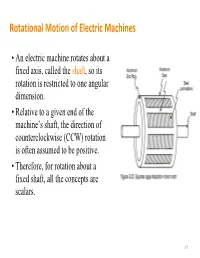
Rotational Motion of Electric Machines
Rotational Motion of Electric Machines • An electric machine rotates about a fixed axis, called the shaft, so its rotation is restricted to one angular dimension. • Relative to a given end of the machine’s shaft, the direction of counterclockwise (CCW) rotation is often assumed to be positive. • Therefore, for rotation about a fixed shaft, all the concepts are scalars. 17 Angular Position, Velocity and Acceleration • Angular position – The angle at which an object is oriented, measured from some arbitrary reference point – Unit: rad or deg – Analogy of the linear concept • Angular acceleration =d/dt of distance along a line. – The rate of change in angular • Angular velocity =d/dt velocity with respect to time – The rate of change in angular – Unit: rad/s2 position with respect to time • and >0 if the rotation is CCW – Unit: rad/s or r/min (revolutions • >0 if the absolute angular per minute or rpm for short) velocity is increasing in the CCW – Analogy of the concept of direction or decreasing in the velocity on a straight line. CW direction 18 Moment of Inertia (or Inertia) • Inertia depends on the mass and shape of the object (unit: kgm2) • A complex shape can be broken up into 2 or more of simple shapes Definition Two useful formulas mL2 m J J() RRRR22 12 3 1212 m 22 JRR()12 2 19 Torque and Change in Speed • Torque is equal to the product of the force and the perpendicular distance between the axis of rotation and the point of application of the force. T=Fr (Nm) T=0 T T=Fr • Newton’s Law of Rotation: Describes the relationship between the total torque applied to an object and its resulting angular acceleration. -

Exploring Robotics Joel Kammet Supplemental Notes on Gear Ratios
CORC 3303 – Exploring Robotics Joel Kammet Supplemental notes on gear ratios, torque and speed Vocabulary SI (Système International d'Unités) – the metric system force torque axis moment arm acceleration gear ratio newton – Si unit of force meter – SI unit of distance newton-meter – SI unit of torque Torque Torque is a measure of the tendency of a force to rotate an object about some axis. A torque is meaningful only in relation to a particular axis, so we speak of the torque about the motor shaft, the torque about the axle, and so on. In order to produce torque, the force must act at some distance from the axis or pivot point. For example, a force applied at the end of a wrench handle to turn a nut around a screw located in the jaw at the other end of the wrench produces a torque about the screw. Similarly, a force applied at the circumference of a gear attached to an axle produces a torque about the axle. The perpendicular distance d from the line of force to the axis is called the moment arm. In the following diagram, the circle represents a gear of radius d. The dot in the center represents the axle (A). A force F is applied at the edge of the gear, tangentially. F d A Diagram 1 In this example, the radius of the gear is the moment arm. The force is acting along a tangent to the gear, so it is perpendicular to the radius. The amount of torque at A about the gear axle is defined as = F×d 1 We use the Greek letter Tau ( ) to represent torque. -

Owner's Manual
OWNER’S MANUAL GET TO KNOW YOUR SYSTEM 1-877-DRY-TIME 3 7 9 8 4 6 3 basementdoctor.com TABLE OF CONTENTS IMPORTANT INFORMATION 1 YOUR SYSTEM 2 WARRANTIES 2 TROUBLESHOOTING 6 ANNUAL MAINTENANCE 8 WHAT TO EXPECT 9 PROFESSIONAL DEHUMIDIFIER 9 ® I-BEAM/FORCE 10 ® POWER BRACES 11 DRY BASEMENT TIPS 12 REFERRAL PROGRAM 15 IMPORTANT INFORMATION Please read the following information: Please allow new concrete to cure (dry) completely before returning your carpet or any other object to the repaired areas. 1 This normally takes 4-6 weeks, depending on conditions and time of year. Curing time may vary. You may experience some minor hairline cracking and dampness 2 with your new concrete. This is normal and does not affect the functionality of your new system. When installing carpet over the new concrete, nailing tack strips 3 is not recommended. This may cause your concrete to crack or shatter. Use Contractor Grade Liquid Nails. It is the responsibility of the Homeowner to keep sump pump discharge lines and downspouts (if applicable) free of roof 4 materials and leaves. If these lines should become clogged with external material, The Basement Doctor® can repair them at an additional charge. If we applied Basement Doctor® Coating to your walls: • This should not be painted over unless the paint contains an anti-microbial for it is the make-up of the coating that prohibits 5 mold growth. • This product may not cover all previous colors on your wall. • It is OK to panel or drywall over the Basement Doctor® Coating. -

Rotation: Moment of Inertia and Torque
Rotation: Moment of Inertia and Torque Every time we push a door open or tighten a bolt using a wrench, we apply a force that results in a rotational motion about a fixed axis. Through experience we learn that where the force is applied and how the force is applied is just as important as how much force is applied when we want to make something rotate. This tutorial discusses the dynamics of an object rotating about a fixed axis and introduces the concepts of torque and moment of inertia. These concepts allows us to get a better understanding of why pushing a door towards its hinges is not very a very effective way to make it open, why using a longer wrench makes it easier to loosen a tight bolt, etc. This module begins by looking at the kinetic energy of rotation and by defining a quantity known as the moment of inertia which is the rotational analog of mass. Then it proceeds to discuss the quantity called torque which is the rotational analog of force and is the physical quantity that is required to changed an object's state of rotational motion. Moment of Inertia Kinetic Energy of Rotation Consider a rigid object rotating about a fixed axis at a certain angular velocity. Since every particle in the object is moving, every particle has kinetic energy. To find the total kinetic energy related to the rotation of the body, the sum of the kinetic energy of every particle due to the rotational motion is taken. The total kinetic energy can be expressed as .. -

Torque Speed Characteristics of a Blower Load
Torque Speed Characteristics of a Blower Load 1 Introduction The speed dynamics of a motor is given by the following equation dω J = T (ω) − T (ω) dt e L The performance of the motor is thus dependent on the torque speed characteristics of the motor and the load. The steady state operating speed (ωe) is determined by the solution of the equation Tm(ωe) = Te(ωe) Most of the loads can be classified into the following 4 general categories. 1.1 Constant torque type load A constant torque load implies that the torque required to keep the load running is the same at all speeds. A good example is a drum-type hoist, where the torque required varies with the load on the hook, but not with the speed of hoisting. Figure 1: Connection diagram 1.2 Torque proportional to speed The characteristics of the charge imply that the torque required increases with the speed. This par- ticularly applies to helical positive displacement pumps where the torque increases linearly with the speed. 1 Figure 2: Connection diagram 1.3 Torque proportional to square of the speed (fan type load) Quadratic torque is the most common load type. Typical applications are centrifugal pumps and fans. The torque is quadratically, and the power is cubically proportional to the speed. Figure 3: Connection diagram 1.4 Torque inversely proportional to speed (const power type load) A constant power load is normal when material is being rolled and the diameter changes during rolling. The power is constant and the torque is inversely proportional to the speed. -

Explanation for Terminology Maxon ECX
Explanation for Terminology maxon ECX Dimensional drawings 14 Speed/torque gradient 29 Number of pole pairs Presentation of the views according to the projection n/M [rpm/mNm] Number of north poles of the permanent magnet. The method E (ISO). The speed/torque gradient is an indicator of the motor’s phase streams and commutation signals pass through All dimensions in [mm]. performance. The smaller the value, the more powerful per revolution p cycles. Servo-controllers require the cor - the motor and consequently the less motor speed varies rect details of the number of pole pairs. Motor Data with load variations. It is based on the quotient of ideal no The values in lines 2–15 are valid when using block com- load speed and ideal stall torque (tolerance ± 20%). 30 Number of phases mutation. With flat motors, the real gradient depends on speed: at All maxon EC motors have three phases. higher speeds, it is steeper, but flatter at lower speeds. 1 Nominal voltage U N [Volt] The real gradient at nominal voltage can be approxi- 31 Weight of motor [g] is the applied voltage between two powered phases in mated by a straight line between no load speed and the 32 Typical noise level [dBA] block commutation. See page 32 for the timing diagram nominal operating point (see page 45). of the voltage in the three phases. All nominal data (lines is that statistical average of the noise level measured according to maxon standard (10 cm distance radially 2–9) refer to this voltage. Lower and higher voltages are 15 Mechanical time constant m [ms] permissible, provided that limits are not exceeded. -

How to Select a Variable Frequency Drive Based on Load Characteristics
How to Select a Variable Frequency Drive Based on Load Characteristics by Vishnuvarthanaraj (Vishnu) Balaraj, Software/Hardware Engineer KB Electronics for more information, email: [email protected] visit: www.kbelectronics.net The most important consideration when choosing a Variable Frequency Drive (VFD) is to know the type of load that is being applied to the motor because it will determine the size and cost of the VFD. The VFD must have sufficient current capability so that the motor can produce the required torque for the load. KB Electronics offers VFDs for AC induction, Permanent Magnet Synchronous Motors (PMSM), and Brushless DC (BLDC) motors that can operate efficiently for various types of loads. Types of Loads Knowing the load profile (speed range, torque, applications. For this kind of use, the VFD must and power) is essential when selecting a suitable be able to provide a high starting torque (1.5 motor and VFD for the application. Generally, times or more the nominal rate) to overcome loads can be grouped into five categories: static friction and inertia of the load. • Constant Torque Loads • Variable Torque Loads • Constant Horsepower Loads • Impact Loads • Starting/Breakaway Type Loads The size of the load, the required speed, and acceleration/deceleration will define the torque and horsepower that is required. The basic equation that relates torque, speed, and horsepower is: Figure 1: Torque – Speed Profile of Constant Torque Loads ���������� = ������ × ����� Figure 1 shows the Torque-Speed and Horsepower-Speed plot for Constant Torque Constant Torque Loads loads. The torque remains constant up to the With constant torque loads, torque is not a base/full speed. -
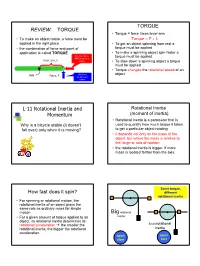
REVIEW: TORQUE TORQUE L-11 Rotational Inertia and Momentum
TORQUE REVIEW: TORQUE • Torque = force times lever arm • To make an object rotate, a force must be Torque = F × L applied in the right place. • To get an object spinning from rest a • the combination of force and point of torque must be applied application is called TORQUE • To make a spinning object spin faster a this force does torque must be applied NOT produce a lever arm, L torque • To slow down a spinning object a torque must be applied • Torque changes the rotational speed of an Axle this force object Force, F produces a torque L-11 Rotational Inertia and Rotational Inertia Momentum (moment of inertia) • Rotational inertia is a parameter that is Why is a bicycle stable (it doesn’t used to quantify how much torque it takes fall over) only when it is moving? to get a particular object rotating • it depends not only on the mass of the object, but where the mass is relative to the hinge or axis of rotation • the rotational inertia is bigger, if more mass is located farther from the axis. Same torque, How fast does it spin? different rotational inertia • For spinning or rotational motion, the rotational inertia of an object plays the same role as ordinary mass for simple motion Big rotational • For a given amount of torque applied to an inertia object, its rotational inertia determines its rotational acceleration Æ the smaller the Small rotational rotational inertia, the bigger the rotational inertia acceleration spins spins slow fast 1 rotational inertia - examples rotational inertia examples Suppose we have a rod of mass 2 kg and length Rods of equal mass and length 1 meter with the axis through the center Its moment of inertia is 2 units axes through center Rotational inertia of 1 unit Imagine now that we take the same rod and stretch it out to 2 meters; its mass is, of course, axes through end the same. -

M34; Torque and Angular Momentum in Circular Motion
TORQUE AND ANGULAR MOMENTUM MISN-0-34 IN CIRCULAR MOTION by Kirby Morgan, Charlotte, Michigan TORQUE AND ANGULAR MOMENTUM 1. Introduction . 1 2. Torque and Angular Momentum IN CIRCULAR MOTION a. De¯nitions . 1 b. Relationship: ~¿ = dL=dt~ . .1 c. Motion Con¯ned to a Plane . 2 d. Circular Motion of a Mass . .3 3. Systems of Particles a. Total Angular Momentum . 4 shaft b. Total Torque . 4 c. Rigid Body Motion About a Fixed Axis . 5 d. Example: Flywheel . 5 e. Kinetic Energy of Rotation . 6 f. Linear vs. Rotational Motion . 6 4. Conservation of Angular Momentum a. Statement of the Law . 7 b. If the External Torque is not Zero . 7 c. Example: Two Flywheels . 7 d. Kinetic Energy of the Two Flywheels . 8 5. Nonplanar Rigid Bodies . 9 Acknowledgments. .9 Glossary . 9 Project PHYSNET·Physics Bldg.·Michigan State University·East Lansing, MI 1 2 ID Sheet: MISN-0-34 THIS IS A DEVELOPMENTAL-STAGE PUBLICATION Title: Torque and Angular Momentum in Circular Motion OF PROJECT PHYSNET Author: Kirby Morgan, HandiComputing, Charlotte, MI The goal of our project is to assist a network of educators and scientists in Version: 4/16/2002 Evaluation: Stage 0 transferring physics from one person to another. We support manuscript processing and distribution, along with communication and information Length: 1 hr; 24 pages systems. We also work with employers to identify basic scienti¯c skills Input Skills: as well as physics topics that are needed in science and technology. A number of our publications are aimed at assisting users in acquiring such 1. -

Keeping Your Torque Wrench Calibrated May Be the Simplest Way to Avoid Broken Fasteners
Foreign Service Keeping your torque wrench calibrated may be the simplest way to avoid broken fasteners. This month, Dan tells us about a company that does the job quickly and efficiently. s a kid, the first things I learned tion vs. a pound of cure. Doubt us? Then con- about wrenchin’ cars—good or sider the cost of labor to pull a job apart again bad—came from the older gear- to remove a busted fastener or repair stripped heads in the neighborhood. And threads caused by inaccurate torque! Dan the first time I ever thought To get the straight scoop on torque wrench about torque wrench accuracy calibration and maintenance, we sought out Marinucci was when one of those older guys broke a Ben Spurlock at Angle Repair and Calibration Ahead bolt while assembling an MG motor. Al- in Beckley, West Virginia (304-253-5720, though the problem generated some cussing, www.anglerepair.com). If this company’s name and a whole lot of theorizing about the cause, rings a bell, it should. If you own an Ameri- the issue went unresolved. Looking back, I can-made torque wrench, the owner’s manual doubt that mechanic thought seriously about for that wrench probably lists Angle Repair as having his torque wrench tested. a factory-authorized repair/calibration source. I don’t think attitudes have changed after all Typically, the first thing a tech wants to these years. That is, torque wrench accuracy know about torque wrench maintenance is and calibration are still probably the farthest how often a wrench needs to be checked. -

Chapter 24 Physical Pendulum
Chapter 24 Physical Pendulum 24.1 Introduction ........................................................................................................... 1 24.1.1 Simple Pendulum: Torque Approach .......................................................... 1 24.2 Physical Pendulum ................................................................................................ 2 24.3 Worked Examples ................................................................................................. 4 Example 24.1 Oscillating Rod .................................................................................. 4 Example 24.3 Torsional Oscillator .......................................................................... 7 Example 24.4 Compound Physical Pendulum ........................................................ 9 Appendix 24A Higher-Order Corrections to the Period for Larger Amplitudes of a Simple Pendulum ..................................................................................................... 12 Chapter 24 Physical Pendulum …. I had along with me….the Descriptions, with some Drawings of the principal Parts of the Pendulum-Clock which I had made, and as also of them of my then intended Timekeeper for the Longitude at Sea.1 John Harrison 24.1 Introduction We have already used Newton’s Second Law or Conservation of Energy to analyze systems like the spring-object system that oscillate. We shall now use torque and the rotational equation of motion to study oscillating systems like pendulums and torsional springs. 24.1.1 Simple -

15. Parallel Axis Theorem and Torque A) Overview B) Parallel Axis Theorem
15. Parallel Axis Theorem and Torque A) Overview In this unit we will continue our study of rotational motion. In particular, we will first prove a very useful theorem that relates moments of inertia about parallel axes. We will then move on to develop the equation that determines the dynamics for rotational motion. In so doing, we will introduce a new quantity, the torque, that plays the role for rotational motion that force does for translational motion. We will find, once again, that the rotational analog of mass will be the moment of inertia. B) Parallel Axis Theorem We have shown earlier that the total kinetic energy of a system of particles in any reference frame is equal to the kinetic energy of the center of mass of the system, defined to be one half times the total mass times the square of the center of mass velocity, plus the kinetic energy of the motion of all of the parts relative to the center of mass. = + K system ,lab K REL KCM For a solid object the only possible motion relative to the center of mass is rotation. Therefore, the kinetic energy relative to the center of mass is just equal to one half times the moment of inertia about a rotation axis through the center of mass times the square of the angular velocity about the center of mass. = 1 ω 2 + 1 2 K system ,lab 2 ICM CM 2 Mv CM We can use this result to calculate the moment of inertia about a chosen axis if the moment of inertia about a parallel axis that passes through the center of mass is known.