Hilbert-Huang Transform Analysis of Surface Wavefield Under Tropical Cyclone Hudhud
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Characteristics of Tropical Cyclonic Storm Phailin As Derived from Satellite and Atmospherics Observations 1R
IJECT VOL . 5, ISSU E SPL - 2, JAN - MAR C H 2014 ISSN : 2230-7109 (Online) | ISSN : 2230-9543 (Print) Characteristics of Tropical Cyclonic Storm Phailin as Derived From Satellite and Atmospherics Observations 1R. Bhattacharya, 2R. Guha, 3J. Pandit, 4A. B. Bhattacharya 1,2Dept. of Environmental Science, University of Kalyani, Kalyani, West Bengal, India 3,4Dept. of Physics, University of Kalyani, Kalyani, West Bengal, India 3Dept. of Physics, JIS School of Polytechnic, Kalyani, West Bengal, India Abstract But on the very next day, Phailin became equivalent to a A summary map concerning the formation of depression and category 4 hurricane on the SSHWS before it underwent an eye cyclonic storms over the North Indian Ocean in the year 2013 wall replacement cycle and formed a new eye wall early on October is first presented pointing out their names, durations and peak 11. This new eye wall further consolidated and allowed the system intensities. The cyclone Phailin originating from North Indian to intensify and become equivalent to a category 5 hurricane on Ocean rapidly developed an eye when it was converted to a very the SSHWS later that day [1-4]. The paper summarizes some severe cyclonic storm on October 10, 2013. Maximum sustained interesting characteristics of the cyclone Phailin and finds its winds are estimated at 195 km/h, gusting to 295 km/h while association with the VLF atmospherics at 27 kHz. minimum central pressure is estimated at 936 hPa with Dvorak intensity of the storm as T6.0. The system subsequently intensified II. Seasons Summary Map and became equivalent to a category 5 hurricane. -

The Impact of Tropical Cyclone Hayan in the Philippines: Contribution of Spatial Planning to Enhance Adaptation in the City of Tacloban
UNIVERSIDADE DE LISBOA FACULDADE DE CIÊNCIAS Faculdade de Ciências Faculdade de Ciências Sociais e Humanas Faculdade de Letras Faculdade de Ciências e Tecnologia Instituto de Ciências Sociais Instituto Superior de Agronomia Instituto Superior Técnico The impact of tropical cyclone Hayan in the Philippines: Contribution of spatial planning to enhance adaptation in the city of Tacloban Doutoramento em Alterações Climáticas e Políticas de Desenvolvimento Sustentável Especialidade em Ciências do Ambiente Carlos Tito Santos Tese orientada por: Professor Doutor Filipe Duarte Santos Professor Doutor João Ferrão Documento especialmente elaborado para a obtenção do grau de Doutor 2018 UNIVERSIDADE DE LISBOA FACULDADE DE CIÊNCIAS Faculdade de Ciências Faculdade de Ciências Sociais e Humanas Faculdade de Letras Faculdade de Ciências e Tecnologia Instituto de Ciências Sociais Instituto Superior de Agronomia Instituto Superior Técnico The impact of tropical cyclone Haiyan in the Philippines: Contribution of spatial planning to enhance adaptation in the city of Tacloban Doutoramento em Alterações Climáticas e Políticas de Desenvolvimento Sustentável Especialidade em Ciências do Ambiente Carlos Tito Santos Júri: Presidente: Doutor Rui Manuel dos Santos Malhó; Professor Catedrático Faculdade de Ciências da Universidade de Lisboa Vogais: Doutor Carlos Daniel Borges Coelho; Professor Auxiliar Departamento de Engenharia Civil da Universidade de Aveiro Doutor Vítor Manuel Marques Campos; Investigador Auxiliar Laboratório Nacional de Engenharia Civil(LNEC) -
Improved Global Tropical Cyclone Forecasts from NOAA: Lessons Learned and Path Forward
Improved global tropical cyclone forecasts from NOAA: Lessons learned and path forward Dr. Vijay Tallapragada Chief, Global Climate and Weather Modeling Branch & HFIP Development Manager Typhoon Seminar, JMA, Tokyo, Japan. NOAA National Weather Service/NCEP/EMC, USA January 6, 2016 Typhoon Seminar JMA, January 6, 2016 1/90 Rapid Progress in Hurricane Forecast Improvements Key to Success: Community Engagement & Accelerated Research to Operations Effective and accelerated path for transitioning advanced research into operations Typhoon Seminar JMA, January 6, 2016 2/90 Significant improvements in Atlantic Track & Intensity Forecasts HWRF in 2012 HWRF in 2012 HWRF in 2015 HWRF HWRF in 2015 in 2014 Improvements of the order of 10-15% each year since 2012 What it takes to improve the models and reduce forecast errors??? • Resolution •• ResolutionPhysics •• DataResolution Assimilation Targeted research and development in all areas of hurricane modeling Typhoon Seminar JMA, January 6, 2016 3/90 Lives Saved Only 36 casualties compared to >10000 deaths due to a similar storm in 1999 Advanced modelling and forecast products given to India Meteorological Department in real-time through the life of Tropical Cyclone Phailin Typhoon Seminar JMA, January 6, 2016 4/90 2014 DOC Gold Medal - HWRF Team A reflection on Collaborative Efforts between NWS and OAR and international collaborations for accomplishing rapid advancements in hurricane forecast improvements NWS: Vijay Tallapragada; Qingfu Liu; William Lapenta; Richard Pasch; James Franklin; Simon Tao-Long -

October 2013 Global Catastrophe Recap 2 2
October 2013 Global Catastrophe Recap Table of Contents Executive0B Summary 3 United2B States 4 Remainder of North America (Canada, Mexico, Caribbean, Bermuda) 4 South4B America 4 Europe 4 6BAfrica 5 Asia 5 Oceania8B (Australia, New Zealand and the South Pacific Islands) 6 8BAAppendix 7 Contact Information 14 Impact Forecasting | October 2013 Global Catastrophe Recap 2 2 Executive0B Summary . Windstorm Christian affects western and northern Europe; insured losses expected to top USD1.35 billion . Cyclone Phailin and Typhoon Fitow highlight busy month of tropical cyclone activity in Asia . Deadly bushfires destroy hundreds of homes in Australia’s New South Wales Windstorm Christian moved across western and northern Europe, bringing hurricane-force wind gusts and torrential rains to several countries. At least 18 people were killed and dozens more were injured. The heaviest damage was sustained in the United Kingdom, France, Belgium, the Netherlands and Scandinavia, where a peak wind gust of 195 kph (120 mph) was recorded in Denmark. More than 1.2 million power outages were recorded and travel was severely disrupted throughout the continent. Reports from European insurers suggest that payouts are likely to breach EUR1.0 billion (USD1.35 billion). Total economic losses will be even higher. Christian becomes the costliest European windstorm since WS Xynthia in 2010. Cyclone Phailin became the strongest system to make landfall in India since 1999, coming ashore in the eastern state of Odisha. At least 46 people were killed. Tremendous rains, an estimated 3.5-meter (11.0-foot) storm surge, and powerful winds led to catastrophic damage to more than 430,000 homes and 668,000 hectares (1.65 million) acres of cropland. -

2013 Major Water-Related Disasters in the World (Pt.1)
2013 Major Water-Related Disasters in the World (Pt.1) India. Nepal (Jun. 2013) Bangladesh (May. 2013) China (May. 2013) China (Aug. 2013) China (Aug. 2013) The Torrential rain by early Landed tropical cyclone Continuous heavy Continuous heavy rain caused The torrential rain by coming monsoon caused MAHASEN brought rain caused floods over-flow the river of border Typhoon Utor, hit China on floods, flash floods and torrential rain and storms. and landslide in area between China and Russia, Aug. 14, caused floods in landslides in northern India and The death toll was 17., and south China. and floods in Northeast China southern China. More than 8 Nepal. The Death toll was about 1.5 million people 55 were killed. and Far East Russia. The death million were affected and 88 6,054 across India, 76 in Nepal were affected. toll was 118 in China. were killed. India (Oct. 2013) The Tropical Cyclone PHAILIN China, Taiwan (Jul. 2013) landed at east coast of India, China (Jan. 2013) Torrential rain caused and killed 47 people. About 1.3 A landslide caused floods and landslides in million people were affected. by the continuous China. And Typhoon heavy rains buried SOULIK lashed Taiwan 16 families, killing India (Oct. 2013) and coastal area of China 46.* th The Flash floods in Odisha on 13 Jul. These killed and Andhra Pradesh, east 233. coast of India, killed 72 people. China, Viet Nam (Sep.2013) The rainstorm by Typhoon Saudi Arabia (Apr.2013) WUTIP caused floods and Continuous heavy rain for 2 Viet Nam (Nov.2013) killed 16 in Viet Nam and 74 weeks caused floods and The torrential rain by Tropical in China. -

Global Catastrophe Review - 2013
An update from GC Analytics© February 2014 GLOBAL CATASTROPHE REVIEW - 2013 2013 provided a respite for the (re)insurance industry following above-average losses in 2011 and 2012, with insured losses from natural catastrophes and man-made disasters estimated at around USD40 billion, according to Guy Carpenter & Company (see Figure 1). This is considerably less than the ten-year average loss of approximately USD60 billion and well below the most significant years of 2005 and 2011 (see Figure 2 (Inflation adjusted)). This can be partly attributed to the unusually quiet 2013 Atlantic tropical season. About 47 percent of insured losses in 2013 were reported in the Americas, 31 percent in Europe and 20 percent in Asia and Australasia (see Figure 3). It is likely that 2013 will be remembered as the “year of the flood,” with significant flood events affecting Central Europe, Australia, the province of Alberta in Canada and Colorado in the United States. Other notable U.S. severe weather events included the outbreaks that produced the Moore, Oklahoma tornado, the El Reno, Oklahoma tornado and the late-season tornado outbreak affecting the Midwestern region. A series of severe weather events, including hail and windstorms, also affected Northern Europe during the second half of the year. Meanwhile, Typhoon Haiyan was established as perhaps the most powerful landfalling tropical cyclone on record, inflicting devastating impacts and loss of life in the Philippines, tragically with well over 7,000 fatalities. 1 2 Europe /Middle East /Africa 2013 will be remembered in Europe in part as the year of the flood, with the worst flood event affecting several Central European countries in June. -

What Is EM-DAT? 7 1.2 Database Definitions, Criteria and Content 7 1.3 Methodology 9 1.4 Disaster Classification 10
Centre for Research on the Epidemiology of Disasters (CRED) Annual Disaster Statistical Review 2013 The numbers and trends Debarati Guha-Sapir, Philippe Hoyois and Regina Below Annual Disaster Statistical Review 2013 The numbers and trends Debarati Guha-Sapir Philippe Hoyois and Regina Below Centre for Research on the Epidemiology of Disasters (CRED) Institute of Health and Society (IRSS) Université catholique de Louvain – Brussels, Belgium Acknowledgements The data upon which this report is based on, is maintained through the long-term support of the US Agency for International Development’s Office of Foreign Disaster Assistance (USAID/OFDA). We are grateful to Pascaline Wallemacq for designing the graphs and maps and to Simone M’Bala for proofreading We encourage the free use of the contents of this report with appropriate and full citation: “Guha-Sapir D, Hoyois Ph. , Below. R. Annual Disaster Statistical Review 2013: The Numbers and Trends. Brussels: CRED; 2014.” This document is available on http://www.cred.be/sites/default/files/ADSR_2013.pdf Printed by: Ciaco Imprimerie, Louvain-la-Neuve (Belgium) This publication is printed in an environmentally - friendly manner. September 2014 ii Annual Disaster Statistical Review 2013 – The numbers and trends About CRED The Centre for Research on the Epidemiology of Disasters (CRED) has been active for more than 40 years in the fields of: international disaster and conflict health studies, research and training activities linking relief, rehabilitation, and development. It was established in Brussels in 1973 at the School of Public Health of the Catholic University of Louvain (UCL) as a non-profit institution with international status under Belgian law. -

A Review on Management of Cyclone Phailin 2013 in Odisha
Original Research A review on Management of cyclone Phailin 2013 in Odisha Gouri Kumari Padhy1, Abhisek Mishra2,*, Sangeeta Das3, Rabi Narayan Padhy4, Jeetendra Kumar Padhy5 1Associate Professor, 2Senior Resident, Dept. of CFM, AIIMS, Raipur, 3Assistant Professor, Dept of psm, MKCG Medical College, Odisha 4AYUSH Medical Officer, Kanheipur, Khallikote, Dist: Ganjam, Odisha 5Ex Faculty, Vani Vihar University, BBSR, Odisha *Corresponding Author: E-mail: [email protected] ABSTRACT Background: On 12th Oct 2013 Cyclonic storm “Phailin” had caused heavy rainfall and massive flooding in Odisha (a state in India's eastern belt). It had affected more than 13.2 million people. The estimated cost of total damage was Rs. 14373.47 crore including devastation to houses, crops and public properties. The destruction to power supply system, communication system and transport system was of massive degree. Objectives: To assess management of the cyclone “Phailin”. Methodology: A cross sectional study was carried out for seven months in and around Berhampur city (the most affected area). Data were collected from primary and secondary sources. Results: Evacuation and relocation of approximately 1.2 million people could had been possible due to early warning alerts, disseminated four days prior to landfall of Phailin, resulting in the largest evacuation operation of India in last 23 years. A total 21 lives were lost as a result of the cyclone and an additional 23 lives due to severe flash flooding in the aftermath of the cyclone. Conclusion: A comparable cyclone, (Cyclone 05B) hit Odisha with wind speed of about 260 km/h, resulted in loss of more than 10,000 lives in 1999. -

Reviewer 1 >>> We Would Like to Thank the Anonymous Reviewer For
Reviewer 1 >>> We would like to thank the anonymous reviewer for the insightful and constructive comments, which helped us to improve our manuscript. We appreciate the valuable comments and try to address the issues raised as best as possible. According to the suggestions, we changed the data set structure. For each yearly folder, we created a set of subfolders with respect to the different ocean basin. However, the archive will be updated when the discussion will be closed so the paper remains consistent with the dataset structure. Each major comment has been carefully considered point by point and responded below. Major Comments/Suggestions I have one major comment to the data set. When open the data link, I have found the data set in a specific folder with the name of individual years (2001, 2002,...2018). Some of the data files are having the name like‘NOT_NAMED_2001_2001031S13072.nc’ in each folder of individual years. This will create some confusion for the users. It would be useful to provide sub folders with respect to each oceanic basin for each year. I strongly suggest to the authors, please include the subfolders with respect to the different ocean basin and keep the data files with respect to basins. I hope this may not take much time for the authors. >>> Thank you for the suggestion. We changed the data structure and every yearly folder is divided on subfolders related to the ocean basins. Hopefully, it makes the access to the dataset clearer for the users now. However, since a single TC can pass through many ocean basins, we assign every TC to the origin ocean basin, where the corresponding TC has started. -

Simulation and Validation of INSAT-3D Sounder Data at NCMRWF S
Simulation and Validation of INSAT-3D sounder data at NCMRWF S. Indira Rani and V. S. Prasad National Centre for Medium Range Weather Forecasting (NCMRWF) Earth System Science Organization (ESSO) Ministry of Earth Sciences (MoES) Government of India A-50, Sector-62, Noida, Uttar Pradesh-201309, India. Email: [email protected], [email protected] Abstract India's advanced weather satellite, INSAT-3D, the first geostationary sounder system over Indian Ocean, was launched (located at 83°E) on 26 July 2013, for the improved understanding of mesoscale systems. INSAT-3D carries a 6 channel imager and 19 channel sounder payload. Along with other polar satellite soundings, INSAT-3D provides fine resolution vertical profiles over India and surrounding region. National Centre for Medium Range Weather Forecasting (NCMRWF) routinely receives near-real time soundings from polar orbiting satellites, and recently started receiving INSAT- 3D sounder and imager data. Simulation of INSAT-3D sounder Brightness Temperature (BT) using Radiative Transfer models and Numerical Weather prediction models has been done at NCMRWF during the North Indian Ocean Cyclone (NIOC) period of 2013. BTs during four different cyclones, viz., Phailin, Helen, Lehar and Madi are simulated and validated against the observed BTs. The RT model used to simulate the BT is Radiative Transfer for TOVS (RTTOV) version-9 and the NWP model used is Direct Broadcast CIMSS Regional Assimilation System (dbCRAS). Clear sky condition is assumed during RTTOV simulation, though the cloudy pixels are not removed, since the cloud information is not available in the then dataset. RT model simulated sounder BT of three channels (12.66 µ, 12.02µ and 11.03 µ) and DbCRAS simulated 11 µ BTs are compared with the corresponding INSAT-3D sounder BTs. -

BACKGROUND on the 8Th October 2013, the Indian Meteorological
BACKGROUND picture painted by Cyclone Phailin should be one of the OUTCOME On the 8 th October 2013, the Indian Meteorological nation’s successes in disaster mitigation in the face of The workshop would be helpful to compile all Department reported about the formation of a severe climatic conditions. information in the form of a document and disseminate depression. As the cyclone was expected to make a the same to all concerned for better resilience. landfall on the 12 th October, the states of Odisha and The unfolding tragedy in the states of Odisha and Andhra Andhra Pradesh witnessed the greatest evacuation in Pradesh has raised the inevitable question: how can we CHIEF GUEST Indian history with over 13 lakh people evacuated. better our preparedness. In order to share the learning Dr. K. Saleem Ali, Hon’ble Member, NDMA, New Delhi The Army, Air Force, NDRF, ODRAF, CRPF, Public Works experience from all the government and non- Department and local administration were prepared to government organisations involved in the planning, PROGRAMME work together for evacuation and quick rescue preparedness, evacuation, rescue, relief and operations. Activists from political and social rehabilitation, NIDM is organising one day workshop on Time Session Speakers organizations were also involved in the rescue and “Lessons Learnt from Cyclone Phailin”. (hrs) management of relief centres. The national highways 0900 – Registration NIDM staff 1000 and other important roads were closed to regular traffic. OBJECTIVES 1000 – Inaugural Session Welcome Address – ED Helicopters and various other alternate modes of • To collate information and share 1040 NIDM transport were used to rescue people and take them to knowledge/experiences about the impacts of the Address by Guest of safe shelters. -
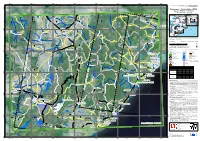
200 Dpi) N " 0 ' 0 °
! 600000 650000 700000 750000 800000 850000 900000 ! 950000 82°0'0"E 82°30'0"E 83°0'0"E 83°30'0"E 84°0'0"E 84°30'0"E 85°0'0"E ! GLIDE number: TC-2013-000133-IND Activation ID: EMSR-057 0 0 0 0 Product N.: 02BRAHMAPUR, v1 0 0 0 0 0 0 3 3 2 2 Brahmapur - Odisha State - INDIA ! Cyclone Phailin - 12/10/2013 X Delineation Map - Overview (! (! Production date: 03/11/2013 Dhenkanal Brahmaputra (! Uttar Dhaka Pradesh Bihar Rajshahi Madhya (! biCbhhinaag Cuttack PakistRanajshahi bibhag Agartala Pradesh Nepal (! ^ DBhhauktaan N Jharkhand New Bangladesh " ^ 0 ' Ranchi Delhi Khulna Balak M 0 Chittagong 3 S ! bibhag ° ( a West s bibhag 0 N o Sa Khulna 2 a n n h a rm da e ! Myanmar a k ( n India g (! N a h Bengal " d n ! Barisal 0 i ( (! ' R a 0 Balangir iv r 3 e G Kolkata ° Arabian 0 X Titlagarn Bay of 2 Chhattisgarh Sea Bengal Hinakud Dam Sri Andaman Laccadive Sea (! Raipur Sea Lanka B ahm r a n i Ma l ha (! Te na 0 0 di 0 0 Bhubaneshwar 0 0 Odisha 0 Phulabani 0 Bay of 5 5 Bengal 2 2 d Brahmapur (! 2 Kesinga 2 In ra vati ! X Raipur Titlagarh Junction Godavari Andhra Madhya X! Pradesh Pradesh Kesinga Puri Cartographic Information 1:55! 0000 Full color ISO A1, medium resolution (200 dpi) N " 0 ' 0 ° 0 0 10 20 40 2 km N " 0 ' 0 ° 0 Grid: WGS 1984 UTM Zone 44N map coordinate system 2 Kalahandi !Bhanjanagar Tick marks: WGS 84 geographical coordinate system ± ! 0 0 0 0 Legend 0 Bhawanipatna 0 0 0 0 0 Crisis Information Hydrology Transportation r 2 2 2 2 Flooded Area (02/11/2013 12:09 - 12:33) Dam Aerodrome Salia X W ! Reservoir General Information River