Improved Large-Scale Hydrological Modelling Through the Assimilation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

AWAP): CSIRO Marine and Atmospheric Research Component: Final Report for Phase 3
The Centre for Australian Weather and Climate Research A partnership between CSIRO and the Bureau of Meteorology Australian Water Availability Project (AWAP): CSIRO Marine and Atmospheric Research Component: Final Report for Phase 3 M.R. Raupach, P.R. Briggs, V. Haverd, E.A. King, M. Paget and C.M. Trudinger CAWCR Technical Report No. 013 July 2009 Australian Water Availability Project (AWAP): CSIRO Marine and Atmospheric Research Component: Final Report for Phase 3 M.R. Raupach, P.R. Briggs, V. Haverd, E.A. King, M. Paget and C.M. Trudinger CAWCR Technical Report No. 013 July 2009 Centre for Australian Weather and Climate Research, a Partnership between the Bureau of Meteorology and CSIRO, Melbourne, Australia ISSN: 1836-019X National Library of Australia Cataloguing-in-Publication entry Title: Australian Water Availability Project (AWAP) : CSIRO Marine and Atmospheric Research Component : Final Report for Phase 3 / M.R. Raupach ... [et al.] ISBN: 9781921605314 (pdf) Series: CAWCR technical report ; no. 13. Notes: Bibliography. Subjects: Hydrology--Australia. Hydrologic models--Australia. Water-supply—Australia—Mathematical models. Other Authors/Contributors: Raupach, M.R. (Michael Robin) Australia. Bureau of Meteorology. Centre for Australian Weather and Climate Research. Australia. CSIRO and Bureau of Meteorology. Dewey Number: 551.480994 Enquiries should be addressed to: Dr Michael Raupach CSIRO Marine and Atmospheric Research Global Carbon Project GPO Box 3023, Canberra ACT 2601 Australia [email protected] Copyright and Disclaimer © 2009 CSIRO and the Bureau of Meteorology. To the extent permitted by law, all rights are reserved and no part of this publication covered by copyright may be reproduced or copied in any form or by any means except with the written permission of CSIRO and the Bureau of Meteorology. -

Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources Amendment Order 2016 Under The
New South Wales Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources Amendment Order 2016 under the Water Management Act 2000 I, Niall Blair, the Minister for Lands and Water, in pursuance of sections 45 (1) (a) and 45A of the Water Management Act 2000, being satisfied it is in the public interest to do so, make the following Order to amend the Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources 2012. Dated this 29th day of June 2016. NIALL BLAIR, MLC Minister for Lands and Water Explanatory note This Order is made under sections 45 (1) (a) and 45A of the Water Management Act 2000. The object of this Order is to amend the Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources 2012. The concurrence of the Minister for the Environment was obtained prior to the making of this Order as required under section 45 of the Water Management Act 2000. 1 Published LW 1 July 2016 (2016 No 371) Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources Amendment Order 2016 Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources Amendment Order 2016 under the Water Management Act 2000 1 Name of Order This Order is the Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources Amendment Order 2016. 2 Commencement This Order commences on the day on which it is published on the NSW legislation website. 2 Published LW 1 July 2016 (2016 No 371) Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources Amendment Order 2016 Schedule 1 Amendment of Water Sharing Plan for the Murrumbidgee Unregulated and Alluvial Water Sources 2012 [1] Clause 4 Application of this Plan Omit clause 4 (1) (a) (xxxviii) and (xxxix). -

EIS 968 Environmental Impact Statement for Proposed Sand, Soil and Gravel Extraction at Bredbo in the Shire of Cooma-Monaro
EIS 968 Environmental impact statement for proposed sand, soil and gravel extraction at Bredbo in the Shire of Cooma-Monaro NSW DEPT PEIApy 1NDUSpp1 IIIIIIiu!IIIIIihIIIIih////I/II//II/ll/II///IIjI ABOi 9636 ENVIRONMENTkL IKPACT STAThMENT for proposed Sand, Soil and Gravel Extraction at Bredbo in the Shire of Cooma-Monaro prepared for Lee Aggregates Pty.Ltd. by D.P.JAMES APRIL 1991 Lee Aggregates Pty.Ltd.. D.P.JAMES & COMPANY P.O.Box 397, P.O.Box 170, WANNIASSA, 2903. KOGARAH, 2217. (062)92.3961. (02)588.2614. I I I I I I I I I I I I I I I I I I C ENVIRONMENTAL IMPACT STATEMENT Prepared by D.P.Jaines on behalf of Lee Aggregates Pty.Ltd., P.O.Box 397, Wanniassa, 2903, A.C.T. This is the second edition of this environmental impact statement and is dated April 1991. The first edition is dated June 1988. Minor spelling and typographical errors have been corrected in the second edition, which has been laser printed. '000d-~; 9 April 1991. D.P.James, ARMIT, AMIQ, AIMM. 5/2 Hardie Street, P0 Box 653, 1 NEUTRAL BAY 2089 1- (02)904 1515. / j I 1 INTRODUCTION 1.1 General 1.2 Summary of Proposed Development I 1.3 Development Objectives I 2. EXISTING ENVIRONMENT 2.1 Zoning 22 Landforin 2.3 Land Use I 2.4 Climate & Flooding 2.5 Air Quality 2.6 Water Quality I 2.6.1 Murrunthidgee River 2.7 Noise 2.8 Flora I 2.9 Fauna 2.10 Traffic 2.11 Economic Aspects 2.12 Social & Cultural Aspects Ii 2.13 Archaeology 2.14 Soil & Water Conservation Matters I 2.15 Extractive Industry I ENVIRONMENTAL IMPACTS & PROTECTION MEASURE 3.1 Land Use 3.2 Climate & Flooding 3.3 -

Laura and Jack Book 1.Pdf
Laura & Jack – In time they go back What connects these two girls born close to 100 years apart? Emily’s family move from Sydney to Adelong in the South-West slopes of New South Wales in June 2015. Her mother grew up there and her father has taken up a teaching position nearby. Emily, aged eight, and her younger brother, Gary, have to change schools mid year. When she puts away her clothes she finds an old diary wedged at the back of a set of drawers. It belongs to Laura, born in 1920. Emily takes a journey through Laura’s life seeing how things have changed, yet stayed the same in some ways. Laura’s diary covers her life as a child in the early 1900s and that of her best friends, Cathy, Jack, Billy and Jean. Jack is based on a real person; an Aussie larrikin and country lad struggling to earn money during the 1920s and Depression to help his family. His positive outlook sees him through. He continues to return home and writes to Laura after he leaves school, aged thirteen. Emily makes new friends at her new school; Amy, part Aboriginal, Shannon and Chase. She goes exploring around the Riverina and high country with her family learning about history and the environment. She also learns she has a connection to Laura. * In book two they grow older and further connections entwine Jack and Laura with Chase and Emily. 2 Laura & Jack – In time they go back Chapter Book One LAURA & JACK - In time they go back For Primary School age and young teenager 8 to 13 A story of two young girls in different times, their loves and losses and lives entwined Author Sharon Elliott Cover: Adobe Spark 3 Laura & Jack – In time they go back Disclaimer This is a work of fiction. -

Pp4969 Snowy Monaro Regional Council
WILLIAMSDALE ! THE Ref: PP4969 ANGLE ! BURRA A U S T R A L II A N Local Government Area Boundary CLEAR LONG C A P I T A L RANGE JINGERA PLAIN C A P I T A L MICHELAGO SNOWY MONARO TANTANGARA T E R R II T O R Y REGIONAL COUNCIL TINDERRY ANEMBO Legend YAOUK KOSCIUSZKO NATIONAL BUMBALONG PARK ! Local Government Area ! COLINTON Hydro Area JERANGLE Suburb BOLARO PROVIDENCE PORTAL ! ! Road BREDBO SHANNONS Railway Legend FLAT Watercourse ANGLERS ¦ REACH BILLILINGRA PEAK OLD ADAMINABY VIEW Scale 1:700,000 Datum: GDA 94 ADAMINABY BADJA CHAKOLA DRY BRAEMAR PLAIN BAY MURRUMBUCCA EUCUMBENE ! ROSE Local Government Area (LGA) boundaries and names as proclaimed in ! VALLEY proclamation made under the Local Government Act 1993 notified in the SNOWY FRYING BUNYAN PLAIN BUCKENDERRA PAN NSW Government Gazette on 12/05/2016. NIMMO RHINE FALLS WAMBROOK BINJURA NUMERALLA This plan constitutes a Public Survey as described in section 7, part 2 of COUNTEGANY POLO F! LAT GLEN the Surveying and Spatial Information Act 2002. MIDDLINGBANK DAIRYMANS ! FERGUS PLAINS MIDDLE ROCKY FLAT Source: ! COOMA PLAIN COOLRINGDON PINE ! CARLAMINDA Digital data used in this plan has been sourced from Land and Property VALLEY TUROSS COOTRALANTRA WADBILLIGA Information (LPI). ! DANGELONG ! KALKITE ! ! HILL The pre-existing Local Government Area boundaries and names are TOP SNOWY MONARO REGIONAL COUNCIL sourced from the Digital Cadastral Database (DCDB) and agree with BERRIDALE THE those as at the date of extraction. The cadastral fabric used AVONSIDE ARABLE BROTHERS ROCK KYBEYAN to produce this plan was extracted from the DCDB. The DCDB is linked EAST FLAT JINDABYNE to the NSW State Control Survey. -

'Geo-Log' 2012
‘Geo-Log’ 2012 Journal of the Amateur Geological Society of the Hunter Valley ‘Geo-Log’ 2012 Journal of the Amateur Geological Society of the Hunter Valley Inc. Contents: President’s Introduction 2 Australian Alps Safari 3 New Hartley Excursion 20 Redhead Bluff: Stratigraphy and Paleoenvironment 29 Varved Shale in the Seaham and Raymond Terrace Area 33 Coolah Tops NP Weekend 37 Some Regional Geology of the Eyre Peninsula, South Australia: Geological Safari 2012 43 Geo-Log 2012 - Page 1 President’s Introduction. Hello members and friends, Yet again we have enjoyed a very successful year. Although the Society has been running for over 30 years, our membership has remained stable and has even increased slightly in recent years, reflecting a continuing enthusiasm for and appreciation of the earth sciences and related activities. A background in geology is not a prerequisite to membership and every member is strongly encouraged to take part regardless of their level of knowledge. Although the initial aim of the Society was the exploration and understanding of Hunter Valley geolo- gy, for several years now we have continued to widen our coverage well beyond the confines of the Valley. Even so, while the organizing committee tries to include new activities into the program each year, this is becoming more difficult. But new members bring new ideas and new experiences which everyone can benefit from. Occasionally old sites are revisited, either for the benefit of new members or where the availability of new information has allowed a greater understanding of earth history. Our first extended excursion was organized (with some trepidation) into the Flinders Ranges in 1995, but this was so successful that similar trips have since taken place annually. -

Sendle Zones
Suburb Suburb Postcode State Zone Cowan 2081 NSW Cowan 2081 NSW Remote Berowra Creek 2082 NSW Berowra Creek 2082 NSW Remote Bar Point 2083 NSW Bar Point 2083 NSW Remote Cheero Point 2083 NSW Cheero Point 2083 NSW Remote Cogra Bay 2083 NSW Cogra Bay 2083 NSW Remote Milsons Passage 2083 NSW Milsons Passage 2083 NSW Remote Cottage Point 2084 NSW Cottage Point 2084 NSW Remote Mccarrs Creek 2105 NSW Mccarrs Creek 2105 NSW Remote Elvina Bay 2105 NSW Elvina Bay 2105 NSW Remote Lovett Bay 2105 NSW Lovett Bay 2105 NSW Remote Morning Bay 2105 NSW Morning Bay 2105 NSW Remote Scotland Island 2105 NSW Scotland Island 2105 NSW Remote Coasters Retreat 2108 NSW Coasters Retreat 2108 NSW Remote Currawong Beach 2108 NSW Currawong Beach 2108 NSW Remote Canoelands 2157 NSW Canoelands 2157 NSW Remote Forest Glen 2157 NSW Forest Glen 2157 NSW Remote Fiddletown 2159 NSW Fiddletown 2159 NSW Remote Bundeena 2230 NSW Bundeena 2230 NSW Remote Maianbar 2230 NSW Maianbar 2230 NSW Remote Audley 2232 NSW Audley 2232 NSW Remote Greengrove 2250 NSW Greengrove 2250 NSW Remote Mooney Mooney Creek 2250 NSWMooney Mooney Creek 2250 NSW Remote Ten Mile Hollow 2250 NSW Ten Mile Hollow 2250 NSW Remote Frazer Park 2259 NSW Frazer Park 2259 NSW Remote Martinsville 2265 NSW Martinsville 2265 NSW Remote Dangar 2309 NSW Dangar 2309 NSW Remote Allynbrook 2311 NSW Allynbrook 2311 NSW Remote Bingleburra 2311 NSW Bingleburra 2311 NSW Remote Carrabolla 2311 NSW Carrabolla 2311 NSW Remote East Gresford 2311 NSW East Gresford 2311 NSW Remote Eccleston 2311 NSW Eccleston 2311 NSW Remote -

Functioning and Changes in the Streamflow Generation of Catchments
Ecohydrology in space and time: functioning and changes in the streamflow generation of catchments Ralph Trancoso Bachelor Forest Engineering Masters Tropical Forests Sciences Masters Applied Geosciences A thesis submitted for the degree of Doctor of Philosophy at The University of Queensland in 2016 School of Earth and Environmental Sciences Trancoso, R. (2016) PhD Thesis, The University of Queensland Abstract Surface freshwater yield is a service provided by catchments, which cycle water intake by partitioning precipitation into evapotranspiration and streamflow. Streamflow generation is experiencing changes globally due to climate- and human-induced changes currently taking place in catchments. However, the direct attribution of streamflow changes to specific catchment modification processes is challenging because catchment functioning results from multiple interactions among distinct drivers (i.e., climate, soils, topography and vegetation). These drivers have coevolved until ecohydrological equilibrium is achieved between the water and energy fluxes. Therefore, the coevolution of catchment drivers and their spatial heterogeneity makes their functioning and response to changes unique and poses a challenge to expanding our ecohydrological knowledge. Addressing these problems is crucial to enabling sustainable water resource management and water supply for society and ecosystems. This thesis explores an extensive dataset of catchments situated along a climatic gradient in eastern Australia to understand the spatial and temporal variation -

Annual Operations Plan Murrumbidgee Valley 2019-20 Acronym Definition
Annual Operations Plan Murrumbidgee Valley 2019-20 Acronym Definition Available Water Contents AWD Determination Introduction 2 BLR Basic Landholder Rights The Murrumbidgee River System 2 Regulated and unregulated system flow trends 3 BoM Bureau of Meteorology Rainfall trends 3 CWAP Critical Water Advisory Panel Inflows to dam 4 Critical Water Technical Water users in the valley 4 CWTAG Advisory Group Water availability 7 Department of Primary Current drought conditions 9 DPI CDI Industries - Combined Blowering Dam storage 10 Drought Indicator Burrinjuck Dam storage 10 Department of Planning, Inter valley transfer 11 Industry and Environment - DPIE EES Operational surplus 12 Environment, Energy & Science Transmission losses 12 Resource assessment 15 DPI Department of Primary End of System flow targets 17 Fisheries Industries - Fisheries Department of Planning, Water resource forecast 18 DPIE Industry and Environment - Water Murrumbidgee catchment - past 24 month rainfall 18 Water Blowering Dam - past 24 month inflows/statistical inflows 19 FSL Full Supply Level Burrinjuck Dam - past 24 month inflows/statistical inflows 19 Weather forecast - 3 month BoM forecast 20 HS High Security Murrumbidgee storage forecast 20 IRG Incident Response Guide Annual operations 22 Infrastructure State ISEPP Environmental Planning Operational rules 22 Policy Deliverability 24 Overall scenario assumptions 24 LGA Local Government Areas River Operations Stakeholder ROSCCo Critical dates 25 Consultation Committee S&D Stock & Domestic Potential projects 26 Valley Technical Advisory vTAG Group Introduction The annual operations plan provides an outlook for the coming year in the Murrumbidgee Valley and considers the current volume of water in storages and weather forecasts. This plan may be updated as a result of significant changes to the water supply situation. -

Snowy Valleys Council Local Strategic Planning Statement June 2020 CONTENTS
ENVISAGE 2040: Our Path to a Sustainable Future LOCAL STRATEGIC PLANNING STATEMENT Spatial Land Use Concepts 1 Snowy Valleys Council Local Strategic Planning Statement June 2020 CONTENTS INTRODUCTION ABOUT THIS STATEMENT 4 POLICY FRAMEWORK 4 CONSULTATION 6 CONTEXT OUR REGION 7 OUR ECONOMY 8 OUR COMMUNITIES 9 OUR CHALLENGES 22 OUR ENVIRONMENT 23 SNOWY VALLEYS: OUR VISION 24 ACHIEVING OUR VISION 25 TOWNS AND VILLAGES 26 GROWTH THROUGH INNOVATION 31 OUR NATURAL ENVIRONMENT 35 OUR INFASTRUCTURE 41 REFERENCES 56 MAPPING 57 2 Snowy Valleys Council Local Strategic Planning Statement June 2020 ACKNOWLEDGEMENT OF COUNTRY We acknowledge the traditional custodians of this land and pay respects to Elders past and present. We recognise Aboriginal people as the original custodians of the lands that comprise the Snowy Valleys Council area and pay our respects to the leaders of the traditional custodians of this land. Together we acknowledge the contributions of Aboriginal Australians to this country we all live in and share together. Snowy Valleys Council is committed to enhancing the knowledge and understanding of our communities about the history, heritage and cultures of Aboriginal Australians. Snowy Valleys Council Local Strategic Planning Statement June 2020 3 INTRODUCTION About this Statement A 20-year planning vision espoused in the Local Strategic Planning Statement emphasises economic, social and spatial land use intentions for the Snowy Valleys Council area. The Local Strategic Planning Statement sets clear local priorities for employment, housing, services and infrastructure that the Snowy Valleys communities will require over the next 20 years. The Statement sets short, medium and long-term actions linked to local priorities, enabling delivery of the community’s future vision. -

Hydromys Chrysogaster) in the GREATER ACT REGION
DISTRIBUTION AND STATUS OF THE AUSTRALIAN WATER-RAT/RAKALI (Hydromys chrysogaster) IN THE GREATER ACT REGION A REPORT BY THE AUSTRALIAN PLATYPUS CONSERVANCY TO THE WETTENHALL ENVIRONMENT TRUST G. A. Williams SEPTEMBER 2019 DISTRIBUTION AND STATUS OF THE AUSTRALIAN WATER-RAT/RAKALI (Hydromys chrysogaster) IN THE GREATER ACT REGION SUMMARY The Australian water-rat or rakali* (Hydromys chrysogaster) is an exceptionally difficult species to survey using conventional live-trapping techniques. Consequently, relatively little is known about the current distribution and status of this very attractive native mammal in most parts of its range. This, in turn, has contributed to limited public awareness of rakali’s occurrence and its important ecological role as a top aquatic predator. This community-based survey, supported by the Wettenhall Environment Trust, has taken an important step in addressing the shortfall in knowledge about this species. New rakali reports contributed by this project represent a 526% increase on the pre-existing total of records for the Greater ACT region for the 2010-2019 period. The newly aggregated records and other relevant data were collated to allow a broad assessment of how water-rats are faring across the region – i.e. the ACT and neighbouring sections of NSW. This work also established a baseline for future sightings-based monitoring, and helped identify useful directions for further research. The project also demonstrated that there is considerable potential for improving public support for water-rats as very desirable residents of waterways. Community interest in local rakali populations can potentially now be harnessed by relevant management agencies to highlight and help address environmental problems along waterways, particularly in areas where the more iconic platypus does not occur or is less common. -
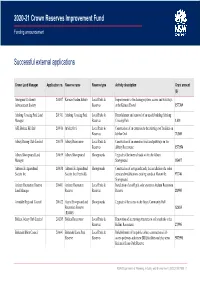
Full List of the 2020-21 Successful Applicants
2020-21 Crown Reserves Improvement Fund Funding announcement Successful external applications Crown Land Manager Application no. Reserve name Reserve type Activity description Grant amount ($) Aboriginal Children's 200817 Kirinari Garden Suburb Local Parks & Improvements to the drainage system, access and walkways Advancement Society Reserves at the Kirinari Hostel 157,769 Adelong Crossing Park Land 201511 Adelong Crossing Park Local Parks & Demolishment and removal of an unsafe building Adelong Manager Reserves Crossing Park 1,331 AFL Broken Hill Ltd 200910 Jubilee Oval Local Parks & Construction of an extension to the existing roof facilities on Reserves Jubilee Oval 71,369 Albury Racing Club Limited 200175 Albury Racecourse Local Parks & Construction of an amenities block and pathways on the Reserves Albury Racecourse 157,956 Albury Showground Land 200059 Albury Showground Showgrounds Upgrade of the internal roads within the Albury Manager Showground 35,417 Alstonville Agricultural 200058 Alstonville Agricultural Showgrounds Construction of new grandstands, the installation of a rodeo Society Inc Society Inc (Freehold) arena and modifications existing stands at Alstonville 97,746 Showground Araluen Recreation Reserve 200411 Araluen Recreation Local Parks & Installation of an off grid solar system at Araluen Recreation Land Manager Reserve Reserves Reserve 28,995 Armidale Regional Council 201622 Guyra Showground and Showgrounds Upgrade of the access to the Guyra Community Hall Recreation Reserve 62,833 (R84003) Ballina Jockey Club Limited