DOCSLIB.ORG

Addis Ababa University School of Graduate Studies Department of Statistics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Addis Ababa University School of Graduate Studies Department of Statistics ADDIS ABABA UNIVERSITY SCHOOL OF GRADUATE STUDIES COLLEGE OF NATURA SCIENCES DEPARTMENT OF STATISTICS STATISTICAL ANALYSIS OF SPATIAL DISTRIBUTION OF MALARIA IN WEST SHOA ZONE, ETHIOPIA BY MITIKU MOSISSA AYANA A THESIS SUBMITTED TO THE SCHOOL OF GRADUATE STUDIES OF ADDISA ABABA UNIVERSITY IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF SCIENCE IN STATISTICS MAY, 2011 ADDISA ABABA, ETHIOPIA Addis Ababa University School of Graduate Studies Department of Statistics Title of Thesis: Statistical Analysis of Spatial Distribution of Malaria in West Shoa Zone, Ethiopia By Mitiku Mosissa Ayana Approved by the Board of Examiners: _____________________________ ……………… Department Head Signature _____________________________ ………………. Examiner Signature _____________________________ ……………… Examiner Signature CONTENTS Page Acronyms--------------------------------------------------------------------------------------------iv Acknowledgments----------------------------------------------------------------------------------v Abstract----------------------------------------------------------------------------------------------vi CHAPTER 1: Introduction -----------------------------------------------------------1 1.1. Background of the study----------------------------------------------------------------------1 1.2. Use of Spatial autocorrelation-----------------------------------------------------------------4 1.3. Statement of the problem----------------------------------------------------------------------6 1.4. Objectives of the study-------------------------------------------------------------------------7 1.5. Significance of the study-----------------------------------------------------------------------7 1.6. Limitations of the study------------------------------------------------------------------------7 CHAPTER 2: REVIEW OF LITERATURE----------------------------------8 CHAPTER 3: DATA AND METHODOLOGY------------------------------13 3.1. Source of data ---------------------------------------------------------------------------------13 3.2 Study area ---------------------------------------------------------------------------------------13 3.3. Methodology of the study--------------------------------------------------------------------14 3.3.1. The Concept of Spatial Dependence------------------------------------------------14 3.3.2. Global and local measures of spatial autocorrelation------------------------------15 3.3.2.1. Global measures of spatial autocorrelation---------------------------------15 3.3.2.2. Local measures of spatial autocorrelation-----------------------------------22 3.3.3. Diagnostics for spatial dependence---------------------------------------------------26 3.3.4. Modeling spatial dependence---------------------------------------------------------30 CHAPTER 4: RESULTS AND DISCUSSION--------------------------------38 4.1. Spatial distribution of malaria incidence by woreda--------------------------------------38 4.2. Testing for spatial autocorrelation ----------------------------------------------------------39 4.2.1. Moran’s I and Geary’s C test statistic for global spatial autocorrelation--------40 4.2.2. Local Moran’s I test statistic for local spatial autocorrelation-------------------42 i * 4.2.3. Local Gi test for spatial autocorrelation--------------------------------------------45 4.3. Diagnostics for spatial dependence ---------------------------------------------------------48 4.4. Fitting Spatial Autoregressive Model-------------------------------------------------------49 4.5. Normality test for residuals------------------------------------------------------------------53 4.6. Summary ---------------------------------------------------------------------------------------54 CHAPTER 5: CONCLUSIONS AND RECOMMENDATIONS---------55 5.1. Conclusions ------------------------------------------------------------------------------------55 5.2. Recommendations-----------------------------------------------------------------------------55 LIST OF TABLES Table 4.1: Results of Global Moran’s I and Geary’s C Statistics ----------------------------41 Table 4.2: Results of Local Moran’s I Test-----------------------------------------------------43 * Table 4.3: Results of Local Gi Test--------------------------------------------------------------46 Table 4.4: Diagnostics for Spatial Dependence ------------------------------------------------48 Table 4.5: Results of Spatial Lag Model Estimation-------------------------------------------51 Table 4.6: Summary Output of Regression Diagnostics for Spatial Lag Model-----------52 Table 4.7: Normality Test of Residuals----------------------------------------------------------53 LIST OF FIGURES Figure 3.1: Contiguity case of representation of spatial weights matrix --------------------18 Figure 3.2: Moran’s Scatter Plot------------------------------------------------------------------22 Figure 4.1: Spatial Distribution of the Malaria Incidence rate in West Shoa Zone--------39 Figure 4.2: Global Moran’s I Scatter Plot for Malaria Incidence----------------------------42 Figure 4.3: Local Moran’s I Scatter Plot for Malaria Incidence------------------------------44 * Figure 4.4: Local Gi Clustering Map of Malaria Incidence in West Shoa Zone, Ethiopia------------------------------------------------------------------------47 REFERENCES------------------------------------------------------------------------------------56 ii APPENDIX-----------------------------------------------------------------------------------------60 LIST OF TABLES AND FIGURES Figure A: Moran’s Scatter Plot Based on Neighborhood-------------------------------------60 Figure B: Moran’s Scatter Plot Based on Threshold Distance--------------------------------61 Figure C: Moran’s Scatter Plot Based on K-nearest Neighbors------------------------------61 Figure D: Normal Plot-----------------------------------------------------------------------------62 Table 1: Diagnostic for Multicollinearity--------------------------------------------------------62 Table 2: Malaria Incidence per 1000 people in each Woreda in West Shoa Zone, Ethiopia----------------------------------------------------------------------------------63 Table 3: Spatial Weighted Matrix W for Neighboring Relation among Woreda in West Shoa Zone, Ethiopia------------------------------------------------------------64 Table 4: Results of Maximum Likelihood Estimation (spatial lag model)------------------65 iii ACRONYMS CSA Central Statistical Agency FHOM Federal Ministry of Health ITN Insecticide treated nets IRS Indoor residual insecticide spraying LLINs Long-lasting insecticide treated nets OLS Ordinary Least Squares LM Lagrange Multiplier RLM Robust Langrage Multiplier VIF Variance inflation factor WHO World Health Organization iv ACKNOWLEDGMENTS First, and foremost, I express deepest gratitude to Dr. Butte Gotu, my advisor for his unlimited constructive advice, suggestions, ideas and comments. My thanks also to Central Statistical Agency and West Shoa Zone Health Bureau for providing me with the data for this thesis. Grateful acknowledgement is also expressed to the Department of Statistics, Addis Ababa University for kind assistance in many ways. Furthermore, I want to thank all my friends, my family members and others who have provided me a great help and moral support directly and indirectly contributed to wards the completion of this study. v ABSTRACT Malaria is a major cause of illness and death in large parts of the developing world, especially in Africa. Accurate estimates of malaria distribution are required for planning, implementation and evaluation of malaria control programs. The main objective of this study is to examine spatial patterns of malaria distribution in West Shoa zone, Oromia Region, Ethiopia. Malaria incidence data for 2009 from all health centers of the zone, population size and meteorological data were used. The statistical methods used include global and local measures of spatial autocorrelation as well as spatial autoregressive model. The results of this study indicate that malaria incidence varies according to geographical location, with eco-climatic condition and showing significant positive spatial autocorrelation. Significant local clustering of malaria incidence occurs between pairs of neighboring districts (known as Woredas). Malaria incidence was higher in the western part of the zone and lower in the eastern part of the zone. The results of spatial lag model indicate a significant relationship between malaria incidence and meteorological variables (mid-land zone, hot zone, rainfall, minimum temperature and maximum temperature). vi Chapter One Introduction 1.1 Background of the Study Malaria is the most common tropical disease, remaining widespread throughout the tropical and subtropical regions, including parts of Africa, Asia and America. It is a major cause of illness and death in large area of the developing world, especially Africa. According to the World Health Organization report (WHO, 2008), at the end of 2007 there were 109 malaria endemic countries and 3.3 billion people were at the risk of malaria. Malaria causes at least 300 million and possibly as many as 500 million cases of acute illness each year, which result in 1to 3 million deaths each year. Ninety percent of deaths occur in sub-Sahara Africa. The majority of these deaths are among children less than five years of age and pregnant women. These estimates are not reliable because of inadequate malaria case reporting in most endemic
Load more

Recommended publications
  • Districts of Ethiopia
    Region District or Woredas Zone Remarks Afar Region Argobba Special Woreda -- Independent district/woredas Afar Region Afambo Zone 1 (Awsi Rasu) Afar Region Asayita Zone 1 (Awsi Rasu) Afar Region Chifra Zone 1 (Awsi Rasu) Afar Region Dubti Zone 1 (Awsi Rasu) Afar Region Elidar Zone 1 (Awsi Rasu) Afar Region Kori Zone 1 (Awsi Rasu) Afar Region Mille Zone 1 (Awsi Rasu) Afar Region Abala Zone 2 (Kilbet Rasu) Afar Region Afdera Zone 2 (Kilbet Rasu) Afar Region Berhale Zone 2 (Kilbet Rasu) Afar Region Dallol Zone 2 (Kilbet Rasu) Afar Region Erebti Zone 2 (Kilbet Rasu) Afar Region Koneba Zone 2 (Kilbet Rasu) Afar Region Megale Zone 2 (Kilbet Rasu) Afar Region Amibara Zone 3 (Gabi Rasu) Afar Region Awash Fentale Zone 3 (Gabi Rasu) Afar Region Bure Mudaytu Zone 3 (Gabi Rasu) Afar Region Dulecha Zone 3 (Gabi Rasu) Afar Region Gewane Zone 3 (Gabi Rasu) Afar Region Aura Zone 4 (Fantena Rasu) Afar Region Ewa Zone 4 (Fantena Rasu) Afar Region Gulina Zone 4 (Fantena Rasu) Afar Region Teru Zone 4 (Fantena Rasu) Afar Region Yalo Zone 4 (Fantena Rasu) Afar Region Dalifage (formerly known as Artuma) Zone 5 (Hari Rasu) Afar Region Dewe Zone 5 (Hari Rasu) Afar Region Hadele Ele (formerly known as Fursi) Zone 5 (Hari Rasu) Afar Region Simurobi Gele'alo Zone 5 (Hari Rasu) Afar Region Telalak Zone 5 (Hari Rasu) Amhara Region Achefer -- Defunct district/woredas Amhara Region Angolalla Terana Asagirt -- Defunct district/woredas Amhara Region Artuma Fursina Jile -- Defunct district/woredas Amhara Region Banja -- Defunct district/woredas Amhara Region Belessa --
    [Show full text]
  • Thesis on Cattle Marketing
    SAINT MARY’S UNIVERSITY INSTITUTE OF AGRICULTURE AND DEVELOPMENT STUDIES GROSS MARGIN ANALYSIS OF CATTLE MARKETING IN WEST SHOA ZONE: A CASE STUDY OF GINCHI LIVESTOCK MARKET BY DEJENE TAKELE GEBISSA JULY, 2014 ADDIS ABABA, ETHIOPIA 1 GROSS MARGIN ANALYSIS OF CATTLE MARKETING IN WEST SHOA ZONE: A CASE STUDY OF GINCHI LIVESTOCK MARKET A THESIS SUBMITTED TO, SAINT MARY’S UNIVERSITY INSTITUTE OF AGRICULTURE AND DEVELOPMENT STUDIES IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF MASTER OF AGRICULTURAL ECONOMICS BY DEJENE TAKELE GEBISSA JULY, 2014 ADDIS ABABA, ETHIOPIA i DECLARATION I declare that this thesis entitled “Gross Margin Analysis of Cattle Marketing in West Shoa Zone: The Case of Ginchi Livestock Market” is my original work and has submitted for the partial fulfillment of MSc. Degree in Agricultural Economics. The study has not been presented for a degree fulfillment in any university and that all sources of data used for the thesis have been duly acknowledged. Name: Dejene Takele Gebissa Signature: ___________ Date: July, 2014 ii ENDORSEMENT As thesis research advisor, I hereby certify that I have read and evaluated this thesis prepared, under my guidance, by Dejene Takele entitled “Gross Margin Analysis of Cattle Marketing in West Shoa Zone: A Case Study of Ginchi Livestock Market.” I recommend that it be submitted as fulfilling the thesis requirement. ______________________ ______________________ Date: July, 2014 Advisor Signature iii EXAM APPROVAL SHEET SAINT MARY’S UNIVERSITY INSTITUTE OF AGRICULTURE AND DEVELOPMENT STUDIES As member of the Board of Examiners of the M.Sc Thesis Open Defense, we certify that we have read and evaluated the Thesis prepared by Dejene Takele and examined the candidate.
    [Show full text]
  • Determinants of Dairy Product Market Participation of the Rural Households
    ness & Fi si na u n c B Gemeda et al, J Bus Fin Aff 2018, 7:4 i f a o l l A a Journal of f DOI: 10.4172/2167-0234.1000362 f n a r i r u s o J ISSN: 2167-0234 Business & Financial Affairs Research Article Open Access Determinants of Dairy Product Market Participation of the Rural Households’ The Case of Adaberga District in West Shewa Zone of Oromia National Regional State, Ethiopia Dirriba Idahe Gemeda1, Fikiru Temesgen Geleta2 and Solomon Amsalu Gesese3 1Department of Agricultural Economics, College of Agriculture and Veterinary Sciences, Ambo University, Ethiopia 2Department of Agribusiness and Value Chain Management, College of Agriculture and Veterinary Sciences, Ambo University, Ethiopia Abstract Ethiopia is believed to have the largest Livestock population in Africa. Dairy has been identified as a priority area for the Ethiopian government, which aims to increase Ethiopian milk production at an average annual growth rate of 15.5% during the GTP II period (2015-2020), from 5,304 million litters to 9,418 million litters. This study was carried out to assess determinants of dairy product market participation of the rural households in the case of Adaberga district in West Shewa zone of Oromia national regional state, Ethiopia. The study took a random sample of 120 dairy producer households by using multi-stage sampling procedure and employing a probability proportional to sample size sampling technique. For the individual producer, the decision to participate or not to participate in dairy production was formulated as binary choice probit model to identify factors that determine dairy product market participation.
    [Show full text]
  • Prioritization of Shelter/NFI Needs
    Prioritization of Shelter/NFI needs Date: 31st May 2018 Shelter and NFI Needs As of 18 May 2018, the overall number of displaced people is 345,000 households. This figure is based on DTM round 10, partner’s assessments, government requests, as well as the total of HH supported since July 2017. The S/NFI updated its prioritisation in early May and SNFI Cluster partners agreed on several criteria to guide prioritisation which include: - 1) type of emergency, 2) duration of displacement, and 3) sub-standard shelter conditions including IDPS hosted in collective centres and open-air sites and 4) % of vulnerable HH at IDP sites. Thresholds for the criteria were also agreed and in the subsequent analysis the cluster identified 193 IDP hosting woredas mostly in Oromia and Somali regions, as well as Tigray, Gambella and Addis Ababa municipality. A total of 261,830 HH are in need of urgent shelter and NFI assistance. At present the Cluster has a total of 57,000 kits in stocks and pipeline. The Cluster requires urgent funding to address the needs of 204,830 HHs that are living in desperate displacement conditions across the country. This caseload is predicted to increase as the flooding continues in the coming months. Shelter and NFI Priority Activities In terms of priority activities, the SNFI Cluster is in need of ES/NFI support for 140,259 HH displaced mainly due to flood and conflict under Pillar 2, primarily in Oromia and Somali Regions. In addition, the Shelter and NFI Cluster requires immediate funding for recovery activities to support 14,000 HH (8,000 rebuild and 6,000 repair) with transitional shelter support and shelter repair activities under Pillar 3.
    [Show full text]
  • Globalization: Global Politics and Culture (Msc)
    LAND GRAB IN ETHIOPIA: THE CASE OF KARUTURI AGRO PRODUCTS PLC IN BAKO TIBE, OROMIYA Dejene Nemomsa Aga Supervisor: Professor Lund Ragnhild Master Thesis Faculty of Social Sciences and Technology Management Department of Geography Globalization: Global Politics and Culture (MSc). May 2014, Trondheim, Norway Globalization: Global Politics and Culture (M.Sc) Declaration I, the undersigned, declare that this thesis is my original work and all materials used as a source are duly acknowledged. Name:........................ Dejene Nemomsa Aga Date:……………........... 23 May, 2014 Dejene Nemomsa Aga Page i Globalization: Global Politics and Culture (M.Sc) Dedication I dedicate my master thesis work to anti-land grabbing protesters of Oromo Students and People, who were recently killed while protesting the implementation of ‘Integrated Development Master Plan of the Capital City of the country, Finfinne’, which planned to displace more than one million indigenous Oromo People from their ancestral land. 23 May, 2014 ii Dejene Nemomsa Aga Globalization: Global Politics and Culture (M.Sc) Acknowledgements Firsts, I would like to thank the almighty God. Next, my special thanks go to my advisor Professor Ragnhild Lund, for her guidance and detailed constructive comments that strengthened the quality of this thesis. Professor’s countless hours of reflecting, reading, encouraging, and patience throughout the entire process of the research is unforgettable. I would like to thank Norwegian University of Science and Technology for accepting me as a Quota Scheme Student to exchange knowledge with students who came from across the globe and Norwegian State Educational Loan Fund for covering all my financial expenses during my stay. My special thanks go to department of Geography, and Globalization: Global Politics and Culture program coordinators, Anette Knutsen for her regular meetings and advice in the research processes.
    [Show full text]
  • ETHIOPIA Selfhelpafrica.Org 2020-21 1 2020-21 Alemnesh Tereda, 28, and Marsenesh Lenina, 29, Injaffo Multi Barley Coop, Gumer
    ETHIOPIA selfhelpafrica.org 2020-21 1 2020-21 Alemnesh Tereda, 28, and Marsenesh Lenina, 29, Injaffo Multi barley Coop, Gumer caling up agricultural production, improving nutrition Last year, the organisation was involved in implementing security, developing new enterprise and market close to a dozen development projects, all of which Sopportunities for farmers, strengthening community- are being undertaken in collaboration with local and/or based seed production and building climate resilience, are international partners. all key areas of Self Help Africa’s work in Ethiopia. ETHIOPIA PROJECT KEY Scaling up RuSACCOs Strengthening & Scaling up of rehabilitaion of degraded lands and enhancement of livelihoods in Lake Ziway catchment ERITREA Feed the Future Gondar Dairy for Development Stronger Together: Linking Primary Seed and Seep Cooperative Union Addis Ababa Climate-Smart Agriculture SOMALILAND Capacity Building of Farmer Butajira Training Centers Unleashing the productive ETHIOPIA capacity of poor people through Graduation Approach in Ethiopia Integrated Community Development SOMALIA Livelihood Enhancement: Working Inclusively for Transformation KENYA 2 Implementing Programme Programme Donor Total Budget Time Frame Partner Area Climate-Smart Irish Aid € 806,695 2015 SOS Sahel, SNNP region 01 Agriculture (CSA) Farm Africa, 2019 Vita MF: Scaling Up Irish League of € 420,000 2020 Zonal Departments of N/Shewa Zone of 02 Rural Savings and Credit international Finance & Economic Amhara, N/Shewa Credit Cooperatives Development 2022 Cooperation
    [Show full text]
  • Oromia Region Administrative Map(As of 27 March 2013)
    ETHIOPIA: Oromia Region Administrative Map (as of 27 March 2013) Amhara Gundo Meskel ! Amuru Dera Kelo ! Agemsa BENISHANGUL ! Jangir Ibantu ! ! Filikilik Hidabu GUMUZ Kiremu ! ! Wara AMHARA Haro ! Obera Jarte Gosha Dire ! ! Abote ! Tsiyon Jars!o ! Ejere Limu Ayana ! Kiremu Alibo ! Jardega Hose Tulu Miki Haro ! ! Kokofe Ababo Mana Mendi ! Gebre ! Gida ! Guracha ! ! Degem AFAR ! Gelila SomHbo oro Abay ! ! Sibu Kiltu Kewo Kere ! Biriti Degem DIRE DAWA Ayana ! ! Fiche Benguwa Chomen Dobi Abuna Ali ! K! ara ! Kuyu Debre Tsige ! Toba Guduru Dedu ! Doro ! ! Achane G/Be!ret Minare Debre ! Mendida Shambu Daleti ! Libanos Weberi Abe Chulute! Jemo ! Abichuna Kombolcha West Limu Hor!o ! Meta Yaya Gota Dongoro Kombolcha Ginde Kachisi Lefo ! Muke Turi Melka Chinaksen ! Gne'a ! N!ejo Fincha!-a Kembolcha R!obi ! Adda Gulele Rafu Jarso ! ! ! Wuchale ! Nopa ! Beret Mekoda Muger ! ! Wellega Nejo ! Goro Kulubi ! ! Funyan Debeka Boji Shikute Berga Jida ! Kombolcha Kober Guto Guduru ! !Duber Water Kersa Haro Jarso ! ! Debra ! ! Bira Gudetu ! Bila Seyo Chobi Kembibit Gutu Che!lenko ! ! Welenkombi Gorfo ! ! Begi Jarso Dirmeji Gida Bila Jimma ! Ketket Mulo ! Kersa Maya Bila Gola ! ! ! Sheno ! Kobo Alem Kondole ! ! Bicho ! Deder Gursum Muklemi Hena Sibu ! Chancho Wenoda ! Mieso Doba Kurfa Maya Beg!i Deboko ! Rare Mida ! Goja Shino Inchini Sululta Aleltu Babile Jimma Mulo ! Meta Guliso Golo Sire Hunde! Deder Chele ! Tobi Lalo ! Mekenejo Bitile ! Kegn Aleltu ! Tulo ! Harawacha ! ! ! ! Rob G! obu Genete ! Ifata Jeldu Lafto Girawa ! Gawo Inango ! Sendafa Mieso Hirna
    [Show full text]
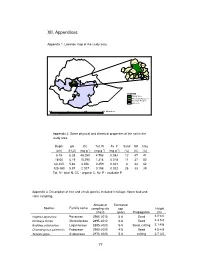
  • XII. Appendices
    XII. Appendices Appendix 1. Location map of the study area. Ginde Beret Meta Robi Adaa Berga Study Area Ejere Bako Tibe Welmera Chelia Ambo Tikur Dawo Illu Alem Gana Da no Wenchi Becho Nonno Tolle Ameya Welisona Gorro Kokir Kersana Kondelt Gin de B e re t Met a Ro bi Ad aa Be rga Study Ar ea Ejere We lme ra Ba ko T ibe Ch el i a Amb o YA#ddis A baba Ti ku r Da wo Il lu Al em Ga na Da no We nch i No nn o Ame ya Be ch o To le We li so na Ke rsan a Gorro Ko nd elt LEGEND Study Area West Shewa Zone Oromya Region Ethiopia 400 0 400 800 Kilometers Appendix 2. Some physical and chemical properties of the soil in the study area. Depth pH OC Tot. N Av. P Sand Silt Clay -1 -1 -1 (cm) (H2O) (mg g ) (mg g ) (mg g ) (%) (%) (%) 0-18 6.28 48.280 4.796 0.083 12 47 41 18-60 6.19 15.290 1.316 0.018 11 37 52 60-125 5.66 4.356 0.459 0.021 4 34 62 125-160 5.97 2.027 0.198 0.022 28 33 39 Tot. N - total N, OC - organic C, Av. P - available P Appendix 3. Description of tree and shrub species included in foliage, flower bud and stem sampling. Altitude of Estimated Species Familly name sampling site age Height (masl) (year) Propagation (m) Hagenia abyssinica Rosaceae 2960-3015 5-8 Seed 4.0-4.6 Dombeya torrida Sterculiaceae 2895-3010 6-8 Seed 4.3-5.0 Buddleja polystachya Loganiaceae 2895-3020 5-9 Seed, cutting 3.1-4.6 Chamaecytisus palmensis Fabaceae 2900-3000 4-5 Seed 4.5-4.9 Senecio gigas Asteraceae 2970-3020 5-8 cutting 2.7-3.5 77 Appendix 4.
    [Show full text]
  • Somali Region
    Food Supply Prospects FOR THE SECOND HALF OF YEAR 2013 ______________________________________________________________________________ Disaster Risk Management and Food Security Sector (DRMFSS) Ministry of Agriculture (MoA) September, 2013 Addis Ababa, Ethiopia TABLE OF CONTENTS GLOSSARY OF LOCAL NAMES .................................................................. 1 ACRONYMS ............................................................................................. 2 EXCUTIVE SUMMARY .............................................................................. 3 INTRODUCTION ....................................................................................... 7 REGIONAL SUMMARY OF FOOD SUPPLY PROSPECT ............................. 11 SOMALI .............................................................................................. 11 OROMIA ............................................................................................. 16 TIGRAY ............................................................................................... 22 AMHARA ............................................................................................ 25 AFAR .................................................................................................. 28 SNNP .................................................................................................. 32 Annex – 1: NEEDY POPULATION AND FOOD REQUIREMENT BY WOREDA (Second half of 2013) ............................................................................ 35 0 | P a g e GLOSSARY
    [Show full text]
  • Ethiopia: Administrative Map (August 2017)
    Ethiopia: Administrative map (August 2017) ERITREA National capital P Erob Tahtay Adiyabo Regional capital Gulomekeda Laelay Adiyabo Mereb Leke Ahferom Red Sea Humera Adigrat ! ! Dalul ! Adwa Ganta Afeshum Aksum Saesie Tsaedaemba Shire Indasilase ! Zonal Capital ! North West TigrayTahtay KoraroTahtay Maychew Eastern Tigray Kafta Humera Laelay Maychew Werei Leke TIGRAY Asgede Tsimbila Central Tigray Hawzen Medebay Zana Koneba Naeder Adet Berahile Region boundary Atsbi Wenberta Western Tigray Kelete Awelallo Welkait Kola Temben Tselemti Degua Temben Mekele Zone boundary Tanqua Abergele P Zone 2 (Kilbet Rasu) Tsegede Tselemt Mekele Town Special Enderta Afdera Addi Arekay South East Ab Ala Tsegede Mirab Armacho Beyeda Woreda boundary Debark Erebti SUDAN Hintalo Wejirat Saharti Samre Tach Armacho Abergele Sanja ! Dabat Janamora Megale Bidu Alaje Sahla Addis Ababa Ziquala Maychew ! Wegera Metema Lay Armacho Wag Himra Endamehoni Raya Azebo North Gondar Gonder ! Sekota Teru Afar Chilga Southern Tigray Gonder City Adm. Yalo East Belesa Ofla West Belesa Kurri Dehana Dembia Gonder Zuria Alamata Gaz Gibla Zone 4 (Fantana Rasu ) Elidar Amhara Gelegu Quara ! Takusa Ebenat Gulina Bugna Awra Libo Kemkem Kobo Gidan Lasta Benishangul Gumuz North Wello AFAR Alfa Zone 1(Awsi Rasu) Debre Tabor Ewa ! Fogera Farta Lay Gayint Semera Meket Guba Lafto DPubti DJIBOUTI Jawi South Gondar Dire Dawa Semen Achefer East Esite Chifra Bahir Dar Wadla Delanta Habru Asayita P Tach Gayint ! Bahir Dar City Adm. Aysaita Guba AMHARA Dera Ambasel Debub Achefer Bahirdar Zuria Dawunt Worebabu Gambela Dangura West Esite Gulf of Aden Mecha Adaa'r Mile Pawe Special Simada Thehulederie Kutaber Dangila Yilmana Densa Afambo Mekdela Tenta Awi Dessie Bati Hulet Ej Enese ! Hareri Sayint Dessie City Adm.
    [Show full text]
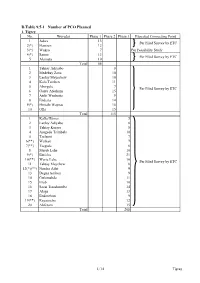
  • D.Table 9.5-1 Number of PCO Planned 1
    D.Table 9.5-1 Number of PCO Planned 1. Tigrey No. Woredas Phase 1 Phase 2 Phase 3 Expected Connecting Point 1 Adwa 13 Per Filed Survey by ETC 2(*) Hawzen 12 3(*) Wukro 7 Per Feasibility Study 4(*) Samre 13 Per Filed Survey by ETC 5 Alamata 10 Total 55 1 Tahtay Adiyabo 8 2 Medebay Zana 10 3 Laelay Mayechew 10 4 Kola Temben 11 5 Abergele 7 Per Filed Survey by ETC 6 Ganta Afeshum 15 7 Atsbi Wenberta 9 8 Enderta 14 9(*) Hintalo Wajirat 16 10 Ofla 15 Total 115 1 Kafta Humer 5 2 Laelay Adiyabo 8 3 Tahtay Koraro 8 4 Asegede Tsimbela 10 5 Tselemti 7 6(**) Welkait 7 7(**) Tsegede 6 8 Mereb Lehe 10 9(*) Enticho 21 10(**) Werie Lehe 16 Per Filed Survey by ETC 11 Tahtay Maychew 8 12(*)(**) Naeder Adet 9 13 Degua temben 9 14 Gulomahda 11 15 Erob 10 16 Saesi Tsaedaemba 14 17 Alage 13 18 Endmehoni 9 19(**) Rayaazebo 12 20 Ahferom 15 Total 208 1/14 Tigrey D.Table 9.5-1 Number of PCO Planned 2. Affar No. Woredas Phase 1 Phase 2 Phase 3 Expected Connecting Point 1 Ayisaita 3 2 Dubti 5 Per Filed Survey by ETC 3 Chifra 2 Total 10 1(*) Mile 1 2(*) Elidar 1 3 Koneba 4 4 Berahle 4 Per Filed Survey by ETC 5 Amibara 5 6 Gewane 1 7 Ewa 1 8 Dewele 1 Total 18 1 Ere Bti 1 2 Abala 2 3 Megale 1 4 Dalul 4 5 Afdera 1 6 Awash Fentale 3 7 Dulecha 1 8 Bure Mudaytu 1 Per Filed Survey by ETC 9 Arboba Special Woreda 1 10 Aura 1 11 Teru 1 12 Yalo 1 13 Gulina 1 14 Telalak 1 15 Simurobi 1 Total 21 2/14 Affar D.Table 9.5-1 Number of PCO Planned 3.
    [Show full text]
  • Seroprevalence and Associated Risk Factors of Foot and Mouth Disease in Cattle in West Shewa Zone, Ethiopia
    Hindawi Veterinary Medicine International Volume 2020, Article ID 6821809, 6 pages https://doi.org/10.1155/2020/6821809 Research Article Seroprevalence and Associated Risk Factors of Foot and Mouth Disease in Cattle in West Shewa Zone, Ethiopia Beyan Ahmed,1 Lencho Megersa ,2 Getachew Mulatu ,2 Mohammed Siraj,2 and Gelma Boneya2 1Department of Veterinary Science, College of Agriculture and Veterinary Science, Ambo University, P.O. Box 19, Ambo, Ethiopia 2Department of Veterinary Laboratory Technology, College of Agriculture and Veterinary Sciences, Ambo University, P.O. Box 19, Ambo, Ethiopia Correspondence should be addressed to Lencho Megersa; [email protected] Received 7 November 2019; Revised 19 February 2020; Accepted 7 March 2020; Published 31 March 2020 Academic Editor: Annamaria Pratelli Copyright © 2020 Beyan Ahmed et al. (is is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. Foot and mouth disease (FMD) is a highly contagious viral disease of cloven-hoofed animals and one of the endemic diseases in Ethiopia. (e study was aimed to estimate the seroprevalence and to assess associated risk factors of foot and mouth disease seroprevalence in West Shewa Zone. A total of 384 sera samples were collected from randomly selected cattle and tested using ELISA for antibodies against nonstructural proteins of foot and mouth disease viruses based on IDEXX FMD Multispecies Ab Test (IDEXX Laboratories Inc, USA). (e seroprevalence of foot and mouth disease in West Shewa Zone was found to be 40.4% (95% CI: 35.46–45.27) at an animal and 74.7% (95% CI: 65.58–83.85) at the herd level.
    [Show full text]