DOCSLIB.ORG

Use of Photometric Stereo for the Accurate Modelling of Three

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Use of Photometric Stereo for the Accurate Modelling of Three Use of Photometric Stereo for the Accurate Modelling of Three-Dimensional Skin Microrelief Ali Sohaib A thesis submitted in partial fulfilment of the requirements of the University of the West of England, Bristol for the degree of Doctor of Philosophy Faculty of the Environment and Technology University of the West of England, Bristol October 2013 Abstract The largest organ of human body - ”skin” is a multilayered organ with complex reflectance properties that not only vary with the direction of illumination but also with the wavelength of light. The complex Three Dimensional (3D) structure and optical properties of human skin makes it very difficult for techniques like Pho- tometric stereo to accurately recover its 3D shape. One problem in particular concerns the presence of interreflections at concave regions of the skin surface topography. Common features such as wrinkles, moles, lesions, burns and sur- gical scars can appear as elevated skin area or as indentations in the skin sur- face, and usually have a different colour when compared to the surrounding skin. These differences in colour and the degree of concavity determine the amount of interreflection present and hence significantly affect the overall recovery of the 3D topography of the skin. This thesis explores the use of varying incident light wavelength in the visible spectrum to improve the recovered topography of human skin. New algorithms were developed and implemented to minimise the effects of interreflections and an accuracy assessment of using wavelengths in the visible spectrum was carried out for Caucasian, Asian and African American skin types. The results demonstrate that white light is not ideal for imaging skin relief and also illustrate the differences in recovered skin topography due to a non-diffuse Bidi- rectional Reflectance Distribution Function (BRDF) for each colour illumination used. In addition to the complication caused by interreflections, the translucency of skin allows light to scatter within the skin. This confutes the assumption asso- ciated with photometric stereo that - light incident on a particular patch of the skin is reflected at the same point. This issue is taken care of by incorporating polarisation information with photometric stereo to improve the 3D skin shape recovery. The experiments conducted show improvement in the recovered skin ii topography when specular reflected light was used instead of the multiply sub- surface scattered diffuse light emanating from within the skin. The results also show an increase in polarised reflected light as the albedo of the skin decreases with wavelength in the visible spectrum, while darker skin tend to reflect more polarised light than lighter skin at similar wavelengths in the visible spectrum. These characteristics of human skin have not been investigated before and are important additions to the current state of the art in skin optics. iii Acknowledgements This research project would not have been possible without the support of many people. Foremost, I would like to express my gratitude to my principal supervisor Professor Melvyn Smith for his support and thoughtful guidance during my Ph.D study. In addition, I would like to acknowledge my supervisory team Dr Lyndon Smith, Dr Abdul Farooq and Mr Robb Warr for their invaluable assistance in the completion of this thesis and for providing constructive feedback on my research throughout. I would also like to express my gartitude to Dr Jeffrey Bamber and Nigel Bush at the Institute of Cancer Research, Sutton, UK for allowing me to use the PRI- MOS device. Furthermore, I would like to take this opportunity to thank all my colleagues at the Centre for Machine Vision, UWE, especially Laurence Broad- bent for his help with the CAD drawings of the numerous parts made during my PhD and Jahanzeb Ahmed for his help with the PovRay software. I would also like to thank Christopher Hart for the rapid prototyping of various parts used in the experiments. I am also thankful to all the participants who agreed to take part in this re- search study. Finally, I would like to express my deepest gratitude to my family: Mum, Dad, my brother and sister and my wife for their endless patience, support and encour- agement when it was most required. iv This work is dedicated to my family, especially Mum and Dad. v Contents 1 Introduction 1 1.1 Original Contributions . 3 1.2 Applications of Research . 5 1.3 Thesis Outline . 7 2 Literature survey 9 2.1 Review of Wrinkle Grading Scales . 9 2.2 Skin Anatomy . 10 2.3 Optical Properties of Skin . 14 2.4 Wrinkle Grading . 17 2.4.1 Photographic Scales . 18 2.4.2 Conditions for Analysis . 21 2.4.3 Wrinkle Grading Systems Discussion . 21 2.5 Review of 3D Imaging Techniques . 23 2.5.1 Replica Technique . 23 2.5.2 Mechanical Microscopy . 24 2.5.3 Laser Triangulation . 25 2.5.4 Fringe Projection . 26 2.5.5 Light Transmission . 26 2.5.6 Photometric Stereo . 27 2.6 Simulation Based Analysis of Skin Topography . 30 vi 2.7 Parameters Commonly Used to Characterise Surfaces . 30 2.8 Discussion . 33 3 Photometric Stereo and Reflectance Models 35 3.1 Reflectance Models . 38 3.1.1 Lambertian Model . 39 3.1.2 Phong and Blinn-Phong Model . 40 3.1.3 Oren Nayer Model . 42 3.1.4 Torrance-Sparrow Model . 43 3.1.5 Ward Model . 46 3.2 Discussion . 47 4 Interreflection Modelling of Skin 49 4.1 Literature Survey . 51 4.2 Skin Optical Characteristics . 55 4.3 Multispectral Reflectance of Skin . 57 4.4 BRDF of Skin as a Function of Wavelength . 58 4.5 Materials and Methods . 59 4.5.1 Photometric Stereo Setup and Acquisition . 59 4.5.2 Camera Calibration . 61 4.6 Segmentation Based Method . 64 4.6.1 Skin Replica and Ground Truth . 64 4.6.2 Error Analysis . 65 4.6.3 Algorithm for Improved Depth Estimate . 67 4.6.4 Skin Roughness Analysis . 70 4.7 Gradient Spread Method . 75 4.7.1 Skin Replica and Ground Truth . 75 4.7.2 Error Analysis . 76 4.7.3 Surface Normal Mapping in Gradient Space . 80 vii 4.7.4 Validation . 84 4.8 Discussion . 85 4.9 Conclusion . 87 5 Shape from Polarisation 90 5.1 Literature Survey . 92 5.2 Polarisation Based Separation of Diffuse and Specular components 94 5.3 Umov Effect . 96 5.3.1 Setup for Umov Effect . 97 5.4 Shape from Specular and Diffuse Reflection . 100 5.5 Synthetic Image Analysis . 101 5.6 Algorithm . 104 5.7 Real Surface Analysis . 105 5.8 Skin Microrelief Analysis . 107 5.9 Discussion . 110 6 Conclusions, Limitations and Future Work 112 6.1 Summary of Contributions . 112 6.2 Future Work . 116 Glossary 139 List of Symbols 143 Appendices 146 A Datasheets 146 A.1 LED Datasheet . 147 A.2 Camera Datasheet . 160 A.3 Camera Datasheet . 163 A.4 Triband Filter Datasheet . 166 viii B Mathematical Derivations 168 B.1 Cross Product for Normal Vector Calculation . 168 B.2 Constraint calculation for diffuse component . 170 ix List of Figures 2.1 (a) Cross-sectional view of skin showing epidermis, dermis and appendage structures. (b) Cellular structure of epidermis . 12 2.2 Interaction of light with skin. 15 3.1 A graphical representation of facet. 37 3.2 Arrangement of incident, viewing, halfway and reflection vector. 40 4.1 The underestimation of concave shape from photometric stereo. 49 4.2 Multispectral reflectance of different skin types (NCSU skin reflectance data [1]). 57 4.3 (a) Schematics of the photometric stereo based 3D capture sys- tem. (b) The 3D skin macro and microrelief from the back of the hand acquired using the device. 60 4.4 (a) CCD spectral response. (b) Triband filter response. (c) Spectral response of the LEDs . 62 4.5 Cross-sectional view of the wrinkled region obtained from each colour light and the proposed algorithm. 66 4.6 (a) original image. (b) Segmented wrinkle line using watershed algorithm. 68 4.7 Comparison of algorithm with ground truth. 70 4.8 (Graphical representation of cube size variation ((a) - (c)) used for the calculation of Fractal dimension for a patch of skin. 74 x 4.9 (a) Forehead wrinkle directly imaged using photometric stereo de- vice. (b) Corresponding replica. (c) 3D reconstruction of skin im- ages taken in vivo............................ 76 4.10 (a) 2D Profiles obtained for the wrinkled region from each colour light and the proposed method (The wrinkle lies between 6-8mm length). (b)-(f) RMS error in height from red, green, blue, white light and the algorithm respectively (The dotted rectangular region points out the location of wrinkle). 78 4.11 (a) Over and underestimation of slope from each (R, G, B) light at the wrinkled region (valley). The mid region data value rise repre- sents lowest point of valley of wrinkle where slope changes sign. (b) Increased scale to show differences in slope from one side of valley. 79 4.12 Gradient map obtained from red and green light (The center cluster of a lighter shading represents the group of gradients from red light). 80 4.13 Movement of gradients from red light towards the green. The gradi- ent set is calculated in the region bounded between quadratic and linear fits. 81 5.1 The setup uses a rotating polariser in front of the camera and linear polarisers in front of RGBW LEDs. 97 5.2 1st row: Degree of polarisation (DOP) for red light, green and blue light for a Caucasian (European) Subject. 2nd row: Degree of po- larisation for red light, green and blue light for a Asian (Chinese) Subject. (The Image intensity represents the degree of polarisa- tion of light in the range 0 to 1) .
Load more

Recommended publications
  • Penile Circular Fasciocutaneous Flaps for Complex Anterior Urethral Strictures K.J
    18 Penile Circular Fasciocutaneous Flaps for Complex Anterior Urethral Strictures K.J. Carney, J.W. McAninch 18.1 Penile Fascial Anatomy – 146 18.2 Flap Anatomy – 148 18.3 Patient Selection – 148 18.4 Preoperative Preparation – 148 18.5 Patient Positioning – 148 18.6 Flap Harvest – 149 18.7 Stricture Exposure – 150 18.8 Anastomosis – 151 18.9 Postoperative Care – 152 References – 152 146 Chapter 18 · Penile Circular Fasciocutaneous Flaps for Complex Anterior Urethral Strictures Surgical reconstruction of complex anterior urethral stric- Buck’s fascia is a well-defined fascial layer that is close- tures, 2.5–6 cm long, frequently requires tissue-transfer ly adherent to the tunica albuginea. Despite this intimate techniques [1–8]. The most successful are full-thickness association, a definite plane of cleavage exists between the free grafts (genital skin, bladder mucosa, or buccal muco- two, permitting separation and mobilization. Buck’s fascia sa) or pedicle-based flaps that carry a skin island. Of acts as the supporting layer, providing the foundation the latter, the penile circular fasciocutaneous flap, first for the circular fasciocutaneous penile flap. Dorsally, the described by McAninch in 1993 [9], produces excel- deep dorsal vein, dorsal arteries, and dorsal nerves lie in a lent cosmetic and functional results [10]. It is ideal for groove just deep to the superficial lamina of Buck’s fascia. reconstruction of the distal (pendulous) urethra, where The circumflex vessels branch from the dorsal vasculature the decreased substance of the corpus spongiosum may and lie just deep to Buck’s fascia over the lateral aspect jeopardize graft viability.
    [Show full text]
  • The Biophysical Modeling of the Human Tegument
    International Research Journal of Pharmacy and Medical Sciences ISSN (Online): 2581-3277 The Biophysical Modeling of the Human Tegument Janos Vincze, Gabriella Vincze-Tiszay Health Human International Environment Foundation, Budapest, Hungary Email address: [email protected] Abstract— Sensory organs are parts of our body, which collect and transmit information to the central nervous system about the outside world, and about the internal condition of our body. The body collects information by millions of microscopic structures, the so-called receptor cells. These can be found in almost all parts of the body, skin, muscle, joints, internal organs, in the walls of blood-vessels and in specialized organs such as the eye or the inner ear. There are numerous types of receptor cells in the skin. Some of them register mechanical stress or pressure, others the position and displacement of sensory hairs. Different stimulation cause different sensations, such as pain, tickling, hard or light pressure, heat or cold. The nerve fibres connected to the receptor transform stimuli above threshold into sequence of actions potentials. We modelling the action potential in the mathematical equation. Although our current knowledge regarding the mechanisms of pain development is incomplete, a number of pain-related phenomena have been discovered, which bear importance from both pathobiophysical and clinical aspects. Skin is an important receptive field, due to the numerous and various terminations of the cutaneous analyser which informs the nervous centres on the proprieties and phenomena that the body gets in contact with. Keywords— human tegument, hand nail, action potential, pain reception. loosing the function of one or more analysers, reach a special I.
    [Show full text]
  • Introduction
    Tikrit University College of Dentistry .Human Anatomy 1st y د.ﺑﺎن إﺳﻤﺎﻋﯿﻞ Introduction Anatomy: Anatomy is the study of the structures of the body. Gross anatomy: deals with those structures that can be seen without a microscope. The anatomical position:For descriptive purposes the body is always imagined to be in the anatomical position, standing erect, arms by sides, palms of hands facing forwards. Terms: Median Sagittal Plane: This is a vertical plane passing through the center of the body, dividing it into equal right and left halves. A structure situated nearer to the median plane of the body than another is said to be medial to the other. Similarly, a structure that lies farther away from the median plane than another is said to be lateral to the other. 1 cden.tu.edu.iq Tikrit University College of Dentistry .Human Anatomy 1st y د.ﺑﺎن إﺳﻤﺎﻋﯿﻞ Coronal Planes: are imaginary vertical planes at right angles to the median plane. divides the body into anterior and posterior parts. Horizontal, or Transverse, Planes : These planes are at right angles to both the median and the coronal planes. Divides the body into superior and inferior. The terms anterior and posterior are used to indicate the front and back of the body, respectively. The terms proximal and distal describe the relative distances from the roots of the limbs; for example, the arm is proximal to the forearm and the hand is distal to the forearm. The terms superficial and deep represent the relative distances of structures from the surface of the body. The terms superior and inferior represent levels relatively high or low with reference to the upper and lower ends of the body.
    [Show full text]
  • Article in Press
    G Model FISH-4564; No. of Pages 11 ARTICLE IN PRESS Fisheries Research xxx (2016) xxx–xxx Contents lists available at ScienceDirect Fisheries Research journal homepage: www.elsevier.com/locate/fishres Full length article 3D-Xray-tomography of American lobster shell-structure. An overview Joseph G. Kunkel a,b,∗, Melissa Rosa b, Ali N. Bahadur c a University of Massachusetts, Amherst, MA 01003, United States b University of New England, Biddeford, ME 04005, United States c Bruker BioSpin Corp., Billerica, MA 01821, United States article info a b s t r a c t Article history: A total inventory of density defined objects of American lobster cuticle was obtained by using high res- Received 16 January 2016 olution 3D Xray tomography, micro-computed-tomography. Through this relatively unbiased sampling Received in revised form approach several new objects were discovered in intermolt cuticle of the lobster carapace. Using free and 13 September 2016 open-source software the outlines of density-defined objects were obtained and their locations in 3D Accepted 23 September 2016 space calculated allowing population parameters about these objects to be determined. Nearest neigh- Available online xxx bor distances between objects allowed interpretations of structural relationships of and between objects. Several organule types are recognized by their structural outlines and density signatures. A hierarchy of Keywords: Homarus americanus organule types and distribution suggests they develop during sequential molts. New objects (stalactites, American lobster Bouligand spirals, and basal granules) are described as mineral structures with well defined morpholog- MicroCT ical character, allowing them to be recognized by their descriptive names and distributions.
    [Show full text]
  • 467 1.Pdf (10.98Mb)
    Reduction of Biomechanical Models and Subject Specific Properties for Real-Time Simulation of Surgical Trocar Insertion By RAVI KUMAR CHANNA NAIK September 1, 2010 A thesis submitted to the Faculty of the Graduate School of The State University of New York at Buffalo in partial completion of the requirements for the degree of MASTER OF SCIENCE Department of Mechanical Engineering ACKNOWLEDGEMENTS I take this rare opportunity to thank one and all who have been the source of support, motivation and encouragement, both on the screen and tangible and behind the screen and intangible. I thank my academic research advisor Dr. Gary Dargush, committee members Dr. Andres Soom and Dr. Roger Mayne for all the support and guidance for my master’s thesis research and writing. I thank my family members, for their long and steady support and encouragement which gave me the strength and stability throughout the course my of study and research. I thank my peer friends, who have been very supportive, the source of recreations and a change in grave and stagnation periods and helped me to keep up my motivation and vigor in completing this thesis. Finally I thank God and associated holy company for giving me this opportunity to pursue my graduate studies at University at Buffalo and carry out this master’s research. ii ABSTRACT Trocar insertion is the first step in Laparoscopy, Thoracoscopy and most other micro surgery procedures. It is a difficult procedure to learn and practice because procedure is carried out almost entirely without any visual feedback of the organs underlying the tissues being punctured.
    [Show full text]
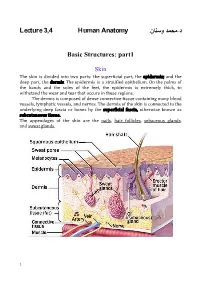
  • Lecture 3,4 Human Anatomy نﺎﻨﺴو دﻤﺤﻤ.د Basic Structures: Part1
    د.ﻤﺤﻤد وﺴﻨﺎن L ectur e 3,4 Human Anatomy Basic Structures: part1 Skin The skin is divided into two parts: the superficial part, the epidermis; and the deep part, the dermis. The epidermis is a stratified epithelium. On the palms of the hands and the soles of the feet, the epidermis is extremely thick, to withstand the wear and tear that occurs in these regions. The dermis is composed of dense connective tissue containing many blood vessels, lymphatic vessels, and nerves. The dermis of the skin is connected to the underlying deep fascia or bones by the superficial fascia, otherwise known as subcutaneous tissue. The appendages of the skin are the nails, hair follicles, sebaceous glands, and sweat glands. 1 Fasciae The fasciae of the body can be divided into two types— superficial and deep— and lie between the skin and the underlying muscles and bones. The superficial fascia, or subcutaneous tissue, is a mixture of loose areolar and adipose tissue that unites the dermis of the skin to the underlying deep fascia. The deep fascia is a membranous layer of connective tissue that invests the muscles and other deep structures. In the neck, it forms well-defined layers and in the thorax and abdomen, it is merely a thin film of areolar tissue covering the muscles and aponeuroses. Muscle The three types of muscle are skeletal, smooth, and cardiac. Skeletal Muscle Skeletal muscles produce the movements of the skeleton; they are sometimes called voluntary muscles and are made up of striped muscle fibers. A skeletal muscle has two or more attachments.
    [Show full text]
  • Human Anatomy - Sense Organs -Textbook
    ALINA MARIA ȘIȘU SORIN LUCIAN BOLINTINEANU Human Anatomy - Sense Organs -Textbook- Editura „Victor Babeş” TIMIŞOARA, 2021 MANUALE Alina Maria Șișu Associate Professor, MD,PhD, Department of Anatomy and Embryology, English Section, Medicine, First Year Victor Babeș University of Medicine and Pharmacy Timisoara Sorin Lucian Bolintineanu Full Professor, MD,PhD, Head of Department of Anatomy and Embryology, Victor Babeș University of Medicine and Pharmacy Timisoara 2 Editura „Victor Babeş” Piaţa Eftimie Murgu nr. 2, cam. 316, 300041 Timişoara Tel./ Fax 0256 495 210 e-mail: [email protected] www.umft.ro/editura Director general: Prof. univ. emerit dr. Dan V. Poenaru Referent ştiinţific: Conf. univ. dr. med. Liana Dehelean Colecţia: MANUALE Indicativ CNCSIS: 324 © 2021 Toate drepturile asupra acestei ediţii sunt rezervate. Reproducerea parţială sau integrală a textului, pe orice suport, fără acordul scris al autorilor este interzisă şi se va sancţiona conform legilor în vigoare. ISBN 978-606-786-232-4 3 Contents I. ORGAN OF THE SIGHT/ THE EYE (Organon Visus) * S. Bolintineanu .................................................................. 5 1. The fibrous tunic/layer (Tunica fibrosa oculi)............................................. 6 2. The vascular tunic (Tunica vasculosa oculi) ................................................ 8 3. The retina (Tunica interna) .......................................................................11 4. The refracting media ................................................................................13 5.
    [Show full text]
  • Anatomy of the Fascia
    2 ANATOMY OF THE FASCIA The superficial fascia The deep fascia • anatomy of the hypodermis: trunk • anatomy of the deep fascia: limbs < • anatomy of the hypodermis: limbs • anatomy of the deep fascia: trunk I U L ^ ANATOMY OF THE FASCIA I Superficial fascia Fig. 1.1. Schematic arrangement Adipose Retinaculum Ground of the fasciae in the human body. cell cutis superf. substance The hypodermis lies beneath the t Dermis dermis and it is formed by three Adipose layer layers of connective tissue. These aaaamao layers are often inappropriately Membranous layer called the superficial fascia. The Anatomy Anatomy of the fascia or superficial fascia hypodermis is formed by an adi­ Loose connect, tissue pose layer with the retinaculum Aponeurotic fascia cutis superficial^, a membranous Epimysial fascia layer or true superficial fascia and a Muscular tissue, layer of loose connective tissue with perimysium, endomys. the retinaculum cutis profundus. Beneath the hypodermis are the deep and epimysial fasciae. Fig. 1.2. Microscopic image of th e fasciae of the thigh (25x, Haematoxilin-Eosin stain). The Federative Committee on Anatomical Terminology (FCAT) defines the fascia as either a mem­ brane or another aggregation of connective tissue. In this image, it is evident that the fasciae are more complex than this definition: • superficial fascia (A) • aponeurotic fascia (B) • epimysial fascia (C) • muscular tissue (D). 3 ANATOMY OF THE FASCIA Superficial fascia CHAPTER 1 Fig. 1.3. Superficial fascia, re­ gion of the back, being pulled while attached to a dynanometer. Before breaking, the membranous layer of the superficial fascia in the back exhibits a resistance to stretch of approximately 8 kg in a longitudinal direction and 6 kg in a transversal direction.
    [Show full text]
  • The Surgical Anatomy of the Mammary Gland
    NOWOTWORY Journal of Oncology 2020, volume 70, number 5, 211–219 DOI: 10.5603/NJO.2020.0042 © Polskie Towarzystwo Onkologiczne ISSN 0029–540X Varia www.nowotwory.edu.pl The surgical anatomy of the mammary gland (part 1.) General structure, embryogenesis, histology, the nipple-areolar complex, the fascia of the glandular tissue and the chest wall Sławomir Cieśla1, Mateusz Wichtowski1, 2, Róża Poźniak-Balicka3, 4, Dawid Murawa1, 2 1Department of General and Oncological Surgery, K. Marcinkowski University Hospital, Zielona Góra, Poland 2Department of Surgery and Oncology, Collegium Medicum, University of Zielona Góra, Poland 3Department of Radiotherapy, K. Marcinkowski University Hospital, Zielona Góra, Poland 4Department of Urology and Oncological Urology, Collegium Medicum, University of Zielona Góra, Poland The rapid development of surgical techniques used in breast surgery requires an excellent knowledge of mammary gland anatomy. This article presents the most up-to-date information on embryogenesis as well as the histology and general anatomy of the breast. Particular attention has been given to the structure of the nipple-areolar complex and the anatomy of the chest wall and mammary gland fascia. Key words: mammary gland, anatomy, embryogenesis The breasts are paired glands located on the front wall of the Female breasts are subject to continuous changes de- chest within the outer integument. They can be found both in pendent on a number of endogenous factors (primarily females and in males, although they are an anatomical attribute hormones), general health condition or disease, as well of women in a cultural, mental and, above all, functional sense. as exogenous factors related to the nature of physical ac- Anatomical descriptions of female breasts refer to some kind of tivity, work, care, reproduction or breast feeding.
    [Show full text]
  • The Structure and Calcification of the Crustacean Cuticle1
    Amer. Zool., 24:893-909 (1984) The Structure and Calcification of the Crustacean Cuticle1 Robert Roer and Richard Dillaman Institute of Marine Biomedical Research, Universityof North Carolina at Wilmington, Wilmington,North Carolina 28403 Synopsis. The integument of decapod crustaceans consists of an outer epicuticle, an exocuticle, an endocuticle and an inner membranous layer underlain by the hypodermis. The outer three layers of the cuticle are calcified. The mineral is in the form of calcite crystals and amorphous calcium carbonate. In the epicuticle, mineral is in the form of spherulitic calcite islands surrounded by the lipid-protein matrix. In the exo- and endo- cuticles the calcite crystal aggregates are interspersed with chitin-protein fibers which are organized in lamellae. In some species, the organization of the mineral mirrors that of the organic fibers, but such is not the case in certain cuticular regions in the xanthid crabs. Thus, control of crystal organization is a complex phenomenon unrelated to the gross morphology of the matrix. Since the cuticle is periodically molted to allow for growth, this necessitates a bidirec- tional movement of calcium into the cuticle during postmolt and out during premolt resorption of the cuticle. In two species of crabs studied to date, these movements are accomplished by active transport effected by a Ca-ATPase and Na/Ca exchange mech? anism. The epi- and exocuticular layers of the new cuticle are elaborated during premolt but do not calcify until the old cuticle is shed. This phenomenon also occurs in vitro in cuticle devoid of living tissue and implies an alteration of the nucleating sites of the cuticle in the course of the molt.
    [Show full text]
  • Interdural Cavernous Sinus Dermoid Cyst in a Child: Case Report
    CASE REPORT J Neurosurg Pediatr 19:354–360, 2017 Interdural cavernous sinus dermoid cyst in a child: case report Flavio Giordano, MD,1 Giacomo Peri, MD,1 Giacomo M. Bacci, MD, PhD,2 Massimo Basile, MD,3 Azzurra Guerra, MD,4 Patrizia Bergonzini, MD,4 Anna Maria Buccoliero, MD,5 Barbara Spacca, MD,1 Lorenzo Iughetti, MD, PhD,4 PierArturo Donati, MD,1 and Lorenzo Genitori, MD1 1Department of Neurosurgery, 2Neuro-ophthalmology Unit, 3Radiology Unit, and 5Pathology Unit, Anna Meyer Hospital, Firenze; and 4Department of Pediatrics, Ospedale Policlinico, University of Modena, Italy Interdural dermoid cysts (DCs) of the cavernous sinus (CS), located between the outer (dural) and inner layer (membra- nous) of the CS lateral wall, are rare lesions in children. The authors report on a 5-year-old boy with third cranial nerve palsy and exophthalmos who underwent gross-total removal of an interdural DC of the right CS via a frontotemporal approach. The patient had a good outcome and no recurrence at the 12-month follow-up. To the best of the authors’ knowledge this is the second pediatric case of interdural DC described in the literature. https://thejns.org/doi/abs/10.3171/2016.9.PEDS1650 KEY WORDS dermoid cyst; interdural cavernous sinus tumors; ophthalmoplegia; skull base surgery; pterional approach; oncology ERMOID cysts (DCS) are extremely rare benign non- tumors of the CS lateral wall into 3 types: invasive from neoplastic tumors accounting for approximately adjacent structures, interdural, and intracavernous. Inter- 0.04%–0.06% of all intracranial lesions.2,15,16, 22–24 dural tumors are located inside the lateral wall of the CS DThese cysts originate from ectopic inclusions of epithelial between the outer dural layer and the inner membranous cells during closure of the neural tube,3,5,8,27 and are made layer.
    [Show full text]
  • Ferrier J (ST5 Radiology), Kingston K (Consultant Radiologist) Poster 6 York Teaching Hospitals Trust, Wiggington Road, York YO31 8HE MSK
    The role of Ultrasound in the differential diagnosis of palpable abdominal wall lesions Ferrier J (ST5 radiology), Kingston K (Consultant Radiologist) Poster 6 York teaching hospitals trust, Wiggington Road, York YO31 8HE MSK Introduction - Abdominal wall masses can develop insidiously or acutely and as such present to primary care or a variety of secondary care specialities. Ultrasound is often the first line investigation and in many cases the only imaging modality undertaken. Ultrasound is an important tool in assessing abdominal wall lesions. High frequency linear transducers allow detailed assessment of anatomy and high quality imaging of superficial pathology. The exact location of lesions with respect to the layers of the abdominal wall can be determined. Below we describe the anatomy of the anterior abdominal wall and present the differential diagnosis pictorially with 12 illustrative cases. The masses are considered in respect to the layer of the abdominal wall from which they originate. Figure 1a Anatomy - Figure 1a depicts a panoramic ultrasound of the appearance of the anterior abdominal wall with the layers highlighted in figure 1b. The layers of the abdominal wall are well-demonstrated by extended field of view using a high frequency linear transducer and the image is comparable to the classic ‘textbook’ drawing (figure 1c). The most superficial layer of the abdominal wall is the dermis with the subdermis deep to this. Dermis & Subdermis Figure 1b A variable amount of subcutaneous fat lies deep to the dermal layers, this layer includes Camper’s fascia. Fascia/muscle Scarpa’s fascia is a membranous layer which can be seen sonographically overlying the abdominal wall Fat muscles.
    [Show full text]