DOCSLIB.ORG

Feasibility of Constructing Large Underground Cavities: Volume II

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Feasibility of Constructing Large Underground Cavities: Volume II FEASIBILITY OF CONSTRUCTING LARGE UNDERGROUND CAVITIES THE STABILITY OF DEEP LARGE-SPAN UNDERGROUND OPENINGS TECHNICAL REPORT NO. 3-648 Volume II June 1964 Sponsored by Advanced Research Projects Agency ARPA Order No. 260-62 Amendment No. I U. S. Army Engineer Waterways Experiment Station CORPS OF ENGINEERS Vicksburg, Mississippi FEASIBILITY OF CONSTRUCTING LARGE UNDERGROUND CAVITIES THE STABILITY OF DEEP LARGE-SPAN UNDERGROUND OPENINGS TECHNICAL REPORT NO. 3-648 Volume II June 1964 Sponsored by Advanced Research Projects Agency ARPA Order No. 260-62 Amendment No. I U. S. Army Engineer Waterways Experiment Station CORPS OFENGINEERS Vicksburg, Mississippi ARMY-MRC VICKSBURG, MISS." COLORADO SCHOOL OF MINES RESEARCH FOUNDATION, INC. Golden, Colorado THE STABILITY OF DEEP LARGE SPAN UNDERGROUND OPENINGS Prepared for U. S. Army Engineer Waterways Experiment Station Corps of Engineers Vicksburg, Mississippi Contract No. DA-22-079-eng-334 Approved: CoaU 0,. Free! JaVid Cardard, Jr. / Director of Research Mathematician William H. Jurney Project Mathematician Thomas I. Sharps Geologist Project No. 320327 COLORADO SCHOOL OF MINES RESEARCH FOUNDATION TABLE OF CONTENTS Page Part I. Theoretical Considerations 1 The Spherical Cavity 1 The Elastic Case ...... 1 Introduction . 1 Derivation of Solutions for a Spherical Cavity in Uniform Stress Fields 2 Stresses and Displacements Due to Force Operative at a Point 3 Potential Stresses ...... 9 Field Stresses 11 Notes on Derivation of Solutions B and C . 14 The Plastic Case 20 The Prolate Spheroidal Cavity. ... .38 The Elastic Case 38 Introduction 38 Statement of the Problem 38 Three-Function Approach in Elasticity. ... 39 The Oblate Spheroidal Cavity . 51 The Elastic Case 51 Introduction ^ 51 Openings in Layered Media . 59 The Multilayered Case ....... 69 Discussion of Theoretical Results and Optimum Cases .... 77 Spherical Cavity . 77 Prolate Spheroidal Cavity. .... 79 Oblate Spheroidal Cavity ... 81 Conclusions and Optimum Shapes ....... 82 Stresses in Vicinity of Cavity 82 References . 83 COLORADO SCHOOL OF MINES RESEARCH FOUNDATION Table of Contents (continued) Page Part II. Practical Considerations Relating to Cavity Stability 85 The Lithology 85 Local Structure 85 Regional Geology 88 Construction Consideration to Promote Stability. 90 Possible Linings and Support 90 Rock Bursts 91 References 94 Part III. Exploration Program for Selected Sites .... 95 Introduction 95 General Geological Reconnaissance. 96 Detailed Surface Mapping in Area 97 Seismic Surveys 99 Drilling for Exploration 100 Well Logging 102 Initial Stress Measurements 110 Core Logging and Laboratory Tests 114 Estimated Cost and the Time for Exploration Program, Site 3 116 Reference 120 Appendix A, Tables 1 — 53 121 Table 54, Directional Surveying 104 55, Drill Stem Testing 105 56, Dipmeter. 107 57, Sonic Logging 108 58, Summary of Estimated Exploration Costs, Site 3. 119 Figure 1, Rectangular and Spherical Coordinate Systems. 10 2, Reference System for Prolate or Oblate Spheroid , 40 3, 65 4, 71 5, Tentative Schedule Exploration Program, Site 3. 117 Map 1, Proposed Drilling Site 3, Inyo County, California 2, Preliminary Structural Geology Site 3 Area, Argus Peak, Inyo County, California COLORADO SCHOOL OF MINES RESEARCH FOUNDATION ii \ Nomenclature Elastic Cases fx, (/> z) Rectangular coordinates (see Figure 1) Cx, y , z') Rectangular coordinates (see Figure 1) Spherical coordinates (see Figure 1) D'j j, O Unit vector triad for rectangular coordinate system [ct^o , U. p , u Unit vector triad for spherical coordinate system [</, V, w] Displacements in rectangular coordinates , Uj\ Displacements in spherical coordinates ect: Stresses in rectangular coordinates 3 , *c±._ ) ec^ Stresses in spherical coordinates faacfy,"?] "teurvilinlinear components of displacement and stress, respectively </>>&, Harmonic stress functions (displacement potentials) K A , 9) Orthongonal curvilinear coordinates in general, and spheroidal coordinate in particular // ; hz } /}$ Local scale coefficients (j Cosh ac> f»5/'/iA ^Auxiliary position parameters for spheroidal p «Cos j coordinate system ?) 9a > Qo Values of <} , ^ ,/r , Q at <x * a( a* c Cosh cc0 1 Polar and equatorial semiaxes, respectively, r of prolate spheroidal cavity (interchanged for b ' c 57/7/? oz0 J oblate cavity) a b Shape ratio COLORADO SCHOOL OF MINES RESEARCH FOUNDATION C Size constant for spheroidal cavities £*,?,£ Shear modulus, Poisson's ratio and Young's modulus Note: < „*/r dV. $*/* 2V. ^7 r ^-srr^ "5~x^^rrLaplaciana operator 3a y c* ^7 F • Grad Fm 7* J-4^ dx ^ <>y j&zi&e Uniform stress field constants in x, y, and z directions, respectively X/ Ratio of uniform horizontal stress field to s vertical stress field, i.e., crf * cr^ /Jcs * Plastic and Multilayered Cases ¥ Dissipative function 5 Incremental functional 3 Represents partial differential f Integral sign Uj, u/ Tensor components SI Angular velocity vector X; y Xk Denote coordinates juu Elastic constant 5 Second viscosity coefficient &/k > rfk Denote components of two stress tensors (fi A contour integral sign S Denotes small increment ^ Expression denoting analytic functions and 0 S constant X P Denotes analytic function It A constant 6/j Denotes components of strain tensor COLORADO SCHOOL OF MINES RESEARCH FOUNDATION iv (o Density q Acceleration of the gravity field u Displacement vector ux. ~l Components of displacement vector Ur * j'/j Components of stress tensor £ Modulus of elasticity (Young's modulus) V Poisson's ratio f Friction force Critical friction force expressed as a stress Critical friction force to maintain sliding motion G, Shear modulus r Position vector 6(k The Kronecker delta Ujh Time derivatives of strain components or, j- Friction factors C;jki General elastic constants (matrix) y Velocity vector p Pressure Viscosity for incompressible fluid 77^. Momentum flux density tensor cr'k Viscosity stress tensor COLORADO SCHOOL OF MINES RESEARCH FOUNDATION PART I. THEORETICAL CONSIDERATIONS THE SPHERICAL CAVITY The Elastic Case Introduction This portion of the report is concerned with theoretical stress distributions on spherical cavities in homogeneous, isotropic, elastic media. The medium in this solution is con­ sidered to be infinite but the results are applicable to a semi- infinite body, i.e., one having a free surface, provided the cavity is sufficiently far below the free surface. In the discussion of the results it will be shown that the depth to the top of the sphere may be as small as a diameter of the sphere. The basic solutions developed are for cavities in uniform stress fields in the coordinate axial directions. The stress fields being the stresses existing in the medium in the absence of the cavity. The stresses depend on only one of the elastic constants (Poisson's ratio v ). Basic solutions for uniform stress fields are given in Tables 1 — 25, at the surface of the sphere for v = 0.1, 0.2, 0.3 and 0.5. From these tables any desired type of solution (using the proper V ) for a spherical cavity in a uniform type stress field can be computed. These solutions were obtained using the same classic methods as Southwell (Reference 1) and Goodier (Reference 2). They are presented here in a more complete form than in the references cited. Stress concentration factors mentioned herein are of the form where <^3 is the vertical component or the uniform 1 COLORADO SCHOOL OF MINES RESEARCH FOUNDATION 1 stress field in which the cavity is located. A sample derivation follows. Derivation of Solutions for a Spherical Cavity in Uniform Stress Fields The method of obtaining the solution for a spherical cavity in a uniform stress field, is so well-known that only a brief outline of procedure is given in this report. First the "simple" solutions (so called by Boussinesq) of Lord Kelvin (Reference 3, Chap. VIII) connected with forces in the interior of an indefinitely extended elastic body are presented (i.e., those needed). Next potential type solutions are given. These consist of using a harmonic function to generate displacements and stresses which satisfy the equations of equilibrium and compatability for an elastic medium. The procedure is to choose a harmonic function F(x, y, z)( = 0) and assume displacements (u, v, w) = ^Vjr grad F where G = 1 2(1+v ) The stresses and displacements for the uniform stress field under consideration are, of course, needed. Having these a combination of stresses (from those mentioned! is obtained so as to nullify the normal and tangential stresses at any point of the cavity. The method described above has been considered as a special case of the three function procedure in elasticity by Neuber (Reference 7). COLORADO SCHOOL OF MINES RESEARCH FOUNDATION Stresses and Displacements Due to Force Operative at a Point (a) Double compressive force in x direction at (0, 0, K): _.A(/*v) [?4v-/)_X_ -3 x31 " ~£— L ** ^5-J y •3 x*y (7) ; & /2 s" 2 w s~Mi±vl z -3X sZ E &3 f> Where A is an arbitrary constant or in spherical coordinates. U » AJ2ULL 3/*j Cos 9 "3 Cas3 &\ £/** L J v= /4 0+ v) T5/M 4> S/aj 9-3 S/u3 $ S/a/ & Cos 9~\ £p2 L J (Z) z w - AO* v) f Cos $ "3 5//j Cos <p Cos** & ~| - L J °r rzio/vmj [u.VjwJ in dirzci/ons J Up - ^ S/*/z ? Co&2e*5/vZ<t>SnJa& + Cosz4>j ^ lAj .ALLtJlL- \^(4v2) 5/m Cos 4> Cos2 & J ^ Ue » A(i + v) j~C2-4js) S/a/ s/m B Cos <^J COLORADO SCHOOL OF MINES RESEARCH FOUNDATION From (3) z 2 <= T3UP. Aa+V) [-8CV-0 Siu* P Coz*&-2 S/Ki <tj/A/Z0-2Cos d\ * Sfi Ef>3 L ^ + Cos3-<t> Cos*8~3S/aj*? Cosz0+A^ X4) 2 z 2 _ AO+V) \(4v-2) S/u 0-3 S/a/ <6 Cos & •*•/1 ~£fil 1 J v e - ePP +e„+eH [« -V + From (3), (4) and stress-strain relations - ~^r ,3/a/3 ?s c©**-,2 r/*soJ J ^ a pv-^; coS ^ 2 Cg _ jr/-jzv; * 3(zv./) s,aj*<p Cos $ +(4v-z) s>*/**j )<5) ^ ^TcjjjS 0>s**J pr^ s ^ f/+v) S//J ^ S/a/ 9 Cos <j^.
Load more

Recommended publications
  • Poster Final
    Evidence for polyphase deformation in the mylonitic zones bounding the Chester and Athens Domes, in southeastern Vermont, from 40Ar/39Ar geochronology Schnalzer, K., Webb, L., McCarthy, K., University of Vermont Department of Geology, Burlington Vermont, USA CLM 40 39 Sample Mineral Assemblage Metamorphic Facies Abstract Microstructure and Ar/ Ar Geochronology 18CD08A Quartz, Muscovite, Biotite, Feldspar, Epidote Upper Greenschist to Lower Amphibolite The Chester and Athens Domes are a composite mantled gneiss QC Twelve samples were collected during the fall of 2018 from the shear zones bounding the Chester and Athens Domes for 18CD08B Quartz, Biotite, Feldspar, Amphibole Amphibolite Facies 18CD08C Quartz, Muscovite, Biotite, Feldspar, Epidote Upper Greenschist to Lower Amphibolite dome in southeast Vermont. While debate persists regarding Me 40 39 microstructural analysis and Ar/ Ar age dating. These samples were divided between two transects, one in the northeastern 18CD08D Quartz, Muscovite, Biotite, Feldspar, Garnet Upper Greenschist to Lower Amphibolite the mechanisms of dome formation, most workers consider the VT NH section of the Chester dome and the second in the southern section of the Athens dome. These samples were analyzed by X-ray 18CD08E Quartz, Muscovite Greenschist Facies domes to have formed during the Acadian Orogeny. This study diraction in the fall of 2018. Oriented, orthogonal thin sections were also prepared for each of the twelve samples. The thin sec- 18CD09A Quartz, Amphibole Amphib olite Facies 40 CVGT integrates the results of Ar/Ar step-heating of single mineral NY tions named with an “X” were cut parallel to the stretching lineation (X) and normal to the foliation (Z) whereas the thin sections 18CD09B Quartz, Biotite, Feldspar, Amphibole, Muscovite Amphibolite Facies grains, or small multigrain aliquots, with data from microstruc- 18CD09C Quartz, Amphibole, Feldspar Amphibolite Facies named with a “Y” have been cut perpendicular to the ‘X-Z’ thin section.
    [Show full text]
  • Sedimentary Record of Cretaceous And
    SEDIMENT AR Y RECORD OF CRETACEOUS AND TER TIAR Y SALT MOVEMENT, EAST TEXAS BASIN: TIMES, RATES, AND LUMES OF SALT FLOW, IMPLICATIONS TO NUCLEAR-WA TE ISOLATION AND PETROLEUM EXPLO ATION by Steven J. Seni and M. P. A. ackson This work was supported by U.S. Depart ent of Energy and funded under Contract No. DE-AC 7-80ET46617 CONTENTS ABSTRACT . • 00 INTRODUCTION. • 00 Data Base. • 00 Early History of Basin Formation and Infilling • 00 Geometry of Salt Structures • 00 EVOLUTIONARY STAGES OF DOME GROWTH. • 00 Pillow Stage . • 00 Geometry of Overlying Strata . • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraph • 00 Diapir Stage • • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraph • 00 Post-Diapir Stage • 00 Geometry of Surrounding Strata • 00 Depositional Facies and Lithostratigraphy • 00 Holocene Analogues. • 00 Discussion • 00 Significance to Subtle Petroleum Traps • 00 PATTERNS OF SALT MOVEMENT IN TIME AND SPAC • 00 Group 1: Pre-Glen Rose Subgroup (pre-112 Ma) - Periphery of Diapir Province • • 00 Group 2: Glen Rose Subgroup to Washita Group 112 to 98 Ma)-­ Basin Axis • 00 Group 3: Post-Austin Group (86 to 56 Ma) -- Per phery of Diapir Province • • 00 Initiation and Acceleration of Salt Flow • • 00 Overview of Dome History • • 00 RATES OF SALT MOVEMENT AND DOME GROWTH • • 00 Assumptions • • 00 Proven Propositions. • 00 Unproven Propositions • 00 Incorrect Propositions • • 00 Distinguishing Between Syndepositional and Post-D positional Thickness Variations. • 00 The Problem • • 00 Structural Evidence • • 00 Sedimentological Evidence • • 00 Methodology • • 00 Distinguishing Between Regional and Salt-Re ated Thickness Variations. • 00 Volume of Salt Mobilized and Estimates of S t Loss • 00 Rates of Dome Growth • • 00 Net Rates of Pillow Growth • 00 Net Rates of Diapir Growth • 00 Gross Rates of Diapir Growth • • 00 Growth Rates and Strain Rates • 00 IMPLICA TIONS TO WASTE ISOLATION • • 00 CONCLUSIONS • • 00 ACKNOWLEDGMENTS • • 00 REFERENCES • 00 APPENDICES • 00 Figures 1.
    [Show full text]
  • Influences of Surface Processes on Fold Growth During 3D Detachment
    PUBLICATIONS Geochemistry, Geophysics, Geosystems RESEARCH ARTICLE Influences of surface processes on fold growth during 3-D 10.1002/2014GC005450 detachment folding Key Point: M. Collignon1, B. J. P. Kaus2, D. A. May3, and N. Fernandez2 Influences of surface processes on the fold pattern in fold-and-thrust 1Geological Institute, ETH Zurich, Zurich, Switzerland, 2Institut fur€ Geowissenschaften, Johannes Gutenberg-Universit€at, belts Mainz, Germany, 3Institute of Geophysics, ETH Zurich, Zurich, Switzerland Correspondence to: M. Collignon, Abstract In order to understand the interactions between surface processes and multilayer folding sys- [email protected] tems, we here present fully coupled three-dimensional numerical simulations. The mechanical model repre- sents a sedimentary cover with internal weak layers, detached over a much weaker basal layer representing Citation: salt or evaporites. Applying compression in one direction results in a series of three-dimensional buckle folds, Collignon, M., B. J. P. Kaus, D. A. May, and N. Fernandez (2014), Influences of of which the topographic expression consists of anticlines and synclines. This topography is modified through surface processes on fold growth time by mass redistribution, which is achieved by a combination of fluvial and hillslope erosion, as well as during 3-D detachment folding, deposition, and which can in return influence the subsequent deformation. Model results show that surface Geochem. Geophys. Geosyst., 15, doi:10.1002/2014GC005450. processes do not have a significant influence on folding patterns and aspect ratio of the folds. Nevertheless, erosion reduces the amount of shortening required to initiate folding and increases the exhumation rates. Received 9 JUN 2014 Increased sedimentation in the synclines contributes to this effect by amplifying the fold growth rate by grav- Accepted 29 JUL 2014 ity.
    [Show full text]
  • FIELD TRIP: Contractional Linkage Zones and Curved Faults, Garden of the Gods, with Illite Geochronology Exposé
    FIELD TRIP: Contractional linkage zones and curved faults, Garden of the Gods, with illite geochronology exposé Presenters: Christine Siddoway and Elisa Fitz Díaz. With contributions from Steven A.F. Smith, R.E. Holdsworth, and Hannah Karlsson This trip examines the structural geology and fault geochronology of Garden of the Gods, Colorado. An enclave of ‘red rock’ terrain that is noted for the sculptural forms upon steeply dipping sandstones (against the backdrop of Pikes Peak), this site of structural complexity lies at the south end of the Rampart Range fault (RRF) in the southern Colorado Front Range. It features Laramide backthrusts, bedding plane faults, and curved fault linkages within subvertical Mesozoic strata in the footwall of the RRF. Special subjects deserving of attention on this SGTF field trip are deformation band arrays and younger-upon-older, top-to-the-west reverse faults—that well may defy all comprehension! The timing of RRF deformation and formation of the Colorado Front Range have long been understood only in general terms, with reference to biostratigraphic controls within Laramide orogenic sedimentary rocks, that derive from the Laramide Front Range. Using 40Ar/39Ar illite age analysis of shear-generated illite, we are working to determine the precise timing of fault movement in the Garden of the Gods and surrounding region provide evidence for the time of formation of the Front Range monocline, to be compared against stratigraphic-biostratigraphic records from the Denver Basin. The field trip will complement an illite geochronology workshop being presented by Elisa Fitz Díaz on 19 June. If time allows, and there is participant interest, we will make a final stop to examine fault-bounded, massive sandstone- and granite-hosted clastic dikes that are associated with the Ute Pass fault.
    [Show full text]
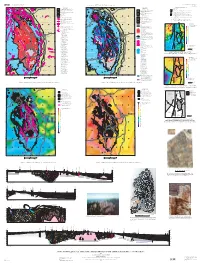
  • Map Showing Geology, Structure, and Geophysics of the Central Black
    U.S. DEPARTMENT OF THE INTERIOR Prepared in cooperation with the SCIENTIFIC INVESTIGATIONS MAP 2777 U.S. GEOLOGICAL SURVEY SOUTH DAKOTA SCHOOL OF MINES AND TECHNOLOGY FOUNDATION SHEET 2 OF 2 Pamphlet accompanies map 104°00' 103°30' 103°00' 104°00' 103°30' 103°00' ° ° EXPLANATION FOR MAPS F TO H 44 30' 44°30' EXPLANATION 44 30' 44°30' EXPLANATION Spearfish Geologic features 53 54 Tertiary igneous rocks (Tertiary and post-Tertiary Spearfish PHANEROZOIC ROCKS 90 1 90 sedimentary rocks not shown) Pringle fault 59 Tertiary igneous rocks (Tertiary and post-Tertiary Pre-Tertiary and Cretaceous (post-Inyan Kara sedimentary rocks not shown) Monocline—BHM, Black Hills monocline; FPM, Fanny Peak monocline 52 85 Group) rocks 85 Sturgis Sturgis Pre-Tertiary and Cretaceous (post-Inyan Kara A Proposed western limit of Early Proterozoic rocks in subsurface 55 Lower Cretaceous (Inyan Kara Group), Jurassic, Group) rocks 57 58 60 14 and Triassic rocks 14 Lower Cretaceous (Inyan Kara Group), Jurassic, B Northern extension (fault?) of Fanny Peak monocline and Triassic rocks Paleozoic rocks C Possible eastern limit of Early Proterozoic rocks in subsurface 50 Paleozoic rocks Precambrian rocks S Possible suture in subsurface separating different tectonic terranes 89 51 89 2 PRECAMBRIAN ROCKS of Sims (1995) 49 Contact St 3 G Harney Peak Granite (unit Xh) Geographic features—BL, Bear Lodge Mountains; BM, Bear Mountain; Fault—Dashed where approximately located G DT DT, Devils Tower 48 B Early Proterozoic rocks, undivided Anticline—Showing trace of axial surface and 1 St Towns and cities—B, Belle Fourche; C, Custer; E, Edgemont; HS, Hot direction of plunge.
    [Show full text]
  • Characterization of Olivine Fabrics and Mylonite in the Presence of Fluid
    Jung et al. Earth, Planets and Space 2014, 66:46 http://www.earth-planets-space.com/content/66/1/46 FULL PAPER Open Access Characterization of olivine fabrics and mylonite in the presence of fluid and implications for seismic anisotropy and shear localization Sejin Jung1, Haemyeong Jung1* and Håkon Austrheim2 Abstract The Lindås Nappe, Bergen Arc, is located in western Norway and displays two high-grade metamorphic structures. A Precambrian granulite facies foliation is transected by Caledonian fluid-induced eclogite-facies shear zones and pseudotachylytes. To understand how a superimposed tectonic event may influence olivine fabric and change seismic anisotropy, two lenses of spinel lherzolite were studied by scanning electron microscope (SEM) and electron back-scattered diffraction (EBSD) techniques. The granulite foliation of the surrounding anorthosite complex is displayed in ultramafic lenses as a modal variation in olivine, pyroxenes, and spinel, and the Caledonian eclogite-facies structure in the surrounding anorthosite gabbro is represented by thin (<1 cm) garnet-bearing ultramylonite zones. The olivine fabrics in the spinel bearing assemblage were E-type and B-type and a combination of A- and B-type lattice preferred orientations (LPOs). There was a change in olivine fabric from a combination of A- and B-type LPOs in the spinel bearing assemblage to B- and E-type LPOs in the garnet lherzolite mylonite zones. Fourier transform infrared (FTIR) spectroscopy analyses reveal that the water content of olivine in mylonite is much higher (approximately 600 ppm H/Si) than that in spinel lherzolite (approximately 350 ppm H/Si), indicating that water caused the difference in olivine fabric.
    [Show full text]
  • Oregon Geologic Digital Compilation Rules for Lithology Merge Information Entry
    State of Oregon Department of Geology and Mineral Industries Vicki S. McConnell, State Geologist OREGON GEOLOGIC DIGITAL COMPILATION RULES FOR LITHOLOGY MERGE INFORMATION ENTRY G E O L O G Y F A N O D T N M I E N M E T R R A A L P I E N D D U N S O T G R E I R E S O 1937 2006 Revisions: Feburary 2, 2005 January 1, 2006 NOTICE The Oregon Department of Geology and Mineral Industries is publishing this paper because the infor- mation furthers the mission of the Department. To facilitate timely distribution of the information, this report is published as received from the authors and has not been edited to our usual standards. Oregon Department of Geology and Mineral Industries Oregon Geologic Digital Compilation Published in conformance with ORS 516.030 For copies of this publication or other information about Oregon’s geology and natural resources, contact: Nature of the Northwest Information Center 800 NE Oregon Street #5 Portland, Oregon 97232 (971) 673-1555 http://www.naturenw.org Oregon Department of Geology and Mineral Industries - Oregon Geologic Digital Compilation i RULES FOR LITHOLOGY MERGE INFORMATION ENTRY The lithology merge unit contains 5 parts, separated by periods: Major characteristic.Lithology.Layering.Crystals/Grains.Engineering Lithology Merge Unit label (Lith_Mrg_U field in GIS polygon file): major_characteristic.LITHOLOGY.Layering.Crystals/Grains.Engineering major characteristic - lower case, places the unit into a general category .LITHOLOGY - in upper case, generally the compositional/common chemical lithologic name(s)
    [Show full text]
  • PLANE DIP and STRIKE, LINEATION PLUNGE and TREND, STRUCTURAL MEASURMENT CONVENTIONS, the BRUNTON COMPASS, FIELD BOOK, and NJGS FMS
    PLANE DIP and STRIKE, LINEATION PLUNGE and TREND, STRUCTURAL MEASURMENT CONVENTIONS, THE BRUNTON COMPASS, FIELD BOOK, and NJGS FMS The word azimuth stems from an Arabic word meaning "direction“, and means an angular measurement in a spherical coordinate system. In structural geology, we primarily deal with land navigation and directional readings on two-dimensional maps of the Earth surface, and azimuth commonly refers to incremental measures in a circular (0- 360 °) and horizontal reference frame relative to land surface. Sources: Lisle, R. J., 2004, Geological Structures and Maps, A Practical Guide, Third edition http://www.geo.utexas.edu/courses/420k/PDF_files/Brunton_Compass_09.pdf http://en.wikipedia.org/wiki/Azimuth http://en.wikipedia.org/wiki/Brunton_compass FLASH DRIVE/Rider/PDFs/Holcombe_conv_and_meas.pdf http://www.state.nj.us/dep/njgs/geodata/fmsdoc/fmsuser.htm Brunton Pocket Transit Rider Structural Geology 310 2012 GCHERMAN 1 PlanePlane DipDip andand LinearLinear PlungePlunge horizontal dddooo Dip = dddooo Bedding and other geological layers and planes that are not horizontal are said to dip. The dip is the slope of a geological surface. There are two aspects to the dip of a plane: (a) the direction of dip , which is the compass direction towards which the plane slopes; and (b) the angle of dip , which is the angle that the plane makes with a horizontal plane (Fig. 2.3). The direction of dip can be visualized as the direction in which water would flow if poured onto the plane. The angle of dip is an angle between 0 ° (for horizontal planes) and 90 ° (for vertical planes). To record the dip of a plane all that is needed are two numbers; the angle of dip followed by the direction (or azimuth) of dip, e.g.
    [Show full text]
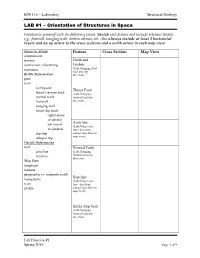
  • EPS 116 – Laboratory Structural Geology Lab Exercise #1 Spring 2016
    EPS 116 – Laboratory Structural Geology LAB #1 – Orientation of Structures in Space Familiarize yourself with the following terms. Sketch each feature and include relevant details, e.g., footwall, hanging wall, motion arrows, etc. Also always include at least 3 horizontal layers and an up arrow in the cross sections and a north arrow in each map view. Stress vs. Strain Feature Cross Section Map View compression tension Horst and contraction/shortening Graben extension (Label hanging /foot wall and slip Brittle Deformation direction) joint fault earthquake Thrust Fault thrust/reverse fault (Label hanging / normal fault footwall and slip footwall direction) hanging wall strike-slip fault right lateral or dextral Anticline left lateral (Label hinge axis, or sinistral force direction, dip-slip contact topo lines in map view) oblique-slip Ductile Deformation fold Normal Fault anticline (Label hanging / footwall and slip syncline direction) Map View longitude latitude geographic vs. magnetic north Syncline topography (Label hinge axis, scale force direction, profile contact topo lines in map view) Strike-Slip fault (Label hanging / footwall and slip direction) Lab Exercise #1 Spring 2016 Page 1 of 9 EPS 116 – Laboratory Structural Geology Strike & Dip Strike and dip describe the orientation of a plane in space. Example: the peaked roof of a house: Strike Line Dip Direction Strike is the orientation of the intersection line of the plane in question (roof of a house) with the horizontal plane. If you were to look down on the house from directly above, it would look like this: North Strike Line Strike The angle between the strike line and north is used to describe the strike.
    [Show full text]
  • TIES, MONTANA. by CF BOWEN. Previo
    ANTICLINES IN A PART OF THE MUSSELSHELL VALLEY, MUSSELSHELL, MEAGHER, AND SWEETGRASS COUN­ TIES, MONTANA. By C. F. BOWEN. INTRODUCTION. Previous investigations had shown that the Musselshell Valley, Mont, is an area in which the rocks have undergone considerable folding. On the basis of this information work was begun in June, 1916, to determine the nature and extent of the folds and to make examination as to the possible occurrence of accumulations of oil and gas in them. The work has demonstrated the existence within the area studied of several well-developed anticlines and domes, which seem to offer structurally favorable places for the accumulation of oil and gas. The demonstration of the presence or absence of commercial accumulations of these fluids in the folds has been less conclusive, owing largely to the undeveloped condition of the area. No direct surface indications of oil were observed, but hydrogen sulphide gas escapes from several water seeps in one part of the area. It is also reported that gas was encountered in several wells dug for water. None of these reports could be verified. At the time of the examination drilling operations within the area were confined to two wells. One of these wells, on the Big Elk dome, had reached the Kootenai formation; the other, in the Woman's Pocket anticline, was probably somewhat more than halfway through the Colorado shale. In neither place had oil been discovered. Two other wells, one about 15 miles east of the area and the other about 12 miles south of the central portion of it, had previously been drilled through the Colo­ rado shale without any discovery of oil.
    [Show full text]
  • The Relationship Between Tectonic Stylolites and Fold Morphology in Limestones of the “Croatica Deposits” (Croatia)
    Geologia Croatica 55/1 79 - 81 4 Figs. ZAGREB 2002 The Relationship Between Tectonic Stylolites and Fold Morphology in Limestones of the “Croatica Deposits” (Croatia) Domagoj JAMIÈIÆ Key words: Stylolites, Tectonics, Compression, lolites appears in the plane perpendicular to the main Limestone, Croatica Deposits, Lower Pannonian, stress (s 1) whereas the second generation is connected Croatia. to extension of left transcurrent fault. This paper describes the tectonic deformational sequence which led to formational processes of tectonic stylolites in Pannonian clayey limestones (“Croatica Abstract Deposits”). The genetic link between faults and fracture Stylolites associated with axial plane fractures occur in Lower Pan- creation and the process of stylolitization under the nonian clayey limestones (the “Croatica Deposits”) from the “Ham- povica 6” deep exploration well. A genetic link has been observed influence of local stress with the same orientation has between the origin of fractures and the process of stylolitization. been noticed. Strong tectonic deformations are present which have been formed Stylolites often occur in limestones and marls, either under the influence of reverse bed faulting. Deformation is pro- nounced in the shape of folded marl layers along with the creation of a) parallel to, or b) at an angle relative to the bedding thick cleavage (0.3-0.5 cm). Along the fractures of axial plane cleav- plane. The first stylolite type, parallel to beds has been age, microlithons are separated and moved apart for similar values (2- formed as a result of gravity and sediment compaction. 5 mm) forming a moderate synform. Stylolites are formed in the last The initial thickness of sediments can be reduced by phase of structure shaping when the effects of the local compressional stress have weakened under the influence of which the breaking off gravitational processes up to 20-30% (TI©LJAR, 1978).
    [Show full text]
  • The Green Mountain Anticlinorium in the Vicinity of Wilmington and Woodford Vermont
    THE GREEN MOUNTAIN ANTICLINORIUM IN THE VICINITY OF WILMINGTON AND WOODFORD VERMONT By JAMES WILLIAM SKEHAN, S. J. VERMONT GEOLOGICAL SURVEY CHARLES G. DOLL, Stale Geologist Published by VERMONT DEVELOPMENT DEPARTMENT MONTPELIER, VERMONT BULLETIN NO. 17 1961 = 0 0. Looking northwest from centra' \Vhitingham, from a point near C in WHITINCHAM IPlate 1 Looking across Sadawga Pond Dome to Haystack Mountain-Searsburg Ridge in the background; Stratton and Glastenburv Mountains in the far distance. Davidson Cemetery in center foreground on Route 8 serves as point of reference. TABLE OF CONTENTS PAGE ABSTRACT 9 INTRODUCTION . . . . . . . . . . . . . . . . . . . . . 10 Location ........................ 10 Regional Geologic Setting . . . . . . . . . . . . . . . 13 Previous Geologic Work ................. 15 The Problem ...................... 16 Present Investigation ................... 18 Acknowledgments .................... 19 Topography . . . . . . . . . . . . . . . . . . . . . 19 Rock Exposure ..................... 20 Culture and Accessibility ................. 20 STRATIGRAPHY AND LITHOLOGY ............... 23 General Statement . . . . . . . . . . . . . . . . . . 23 Stratigraphic Nomenclature . . . . . . . . . . . . . . 25 Lithologic Nomenclature ................. 26 Pre-Cambrian Rocks . . . . . . . . . . . . . . . . . 27 General Statement . . . . . . . . . . . . . . . . . 27 Mount Holly Complex ................. 28 Stamford
    [Show full text]