DOCSLIB.ORG

Austrian Journal of Technical and Natural Sciences

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Austrian Journal of Technical and Natural Sciences Austrian Journal of Technical and Natural Sciences № 7–8 2016 July–August «East West» Association for Advanced Studies and Higher Education GmbH Vienna 2016 Austrian Journal of Technical and Natural Sciences Scientific journal № 7–8 2016 (July–August) ISSN 2310-5607 Editor-in-chief Hong Han, China, Doctor of Engineering Sciences International editorial board Andronov Vladimir Anatolyevitch, Ukraine, Doctor of Engineering Sciences Bestugin Alexander Roaldovich, Russia, Doctor of Engineering Sciences Frolova Tatiana Vladimirovna, Ukraine, Doctor of Medicine Inoyatova Flora Ilyasovna, Uzbekistan, Doctor of Medicine Kushaliyev Kaisar Zhalitovich, Kazakhstan, Doctor of Veterinary Medicine Mambetullaeva Svetlana Mirzamuratovna, Uzbekistan, Doctor of Biological Sciences Nagiyev Polad Yusif, Azerbaijan, Ph.D. of Agricultural Sciences Nemikin Alexey Andreevich, Russia, Ph.D. of Agricultural Sciences Nenko Nataliya Ivanovna, Russia, Doctor of Agricultural Sciences Skopin Pavel Igorevich, Russia, Doctor of Medicine Suleymanov Suleyman Fayzullaevich, Uzbekistan, Ph.D. of Medicine Zhanadilov Shaizinda, Uzbekistan, Doctor of Medicine Proofreading Kristin Theissen Cover design Andreas Vogel Additional design Stephan Friedman Editorial office European Science Review “East West” Association for Advanced Studies and Higher Education GmbH, Am Gestade 1 1010 Vienna, Austria Email: [email protected] Homepage: www.ew-a.org Austrian Journal of Technical and Natural Sciences is an international, German/English/Russian language, peer-reviewed journal. It is published bimonthly with circulation of 1000 copies. The decisive criterion for accepting a manuscript for publication is scientific quality. All research articles published in this journal have undergone a rigorous peer review. Based on initial screening by the editors, each paper is anonymized and reviewed by at least two anonymous referees. Recommending the articles for publishing, the reviewers confirm that in their opinion the submitted article contains important or new scientific results. East West Association GmbH is not responsible for the stylistic content of the article. The responsibility for the stylistic content lies on an author of an article. Instructions for authors Full instructions for manuscript preparation and submission can be found through the “East West” Association GmbH home page at: http://www.ew-a.org. Material disclaimer The opinions expressed in the conference proceedings do not necessarily reflect those of the «East West» Association for Advanced Studies and Higher Education GmbH, the editor, the editorial board, or the organization to which the authors are affiliated. East West Association GmbH is not responsible for the stylistic content of the article. The responsibility for the stylistic content lies on an author of an article. © «East West» Association for Advanced Studies and Higher Education GmbH All rights reserved; no part of this publication may be reproduced, stored in a retrieval system, or transmitted in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without prior written permission of the Publisher. Typeset in Berling by Ziegler Buchdruckerei, Linz, Austria. Printed by «East West» Association for Advanced Studies and Higher Education GmbH, Vienna, Austria on acid-free paper. The construction of the sums of a geometric progression to a degree Section 1. Mathematics Druzhinin Victor Vladimirovich, Alekseev Vladimir Vasilevich National research University “MEPHI” Sarov physical-technical Institute E mail: [email protected] The construction of the sums of a geometric progression to a degree Abstract: The analytical expressions for the erection of sums of geometric progressions to a degree. The results are used for the summation of series, complex finite sums, solving algebraic equations. Keywords: geometric progression, complex finite and infinite sums. In analytical mathematics there are many examples decrease symmetrically, and cfkn= mk− � and �bekn= mk− . We of finite sums and series, with a relatively simple formula have identified the coefficients of the different letters as the result. These include the binomial theorem, sums they are considered by different formulas. The basic of arithmetic and geometric progressions, sums of factors are calculated using binomial coefficient ()n ≥ 2 Bernoulli — ordered amount of the one power, whole and ()mk+−1 ! k cnkm(),m = =C +−k 1. (4) fractional numbers, arithmetic-geometric progressions ()mk−1 !! and other subjects [1; 2; 3; 4]. In this article we focus For the coefficients bk and ds we have not received on the construction in the natural degree m amounts of General formula, but found them to specific m = 234,,�� . a geometric progression If nm is an odd number, then in the middle of the right Ga(,nm,) = row (3) there is not one greatest factor, and two of the m n m n+1 k 23 n m a −1 same factor. If nt=+21,�mp=+21 that are coefficients = �� ∑aa =+()1 ++aa+…+a �= . (1) k=0 a −1 dd22pt ++tp= pt ++tp+1. Subsequently the coefficients of mirror In reference books and educational literature we have symmetry occurs. not found this problem. Meanwhile here there is a large If m = 2 then n 2 n 2n set of new deemed according to the formula amounts and k k k Ga(),,na21= ∑∑ =+� ()ka++∑ ()21nk− a. (5) ranks as well as taking the integrals and the solution of k==0 k 01kn=+ For example, algebraic equations. In (1) the final result is the right side, 2 but as reveals the amount of degree, what its symmetry ()11++aa2 =+23aa++232aa+ 4 , (6) 2 and structure are we show below. First we write the ()11++aa23+aa=+23++aa2343++aa452 +a 6 . (7) polynomial theorem From identities (6 –7) a symmetry of the right and n m m! tt12 tn left parts and an algorithm for the construction of any ∑∑xk =� ()xx12()...()xn ,, (2) k=0 ()tt12!!()...()t n ! geometric progression is in the square. where ()tt12++…+tmn = and the sum goes through all In the construction of Ga(,n,)3 in the cube we obtain combinations of these numbers. With the special the following result. If n is even, nt= 2 , if xx= k 2 structure of numbers k � (our case) the left part is 21tk+≤ ≤−31tb,;��k =+13tt()+1 −−()mt k nm +1 much easier. Number of terms is (), the highest dt3t =+13()t +1 . Examples a nm nm 23456 degree is . General record in even has a view Ga(),,23 =+13aa++67aa++63aa+ . (8) n s −1 21sn−− mn 234 k k s k k Ga(),,43� =+13aa++6101aa++5 Ga(),,nm =+∑∑cak bak ++das ∑ eak + ∑ fak . (3) k==01kn+ ks=+1 k=2ssn− 56712 (9) k ++18aaa 19++ 18 …+a . Coefficients with increasing monotonically increase 567 d d Ga(),,63� =+12…+12aa83++3a up to including s . The central coefficient s has the (10) greatest value. The following ratios monotonically ++36aa89 37+… 36aa10+ 18 . 3 Section 1. Mathematics 456 If n is odd, nt=+21, then 22tk+≤≤=31tb,;��31tq+− dq 31t + −+()q Ga(),,44� =+13…+ 55aa++268a + (15) 22tk+≤≤=31tb,;dq−+q 11≤≤qt− 78916 ��31tq+− 31t + () . The highest coefficients ++ 80aa 85+… 80aa+ . dd==31t + 2 . 31tt++32 () Examples It is also possible to obtain other degrees Ga(),,nm� . Ga(),,33� =+13aa++6123401aa++2 (11) Consider the possible applications of these structures. ++12aa56 10 ++63aa78+a 9 .� 1. The sum of a convergent series of generalized Ga(),,53 =+13aa++612301aa++5 4 geometric progression with 01<<a species arises (12) 56718 ∞ ++21aa 25++ 27aa…+ .� ()mk+−1 ! k 1 ∑ a = m .� � � (16) These amounts are calculated according to right side k=0 ()mk−1 !! ()1−a (1). In the construction of Ga(,n,)4 in the fourth degree a we get such formulas, regardless of the evenness or 2. If we take the derivative at , we get the new calculated amount. For example, ∂Ga(),,23� / ∂a gives unevenness of n . If kn==21,/�dn2n ++52nn()−14()n + 3 kn==21,/dn++52nn−14n + 3 3 2 2 � 2n ()(), the maximum value of the ()aa−12()−−a 1 ++23++45+= kn=−21� 14aa78aa52a 3 .(17)� coefficient. If have the greatest ()a −1 bd21nn− =−2 ()n +1 . The other coefficients b2nl− , with 12≤≤ln− are calculated by recurrent relations 3. There appears the possibility of analytical solutions 2 bb21nl−− =−2 nl− ()21ln+ +−()32ll− /.2 � of algebraic equations of high order. The equation Examples 65432 23 aa++36aa++76aa+−3260= � is reduced to the Ga(),,24� =+14aa++10 16a + 2 (13) equation aa+−20= � which has two aa12==12,� − . ++45+…+ 8 19aa 16 a .� � 4. Combinations of sums and products of Ga(),,nm� Ga(),,34� =+14aa++1023 20aa++ 31 4 (14) form a new hope of final amount and series and also give ++40aa56 44++ 40aa71.. + 2 . the opportunity to find the integral analytically. References: 1. Sizyi S. V. Lectures on the theory of numbers, FIZMATGIZ, – M., 2007. 2. Korn. G., Korn. T. Handbook of mathematics, Science, GHML, – M., 1974. P. 31, 135. 3. Gradshteyn I. S., Ryzhik I. – M. Tables of integrals, sums, series and products. GIFML, – M, 1962. P. 15–16. 4. Druzhinin V. V., Sirotkina A. G. NTVP, No. 4, 2016, P. 15–16. 4 The construction of the sums of a geometric progression to a degree Section 2. Medical science Anoshina Tatiana Nikolaevna, PhD, Assistant of the Department of Obstetrics, Gynecology and Reproduction, Shupik National Medical Academy of Postgraduate Education, Kyiv, Ukraine E-mail: [email protected] Clinical course of genital herpes in HIV-infected pregnant women Abstract: HIV-infected pregnant women have severe manifestations of the clinical course of genital herpes, which was accompanied by a characteristic colpo- and vulvoscopic picture (inflammatory background, herpes vesicles, ulcers, erosion, hyperemia, apparent edema, serous-inflammatory discharge, multi-vessels, severe reaction on acetic acid, rough epithelial relief with micropapillary needled like outgrowths of the connective tissue). It was demonstrated the expediency of express diagnostics (Tzanck sample, Schiller test). There were specific for HSV cytologic manifestations: increased sizes of nuclei in epithelial cells, form of watch-glass, multinucleated cells, muddy unstructured chromatin.
Load more

Recommended publications
  • USMLE – What's It
    Purpose of this handout Congratulations on making it to Year 2 of medical school! You are that much closer to having your Doctor of Medicine degree. If you want to PRACTICE medicine, however, you have to be licensed, and in order to be licensed you must first pass all four United States Medical Licensing Exams. This book is intended as a starting point in your preparation for getting past the first hurdle, Step 1. It contains study tips, suggestions, resources, and advice. Please remember, however, that no single approach to studying is right for everyone. USMLE – What is it for? In order to become a licensed physician in the United States, individuals must pass a series of examinations conducted by the National Board of Medical Examiners (NBME). These examinations are the United States Medical Licensing Examinations, or USMLE. Currently there are four separate exams which must be passed in order to be eligible for medical licensure: Step 1, usually taken after the completion of the second year of medical school; Step 2 Clinical Knowledge (CK), this is usually taken by December 31st of Year 4 Step 2 Clinical Skills (CS), this is usually be taken by December 31st of Year 4 Step 3, typically taken during the first (intern) year of post graduate training. Requirements other than passing all of the above mentioned steps for licensure in each state are set by each state’s medical licensing board. For example, each state board determines the maximum number of times that a person may take each Step exam and still remain eligible for licensure.
    [Show full text]
  • Cytomegalovirus Infection of the Human Gastrointestinal Tract
    Journal of Gastroenterology and Hepatology (1999) 14, 973–976 OESOPHAGOGASTRODUODENAL DISORDERS Cytomegalovirus infection of the human gastrointestinal tract SUSAMA PATRA, SUBASH C SAMAL, ASHOK CHACKO, VADAKENADAYIL I MATHAN1 AND MINNIE M MATHAN1 The Wellcome Trust Research Laboratory, Department of Gastrointestinal Sciences, Christian Medical College and Hospital,Vellore,India Abstract Background: Current interest in cytomegalovirus (CMV) is largely due to an increase in the number of cases of acquired immunodeficiency syndrome and organ transplantation in recent years.The proper recognition of CMV-infected cells in gastrointestinal mucosal biopsies is critical for effective treatment of this condition. Methods: A total of 6580 endoscopic mucosal biopsies from 6323 patients in the 8-year period (1989–1996) were examined for CMV inclusion bodies. The endoscopic appearance and particularly the presence of ulcers were also analysed. Results and Conclusions: The prevalence of cytomegalovirus (CMV) inclusions was 9 per thousand in the gastrointestinal mucosal biopsies from an unselected group of patients. Of the 54 patients with CMV infection, 37 were immunocompromised and 17 apparently immunocompetent. Typical Cowdry inclusions and atypical inclusions were present, the latter more frequently in immunocompromised patients. The maximum prevalence of inclusions was in the oesophageal mucosa in immunocompro- mised individuals. © 1999 Blackwell Science Asia Pty Ltd Key words: cytomegalovirus, gastrointestinal tract, immunocompetent, immunocompromised, inclu- sion bodies, mucosal biopsies. INTRODUCTION in haematoxylin and eosin (HE)-stained histological samples is regarded as being sensitive and specific for Cytomegalovirus (CMV), first described in 1956,1 is a CMV infection,6–9 especially for samples from the gas- double-stranded DNA virus belonging to the herpes trointestinal tract.
    [Show full text]
  • Cytomegalovirus Infection in Gastrointestinal Tract: a Case Series of Three Patients and Review of Literature
    Published online: 2019-10-01 Case Report Cytomegalovirus infection in gastrointestinal tract: A case series of three patients and review of literature Piyush Ranjan, Varun Gupta, Mohan Goyal, Shashi Dhawan1, Pallav Gupta1, Mandhir Kumar, Munish Sachdeva Departments of Gastroenterology and 1Pathology, Sir Ganga Ram Hospital, New Delhi, India Abstract Cytomegalovirus disease can involve any site of gastrointestinal tract from oral cavity to rectum. CMV disease most frequently occurs in patients’ with immune deficiency, such as the acquired immunodeficiency syndrome, after organ transplantation, after cancer chemotherapy and in patients on immunosuppressive medications. The number of patients with immune deficiency has increased in recent years and has lead to a substantial increase in incidence of opportunistic CMV virus. Gastrointestinal CMV infection has also been reported in immunocompetent adults. Symptoms and signs depend on part of the gastrointestinal tract involved. Diagnosis depends either on a positive mucosal biopsy or by serology, quantitative PCR or CMV antigenemia. We report three cases of CMV infection in patients with three different underlying conditions and discuss the clinical features, diagnostic approach and treatment. All patients had positive serology with high viral load on PCR. Histology with immunohistochemistry was positive for CMV in two of the three cases. Ganciclovir response was seen in all patients in respect to clinical improvement, endoscopic resolution of lesions and clearing of the virus load. Key words
    [Show full text]
  • Cytomegalovirus Disease in Patient with HIV Infection
    ntimicrob A ia f l o A l g a e n n Fane et al., J Antimicro 2016, 2:1 r Journal of t u s o J DOI: 10.4172/2472-1212.1000108 ISSN: 2472-1212 Antimicrobial Agents Review Article Open Access Cytomegalovirus Disease in Patient with HIV Infection EL Fane M1*, Sodqi M1, EL Rherbi A2, Chakib A1, Oulad Lahsen A1, Marih L1 and Marhoum EL Filali K1 1Department of Infectious Diseases, CHU Ibn Rocd, Casablanca, Morocco 2Centre Poison Control and Pharmacovigilance Morocco, Rabat, Morocco Summary the incidence of CMV retinitis [3]. The frequency is described to be low in the sub-Saharan Africa (inferior to 10%). This can be explained by Cytomegalovirus (CMV) disease is a serious condition due to the high rate of early mortality and variable population susceptibility reactivation of previously latent infection or newly acquired infection, to develop a CMV disease [8,9]. In Morocco, Data concerning it occurs frequently in immunocompromised patients by HIV epidemiologic profile of CMV disease are lacking; there is a huge need infection. Even it is actually uncommon in the developed nations with of cohort studies in this field [1]. However, some small retrospective the widespread use of highly active antiretroviral therapy (HAART), studies showed CMV retinitis incidence rates close to 4% that remains CMV disease continues to be among the most common opportunistic too low comparing to other African countries [8, 9]. In south Asia, rates infections in patient living with HIV (PLWH) in developing countries. approaching 20 to 30% are noticed [10]. Its severity is linked to its tropism for retina and central nervous system (CNS).
    [Show full text]
  • F-Jonathan Eisenstat, MD-March 24, 2016
    In The Matter Of: Pressgrove, et al v. Byrd, et al Jonathan Eisenstat, MD March 24, 2016 D'Amico Gershwin, Inc. Court Reporters & Videoconferencing 11475 West Rd, Roswell, GA 30075 (770) 645-6111 or toll-free (888) 355-6111 Min-U-Script® with Word Index IN THE CIRCUIT COURT OF TENNESSEE FOR THE THIRTIETH JUDICIAL DISTRICT AT MEMPHIS, SHELBY COUNTY BEVERLY PRESSGROVE and ) PHILLIP SIMMS, individually ) and as next of kin of ) HOLLAND N. SIMMS, ) ) Plaintiffs, ) No. CT-004425-08 ) Division VII vs. ) ) JURY DEMANDED WILLIAM G. BYRD, MD, et al., ) ) Defendants. ) _____________________________) Videotaped deposition of JONATHAN EISENSTAT, M.D., taken on behalf of the Plaintiffs, pursuant to the stipulations contained herein, reading and signing of the deposition being reserved, in accordance with the Tennessee Rules of Civil Procedure, before Stephanie K. Feen, Certified Court Reporter, at 5855 Sandy Springs Circle, Suite 140, Atlanta, Georgia, on the 24th day of March, 2016, commencing at the hour of 12:08 p.m. D'AMICO GERSHWIN, INC. Court Reporters & Videoconferencing 11475 West Road Roswell, Georgia 30075 (770) 645-6111 www.AtlantaCourtReporter.com D'Amico Gershwin, Inc. www.AtlantaCourtReporter.com 1 I N D E X T O E X A M I N A T I O N S 2 Page 3 Examination by Mr. Smith 11 4 5 I N D E X T O E X A M I N A T I O N S 6 Plaintiffs' Description Marked/First Exhibit Identified 7 P-1 Notice of Video Deposition 15 8 of Jonathan Eisenstat, M.D. 9 P-2 Dr.
    [Show full text]
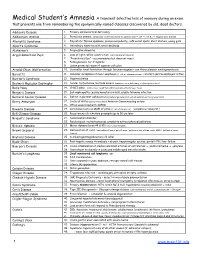
  • 1 Medical Student's Amnesia a Transient Selective Loss of Memory During an Exam That Prevents One from Remem
    Medical Student’s Amnesia A transient selective loss of memory during an exam that prevents one from remembering the eponymically-named diseases discovered by old, dead doctors. Addison’s Disease 1. Primary adrenocortical deficiency Addisonian Anemia 2. Pernicious anemia (antibodies to intrinsic factor or parietal cells → ↓IF → ↓Vit B12 → megaloblastic anemia) Albright’s Syndrome 3. Polyostotic fibrous dysplasia, precocious puberty, café au lait spots, short stature, young girls Alport’s Syndrome 4. Hereditary nephritis with nerve deafness Alzheimer’s 5. Progressive dementia Argyll-Robertson Pupil 6. Loss of light reflex constriction (contralateral or bilateral) 7. “Prostitute’s Eye” – accommodates but does not react 8. Pathognomonic for 3°Syphilis 9. Lesion pretectal region of superior colliculus Arnold-Chiari Malformation 10. Cerebellar tonsil herniation through foramen magnum = see thoracolumbar meningomyelocele Barrett’s 11. Columnar metaplasia of lower esophagus (↑ risk of adenocarcinoma)- constant gastroesophageal reflux Bartter’s Syndrome 12. Hyperreninemia Becker’s Muscular Dystrophy 13. Similar to Duchenne, but less severe (mutation, not a deficiency, in dystrophin protein) Bell’s Palsy 14. CNVII palsy (entire face; recall that UMN lesion only affects lower face) Berger’s Disease 15. IgA nephropathy causing hematuria in kids, usually following infection Bernard-Soulier Disease 16. Defect in platelet adhesion (abnormally large platelets & lack of platelet-surface glycoprotein) Berry Aneurysm 17. Circle of Willis (subarachnoid bleed) Anterior Communicating artery 18. Often associated with ADPKD Bowen’s Disease 19. Carcinoma in situ on shaft of penis (↑ risk of visceral ca) [compare w/ Queyrat] Brill-Zinsser Disease 20. Recurrences of rickettsia prowazaki up to 50 yrs later Briquet’s Syndrome 21.
    [Show full text]
  • Prezentacja Programu Powerpoint
    C5. INFECTIOUS DISEASES LEARNING OBJECTIVES MICROBIAL 1. Compare and contrast various routes of entry of infectious PATHOGENESIS agents (skin, respiratory, gastrointestinal and urogenital tract). Describe mechanisms by which infectious agents evade local defenses. Give examples of microbes that use these routes of entry. 2. Describe routes of dissemination of infectious agents. Give examples of microorganisms that use various modes of dissemination. 3. Describe routes of transmission of infectious agents from person to person. Give examples of pathogens that use various „exit strategies”. 4. Describe routes through which vertical transmission of infectious agents may occur. Give examples of microobes that use these routes of transmission. 5. List mechanisms by which infectious agents damage host tissues. 6. Describe morphologic patterns of tissue responses to infection with regard to pathogenesis and macro- and microscopic features. Give examples of microorganisms that evoke such responses. C4. Inflammation and Repair VIRAL 7. Discuss mechanisms by which viruses cause injury to cells. INFECTIONS 8. Describe acute viral infections (measels and mumps) in terms of pathogenesis, morphologic features and clinical manifestations. Define Koplik spots and Warthin-Finkeldey cells. 9. Describe latent viral infections (HSV, VZV and CMV) with regard to pathogenesis, morphologic features and clinical manifestations. Define intranuclear inclusions, Cowdry bodies, cold sores, chickenpox and shingles. LEARNING OBJECTIVES BACTERIAL 10. Discuss mechanisms by which bacteria cause injury to cells. INFECTIONS Give examples of bacteria that use particular mechanisms. 11. Define endotoxins and exotoxins. List types of exotoxins. 12. Describe staphylococcal infections in terms of pathogenesis, morphologic features and clinical manifestations. Define furuncule (boil), carbuncule, hidradenitis, paronychia, felons and staphylococcal scalded-skin syndrome.
    [Show full text]
  • Laboratory Workbook in Virology
    LABORATORY WORKBOOK IN VIROLOGY Student name ________________________________ Faculty _____________________________________ Group ___________ Minsk BSMU 2016 МИНИСТЕРСТВО ЗДРАВООХРАНЕНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ БЕЛОРУССКИЙ ГОСУДАРСТВЕННЫЙ МЕДИЦИНСКИЙ УНИВЕРСИТЕТ КАФЕДРА МИКРОБИОЛОГИИ, ВИРУСОЛОГИИ, ИММУНОЛОГИИ ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ВИРУСОЛОГИИ LABORATORY WORKBOOK IN VIROLOGY 3-е издание Минск БГМУ 2016 УДК 578.7(811.111)-054.6(076.5) (075.8) ББК 52.63(81.2 Англ-923) Л12 Рекомендовано Научно-методическим советом университета в качестве лабораторного практикума 18.11.2015 г., протокол № 3 А в т о р ы: Д. А. Черношей, В. В. Слизень, Т. А. Канашкова, Т. Г. Адамович Р е ц е н з е н т ы: канд. мед. наук, доц. В. Э. Бутвиловский; канд. мед. наук, доц. А. М. Дронина Лабораторный практикум по вирусологии = Laboratory workbook in virology : лаб. Л12 практикум / Д. А. Черношей [и др.]. – 3-е изд. – Минск : БГМУ, 2016. – 24 с. ISBN 978-985-567-397-3. Содержит информацию для подготовки к практическим занятиям по разделу «Вирусология». Приведены схемы, алгоритмы, справочные сведения, методики выполнения лабораторных работ. Первое издание вышло в 2013 году. Предназначен для студентов 3-го курса медицинского факультета иностранных учащихся (специальность «Лечебное дело»), обучающихся на английском языке. УДК 578.7(811.111)-054.6(076.5) (075.8) ББК 52.63(81.2 Англ-923) ___________________________________________ Учебное издание Черношей Дмитрий Александрович Слизень Вероника Вячеславовна Канашкова Татьяна Александровна Адамович Татьяна Григорьевна ЛАБОРАТОРНЫЙ ПРАКТИКУМ ПО ВИРУСОЛОГИИ LABORATORY WORKBOOK IN VIROLOGY На английском языке 3-е издание Ответственная за выпуск Т. А. Канашкова Переводчик Д. А. Черношей Подписано в печать 19.11.15. Формат 60 84/8. Бумага писчая «Снегурочка». Ризография. Гарнитура «Times».
    [Show full text]
  • PATHOLOGY of HIV/AIDS 32Nd Edition
    PATHOLOGY OF HIV/AIDS 32nd Edition by Edward C. Klatt, MD Professor of Pathology Department of Biomedical Sciences Mercer University School of Medicine Savannah, Georgia, USA July 20, 2021 Copyright © by Edward C. Klatt, MD All rights reserved worldwide 2 DEDICATION To persons living with HIV/AIDS past, present, and future who provide the knowledge, to researchers who utilize the knowledge, to health care workers who apply the knowledge, and to public officials who do their best to promote the health of their citizens with the knowledge of the biology, pathophysiology, treatment, and prevention of HIV/AIDS. 3 TABLE OF CONTENTS 3.................................................................................................................................2 CHAPTER 1 - BIOLOGY AND PATHOGENESIS OF HIV INFECTION.....6 INTRODUCTION......................................................................................................................6 BIOLOGY OF HUMAN IMMUNODEFICIENCY VIRUS................................................10 HUMAN IMMUNODEFICIENCY VIRUS SUBTYPES.....................................................29 OTHER HUMAN RETROVIRUSES....................................................................................31 EPIDEMIOLOGY OF HIV/AIDS.........................................................................................36 RISK GROUPS FOR HUMAN IMMUNODEFICIENCY VIRUS INFECTION.............46 NATURAL HISTORY OF HIV INFECTION......................................................................47 PROGRESSION OF HIV
    [Show full text]
  • Lennette's Laboratory Diagnosis of Viral
    Lennette’s Laboratory Diagnosis of Viral Infections NFECT I OUS I SEASE Fourth Edition Fourth I D Edition AN D THERAPY SER I ES About the book Volume 50 • Written from the perspective of the diagnostician, this bestselling book is the definitive text on the laboratory diagnosis of human viral diseases. • Contains a wealth of illustrations, tables, and algorithms to enhance your understanding of Viral Infections Viral of Lennette’s Lennette’s of this ever-evolving field. • A ready reference source for virologists, microbiologists, epidemiologists, laboratorians, infectious disease specialists and students. Laboratory Unique features • Has a new syndromic approach and discusses the differential diagnosis of potential causative agents along with suggestions for the appropriate diagnostic response. Diagnosis of • Examines the field’s rapid changes in technology, the continuing emergence of new viruses, and the newly described viral etiologies for clinical syndromes. Laboratory Diagnosis • Explores the increasingly important subject of molecular techniques in detail, covering the design of molecular tests, the importance of genotyping and viral Viral Infections sequence analysis, and the use of microarrays in diagnostic virology. Reviews of previous editions Fourth Edition a worthy addition to the bookshelves of the specialised virus laboratory as it contains a wealth of information not readily available elsewhere. The Journal of Clinical Pathology a comprehensive and valuable addition to any medical library. It will appeal to all students of virology, medical microbiology and infectious diseases. The information is set out in a user-friendly fashion and allows the reader to obtain pertinent information without being deluged with too many data [...] recommend[ed] highly.
    [Show full text]
  • An Electrodermal Analysis of Biological Conductance
    An Electrodermal Analysis of Biological Conductance Guidebook for Locating Electrodermal Detection Sites Surface Atlas of Detection Sites Glossary of Computer Codes in Plain Language Protocol for Electrodermal Screening Process of Iteration for Correcting Non-Conductance Conductance in the Complex Human Biological System By Vincent J. Speckhart, M.D., M.D.(H) Published by: Biological Conductance Inc. 1340-1272 N. Great Neck Road Box 188 Virginia Beach, VA 23454 E-mail orders: [email protected] All rights reserved. No part of this book may be reproduced or transmitted in any form or by any means, electronic or mechanical, including photocopying, recording or by any information storage and retrieval system, without written permission from the author, except for the inclusion of brief quotations in a review. Copyright © 2004 First Printing 2004 Printed in the United States of America ISBN 0-9741533-0-3 i ii Acknowledgments I wish to thank Jim Jose, Douglas C. Leber and John Shell for developing the Acupro II System. Most of the data for this study was obtained using this software system. Other good detection devices are available and have been used successfully in obtaining similar data, but the Acupro II System gave me the best range of data that I wanted to include in this study. As a graphic artist, Lee Troxell demonstrated exceptional talent in developing the open and clear graphics for use in the Atlas. He has shown equal skill in converting these images into my computerized program for electrodermal detection. It has been a rocky road in getting a study of this technology to be approved or at least tolerated by those appointed to regulate such activities.
    [Show full text]
  • Pathology.Pre-Test.Pdf
    Pathology PreTestTMSelf-Assessment and Review Notice Medicine is an ever-changing science. As new research and clinical experience broaden our knowledge, changes in treatment and drug therapy are required. The authors and the publisher of this work have checked with sources believed to be reliable in their efforts to provide information that is complete and generally in accord with the standards accepted at the time of publication. However, in view of the possibility of human error or changes in medical sciences, neither the authors nor the publisher nor any other party who has been involved in the preparation or publication of this work warrants that the information contained herein is in every respect accurate or complete, and they disclaim all responsibility for any errors or omissions or for the results obtained from use of the information contained in this work. Readers are encouraged to confirm the information contained herein with other sources. For example, and in particular, readers are advised to check the product information sheet included in the package of each drug they plan to administer to be certain that the information contained in this work is accurate and that changes have not been made in the recommended dose or in the contraindications for administration. This recommendation is of particular importance in connection with new or infrequently used drugs. Pathology PreTestTMSelf-Assessment and Review Twelfth Edition Earl J. Brown, MD Associate Professor Department of Pathology Quillen College of Medicine Johnson City, Tennessee New York Chicago San Francisco Lisbon London Madrid Mexico City Milan New Delhi San Juan Seoul Singapore Sydney Toronto Copyright © 2007 by The McGraw-Hill Companies, Inc.
    [Show full text]