DOCSLIB.ORG

–1– 5. Thermal Properties and Line Diagnostics for HII Regions 5.1

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
–1– 5. Thermal Properties and Line Diagnostics for HII Regions 5.1 { 1 { 5. Thermal Properties and Line Diagnostics for HII Regions 5.1. Heating and Cooling The temperature of the ISM is governed by a number of heating and cooling processes. These include both adiabatic changes in volume, which do not alter the entropy of the gas, and collisional and radiative processes that do. The First Law of Thermodynamics can be expressed as de = dq ¡ pd½¡1; (1) where dq is the heat added to the system per unit mass, ½¡1 the speci¯c volume (i.e., volume per unit mass), 1 p e = + e (2) γ ¡ 1 ½ I the speci¯c energy, γ the ratio of speci¯c heats, and eI the speci¯c chemical binding plus ionization 5 energy. For a monatomic gas, γ = 3 , whereas a gas of diatomic molecules at about room temperture 7 has two additional degrees of freedom and γ = 5 . At temperatures low enough that the rotational 5 degrees of freedom cannot be excited (as is the case for H2 in cold molecular clouds), γ = 3 . Here we shall assume that γ = const, noting that the results here must be modi¯ed if one wishes to treat the case in which molecular gas is heated from low to moderate temperatures. The chemical/ionization ¡1 energy term is eI = ½ n®I®, where ® labels the ion species and I® is the chemical/ionization energy per particle. For convenience, we de¯ne the zero point for e to consist of neutral atoms P I (H I). It follows that IH¤ = 13:6 eV and IH2 = ¡4:48 eV. Let ¹ be the mass per particle so that ½ = n¹, where n is the number density of particles, and p = nkT = ½kT=¹. Converting equation (1) to a rate equation and factoring out p=½ = kT=¹, we ¯nd dq p 1 d p 1 de = ln + d ln + I ; (3) dt ½ γ ¡ 1 dt ½ ½ dt · µ ¶ µ ¶¸ kT d p de = ln + I ; (4) ¹(γ ¡ 1) dt ½γ dt µ ¶ where d=dt = @=@t + v ¢ 5 is the comoving, or Lagrangian, derivative. The quantity ½dq is the total amount of heat added to the gas per unit volume. If dq = 0, the process is said to be adiabatic; for γ deI = 0, this implies p / ½ . Since heating processes are generally per particle, we de¯ne the heating rate per unit volume 1 as nH¡. Cooling processes generally involve collisions between two particles, so they scale as the 1 The mass density ½ can also be written in terms of the number density of hydrogen nuclei as ½ = nH¹H, where ¹H ¡24 is the mass per hydrogen nucleus. For a He abundance that is 10% that of hydrogen, ¹H = 1:4mH = 2:34 £ 10 g. Expressing the mass density in terms of nH is convenient if the gas is being ionized, for example, since then nH is constant at ¯xed volume, whereas n changes. Equivalently, ¹H is a constant in an ionizing gas, but ¹ changes. { 2 { 2 2 square of the density; we therefore write the cooling rate per unit volume as nH¤. The total rate at which heat is added to the gas per unit volume is then dq p d p de ½ = n ¡ ¡ n2 ¤ = ln + ½ I : (5) dt H H γ ¡ 1 dt ½γ dt µ ¶ 5 For γ = 3 and constant composition, this simpli¯es to d 3 dn n kT ¡ kT = n ¡ ¡ n2 ¤; (6) dt 2 dt H H which is the form given in Spitzer (eq. 6.1). If the gas is in a steady state, equation (5) becomes ¡ = nH¤ (steady state). (7) It is sometimes convenient to describe the evolution of the thermal state of the gas in terms of the speci¯c entropy s. For reversible processes, T ds = dq; for irreversible ones (like shocks), T ds ¸ dq, which is a statement of the Second Law of Thermodynamics. The speci¯c entropy is a function of the state variables of the system, s = s[T; n(H0); n(H+); n(He0); :::]. For reversible processes with constant composition and internal energy (¹; eI const), equation (4) can be integrated to give the speci¯c entropy of the gas, k T 1=(γ¡1) s = ln + const. (8) ¹ " n # 5 For γ = 3 the argument of the logarithm is proportional to the volume in phase space, as expected, since T 3=2=n / momentum3 £ volume. 5.1.1. Heating and Cooling Processes Here we shall give a brief summary of the heating and cooling processes that occur throughout the ISM, not just in H II regions. The heating processes fall into several categories: Radiative heating processes, nH¡ = 4¼·J: - Photoionization (Lec. 4). This dominates the heating of H II regions and of the warm ionized medium (WIM) in the ISM. - X-ray photoionization: This requires special treatment for two reasons. First, much of the heating is to due photoionization of the metals, in which the X-ray knocks out a K- shell electron. Second, the electron that is ionized has a high energy and can collisionally ionize and excite other atoms and heat ambient electrons (see Wol¯re et al 1995). 2 Note that some people rede¯ne ¡ and ¤ so as to include the deI =dt term. For example, if a 1 eV electron recombines to the ground state of hydrogen, the energy loss would be taken to be 1 eV instead of 14.6 eV, which is the energy emitted. { 3 { - Photoelectric heating by dust: When FUV photons are absorbed by dust grains, a photoelectron is ejected, heating the ambient gas. This is believed to dominate the heating of the H I in the ISM. - Photodissociation heating: This is analogous to photoionization heating, except that it occurs when H2 molecules are photodissociated. - Collisional heating (or cooling) by dust: As we shall see in the next two lectures, dust is coupled very strongly to optical and UV radiation, so it is possible for the dust to be at a di®erent temperature than the gas. Near strong sources of radiation, such as early-type stars, the dust can be hotter than the gas, and the gas will be heated by collisions with the dust grains. Since this is a collisional process that varies as n2, it is important only at high densities. Dynamical heating - Shock heating: Shocks are hydrodynamic discontinuities in that the equations of hy- drodynamics, which are based on small mean free paths, break down in the thin shock transition layer. The shock jump conditions, to be discussed later in the course, deter- mine the temperature and density behind a shock; the entropy always increases across a shock. Shocks are believed to dominate the heating of the hot component of the ISM (the hot ionized medium, or HIM). - Turbulent heating: The ISM is observed to have substantial bulk motions that are believed to be turbulent. If the velocity on a scale ` is v(`), then the characteristic damping time for these motions is the dynamical time `=v(`). The heating rate per unit mass is then ¡ v(`)2=2 v(`)3 » = : (9) ¹H `=v(`) 2` The actual heating mechanism is that the motions cascade to smaller and smaller scales until they are dissipated by viscosity. It follows that the heating rate is independent of scale ` so that v(`) / `1=3, as ¯rst shown by Kolmogorov. Turbulence in the ISM is complicated by the fact that it is magnetized and can be supersonic, but the Kolmogorov relation remains approximately valid. The importance of turbulent heating in the ISM is under active investigation. Cosmic ray heating: - High energy particles permeate the ISM, and we can observe those that are able to penetrate through the solar wind to reach the Earth or spacecraft in the solar system. These particles ionize atoms, and the ejected electrons heat the gas. We shall discuss this further when we talk about cosmic rays in more detail. Magnetic heating { 4 { - Reconnection: The magnetic energy in the ISM is comparable to or greater than the thermal energy. If this energy can be dissipated, it can be a signi¯cant heat source. In ionized components of the ISM, the ¯eld is \frozen" to the plasma and cannot directly heat it. However, on su±ciently small scales, flux freezing breaks down and the topology of the ¯eld can be altered by magnetic reconnection. Reconnection is observed in the Sun and in the Earth's magnetosphere. Energy goes both into heat and into bulk motions, but the process is not well understood. - Ambipolar di®usion: The magnetic ¯eld is directly coupled to the ionized component of the gas, which in turn is coupled to the neutral component only through collisions. If the drift velocity between the neutral and ionized components is signi¯cant, as it can be in the weakly ionized gas in molecular clouds, then this process can lead to signi¯cant heating. Next we consider the cooling processes, which are only three in number: Collisional excitation (bound-bound): - Particle collisions (electrons, atoms or molecules impinging on atoms or molecules) can excite internal degrees of freedom which can then decay by radiative emission. This is the dominant cooling process in the ISM. Recombination cooling (bound-free). - When an electron recombines with an ion, an energy ee; rec + I, where I is the ionization energy, is radiated. In Case A, the radiation escapes from the gas, and the recombination (1) coe±cient is written as ®A or ® , indicating that recombinations to all states are e®ective. In Case B, photons arising from recombinations to the ground state photoionize other atoms and do not escape; as a result, only recombinations to excited states result in a net recombination.
Load more

Recommended publications
  • Contents • Introduction to Proteomics and Mass Spectrometry
    Contents • Introduction to Proteomics and Mass spectrometry - What we need to know in our quest to explain life - Fundamental things you need to know about mass spectrometry • Interfaces and ion sources - Electrospray ionization (ESI) - conventional and nanospray - Heated nebulizer atmospheric pressure chemical ionization - Matrix assisted laser desorption • Types of MS analyzers - Magnetic sector - Quadrupole - Time-of-flight - Hybrid - Ion trap In the next step in our quest to explain what is life The human genome project has largely been completed and many other genomes are surrendering to the gene sequencers. However, all this knowledge does not give us the information that is needed to explain how living cells work. To do that, we need to study proteins. In 2002, mass spectrometry has developed to the point where it has the capacity to obtain the "exact" molecular weight of many macromolecules. At the present time, this includes proteins up to 150,000 Da. Proteins of higher molecular weights (up to 500,000 Da) can also be studied by mass spectrometry, but with less accuracy. The paradigm for sequencing of peptides and identification of proteins has changed – because of the availability of the human genome database, peptides can be identified merely by their masses or by partial sequence information, often in minutes, not hours. This new capacity is shifting the emphasis of biomedical research back to the functional aspects of cell biochemistry, the expression of particular sets of genes and their gene products, the proteins of the cell. These are the new goals of the biological scientist: o to know which proteins are expressed in each cell, preferably one cell at a time o to know how these proteins are modified, information that cannot necessarily be deduced from the nucleotide sequence of individual genes.
    [Show full text]
  • Mass Spectrometry (Technically Not Spectroscopy)
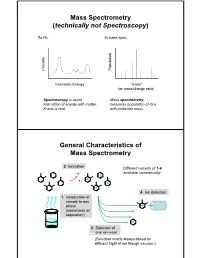
    Mass Spectrometry (technically not Spectroscopy) So far, In mass spec, on y Populati Intensit Excitation Energy “mass” (or mass/charge ratio) Spectroscopy is about Mass spectrometry interaction of energy with matter. measures population of ions X-axis is real. with particular mass. General Characteristics of Mass Spectrometry 2. Ionization Different variants of 1-4 -e- available commercially. 4. Ion detection 1. Introduction of sample to gas phase (sometimes w/ separation) 3. Selection of one ion mass (Selection nearly always based on different flight of ion though vacuum.) General Components of a Mass Spectrometer Lots of choices, which can be mixed and matched. direct injection The Mass Spectrum fragment “daughter” ions M+ “parent” mass Sample Introduction: Direc t Inser tion Prob e If sample is a liquid, sample can also be injected directly into ionization region. If sample isn’t pure, get multiple parents (that can’t be distinguished from fragments). Capillary Column Introduction Continous source of molecules to spectrometer. detector column (including GC, LC, chiral, size exclusion) • Signal intensity depends on both amount of molecule and ionization efficiency • To use quantitatively, must calibrate peaks with respect eltilution time ttlitotal ion curren t to quantity eluted (TIC) over time Capillary Column Introduction Easy to interface with gas or liquid chromatography. TIC trace elution time time averaged time averaged mass spectrum mass spectrum Methods of Ionization: Electron Ionization (EI) 1 - + - 1 M + e (kV energy) M + 2e Fragmentation in Electron Ionization daughter ion (observed in spectrum) neutral fragment (not observed) excited parent at electron at electron energy of energy of 15 eV 70 e V Lower electron energy yields less fragmentation, but also less signal.
    [Show full text]
  • An Introduction to Mass Spectrometry
    An Introduction to Mass Spectrometry by Scott E. Van Bramer Widener University Department of Chemistry One University Place Chester, PA 19013 [email protected] http://science.widener.edu/~svanbram revised: September 2, 1998 © Copyright 1997 TABLE OF CONTENTS INTRODUCTION ........................................................... 4 SAMPLE INTRODUCTION ....................................................5 Direct Vapor Inlet .......................................................5 Gas Chromatography.....................................................5 Liquid Chromatography...................................................6 Direct Insertion Probe ....................................................6 Direct Ionization of Sample ................................................6 IONIZATION TECHNIQUES...................................................6 Electron Ionization .......................................................7 Chemical Ionization ..................................................... 9 Fast Atom Bombardment and Secondary Ion Mass Spectrometry .................10 Atmospheric Pressure Ionization and Electrospray Ionization ....................11 Matrix Assisted Laser Desorption/Ionization ................................ 13 Other Ionization Methods ................................................13 Self-Test #1 ...........................................................14 MASS ANALYZERS .........................................................14 Quadrupole ............................................................15
    [Show full text]
  • Methods of Ion Generation
    Chem. Rev. 2001, 101, 361−375 361 Methods of Ion Generation Marvin L. Vestal PE Biosystems, Framingham, Massachusetts 01701 Received May 24, 2000 Contents I. Introduction 361 II. Atomic Ions 362 A. Thermal Ionization 362 B. Spark Source 362 C. Plasma Sources 362 D. Glow Discharge 362 E. Inductively Coupled Plasma (ICP) 363 III. Molecular Ions from Volatile Samples. 364 A. Electron Ionization (EI) 364 B. Chemical Ionization (CI) 365 C. Photoionization (PI) 367 D. Field Ionization (FI) 367 IV. Molecular Ions from Nonvolatile Samples 367 Marvin L. Vestal received his B.S. and M.S. degrees, 1958 and 1960, A. Spray Techniques 367 respectively, in Engineering Sciences from Purdue Univesity, Layfayette, IN. In 1975 he received his Ph.D. degree in Chemical Physics from the B. Electrospray 367 University of Utah, Salt Lake City. From 1958 to 1960 he was a Scientist C. Desorption from Surfaces 369 at Johnston Laboratories, Inc., in Layfayette, IN. From 1960 to 1967 he D. High-Energy Particle Impact 369 became Senior Scientist at Johnston Laboratories, Inc., in Baltimore, MD. E. Low-Energy Particle Impact 370 From 1960 to 1962 he was a Graduate Student in the Department of Physics at John Hopkins University. From 1967 to 1970 he was Vice F. Low-Energy Impact with Liquid Surfaces 371 President at Scientific Research Instruments, Corp. in Baltimore, MD. From G. Flow FAB 371 1970 to 1975 he was a Graduate Student and Research Instructor at the H. Laser Ionization−MALDI 371 University of Utah, Salt Lake City. From 1976 to 1981 he became I.
    [Show full text]
  • Selective Chemical Ionization of Nitrogen and Sulfur Heterocycles in Petroleum Fractions by Ion Trap Mass Spectrometry
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector Selective Chemical Ionization of Nitrogen and Sulfur Heterocycles in Petroleum Fractions by Ion Trap Mass Spectrometry C. S. Creaser*, F. Krokos, and K. E. O’Neill Shod of Chemical Sciences, University of East Anglia, Norwich, United Kingdom M. J. C. Smith and P. G. McDowell BP Research, Sunbury-on-Thames, Middlesex, United Kingdom A procedure is reported for the selective ammonia chemical ionization of some nitrogen and sulfur heterocycles in petroleum fractions using ion trap mass spectrometry (ITMS). The ion trap scan routine is designed to optimize the population of ammonium reagent ions and eject from the trap (by radio frequency/direct current isolation) electron ionization products formed during reagent ion formation prior to ionization of the sample. The ITMS procedure is compared with standard ion trap detector and conventional quadrupole ammonia chemi- cal ionization for the determination of nitrogen and sulfur heterocycles in gas oil and kerosine samples. Greatly enhanced selectivity is shown for the ITMS procedure by sup res- sion of competing charge-exchange processes. (1 Am Sot Mass Spectrum 1993, 4, 322-326 ‘; he removal of organic compounds containing reagent ion NH;, is formed via the reactions [5] nitrogen and sulfur is an important part of the T petroleum-refining process 111. Their presence in NH, ‘1 NH;’ (1) petroleum distillates results in the formation of envi- NH, f NH:‘+ NH; + NH; (2) ronmental pollutants (SO,, NO,) during combustion, and their reactivity can lead to catalyst poisoning Whereas NH: is unreactive toward a wide range of in refinery processes.
    [Show full text]
  • Using Collision-Induced Dissociation Techniques to Constrain
    Geophysical Research Abstracts Vol. 21, EGU2019-8406, 2019 EGU General Assembly 2019 © Author(s) 2019. CC Attribution 4.0 license. Using collision-induced dissociation techniques to constrain sensitivities of + ammonia chemical ionization mass spectrometry (NH4 − CIMS) to oxygenated organic compounds in the gas and particle phases Frank Keutsch (1,2,3), Alexander Zaytsev (1), Martin Breitenlechner (1), Abigail Koss (4), Christopher Lim (4), James Rowe (4), and Jesse Kroll (4) (1) School of Engineering and Applied Sciences, Harvard University, Cambridge, United States, (2) Department of Chemistry & Chemical Biology, Harvard University, Cambridge, United States, (3) Department of Earth and Planetary Sciences, Harvard University, Cambridge, United States, (4) Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, United States Chemical ionization mass spectrometry (CIMS) has become an important analytical tool for measurements of organic molecules in the atmosphere. A variety of reagent ions can be used to detect different classes of volatile or- ganic compounds (VOCs) and to analyze submicrometer particulate organic matter. However, detection efficiency and sensitivity of CIMS instruments depend critically on both the reagent ion and the measured sample molecule. We have developed a new CIMS instrument that is equipped with three similar corona discharge ion sources and currently can be operated in two different modes: (1) ligand switching reactions from adduct ions + + + NH4 •(H2O)n; (n = 0; 1; 2)(NH4 −CIMS) and (2) proton transfer reactions with H3O •(H2O)n; (n = 0; 1) ions (PTR − MS). We present a mass spectrometric voltage scanning procedure which is based on collision- induced dissociation that allows for the determination of the stability of detected ammonium-organic clusters.
    [Show full text]
  • Gas-Phase Ion Chemistry: Kinetics and Thermodynamics
    Gas-Phase Ion Chemistry: Kinetics and Thermodynamics by Charles M. Nichols B. S., Chemistry – ACS Certified University of Central Arkansas, 2009 A thesis submitted to the Faculty of the Graduate School of the University of Colorado in partial fulfillment of the requirements for the degree of Doctor of Philosophy Department of Chemistry and Biochemistry 2016 This thesis entitled: Gas-Phase Ion Chemistry: Kinetics and Thermodynamics Written by Charles M. Nichols has been approved for the Department of Chemistry and Biochemistry by: _______________________________________ Veronica M. Bierbaum _______________________________________ W. Carl Lineberger Date: December 08, 2015 A final copy of this thesis has been examined by all signatories, and we find that both the content and the form meet acceptable presentation standards of scholarly work in the above mentioned discipline. Nichols, Charles M. (Ph.D., Physical Chemistry) Gas Phase Ion Chemistry: Kinetics and Thermodynamics Thesis directed by Professors Veronica M. Bierbaum and W. Carl Lineberger Abstract: This thesis employs gas-phase ion chemistry to study the kinetics and thermodynamics of chemical reactions and molecular properties. Gas-phase ion chemistry is important in diverse regions of the universe. It is directly relevant to the chemistry occurring in the atmospheres of planets and moons as well as the molecular clouds of the interstellar medium. Gas-phase ion chemistry is also employed to determine fundamental properties, such as the proton and electron affinities of molecules. Furthermore, gas-phase ion chemistry can be used to study chemical events that typically occur in the condensed-phase, such as prototypical organic reactions, in an effort to reveal the intrinsic properties and mechanisms of chemical reactions.
    [Show full text]
  • Applications of Air Ionization for Control of Vocs and Pmx WHITE PAPER February 28, 2019
    Applications of Air Ionization for Control of VOCs and PMx WHITE PAPER February 28, 2019 www.globalplasmasolutions.com © 2020 Global Plasma Solutions, Inc. ® GPS, Global Plasma Solutions and its logos are registered trademarks of Global Plasma Solutions, Inc. Applications of Air Ionization for Control of VOCs and PMX Paper # 918 (Session AB-7a: Advances in, and Evaluation of, IAQ Control. Dr. Stacy L. Daniels Director of Research, Precision Air, a Division of Quality Air of Midland, Inc. 3600 Centennial Drive, Midland, MI 48642 ABSTRACT Recent developments in the application of controllable air ionization processes have led to significant reductions in airborne microbials, neutralization of odors, and reductions of specific volatile organic compounds (VOCs) in the indoor air environment. Removal of very fine particulates (PMx) by conventional HEPA filters also is enhanced by air ionization. The process of air ionization involves the electronically induced formation of small air ions, including superoxide O2 .-, i.e. the diatomic oxygen radical anion, which react rapidly with airborne VOC and PMx species. The significance of air ionization chemistry and its potential for contributing to significant improvements in Indoor Air Quality will be discussed using case histories. INTRODUCTION Air Ionization: Where We’re Coming From … “Although the electrical discharge in gases has been investigated in its various phases ever since the study of electricity itself began, it is only in the last five or six years that our knowledge of the subject has begun to take systematic and satisfactory form. Careful observations has been made by hundreds of physicists, and the scientific literature abounded with descriptions of phenomena of great interest and undoubted scientific importance.
    [Show full text]
  • Online Atmospheric Pressure Chemical Ionization Ion Trap Mass Spectrometry
    EGU Journal Logos (RGB) Open Access Open Access Open Access Advances in Annales Nonlinear Processes Geosciences Geophysicae in Geophysics Open Access Open Access Natural Hazards Natural Hazards and Earth System and Earth System Sciences Sciences Discussions Open Access Open Access Atmospheric Atmospheric Chemistry Chemistry and Physics and Physics Discussions Open Access Open Access Atmos. Meas. Tech., 6, 431–443, 2013 Atmospheric Atmospheric www.atmos-meas-tech.net/6/431/2013/ doi:10.5194/amt-6-431-2013 Measurement Measurement © Author(s) 2013. CC Attribution 3.0 License. Techniques Techniques Discussions Open Access Open Access Biogeosciences Biogeosciences Discussions Open Access Online atmospheric pressure chemical ionization ion trap mass Open Access n spectrometry (APCI-IT-MS ) for measuring organic acidsClimate in Climate of the Past of the Past concentrated bulk aerosol – a laboratory and field study Discussions A. L. Vogel1, M. Aij¨ al¨ a¨2, M. Bruggemann¨ 1, M. Ehn2,*, H. Junninen2, T. Petaj¨ a¨2, D. R. Worsnop2, M. Kulmala2, Open Access 3 1 Open Access J. Williams , and T. Hoffmann Earth System 1Institute of Inorganic Chemistry and Analytical Chemistry, Johannes Gutenberg-UniversityEarth Mainz, System 55128 Mainz, Germany 2Department of Physics, University of Helsinki, 00014 Helsinki, Finland Dynamics Dynamics 3Department of Atmospheric Chemistry, Max Planck Institute for Chemistry, 55128 Mainz, Germany Discussions *now at: IEK-8: Troposphere, Research Center Julich,¨ 52428 Juelich, Germany Open Access Correspondence to: T. Hoffmann ([email protected]) Geoscientific Geoscientific Open Access Instrumentation Instrumentation Received: 15 August 2012 – Published in Atmos. Meas. Tech. Discuss.: 30 August 2012 Revised: 21 January 2013 – Accepted: 25 January 2013 – Published: 20 February 2013 Methods and Methods and Data Systems Data Systems Discussions Open Access Abstract.
    [Show full text]
  • 5973A/N Setting up Chemical Ionization Methane Reagent Gas Flow
    Setting up Chemical Ionization Methane reagent gas flow Applies to 5973A/N Mass Spec Caution: Always verify MSD system performance in EI (Electron Impact) before switching to CI (Chemical Ionization) mode of operation. Always set up the CI MSD in PCI (Positive Chemical Ionization) first, “using Methane”, even if you're planning to run in the NCI (Negative Chemical Ionization) mode. To set up methane reagent gas flow for CI operation: The reagent gas flow must be adjusted for maximum stability before tuning the CI system. Perform the initial setup with methane as your reagent gas in the positive ion mode (PCI). There is no flow adjustment procedure available for the negative ionization mode (NCI), as there are no negative reagent ions formed. Adjusting the methane reagent gas flow is a three (3) step process: 1. Setting the flow control. 2. Pre-tuning on the reagent gas ions. 3. Adjusting the flow for reagent gas ion ratios for methane, m/z 28 / 27. Your data system will prompt you through the flow adjustment procedures. Caution: After the system has been switched from EI to CI mode, or vented for any other reason, the MSD must be baked out for at least 2 hours before tuning. This document is believed to be accurate and up-to-date. However, Agilent Technologies, Inc. cannot assume responsibility for the use of this material. The information contained herein is intended for use by informed individuals who can and must determine its fitness for their purpose. A20737.doc http:// www.chem.agilent.com Page 1 of 2 Setting up Methane gas flow: 1.
    [Show full text]
  • Negative Ion Chemical Ionization (NCI) Studies Using the Thermo Scientific ISQ 7000 Singe Quadrupole GC-MS System
    TECHNICAL NOTE 10654 Negative Ion Chemical Ionization (NCI) studies using the Thermo Scientific ISQ 7000 single quadrupole GC-MS system Author Goal Amit Gujar To demonstrate NCI capabilities of the Thermo ScientificTM ISQTM 7000 single Thermo Fisher Scientific, quadrupole GC-MS system with methane reagent gas, attainable typical Austin, TX, USA instrument detection limits (IDLs), and the effect of the ion source temperature and reagent gas flow rates on NCI mass spectra. Keywords Introduction Negative ion chemical Negative ion chemical ionization (NICI or NCI) is a popular ionization ionization (NICI or NCI), IDL, technique for gas chromatography-mass spectrometry (GC-MS) that is Octafluoronaphthalene, ISQ frequently used for analyzing electrophilic molecules of environmental 7000, gas chromatography-mass concern such as brominated flame retardants (BFR)1 and chlorinated spectrometry pesticides.2 It is also a popular technique in steroid and drug analysis after derivatization of the analyte with compounds that add electronegative atoms to the molecule.3 The advantages the NCI technique offers are high sensitivity and selectivity for electrophilic molecules in complex matrices. Electron capture (as opposed to true negative ionization involving high energy electron-molecule reaction) is the main mechanism in formation of negative ions in the mass spectrometry technique as shown below.4 AB + e- (~0.1 eV) ABˉ˙ (Resonance electron capture) AB + e- (0-15 eV) � A˙ + Bˉ (Dissociative electron capture) AB + e- (>10 eV) �Aˉ + B+ + e- (Ion-pair formation) � This is why NCI is also referred to as electron capture This technical note provides details on the methane-NCI negative ionization (ECNI). ECNI results from resonance capability of the ISQ 7000 single quadrupole GC- capture of low-energy (thermalized) secondary electrons MS system.
    [Show full text]
  • Introduction to Chemical Ionization & Instrumentation
    4/23/2015 1 Introduction to Chemical Ionization & Instrumentation Advanced Atmospheric chemistry CHEM-5152 Spring 2015 Prof. J.L. Jimenez 2 Chemical Ionization (CI) Introduced in 1966 by Munson and Field1, it was a direct outgrowth of fundamental studies of ion/molecule interactions. Where other techniques rely on interaction of molecule and electron, photon, or electric field, ionization of the analyte molecule, M, is achieved through reaction with a reagent ion, R+ CI Method of Munson & Field (Still used) 1. Reagent species is ionized by high-pressure* electron ionization e- + R → R+ + 2 e- 2. Collision of reagent ion with gas-phase analyte (present at <1% abundance of reagent) yields analyte ion + + R + M → M1 + R1 3. Potential fragmentation of M+ by one or more pathways + → + → + M1 M2 + N2 M3 + N3 → + M4 + N4 *: how high P? Remember prob of an electron leading to ionization is ~3 x 10-7 at P = 10-7 Torr 1. Munson and Field, JACS, 2621, 1966. – Suggested reading on course web page 1 4/23/2015 3 Solvation in IMRs From Hoffmann 4 Efficiency of IMRs • Approx. every collision leads to a proton transfer, if G0 < 0 From Hoffmann 2 4/23/2015 5 CI Ion Source From Barker Similar to EI source. •Higher P •Simultaneous introduction of M and R 6 Proton transfer reaction – mass spectrometry H3O VOC VOCH H2O PA(VOC) > PA(H2O) Courtesy of Lisa Kaser, NCAR 3 4/23/2015 Potential Complexity of Reagent Ions - + - CH + CH4 + e CH4 + 2e 5 + + + CH4 + CH4 CH5 + CH3 C2H5 + + CH4 CH3 + H + + CH4 CH2 + H2 + C3H5 + + CH3 + CH4 C2H5 + H2 + + CH2 + CH4 C2H3 + H2 + H + + C2H3 + CH4 C3H5 + H2 Relevant reaction: + + CH4 + H → CH5 -1 PA(CH4) = -∆H = 131 kcal mol Relevant reaction: + + C2H4 + H → C2H5 PA(C H ) = -∆H = 162.6 kcal mol-1 2 4 7 8 Selected Ion Flow Tube & SYFT MS 1.
    [Show full text]