DOCSLIB.ORG

A Coherent Nanotube Oscillator Driven by Electromechanical Backaction Edward Laird a Coherent Nanotube Oscillator Driven by Electromechanical Backaction

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
A Coherent Nanotube Oscillator Driven by Electromechanical Backaction Edward Laird a Coherent Nanotube Oscillator Driven by Electromechanical Backaction 1 A coherent nanotube oscillator driven by electromechanical backaction Edward Laird A coherent nanotube oscillator driven by electromechanical backaction Yutian Wen Natalia Ares Tian Pei Felix Schupp Andrew Briggs (at Oxford) ERC Consolidator Grant Panel 2016 Members of the ERC Peer Review Panels European Microkelvin The list below includes the panel members in the ERC Consolidator Grant 2016 peer review process, identified and invited by the ERC Scientific Council. There are in total 25 panels, divided Platform between the three domains as follows: 9 panels in Life Sciences (LS), 10 panels in Physical Sciences and Engineering (PE), and 6 panels in Social Sciences and Humanities (SH). 2 Panel chairs appear at the top of each panel list, followed by panel members in alphabetical order. Note to applicants: This information is given for reasons of transparency. Under no circumstances should peer reviewers be contacted by applicants, potential applicants or potential host institutions. Questions can be addressed to: - ERC Helpdesk http://ec.europa.eu/research/index.cfm?lg=en&pg=enquiries - ERC National Contact Points http://erc.europa.eu/ncp ERC- 2016-CoG Panel Members List – Release date: 01/02/2017 The limits of displacement sensing Suspended carbon nanotube ~106 nucleons Diameter ~5 nm Length ~800 nm • High mechanical quality factor • High frequency (200 MHz ≡ 10 mK) • Mechanically compliant • Can be integrated into electronic circuits 3 The limits of displacement sensing: Magnetic resonance microscopy Force per proton: ~10-20 N Review: Poggio & Harzheim (2018) 4 A coherent nanotube oscillator driven by electromechanical backaction 1. Measuring vibrations with a single-electron transistor 2. Creating a nanomechanical oscillator 3. Characterizing the oscillator 5 Question 1: How precisely can we measure nanomechanical vibrations? Standard quantum limit for continuous measurements (m/√Hz): Quality factor Mechanical frequency Theory: Caves et al. (RMP 1982) Mass Experiment: LaHaye et al. (Science 2004) Review: Clerk et al. (RMP 2010) 6 Question 2: Can we make a laser for sound? Microwave amplification by stimulated emission of radiation (Townes, 1955) 7 A vibrating carbon nanotube device Laird et al (2011) ~2 nm 1 µm 8 The single-electron transistor Energy levels ) nA Current ( Current Gate voltage (V) Hüttel et al (van der Zant group, 2009) 9 Sensing vibrations Motion Current Displacement Hüttel et al (2009) 10 Fast readout for nanotube vibrations SiGe amplifier Details: Wen et al. (2018) Schupp et al. (2018) 11 How precisely can we measure nanomechanical vibrations? 12 Is this a laser analogue? 13 REPORTS tions do not simply smooth the stepwise (G ~ f0), damping of the mechanical motion is addition to the overall softening of k yielding the transition from the static single-electron tuning minimized, and we observe the highest value of frequency dips of Fig. 2, the fluctuating charge on shifts. Instead, fluctuations caused dips in the Q.OnaCoulombpeak,chargefluctuationsare the dot also changes a,givingasofteningspring resonant frequency up to one order of magnitude maximized (G >> f0), and Q decreases to a few (a <0)outsideofthefrequencydip(Coulomb greater than the single-electron tuning shifts. As thousand. These results explicitly show that detec- valleys) and a hardening spring (a >0)insidethe shown in (13, 22)anddiscussedindetailinthe tor back-action can cause substantial mechanical frequency dip (Coulomb peaks), as shown in Fig. supporting online material (SOM) (20), the dy- damping. The underlying mechanism for the damp- 3. The sign of a follows the curvature of f0(Vg) namic force modifies the nanotube’sspringcon- ing is an energy transfer occasionally occurring induced by the fluctuating electron force, giving a stant (k)resultinginasofteningofthemechanical when a current-carrying electron is pushed up to change in sign at the inflection point of the fre- resonance. The shape of the frequency dip can be ahigher(electrostatic)energybythenanotube quency dip. Nonlinearity from the single-electron altered by applying a finite bias (Vsd)acrossthe motion before tunneling out of the dot. This gain force in our device dominates and is much stronger nanotube. Starting from deep and narrow at small in potential energy is later dissipated in the drain than that from the mechanical deformation (20). Vsd =0.5mV,thedipbecomesshallowerand contact. Figure 3, E and F, shows the regime of further broader with increasing Vsd.Thisdipshapelargely If we drive the system at higher RF powers enhanced RF driving. Now the nonlinearity is no resembles the broadening of Coulomb blockade (Fig. 3, C and D), we observe an asymmetric longer a perturbation of the spring constant, but peaks that occurs with increasing Vsd.Thus,we resonance peak, along with distinct hysteresis be- instead gives sharp peaks in the line shape and conclude from Fig. 2 that the single-electron tween upward and downward frequency sweeps. switching between several different metastable tuning oscillations are a mechanical effect that is Theoretically, this marks the onset of nonlinear modes [see further data in the SOM (20)]. At this adirectconsequenceofsingle-electrontunneling terms in the equation of motion, such as in the strong driving, we observe highly structured non- oscillations. well-studied Duffing oscillator (23, 24). k is mod- linear mechanical behavior that arises from the Besides softening, the charge fluctuations also ified by a large oscillation amplitude (x)thatis coupling of the resonator motion to the quantum provide a channel for dissipation of mechanical accounted for by replacing k with (k + ax2). The dot. energy. Figure 3A shows the resonance dip for time-averaged spring constant increases if a >0, In Fig. 3, we studied nonlinear coupling be- small RF power, with frequency traces in Fig. 3B. which is accompanied by a sharp edge at the high- tween the quantum dot and the mechanical res- In the Coulomb valleys, tunneling is suppressed frequency side of the peak; vice versa for a <0.In onator by applying a large RF driving force at a on April 26, 2010 Fig. 4. Spontaneous driving 05dI/dV (µS) 0 -10 dI/dV (µS) 5 Evidence for self-driven oscillations of the mechanical resonance sd by single-electron tunneling. A B D I (A)Differentialconductance 2 (dI/dVsd)showingridgesof 10 5 sharp positive (deep red) and (nA) sd negative (deep blue) spikes (ar- I B rows). ( )Similarridgesmea- ) sured on device two (trench Gate voltage-4.93 Vg nA www.sciencemag.org width = 430 nm) in the few- (mV) 5 (mV) 5 sd sd – – V hole regime (four-hole to V three-hole transition). Spikes in dI/dVsd appear as steplike ridges in current. (C)shows -10 Current ( the data from the upper half Self-oscillation of (B), but now as a three- -2 dimensional current plot. The threshold 0 0 ridges are entirely reproduc- Downloaded from ible. (D)(Inset)Coulombpeak -5.19 V (V) -5.17 -1.05 V (V) -0.95 Gate voltage g g E at V =0.5mVshowinglarge sd 284.5 switching-steps. (Main plot) From Steele et al (Kouwenhoven group, 2009) 14 Zoom-in view on data from C inset. (E)RFdrivenmechanical resonance measured for the 10 nA same Coulomb peak in (D) at adrivingpowerof–50 dB. Outside the switch region, the resonance has a narrow line shape and follows the soften- I f (MHz) ing dip from Figs. 2 and 3. At sd the first switch, the resonance position departs from the 283.5 expected position (indicated by dashed line). The mechan- 0.5 ical signal is strongly enhanced (nA) in amplitude and displays a sd I V ∆ broad asymmetric line shape. V sd At the second switch, the res- g -0.75 onance returns to the frequency -4.935 -4.93 Vg (V) and narrow line shape expected at these powers. 1106 28 AUGUST 2009 VOL 325 SCIENCE www.sciencemag.org A coherent nanotube oscillator driven by electromechanical backaction 1. Measuring vibrations with a single-electron transistor 2. Creating a nanomechanical oscillator 3. Characterizing the oscillator 15 Excitation off Bias on, excitation on Gate voltage (mV) Bias on, excitation off A coherent nanotube oscillator driven by electromechanical backaction 1. Measuring vibrations with a single-electron transistor 2. Creating a nanomechanical oscillator 3. Characterizing the oscillator 17 Measuring the output coherence 18 Statistics of the output coherence Emission histograms Correlation function 19 How the oscillator works Electrical charge Electrical Bennet & Clerk (2007) Usmani, Blanter, Nazarov (2007) 20 How the oscillator works Electrical charge Electrical Bennet & Clerk (2007) Usmani, Blanter, Nazarov (2007) 21 Laser physics I: Injection locking Principle Implementation Discovery: Huygens (1666) In lasers: Stover and Steier (1966) 22 Laser physics I: Injection locking 23 Laser physics II: Stabilising using feedback 24 Laser physics II: Stabilising using feedback 25 Why are nanomechanical lasers interesting? • They connect the physics of backaction with the physics of lasers. • They are amplifiers and transducers. Narrow linewidth means better sensitivity to perturbations. • They are on-chip phonon generators for microscopy, information transfer, etc. • They couple charge and motion on a mesoscopic scale. 26 Other nano-oscillators NATURE COMMUNICATIONS | DOI: 10.1038/ncomms2827 Electrical ARTICLE Spin transfer torque Double quantum dot micromaser Josephson laser (Pribiag 2007) (Liu 2017) (Cassidy 2017) elf-sustained oscillations (SSOs) are distinct from the forced B I motion of a resonator because the oscillation period does bias Snot depend on the frequency of the driving force. Resonators in the SSO regime typically produce signals with a F J spectral line width, which is narrower than the intrinsic line L u VLF VHF width of the resonator. The reduced line width enhances the Φa 1 ! sensitivity of resonance-based force-gradient sensors . On the 1 !2 other hand, these oscillations are not desirable in experiments I Mechanical that require observation of very small displacements, such as bias those induced by gravitational waves2 and quantum-mechanical Optomechanics 3–5 Optomechanics Vibrating SQUID (Grudininzero-point2010) fluctuations .
Load more

Recommended publications
  • GALLIUM OXIDE METAL OXIDE SEMICONDUCTOR FIELD EFFECT TRANSISTOR ANALYTICAL MODELING and POWER TRANSISTOR DESIGN TRADES By
    GALLIUM OXIDE METAL OXIDE SEMICONDUCTOR FIELD EFFECT TRANSISTOR ANALYTICAL MODELING AND POWER TRANSISTOR DESIGN TRADES by Neil Austin Moser A Dissertation Submitted to the Graduate Faculty of George Mason University in Partial Fulfillment of The Requirements for the Degree of Doctor of Philosophy Electrical and Computer Engineering Committee: _________________________________ Dr. Nathalia Peixoto, Dissertation Director _________________________________ Dr. Qiliang Li, Committee Member _________________________________ Dr. Yuri Mishin, Committee Member _________________________________ Dr. Gregg Jessen, Committee Member _________________________________ Dr. Monson Hayes, Department Chair _________________________________ Dr. Kenneth S. Ball, Dean, Volgenau School of Engineering Date:_____________________________ Fall Semester 2017 George Mason University Fairfax, VA Gallium Oxide Metal Oxide Semiconductor Field Effect Transistor Analytical Modeling and Power Transistor Design Trades A Dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy at George Mason University by Neil Austin Moser Master of Science George Mason University, 2013 Bachelor of Science University of Michigan-Ann Arbor, 2002 Director: Nathalia Peixoto, Professor Department of Electrical and Computer Engineering Fall Semester 2017 George Mason University Fairfax, VA Copyright 2017 Neil Austin Moser All Rights Reserved ii DEDICATION This is dedicated to my father, Gary Moser, who started me on the path to being an academic before I even really knew what that was and still encourages me to not be ignorant about anything to this day. iii ACKNOWLEDGEMENTS I would like to thank my wife, Morgan, and daughter, Schaefer, for putting up with me “working” on this for quite a long time. Also, I would like to thank my committee, especially Gregg Jessen who helped me find this exciting research and shepherded me the whole way and Nathalia Peixoto who put up with a lot of dead ends and redirections in topic along the way.
    [Show full text]
  • A Nanoscale Study of Mosfets Reliability and Resistive Switching in RRAM Devices
    ADVERTIMENT. Lʼaccés als continguts dʼaquesta tesi queda condicionat a lʼacceptació de les condicions dʼús establertes per la següent llicència Creative Commons: http://cat.creativecommons.org/?page_id=184 ADVERTENCIA. El acceso a los contenidos de esta tesis queda condicionado a la aceptación de las condiciones de uso establecidas por la siguiente licencia Creative Commons: http://es.creativecommons.org/blog/licencias/ WARNING. The access to the contents of this doctoral thesis it is limited to the acceptance of the use conditions set by the following Creative Commons license: https://creativecommons.org/licenses/?lang=en Universitat Autònoma de Barcelona Escola d’Enginyeria Electronic Engineering Department A nanoscale study of MOSFETs reliability and Resistive Switching in RRAM devices A dissertation submitted by Qian Wu in fulfillment of the requirements for the Degree of Doctor of Philosophy in Electronic and Telecommunication Engineering Supervised by Dr. Marc Porti i Pujal Bellaterra, November 2016 Universitat Autònoma de Barcelona Escola d’Enginyeria Electronic Engineering Department Dr. Marc Porti i Pujal, associate professor of the Electronic Engineering Department of the Universitat Autònoma de Barcelona, Certifies That the dissertation: A nanoscale study of MOSFETs reliability and Resistive Switching in RRAM devices submitted by Qian Wu to the School of Engineering in fulfillment of the requirements for the Degree of Doctor in the Electronic and Telecommunication Engineering Program, has been performed under his supervision. Dr. Marc Porti Bellaterra, November of 2016 To my family Acknowledgement The four years’ doctoral study is a significant and unforgettable experience for me. Many kind-hearted people give me a great amount of help, professional advice and encouragement.
    [Show full text]
  • Custom Design of Monolithic Microwave Integrated Circuits
    CRAIG R. MOORE and JOHN E. PENN CUSTOM DESIGN OF MONOLITHIC MICROWAVE INTEGRATED CIRCUITS Monolithic microwave integrated circuits (MMIC'S) have been designed at the Applied Physics Laboratory and fabricated at several gallium arsenide foundries since 1989. The design tools and methods for designing MMIC'S have evolved to the present use of integrated computer-aided engineering software with programmable design components. Software elements that can be customized create multilayer mask descriptions of components for transistors, resistors, capacitors, inductors, microstrip connections, and other structures to improve the quality and productivity of MMIC's designed at the Laboratory. The schematic, physical layout, and simulation models are integrated into a single software tool, eliminating much potential for error. Experience with various foundries and various MMIC design techniques have increased our ability to design at higher and higher frequencies with confidence in achieving first-time success. The design improvements have been accompanied by improvements in measurement techniques for higher frequencies using microwave probe stations. This article summarizes MMIC designs at the Laboratory over the past few years and the progress shown and lessons learned. COMPUTER-AIDED ENGINEERING DESIGN OF MMIC'S Software computer-aided engineering tools from and custom electrical models. Today, EEsof has a new EEsof, Inc., are the predominant means of designing TriQuint Smart Library containing physical and electrical monolithic microwave integrated circuits (MMIC'S) at APL. macros, which is being used in the MMIC design course A key feature of EEsof's Academy software for MMIC at JHU taught by both authors of this article. layout is the ease of adding both layout macros and A group of people including Dale Dawson of Westing­ custom electrical models.
    [Show full text]
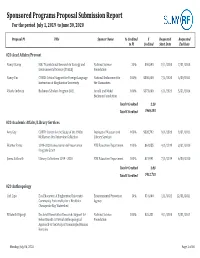
  • Sponsored Programs Proposal Submission Report for the Period July 1, 2019 to June 30, 2020
    Sponsored Programs Proposal Submission Report For the period July 1, 2019 to June 30, 2020 Proposal PI Title Sponsor Name % Credited $ Requested Requested to PI Credited Start Date End Date 020 Acad Affairs/Provost Nancy Stamp IGE: Translational Research in Ecology and National Science 20% $96,593 8/1/2020 7/31/2023 Environmental Science (TREES) Foundation Nancy Um COVID: Critical Support for Foreign Language National Endowment for 100% $300,000 7/1/2020 6/30/2021 Instruction at Binghamton University the Humanities Valerie Imbruce Beckman Scholars Program 2021 Arnold and Mabel 100% $573,000 6/1/2021 5/31/2024 Beckman Foundation Total # Credited 2.20 Total $ Credited $969,593 020 Academic Affairs/Library Services Amy Gay COVID: Center for the Study of the 1960s: Institute of Museum and 100% $328,792 9/1/2020 8/31/2022 McKiernan Oral Interview Collection Library Services Heather Parks 2019-2020 Conservation & Preservation NYS Education Department 100% $61,955 4/1/2019 3/31/2020 Program Grant James Galbraith Library Collections 2019 - 2020 NYS Education Department 100% $21,991 7/1/2019 6/30/2020 Total # Credited 3.00 Total $ Credited $412,738 020 Anthropology Carl Lipo Eco-Educators: A Binghamton University- Environmental Protection 10% $10,000 1/1/2021 12/31/2021 Community Partnership for a Healthier Agency Chesapeake Bay Watershed Elizabeth Digangi Doctoral Dissertation Research: Support for National Science 100% $25,331 9/1/2020 8/31/2021 Helen Brandt: A Virtual Anthropological Foundation Approach to the Study of Commingled Human Remains
    [Show full text]
  • MARTIN HOLT Phone: 630-252-5180 Scientist, Nanoscience Fax: 630-252-0439 E-Mail: [email protected]
    Center for Nanoscale Materials Building 440, Room A139 MARTIN HOLT Phone: 630-252-5180 Scientist, Nanoscience Fax: 630-252-0439 E-mail: [email protected] Electron and X-ray Microscopy Group Argonne National Laboratory 9700 S Cass Ave., Argonne, IL 60439 Education Ph. D. Physics, University of Illinois Urbana-Champaign (2002) B. A. Physics and Mathematics, Rice University (1998) Research • Predictive control of classical and quantum material response at the nanoscale through interests synchrotron microscopy of strain, scaling, and structural dynamics • Coherent x-ray diffraction imaging and Bragg ptychography for nanoscale structural studies Argonne National Laboratory - Center for Nanoscale Materials (CNM) 2010-present Professional Scientist, Nanoscience Experience • Beamline Director - CNM/APS Hard X-ray Nanoprobe Beamline (2016 – present) Scientific productivity increase of ~2x over this time period o o APS-U Beamline Enhancement awarded - “The 4D Nanoprobe” • Scientific lead - CNM X-ray diffraction microscopy program (2010 – present) o Demonstrated 3D Bragg Projection Ptychography at ~20nm^3 resolution o Demonstrated 2D Bragg Projection Ptychography at 5nm spatial resolution o Observed large wave-vector phonon confinement in 10nm semiconductor membranes Argonne National Laboratory – Center for Nanoscale Materials (CNM) 2004-2010 Assistant Physicist • Co-principal investigator of Hard X-ray Nanoprobe Beamline Project – design, construction, commissioning, and acceptance • Development of a non-goniometer-based approach to hard x-ray nanoscale
    [Show full text]
  • Chip Scale Atomic Clock for Space  Space Qualified Crystal Oscillators  Oscillator Subsystems & Atomic Clocks for Space  Summary
    Space Timing Products Peter Cash Space Forum 2019 Agenda Space Qualified Oscillators & Clocks Frequency & Timing Division New Product: Chip Scale Atomic Clock for Space Space Qualified Crystal Oscillators Oscillator subsystems & atomic clocks for space Summary Space Forum 2019 2 Complete Timing (I) ID Market Position & ProductsT #1 supplier of IEEE1588, SyncE & GNSS network synchronization PLL IC and software Timing since 1992 Supplier of low phase noise/jitter PLL IC Clock synthesis, rate conversion, jitter attenuation and fan-out buffers Oscillators (TCXO), Timers Oscillators (MEMS, Normal), Clock Generators (Normal, PCIe) Oscillator Die, Clock Generators (Normal, PCIe, VCXO), Clock Conditioning, Buffers (Zero Delay) Clock Synthesizers, Buffers (PCIe), Multiplexers & Cross Point Switches, Logic Translators, Skew Management Timing since 1938 XO, VCXO, VCSO TCXO, OCXO - SAW & BAW technology GPS Disciplined Oscillators Precision Crystal (OCXO, TCXO) Embedded Atomic Clocks (CSAC, MAC) GPS Disciplined Oscillators Leader in high-precision IEEE1588 timestamping and SyncE PHY IC. Full support for precise MACSec Integrated Time Synchronization Module for IEEE1588 and SyncE SmartFusion2 SoC/FPGA IC complete software solution & reference design Space Forum 2019 3 Complete Timing (II) Rubidium Hydrogen Maser Cesium Rubidium CSAC OCXO EMXO TCXO VCXO/XO MEMS CPT Model Number MHM 2010 5071A XPRO SA.35 SA.45s OX-208 EX-421 TX-503 VT-803 MXT57 VC-840 DSC6100 Dimensions (cc) 500E+3 20E+3 338.4 45 17 13.3 1.521 506E-3 23E-3 15E-3 4E-3 2E-3 Temperature
    [Show full text]
  • Quantum Coherence Thermal Transistors
    Quantum coherence thermal transistors Shanhe Su,1 Yanchao Zhang,1 Bjarne Andresen,2 Jincan Chen1∗ 1Department of Physics and Jiujiang Research Institute, Xiamen University, Xiamen 361005, China. 2Niels Bohr Institute, University of Copenhagen, Universitetsparken 5, DK-2100 Copenhagen Ø, Denmark. (Dated: May 31, 2021) Coherent control of self-contained quantum systems offers the possibility to fabricate smallest thermal transistors. The steady coherence created by the delocalization of electronic excited states arouses nonlinear heat transports in non-equilibrium environment. Applying this result to a three- level quantum system, we show that quantum coherence gives rise to negative differential thermal resistances, making the thermal transistor suitable for thermal amplification. The results show that quantum coherence facilitates efficient thermal signal processing and can open a new field in the application of quantum thermal management devices. PACS numbers: 05.90. +m, 05.70. –a, 03.65.–w, 51.30. +i A thermal transistor, like its electronic counterpart, is thermal flux is normally higher than the controlling (in- capable of implementing heat flux switching and mod- put) thermal flux, a thermal transistor is able to amplify ulating. The effects of negative differential thermal re- or switch a small signal. The amplification factor must sistance (NDTR) play a key role in the development of be tailored to suit specific situations. The Scovil and thermal transistors [1]. Classical dynamic descriptions Schulz-DuBois maser model is not applicable for fabricat- utilizing Frenkel-Kontorova lattices conclude that nonlin- ing thermal transistors, owing to the fact that its ampli- ear lattices are the origin of NDTR [2, 3]. Ben-Abdallah fication factor is simply a constant defined by the maser et al.
    [Show full text]
  • (1)4» W Transmission US 7,711,015 B2 Page 2
    US007711015B2 (12) Unlted States Patent (10) Patent N0.2 US 7,711,015 B2 Holonyak, Jr. et al. (45) Date of Patent: May 4, 2010 (54) METHOD FOR CONTROLLING OPERATION 4,845,535 A 7/1989 Yamanishi et a1. ........ .. 315/172 OF LIGHT EMITTING TRANSISTORS AND 4,958,208 A 9/1990 Tanaka ........... .. 357/34 LASER TRANSISTORS 5,003,366 A 3/1991 Mishima et al. 357/34 5,239,550 A 8/1993 Jain .......................... .. 372/45 75 _ . _ 5,293,050 A 3/1994 Chapple-Sokolet al. .... .. 257/17 ( ) Inventors‘ H‘irlonyagilh" UrbanIaL’ IL gs)’ 5,334,854 A 8/1994 Ono et al. ................... .. 257/13 1 0,“ eng’ ampalgn’ (U )’ 5,389,804 A 2/1995 Yokoyama et al. 257/197 Gabnelwalter, Urbana> IL (Us) 5,399,880 A 3/1995 Chand ............ .. 257/21 _ 5,414,273 A 5/1995 Shimura et al. ....... .. 257/17 (73) Asslgneei Th1? Board 0fTr_l1st_ees of The 5,588,015 A 12/1996 Yang .............. .. .. 372/45012 Unlverslty 0f 111111018, Urbana, IL (US) 5,684,308 A 11/1997 Lovejoy etal. ........... .. 257/184 5,723,872 A 3/1998 Seabaugh et al. ........... .. 257/25 ( * ) Notice: Subject to any disclaimer, the term of this patent is extended or adjusted under 35 (Continued) USC‘ 1540’) by 240 days‘ FOREIGN PATENT DOCUMENTS (21) APP1- NO-I 11/805359 JP 61231788 10/1986 (22) Filed: May 24, 2007 (Continued) (65) Prior Publication Data OTHER PUBLICATIONS Us Zoos/0240173 A1 Oct 2’ 2008 Light-Emitting Transistor: Light Emission From InGaP/GaAs Heterojunction Bipolar Transistors, M. Feng, N.
    [Show full text]
  • Cyclotron Autoresonance Maser (CARM) Amplifiers for RF Accelerator Drivers
    © 1991 IEEE. Personal use of this material is permitted. However, permission to reprint/republish this material for advertising or promotional purposes or for creating new collective works for resale or redistribution to servers or lists, or to reuse any copyrighted component of this work in other works must be obtained from the IEEE. Cyclotron Autoresonance Maser (CARM) Amplifiers for RF Accelerator Drivers W.L. Menningcr, B.G. Danly, C. Chen, K.D. Pendergast,and R.J. Temkin Plasma Fusion Center MassachusettsInstitute of Technology Cambridge, Massachusetts02139 D.L. Goodman, D.L. Birx Scientific ResearchLaboratory Sommerville. Massachusetts Abstract C. Description of a CARM Cyclotron autoresonancemaser (CARM) ampliiiers are un- The CARM is similar to a gyrotron, except that the elec- der investigation as a possible source of high-power (>lOO tromagnetic wave propagates with a phase velocity close to MW), high-frequency (>lO GHz) microwaves for powering the speed of light. The CARM typically employs relativistic the next generation of linear colliders. A design for a high- electron beams with pitch angles (a = ~~1/~1) smaller than power, short pulse, 17.136 GHz CARM amplifier, utilizing a that of the gyrotron. However, unlike gyrotrons and frce- 500 kV linear induction accelerator, is prcsentcd. electron lasers, there are few experimental demonstrations of the CARM [8,9,101. I. INTRODUCTION In design of a high-peak power CARM amplifier, the elec- tron beam energieswhich result in the most attractive operation are typically in the 0.5 - 2 MeV range. Consequently, beam A. Next Generation Collider Requirements generation for a high-power CARM amplifier is well suited to two accelerator technologies.
    [Show full text]
  • High Frequency Engineering
    Course Material On High Frequency Engineering Subject Code: PET6I102 Course: - B. Tech Discipline: - Electronics and Telecommunication Engineering Semester: - 6th Syllabus HIGH FREQUENCY ENGINEERING (PET6I102) MODULE-I Microwave Tubes- Limitations of conventional tubes, construction, operation; Properties of Klystron Amplifier, reflex Klystron, Magnetron, Travelling Wave Tube (TWT); Backward Wave Oscillator (BWO); Crossed field amplifiers. MODULE-II Microwave Solid State Devices- Limitation of conventional solid state devices at Microwaves; Transistors (Bipolar, FET); Diodes (Tunnel, Varactor, PIN), Transferred Electron Devices (Gunn diode); Avalanche transit time effect (IMPATT, TRAPATT, SBD); Microwave Amplification by Stimulated Emission of Radiation (MASER). MODULE-III Microwave Components- Analysis of Microwave components using s-parameters, Junctions (E, H, Hybrid), Directional coupler; Bends and Corners; Microwave posts, S.S. tuners, Attenuators, Phase shifter, Ferrite devices (Isolator, Circulator, Gyrator); Cavity resonator. MODULE-IV Introduction to Radar Systems- Basic Principle-Block diagram and operation of Radar; Radar range Equation; Pulse Repetition Frequency (PRF) and Range Ambiguities. Doppler Radars- Doppler determination of velocity, Continuous Wave (CW) radar and its limitations, Frequency Modulated Continuous Wave (FMCW) radar, Basic principle and operation of Moving Target Indicator (MTI) radar, Delay line cancellers, Blind speeds and staggered PRFs. Scanning and Tracking Techniques- Various scanning techniques (Horizontal, vertical, spiral, palmer, raster, nodding); Angle tracking systems (Lobe switching, conical scan, mono pulse). COPYRIGHT IS NOT RESERVED BY AUTHORS. AUTHOR IS NOT RESPONSIBLE FOR ANY LEGAL ISSUES ARISING OUT OF ANY COPYRIGHT DEMANDS AND/OR REPRINT ISSUES CONTAINED IN THIS MATERIALS. THIS IS NOT MEANT FOR ANY COMMERCIAL PURPOSE & ONLY MEANT FOR PERSONAL USE OF STUDENTS FOLLOWING SYLLABUS PRINTED IN PREVIOUS PAGE.
    [Show full text]
  • MASER FREQUENCY STABILITY Richard C
    MASER FREQUENCY STABILITY Richard C. Mockler and James A. Barnes National Bureau of Standards Boulder Laboratories The frequency stability of an ammonia maser is ordinarily quite high for periods of a few minutes. However, to preserve this stability for long periods of time - hours and days - requires rather careful control of the parameters of the system which affect the frequency - in particular the pres- sure, focuser voltage and cavity temperature. We have had some success with the se problems. Method and Results of Long Term Stabilitv Tests In order to facilitate frequency comparison and also to gain the greatest possible use of the high stability of the maser, it has proved useful to use the maser as a stabilizing device for a frequency multiplier chain. We then expect that at any point along the chain we may take signals at useful power levels, and these signals will have stabilities closely approaching that of the maser itself. A block diagram of the maser stabilized chain is shown in figure 1 together with auxiliary apparatus for the purpose of comparing a 5 MC helium cooled crystal oscillator with the stabilized chain. The servo time constant is about 0. 1 millisecond. Figure 2 shows a comparison of a helium cooled oscillator with the maser stabilized chain; the maximum drift in relative frequency over a two hour period was about 2 X 10-l l. In these experiments the maser cavity temperature was controlled to within . OOl°C with two pro- portionally controlled thermostats - one inside the other. Figure 3 shows some of the best frequency comparisons that we have succeeded in making between two masers.
    [Show full text]
  • CRYOGENIC HYDROGEN MASER by . Martin Dominik Hiirlimann Dipl
    CRYOGENIC HYDROGEN MASER By . Martin Dominik Hiirlimann Dipl. Natw. ETH, Swiss Federal Institute of Technology, Zurich A THESIS SUBMITTED IN PARTIAL FULFILLMENT OF THE REQUIREMENTS FOR THE DEGREE OF DOCTOR OF PHILOSOPHY in THE FACULTY OF GRADUATE STUDIES PHYSICS We accept this thesis as conforming to the required standard THE UNIVERSITY OF BRITISH COLUMBIA July 1989 © Martin Dominik Hiirlimann, 1989 In presenting this thesis in partial fulfilment of the requirements for an advanced degree at the University of British Columbia, I agree that the Library shall make it freely available for reference and study. I further agree that permission for extensive copying of this thesis for scholarly purposes may be granted by the head of my department or by his or her representatives. It is understood that copying or publication of this thesis for financial gain shall not be allowed without my written permission. Department The University of British Columbia Vancouver, Canada DE-6 (2/88) Abstract A new type of atomic hydrogen maser that operates in a dilution refrigerator has been developed. In this device, the hydrogen atoms circulate back and forth between a mi• crowave pumped state invertor in high field and the maser cavity in zero field. A prototype maser with a small maser cavity has been built and the results obtained so far are encouraging. Stable maser oscillations were observed for temperatures of the maser bulb between 230 mK and 660 mK and for densities up to 3 x 1012cm-3. The short term frequency stability was measured with the help of two high quality quartz crystal oscillators by the three-cornered-hat method.
    [Show full text]