MASER FREQUENCY STABILITY Richard C
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Crystal Oscillators 1
Crystal oscillators 1. Objectives The aim of the exercise is to get acquainted with issues concerning the generation of waveforms (including sinewaves) in the basic structures of crystal generators. In addition, the exercise aims to familiarize with surface mount technique SMT (Surface Mount Technology/ Technics or SMD – Surface mounting Devices). 2. Components and instrumentation. In the exercise, it is possible to test quartz generators operating in the three simplest and most popular system structures: • Colpitts-Pierce quartz generator with bipolar transistor, • quartz generator implemented on TTL gates, • quartz generator implemented on CMOS inverters 2.1. Colpittsa-Pierce’s oscillator with bipolar transistor. The Colpitts-Pierce quartz generator system working in parallel resonance is shown in Fig. 1. + UCC Rb C2 XT C1 Re UWY Fig. 1. Colpittsa-Pierce oscillator with BJT. Using, in the system, quartz resonators with resonance values up to several tens of MHz, the elements C1, Re in the generator system can be selected according to the graph shown in Fig.2. RezystorRe [Ohm] Frequency [MHz] Fig. 2. Selection of C1 and Re elements in the Colpitts-Pierce oscillator 2.2. Quartz oscillator implemented using TTL digital IC Fig. 3 presents a diagram of a quartz oscillator implemented using NAND gates in TTL technology. The oscillator works in series resonance. In this system, while maintaining the same resistance values, quartz resonators with a frequency from a few to 10 MHz can be used. 560 1k8 220 220 UWY XT Fig. 3. Cristal oscillator with serial resonance implemented with NAND gates in TTL technology In the laboratory exercise, it is proposed to implement the system using TTL series 74LS00 (pins of the IC are shown in in Fig.4). -

Analysis of BJT Colpitts Oscillators - Empirical and Mathematical Methods for Predicting Behavior Nicholas Jon Stave Marquette University
Marquette University e-Publications@Marquette Master's Theses (2009 -) Dissertations, Theses, and Professional Projects Analysis of BJT Colpitts Oscillators - Empirical and Mathematical Methods for Predicting Behavior Nicholas Jon Stave Marquette University Recommended Citation Stave, Nicholas Jon, "Analysis of BJT Colpitts sO cillators - Empirical and Mathematical Methods for Predicting Behavior" (2019). Master's Theses (2009 -). 554. https://epublications.marquette.edu/theses_open/554 ANALYSIS OF BJT COLPITTS OSCILLATORS – EMPIRICAL AND MATHEMATICAL METHODS FOR PREDICTING BEHAVIOR by Nicholas J. Stave, B.Sc. A Thesis submitted to the Faculty of the Graduate School, Marquette University, in Partial Fulfillment of the Requirements for the Degree of Master of Science Milwaukee, Wisconsin August 2019 ABSTRACT ANALYSIS OF BJT COLPITTS OSCILLATORS – EMPIRICAL AND MATHEMATICAL METHODS FOR PREDICTING BEHAVIOR Nicholas J. Stave, B.Sc. Marquette University, 2019 Oscillator circuits perform two fundamental roles in wireless communication – the local oscillator for frequency shifting and the voltage-controlled oscillator for modulation and detection. The Colpitts oscillator is a common topology used for these applications. Because the oscillator must function as a component of a larger system, the ability to predict and control its output characteristics is necessary. Textbooks treating the circuit often omit analysis of output voltage amplitude and output resistance and the literature on the topic often focuses on gigahertz-frequency chip-based applications. Without extensive component and parasitics information, it is often difficult to make simulation software predictions agree with experimental oscillator results. The oscillator studied in this thesis is the bipolar junction Colpitts oscillator in the common-base configuration and the analysis is primarily experimental. The characteristics considered are output voltage amplitude, output resistance, and sinusoidal purity of the waveform. -

GALLIUM OXIDE METAL OXIDE SEMICONDUCTOR FIELD EFFECT TRANSISTOR ANALYTICAL MODELING and POWER TRANSISTOR DESIGN TRADES By
GALLIUM OXIDE METAL OXIDE SEMICONDUCTOR FIELD EFFECT TRANSISTOR ANALYTICAL MODELING AND POWER TRANSISTOR DESIGN TRADES by Neil Austin Moser A Dissertation Submitted to the Graduate Faculty of George Mason University in Partial Fulfillment of The Requirements for the Degree of Doctor of Philosophy Electrical and Computer Engineering Committee: _________________________________ Dr. Nathalia Peixoto, Dissertation Director _________________________________ Dr. Qiliang Li, Committee Member _________________________________ Dr. Yuri Mishin, Committee Member _________________________________ Dr. Gregg Jessen, Committee Member _________________________________ Dr. Monson Hayes, Department Chair _________________________________ Dr. Kenneth S. Ball, Dean, Volgenau School of Engineering Date:_____________________________ Fall Semester 2017 George Mason University Fairfax, VA Gallium Oxide Metal Oxide Semiconductor Field Effect Transistor Analytical Modeling and Power Transistor Design Trades A Dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy at George Mason University by Neil Austin Moser Master of Science George Mason University, 2013 Bachelor of Science University of Michigan-Ann Arbor, 2002 Director: Nathalia Peixoto, Professor Department of Electrical and Computer Engineering Fall Semester 2017 George Mason University Fairfax, VA Copyright 2017 Neil Austin Moser All Rights Reserved ii DEDICATION This is dedicated to my father, Gary Moser, who started me on the path to being an academic before I even really knew what that was and still encourages me to not be ignorant about anything to this day. iii ACKNOWLEDGEMENTS I would like to thank my wife, Morgan, and daughter, Schaefer, for putting up with me “working” on this for quite a long time. Also, I would like to thank my committee, especially Gregg Jessen who helped me find this exciting research and shepherded me the whole way and Nathalia Peixoto who put up with a lot of dead ends and redirections in topic along the way. -

A Nanoscale Study of Mosfets Reliability and Resistive Switching in RRAM Devices
ADVERTIMENT. Lʼaccés als continguts dʼaquesta tesi queda condicionat a lʼacceptació de les condicions dʼús establertes per la següent llicència Creative Commons: http://cat.creativecommons.org/?page_id=184 ADVERTENCIA. El acceso a los contenidos de esta tesis queda condicionado a la aceptación de las condiciones de uso establecidas por la siguiente licencia Creative Commons: http://es.creativecommons.org/blog/licencias/ WARNING. The access to the contents of this doctoral thesis it is limited to the acceptance of the use conditions set by the following Creative Commons license: https://creativecommons.org/licenses/?lang=en Universitat Autònoma de Barcelona Escola d’Enginyeria Electronic Engineering Department A nanoscale study of MOSFETs reliability and Resistive Switching in RRAM devices A dissertation submitted by Qian Wu in fulfillment of the requirements for the Degree of Doctor of Philosophy in Electronic and Telecommunication Engineering Supervised by Dr. Marc Porti i Pujal Bellaterra, November 2016 Universitat Autònoma de Barcelona Escola d’Enginyeria Electronic Engineering Department Dr. Marc Porti i Pujal, associate professor of the Electronic Engineering Department of the Universitat Autònoma de Barcelona, Certifies That the dissertation: A nanoscale study of MOSFETs reliability and Resistive Switching in RRAM devices submitted by Qian Wu to the School of Engineering in fulfillment of the requirements for the Degree of Doctor in the Electronic and Telecommunication Engineering Program, has been performed under his supervision. Dr. Marc Porti Bellaterra, November of 2016 To my family Acknowledgement The four years’ doctoral study is a significant and unforgettable experience for me. Many kind-hearted people give me a great amount of help, professional advice and encouragement. -

Custom Design of Monolithic Microwave Integrated Circuits
CRAIG R. MOORE and JOHN E. PENN CUSTOM DESIGN OF MONOLITHIC MICROWAVE INTEGRATED CIRCUITS Monolithic microwave integrated circuits (MMIC'S) have been designed at the Applied Physics Laboratory and fabricated at several gallium arsenide foundries since 1989. The design tools and methods for designing MMIC'S have evolved to the present use of integrated computer-aided engineering software with programmable design components. Software elements that can be customized create multilayer mask descriptions of components for transistors, resistors, capacitors, inductors, microstrip connections, and other structures to improve the quality and productivity of MMIC's designed at the Laboratory. The schematic, physical layout, and simulation models are integrated into a single software tool, eliminating much potential for error. Experience with various foundries and various MMIC design techniques have increased our ability to design at higher and higher frequencies with confidence in achieving first-time success. The design improvements have been accompanied by improvements in measurement techniques for higher frequencies using microwave probe stations. This article summarizes MMIC designs at the Laboratory over the past few years and the progress shown and lessons learned. COMPUTER-AIDED ENGINEERING DESIGN OF MMIC'S Software computer-aided engineering tools from and custom electrical models. Today, EEsof has a new EEsof, Inc., are the predominant means of designing TriQuint Smart Library containing physical and electrical monolithic microwave integrated circuits (MMIC'S) at APL. macros, which is being used in the MMIC design course A key feature of EEsof's Academy software for MMIC at JHU taught by both authors of this article. layout is the ease of adding both layout macros and A group of people including Dale Dawson of Westing custom electrical models. -
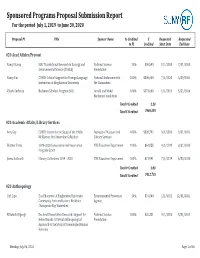
Sponsored Programs Proposal Submission Report for the Period July 1, 2019 to June 30, 2020
Sponsored Programs Proposal Submission Report For the period July 1, 2019 to June 30, 2020 Proposal PI Title Sponsor Name % Credited $ Requested Requested to PI Credited Start Date End Date 020 Acad Affairs/Provost Nancy Stamp IGE: Translational Research in Ecology and National Science 20% $96,593 8/1/2020 7/31/2023 Environmental Science (TREES) Foundation Nancy Um COVID: Critical Support for Foreign Language National Endowment for 100% $300,000 7/1/2020 6/30/2021 Instruction at Binghamton University the Humanities Valerie Imbruce Beckman Scholars Program 2021 Arnold and Mabel 100% $573,000 6/1/2021 5/31/2024 Beckman Foundation Total # Credited 2.20 Total $ Credited $969,593 020 Academic Affairs/Library Services Amy Gay COVID: Center for the Study of the 1960s: Institute of Museum and 100% $328,792 9/1/2020 8/31/2022 McKiernan Oral Interview Collection Library Services Heather Parks 2019-2020 Conservation & Preservation NYS Education Department 100% $61,955 4/1/2019 3/31/2020 Program Grant James Galbraith Library Collections 2019 - 2020 NYS Education Department 100% $21,991 7/1/2019 6/30/2020 Total # Credited 3.00 Total $ Credited $412,738 020 Anthropology Carl Lipo Eco-Educators: A Binghamton University- Environmental Protection 10% $10,000 1/1/2021 12/31/2021 Community Partnership for a Healthier Agency Chesapeake Bay Watershed Elizabeth Digangi Doctoral Dissertation Research: Support for National Science 100% $25,331 9/1/2020 8/31/2021 Helen Brandt: A Virtual Anthropological Foundation Approach to the Study of Commingled Human Remains -

AN826 Crystal Oscillator Basics and Crystal Selection for Rfpic™ And
AN826 Crystal Oscillator Basics and Crystal Selection for rfPICTM and PICmicro® Devices • What temperature stability is needed? Author: Steven Bible Microchip Technology Inc. • What temperature range will be required? • Which enclosure (holder) do you desire? INTRODUCTION • What load capacitance (CL) do you require? • What shunt capacitance (C ) do you require? Oscillators are an important component of radio fre- 0 quency (RF) and digital devices. Today, product design • Is pullability required? engineers often do not find themselves designing oscil- • What motional capacitance (C1) do you require? lators because the oscillator circuitry is provided on the • What Equivalent Series Resistance (ESR) is device. However, the circuitry is not complete. Selec- required? tion of the crystal and external capacitors have been • What drive level is required? left to the product design engineer. If the incorrect crys- To the uninitiated, these are overwhelming questions. tal and external capacitors are selected, it can lead to a What effect do these specifications have on the opera- product that does not operate properly, fails prema- tion of the oscillator? What do they mean? It becomes turely, or will not operate over the intended temperature apparent to the product design engineer that the only range. For product success it is important that the way to answer these questions is to understand how an designer understand how an oscillator operates in oscillator works. order to select the correct crystal. This Application Note will not make you into an oscilla- Selection of a crystal appears deceivingly simple. Take tor designer. It will only explain the operation of an for example the case of a microcontroller. -

MARTIN HOLT Phone: 630-252-5180 Scientist, Nanoscience Fax: 630-252-0439 E-Mail: [email protected]
Center for Nanoscale Materials Building 440, Room A139 MARTIN HOLT Phone: 630-252-5180 Scientist, Nanoscience Fax: 630-252-0439 E-mail: [email protected] Electron and X-ray Microscopy Group Argonne National Laboratory 9700 S Cass Ave., Argonne, IL 60439 Education Ph. D. Physics, University of Illinois Urbana-Champaign (2002) B. A. Physics and Mathematics, Rice University (1998) Research • Predictive control of classical and quantum material response at the nanoscale through interests synchrotron microscopy of strain, scaling, and structural dynamics • Coherent x-ray diffraction imaging and Bragg ptychography for nanoscale structural studies Argonne National Laboratory - Center for Nanoscale Materials (CNM) 2010-present Professional Scientist, Nanoscience Experience • Beamline Director - CNM/APS Hard X-ray Nanoprobe Beamline (2016 – present) Scientific productivity increase of ~2x over this time period o o APS-U Beamline Enhancement awarded - “The 4D Nanoprobe” • Scientific lead - CNM X-ray diffraction microscopy program (2010 – present) o Demonstrated 3D Bragg Projection Ptychography at ~20nm^3 resolution o Demonstrated 2D Bragg Projection Ptychography at 5nm spatial resolution o Observed large wave-vector phonon confinement in 10nm semiconductor membranes Argonne National Laboratory – Center for Nanoscale Materials (CNM) 2004-2010 Assistant Physicist • Co-principal investigator of Hard X-ray Nanoprobe Beamline Project – design, construction, commissioning, and acceptance • Development of a non-goniometer-based approach to hard x-ray nanoscale -

Crystals Load Capacitance Calculation And
Load Capacitance PRINTED: 12/21/2012 TYPICAL OSCILLATOR CIRCUIT OSC CELL OSC CELL = oscillator circuit integrated into any IC. Rf = feedback resistor, sometimes integrated in IC or is required as external resistor Rf CLOCK SIGNAL Cg = capacitance of oscillator input for IC internal use Cd = capacitance of oscillator output Rd = Phase shift resistor, necessary at lower frequencies to meet oscillation condition that phase shift all the way around the oscillator loop need to add up to 360°. Y1 = Quartz crystal unit C1 and C1 = external load capacitors. CPCB1 and CPCB2 = stray capacitances of PCB traces Cg Cd The total LOAD CAPACITANCE of the oscillator circuit is the sum of all capacitances. OSC IN OSC OUT consisting of: 1. The two external capacitors (here called C1 and C2) 2. The IC input and output capacitances (here called Cg and Cd) 3. The stray capacitances of PCB traces (here called CPCB1 and CPCB2) CPCB1 Rd Commonly being only the values of the external capacitors known so that a correct calculation of the actual load capacitance is not possible. SIGNAL OUTPUT OPTIONALCLOCK In such case we use simlified formula to calculate the load capacitance as: C1 C2 CL C TOTAL C1 C2 STRAY CPCB2 Here C1 and C2 are the external capacitors in the cricuit, values should be known. Cstray is summarized value for IC input and output capacitance and the PCB traces. Y1 Cstray in a 3.3VDC circuit is often 3~4pF. C1 C2 Cstray in a 5.0VDC circuit often 5~7pF. However, we have also seen circuits that had large deviation from these values. -

Chip Scale Atomic Clock for Space Space Qualified Crystal Oscillators Oscillator Subsystems & Atomic Clocks for Space Summary
Space Timing Products Peter Cash Space Forum 2019 Agenda Space Qualified Oscillators & Clocks Frequency & Timing Division New Product: Chip Scale Atomic Clock for Space Space Qualified Crystal Oscillators Oscillator subsystems & atomic clocks for space Summary Space Forum 2019 2 Complete Timing (I) ID Market Position & ProductsT #1 supplier of IEEE1588, SyncE & GNSS network synchronization PLL IC and software Timing since 1992 Supplier of low phase noise/jitter PLL IC Clock synthesis, rate conversion, jitter attenuation and fan-out buffers Oscillators (TCXO), Timers Oscillators (MEMS, Normal), Clock Generators (Normal, PCIe) Oscillator Die, Clock Generators (Normal, PCIe, VCXO), Clock Conditioning, Buffers (Zero Delay) Clock Synthesizers, Buffers (PCIe), Multiplexers & Cross Point Switches, Logic Translators, Skew Management Timing since 1938 XO, VCXO, VCSO TCXO, OCXO - SAW & BAW technology GPS Disciplined Oscillators Precision Crystal (OCXO, TCXO) Embedded Atomic Clocks (CSAC, MAC) GPS Disciplined Oscillators Leader in high-precision IEEE1588 timestamping and SyncE PHY IC. Full support for precise MACSec Integrated Time Synchronization Module for IEEE1588 and SyncE SmartFusion2 SoC/FPGA IC complete software solution & reference design Space Forum 2019 3 Complete Timing (II) Rubidium Hydrogen Maser Cesium Rubidium CSAC OCXO EMXO TCXO VCXO/XO MEMS CPT Model Number MHM 2010 5071A XPRO SA.35 SA.45s OX-208 EX-421 TX-503 VT-803 MXT57 VC-840 DSC6100 Dimensions (cc) 500E+3 20E+3 338.4 45 17 13.3 1.521 506E-3 23E-3 15E-3 4E-3 2E-3 Temperature -

MEMS) Technology
Microchip Oscillators and Clocks Using Microelectromechanical Systems (MEMS) Technology Author: John Clark and Graham Mostyn The next milestone will be next-generation MEMS res- Microchip Technology Inc. onators that achieve very low phase noise for high-end communication systems. Microchip acquired MEMS timing technology through OVERVIEW the purchases of Discera and Micrel in 2015. Since Dis- For decades, oscillators and clocks have relied on cera shipped its first production oscillators in 2008, quartz crystals for the creation of a stable frequency almost 100 million devices have been manufactured reference. Crystals perform very well for many applica- and sold. tions. However, microelectromechanical systems This paper describes the benefits of a MEMS-based (MEMS) technology, replacing quartz crystals with solution, the resonator technology, and the design of MEMS resonators, entered the marketplace ten years the final product. ago and is rapidly maturing. MEMS-based timing devices offer high reliability KEY FUNCTIONALITY (including AEC-Q100 certification for automotive use), extended operating temperatures, small size, and low Microchip’s MEMS-based oscillators and clocks offer power consumption. Video surveillance, automotive benefits over traditional quartz solutions (Figure 1). ADAS, general industrial applications, and data trans- These include stable frequency, small size, high reli- mission to 10 Gbps are prime areas of usage today. ability, flexibility, many programmable features, fast guaranteed start-up, and high integration. FIGURE 1: Benefits of Microchip MEMS-Based Oscillators and Clocks. 2017 Microchip Technology Inc. DS00002344A-page 1 MICROCHIP RESONATOR quency of the beam and minimize vibrational energy TECHNOLOGY loss to the substrate. This, in turn, maximizes its quality factor and frequency selectivity. -

Microcontroller Oscillator Circuit Design Considerations by Cathy Cox and Clay Merritt
Freescale Semiconduct or, Inc... 2 CrystalOscillatorTheory 1 Introduction By CathyCoxandClayMerritt Considerations Microcontroller OscillatorCircuitDesign can beexpected,asignificantamountofpowerisrequiredtokeepanamplifierinlinearmode. digital NANDgateasananalogamplifierisnotlogical,butthishowoscillatorcircuitfunctions.As The voltageincreasesuntiltheNANDgateamplifiersaturates.Atfirstglance,thoughtofusinga energized, theloopgainmustbegreaterthanonewhilevoltageatXTALgrowsovermultiplecycles. overall loopgainequaltooneandanphaseshiftthatisintegermultipleof360 stabilize thefrequencyandsupply180 sists oftwoparts:aninvertingamplifierthatsuppliesavoltagegainand180 The Pierce-typeoscillatorcircuitshownin pitfalls. document istodevelopasystematicapproachgoodoscillatordesignandpointoutsomecommon ing crystalandmicrocontrollerfunctionswithoutthehelpofmatingspecifications.Theobjectivethis timing overawidetemperaturerangeusecrystaloscillator.PCBdesignershavethetaskofintegrat- The heartbeatofeverymicrocontrollerdesignistheoscillatorcircuit.Mostdesignsthatdemandprecise cy selectivefeedbackpath.ThecrystalcombinedwithC 1. 2.The M68HC11oscillatorcircuitpinsarelabeledXTALand EXTAL. forpowerconservation. STOP isaninternallygeneratedsignalthatdisablestheoscillator circuit EXTAL Cx STOP Figure 1PierceOscillator 2 ° phaseshiftfeedbackpath.Insteadystate,thiscircuithasan 1 Figure 1 Rf Y1 isusedonmostmicrocontrollers.Thiscircuitcon- x andC y formatunedPInetworkthattendsto XTAL Cy 2 ° phaseshiftandafrequen- Order thisdocument byAN1706/D ° . Uponbeing Freescale Semiconductor,