Tracerx: Dynamic Symbolic Execution with Interpolation
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Process Text Streams Using Filters
Process Text Streams Using Filters OBJECTIVE: Candidates should should be able to apply filters to text streams. 1 Process Text Streams Using Filters KeyKEY knowledge KNOWLEDGE area(s): AREAS: Send text files and output streams through text utility filters to modify the output using standard UNIX commands found in the GNU textutils package. 2 Process Text Streams Using Filters KEY FILES,TERMS, UTILITIES cat nl tail cut paste tr expand pr unexpand fmt sed uniq head sort wc hexdump split join tac 3 cat cat the editor - used as a rudimentary text editor. cat > short-message we are curious to meet penguins in Prague Crtl+D *Ctrl+D - command is used for ending interactive input. 4 cat cat the reader More commonly used to flush text to stdout. Options: -n number each line of output -b number only non-blank output lines -A show carriage return Example cat /etc/resolv.conf ▶ search mydomain.org nameserver 127.0.0.1 5 tac tac reads back-to-front This command is the same as cat except that the text is read from the last line to the first. tac short-message ▶ penguins in Prague to meet we are curious 6 head or tail using head or tail - often used to analyze logfiles. - by default, output 10 lines of text. List 20 first lines of /var/log/messages: head -n 20 /var/log/messages head -20 /var/log/messages List 20 last lines of /etc/aliases: tail -20 /etc/aliases 7 head or tail The tail utility has an added option that allows one to list the end of a text starting at a given line. -

The Linux Command Line
The Linux Command Line Fifth Internet Edition William Shotts A LinuxCommand.org Book Copyright ©2008-2019, William E. Shotts, Jr. This work is licensed under the Creative Commons Attribution-Noncommercial-No De- rivative Works 3.0 United States License. To view a copy of this license, visit the link above or send a letter to Creative Commons, PO Box 1866, Mountain View, CA 94042. A version of this book is also available in printed form, published by No Starch Press. Copies may be purchased wherever fine books are sold. No Starch Press also offers elec- tronic formats for popular e-readers. They can be reached at: https://www.nostarch.com. Linux® is the registered trademark of Linus Torvalds. All other trademarks belong to their respective owners. This book is part of the LinuxCommand.org project, a site for Linux education and advo- cacy devoted to helping users of legacy operating systems migrate into the future. You may contact the LinuxCommand.org project at http://linuxcommand.org. Release History Version Date Description 19.01A January 28, 2019 Fifth Internet Edition (Corrected TOC) 19.01 January 17, 2019 Fifth Internet Edition. 17.10 October 19, 2017 Fourth Internet Edition. 16.07 July 28, 2016 Third Internet Edition. 13.07 July 6, 2013 Second Internet Edition. 09.12 December 14, 2009 First Internet Edition. Table of Contents Introduction....................................................................................................xvi Why Use the Command Line?......................................................................................xvi -

IBM Education Assistance for Z/OS V2R1
IBM Education Assistance for z/OS V2R1 Item: ASCII Unicode Option Element/Component: UNIX Shells and Utilities (S&U) Material is current as of June 2013 © 2013 IBM Corporation Filename: zOS V2R1 USS S&U ASCII Unicode Option Agenda ■ Trademarks ■ Presentation Objectives ■ Overview ■ Usage & Invocation ■ Migration & Coexistence Considerations ■ Presentation Summary ■ Appendix Page 2 of 19 © 2013 IBM Corporation Filename: zOS V2R1 USS S&U ASCII Unicode Option IBM Presentation Template Full Version Trademarks ■ See url http://www.ibm.com/legal/copytrade.shtml for a list of trademarks. Page 3 of 19 © 2013 IBM Corporation Filename: zOS V2R1 USS S&U ASCII Unicode Option IBM Presentation Template Full Presentation Objectives ■ Introduce the features and benefits of the new z/OS UNIX Shells and Utilities (S&U) support for working with ASCII/Unicode files. Page 4 of 19 © 2013 IBM Corporation Filename: zOS V2R1 USS S&U ASCII Unicode Option IBM Presentation Template Full Version Overview ■ Problem Statement –As a z/OS UNIX Shells & Utilities user, I want the ability to control the text conversion of input files used by the S&U commands. –As a z/OS UNIX Shells & Utilities user, I want the ability to run tagged shell scripts (tcsh scripts and SBCS sh scripts) under different SBCS locales. ■ Solution –Add –W filecodeset=codeset,pgmcodeset=codeset option on several S&U commands to enable text conversion – consistent with support added to vi and ex in V1R13. –Add –B option on several S&U commands to disable automatic text conversion – consistent with other commands that already have this override support. –Add new _TEXT_CONV environment variable to enable or disable text conversion. -
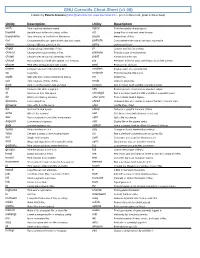
GNU Coreutils Cheat Sheet (V1.00) Created by Peteris Krumins ([email protected], -- Good Coders Code, Great Coders Reuse)
GNU Coreutils Cheat Sheet (v1.00) Created by Peteris Krumins ([email protected], www.catonmat.net -- good coders code, great coders reuse) Utility Description Utility Description arch Print machine hardware name nproc Print the number of processors base64 Base64 encode/decode strings or files od Dump files in octal and other formats basename Strip directory and suffix from file names paste Merge lines of files cat Concatenate files and print on the standard output pathchk Check whether file names are valid or portable chcon Change SELinux context of file pinky Lightweight finger chgrp Change group ownership of files pr Convert text files for printing chmod Change permission modes of files printenv Print all or part of environment chown Change user and group ownership of files printf Format and print data chroot Run command or shell with special root directory ptx Permuted index for GNU, with keywords in their context cksum Print CRC checksum and byte counts pwd Print current directory comm Compare two sorted files line by line readlink Display value of a symbolic link cp Copy files realpath Print the resolved file name csplit Split a file into context-determined pieces rm Delete files cut Remove parts of lines of files rmdir Remove directories date Print or set the system date and time runcon Run command with specified security context dd Convert a file while copying it seq Print sequence of numbers to standard output df Summarize free disk space setuidgid Run a command with the UID and GID of a specified user dir Briefly list directory -

Multiresolution Recurrent Neural Networks: an Application to Dialogue Response Generation
Multiresolution Recurrent Neural Networks: An Application to Dialogue Response Generation Iulian Vlad Serban∗◦ Tim Klinger University of Montreal IBM Research 2920 chemin de la Tour, T. J. Watson Research Center, Montréal, QC, Canada Yorktown Heights, NY, USA Gerald Tesauro Kartik Talamadupula Bowen Zhou IBM Research IBM Research IBM Research T. J. Watson Research Center, T. J. Watson Research Center, T. J. Watson Research Center, Yorktown Heights, Yorktown Heights, Yorktown Heights, NY, USA NY, USA NY, USA Yoshua Bengioy◦ Aaron Courville◦ University of Montreal University of Montreal 2920 chemin de la Tour, 2920 chemin de la Tour, Montréal, QC, Canada Montréal, QC, Canada Abstract We introduce the multiresolution recurrent neural network, which extends the sequence-to-sequence framework to model natural language generation as two parallel discrete stochastic processes: a sequence of high-level coarse tokens, and a sequence of natural language tokens. There are many ways to estimate or learn the high-level coarse tokens, but we argue that a simple extraction procedure is sufficient to capture a wealth of high-level discourse semantics. Such procedure allows training the multiresolution recurrent neural network by maximizing the exact joint log-likelihood over both sequences. In contrast to the standard log- likelihood objective w.r.t. natural language tokens (word perplexity), optimizing the joint log-likelihood biases the model towards modeling high-level abstractions. We apply the proposed model to the task of dialogue response generation in arXiv:1606.00776v2 [cs.CL] 14 Jun 2016 two challenging domains: the Ubuntu technical support domain, and Twitter conversations. On Ubuntu, the model outperforms competing approaches by a substantial margin, achieving state-of-the-art results according to both automatic evaluation metrics and a human evaluation study. -

07 07 Unixintropart2 Lucio Week 3
Unix Basics Command line tools Daniel Lucio Overview • Where to use it? • Command syntax • What are commands? • Where to get help? • Standard streams(stdin, stdout, stderr) • Pipelines (Power of combining commands) • Redirection • More Information Introduction to Unix Where to use it? • Login to a Unix system like ’kraken’ or any other NICS/ UT/XSEDE resource. • Download and boot from a Linux LiveCD either from a CD/DVD or USB drive. • http://www.puppylinux.com/ • http://www.knopper.net/knoppix/index-en.html • http://www.ubuntu.com/ Introduction to Unix Where to use it? • Install Cygwin: a collection of tools which provide a Linux look and feel environment for Windows. • http://cygwin.com/index.html • https://newton.utk.edu/bin/view/Main/Workshop0InstallingCygwin • Online terminal emulator • http://bellard.org/jslinux/ • http://cb.vu/ • http://simpleshell.com/ Introduction to Unix Command syntax $ command [<options>] [<file> | <argument> ...] Example: cp [-R [-H | -L | -P]] [-fi | -n] [-apvX] source_file target_file Introduction to Unix What are commands? • An executable program (date) • A command built into the shell itself (cd) • A shell program/function • An alias Introduction to Unix Bash commands (Linux) alias! crontab! false! if! mknod! ram! strace! unshar! apropos! csplit! fdformat! ifconfig! more! rcp! su! until! apt-get! cut! fdisk! ifdown! mount! read! sudo! uptime! aptitude! date! fg! ifup! mtools! readarray! sum! useradd! aspell! dc! fgrep! import! mtr! readonly! suspend! userdel! awk! dd! file! install! mv! reboot! symlink! -

How Is Dynamic Symbolic Execution Different from Manual Testing? an Experience Report on KLEE
How is Dynamic Symbolic Execution Different from Manual Testing? An Experience Report on KLEE Xiaoyin Wang, Lingming Zhang, Philip Tanofsky University of Texas at San Antonio University of Texas at Dallas Outline ๏ Background ๏ Research Goal ๏ Study Setup ๏ Quantitative Analysis ๏ Qualitative Analysis ๏ Summary and Future Work "2 /27 Background ๏ Dynamic Symbolic Execution (DSE) •A promising approach to automated test generation •Aims to explore all/specific paths in a program •Generates and solves path constraints at runtime ๏ KLEE •A state-of-the-art DSE tool for C programs •Specially tuned for Linux Coreutils •Reported higher coverage than manual testing "3 /27 Research Goal ๏ Understand the ability of state-of-art DSE tools ! ๏ Identify proper scenarios to apply DSE tools ! ๏ Discover potential opportunities for enhancement "4 /27 Research Questions ๏ Are KLEE-based test suites comparable with manually developed test suites on test sufciency? ๏ How do KLEE-based test suites compare with manually test suites on harder testing problems? ๏ How much extra value can KLEE-based test suites provide to manually test suites? ๏ What are the characteristics of the code/mutants covered/killed by one type of test suites, but not by the other? "5 /27 Study Process KLEE tests reduced KLEE tests program manual tests coverage bug finding quality metrics "6 /27 Study Setup: Tools ๏ KLEE •Default setting for ๏ GCOV test generation •Statement coverage •Execute each program collection for 20 minutes ๏ MutGen •Generates 100 mutation faults for each program -

The Linux Command Line
The Linux Command Line Second Internet Edition William E. Shotts, Jr. A LinuxCommand.org Book Copyright ©2008-2013, William E. Shotts, Jr. This work is licensed under the Creative Commons Attribution-Noncommercial-No De- rivative Works 3.0 United States License. To view a copy of this license, visit the link above or send a letter to Creative Commons, 171 Second Street, Suite 300, San Fran- cisco, California, 94105, USA. Linux® is the registered trademark of Linus Torvalds. All other trademarks belong to their respective owners. This book is part of the LinuxCommand.org project, a site for Linux education and advo- cacy devoted to helping users of legacy operating systems migrate into the future. You may contact the LinuxCommand.org project at http://linuxcommand.org. This book is also available in printed form, published by No Starch Press and may be purchased wherever fine books are sold. No Starch Press also offers this book in elec- tronic formats for most popular e-readers: http://nostarch.com/tlcl.htm Release History Version Date Description 13.07 July 6, 2013 Second Internet Edition. 09.12 December 14, 2009 First Internet Edition. 09.11 November 19, 2009 Fourth draft with almost all reviewer feedback incorporated and edited through chapter 37. 09.10 October 3, 2009 Third draft with revised table formatting, partial application of reviewers feedback and edited through chapter 18. 09.08 August 12, 2009 Second draft incorporating the first editing pass. 09.07 July 18, 2009 Completed first draft. Table of Contents Introduction....................................................................................................xvi -

Gnu Coreutils Core GNU Utilities for Version 5.93, 2 November 2005
gnu Coreutils Core GNU utilities for version 5.93, 2 November 2005 David MacKenzie et al. This manual documents version 5.93 of the gnu core utilities, including the standard pro- grams for text and file manipulation. Copyright c 1994, 1995, 1996, 2000, 2001, 2002, 2003, 2004, 2005 Free Software Foundation, Inc. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.1 or any later version published by the Free Software Foundation; with no Invariant Sections, with no Front-Cover Texts, and with no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License”. Chapter 1: Introduction 1 1 Introduction This manual is a work in progress: many sections make no attempt to explain basic concepts in a way suitable for novices. Thus, if you are interested, please get involved in improving this manual. The entire gnu community will benefit. The gnu utilities documented here are mostly compatible with the POSIX standard. Please report bugs to [email protected]. Remember to include the version number, machine architecture, input files, and any other information needed to reproduce the bug: your input, what you expected, what you got, and why it is wrong. Diffs are welcome, but please include a description of the problem as well, since this is sometimes difficult to infer. See section “Bugs” in Using and Porting GNU CC. This manual was originally derived from the Unix man pages in the distributions, which were written by David MacKenzie and updated by Jim Meyering. -

Learning the Bash Shell, 3Rd Edition
1 Learning the bash Shell, 3rd Edition Table of Contents 2 Preface bash Versions Summary of bash Features Intended Audience Code Examples Chapter Summary Conventions Used in This Handbook We'd Like to Hear from You Using Code Examples Safari Enabled Acknowledgments for the First Edition Acknowledgments for the Second Edition Acknowledgments for the Third Edition 1. bash Basics 3 1.1. What Is a Shell? 1.2. Scope of This Book 1.3. History of UNIX Shells 1.3.1. The Bourne Again Shell 1.3.2. Features of bash 1.4. Getting bash 1.5. Interactive Shell Use 1.5.1. Commands, Arguments, and Options 1.6. Files 1.6.1. Directories 1.6.2. Filenames, Wildcards, and Pathname Expansion 1.6.3. Brace Expansion 1.7. Input and Output 1.7.1. Standard I/O 1.7.2. I/O Redirection 1.7.3. Pipelines 1.8. Background Jobs 1.8.1. Background I/O 1.8.2. Background Jobs and Priorities 1.9. Special Characters and Quoting 1.9.1. Quoting 1.9.2. Backslash-Escaping 1.9.3. Quoting Quotation Marks 1.9.4. Continuing Lines 1.9.5. Control Keys 4 1.10. Help 2. Command-Line Editing 2.1. Enabling Command-Line Editing 2.2. The History List 2.3. emacs Editing Mode 2.3.1. Basic Commands 2.3.2. Word Commands 2.3.3. Line Commands 2.3.4. Moving Around in the History List 2.3.5. Textual Completion 2.3.6. Miscellaneous Commands 2.4. vi Editing Mode 2.4.1. -

GPL-3-Free Replacements of Coreutils 1 Contents
GPL-3-free replacements of coreutils 1 Contents 2 Coreutils GPLv2 2 3 Alternatives 3 4 uutils-coreutils ............................... 3 5 BSDutils ................................... 4 6 Busybox ................................... 5 7 Nbase .................................... 5 8 FreeBSD ................................... 6 9 Sbase and Ubase .............................. 6 10 Heirloom .................................. 7 11 Replacement: uutils-coreutils 7 12 Testing 9 13 Initial test and results 9 14 Migration 10 15 Due to the nature of Apertis and its target markets there are licensing terms that 1 16 are problematic and that forces the project to look for alternatives packages. 17 The coreutils package is good example of this situation as its license changed 18 to GPLv3 and as result Apertis cannot provide it in the target repositories and 19 images. The current solution of shipping an old version which precedes the 20 license change is not tenable in the long term, as there are no upgrades with 21 bugfixes or new features for such important package. 22 This situation leads to the search for a drop-in replacement of coreutils, which 23 need to provide compatibility with the standard GNU coreutils packages. The 24 reason behind is that many other packages rely on the tools it provides, and 25 failing to do that would lead to hard to debug failures and many custom patches 26 spread all over the archive. In this regard the strict requirement is to support 27 the features needed to boot a target image with ideally no changes in other 28 components. The features currently available in our coreutils-gplv2 fork are a 29 good approximation. 30 Besides these specific requirements, the are general ones common to any Open 31 Source Project, such as maturity and reliability. -

Answers to Selected Problems
Answers to selected problems Chapter 4 1 Whenever you need to find out information about a command, you should use man. With option -k followed by a keyword, man will display commands related to that keyword. In this case, a suitable keyword would be login, and the dialogue would look like: $ man -k login ... logname (1) - print user’s login name ... The correct answer is therefore logname.Tryit: $ logname chris 3 As in problem 4.1, you should use man to find out more information on date. In this case, however, you need specific information on date, so the command you use is $ man date The manual page for date is likely to be big, but this is not a problem. Remember that the manual page is divided into sections. First of all, notice that under section SYNOPSIS the possible format for arguments to date is given: NOTE SYNOPSIS date [-u] [+format] The POSIX standard specifies only two This indicates that date may have up to two arguments, both of arguments to date – which are optional (to show this, they are enclosed in square some systems may in brackets). The second one is preceded by a + symbol, and if you addition allow others read further down, in the DESCRIPTION section it describes what format can contain. This is a string (so enclose it in quotes) which 278 Answers to selected problems includes field descriptors to specify exactly what the output of date should look like. The field descriptors which are relevant are: %r (12-hour clock time), %A (weekday name), %d (day of week), %B (month name) and %Y (year).