DOCSLIB.ORG

Model 1011 Construction Manual

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Model 1011 Construction Manual M O D E L 1 0 1 1 D i s c r e t e V o l t a g e C o n t r o l l e d O s c i l l a t o r Construction & Operation Guide R E V A - F O R P C B V 1 . 1 S L I G H T L Y N A S T Y E L E C T R O N I C S A D E L A I D E , A U S T R A L I A M O D E L 1 0 1 1 D i s c r e t e O s c i l l a t o r S P E C I F I C A T I O N S PHYSICAL FORM FACTOR: Loudest Warning / 4U WIDTH: 3NMW / 75.5mm HEIGHT: 175mm DEPTH: ~40mm from panel front inc. components PCB: 70 x 150mm, Two-Layer Double Sided CONNECTORS: 4mm Banana IDC power connector pinout. ELECTRICAL POWER: +12V, 0V, -12V CONSUMPTION:~40mA +12V Rail, ~30mA -12V Rail CONNECTOR: IDC 10-pin Shrouded Header, Eurorack Standard or MTA-156 4-Pin Header I/O IMPEDANCES: 100K input, 1K output (nominal) MTA-156 power connector pinout. INPUT RANGES (nominal) 1V/OCT: +/- 10V FM: +/- 5V LOG: +/- 5V SYMMETRY: +/- 5V SYNC: +/- 5V (falling-edge trigger) OUTPUT RANGES (nominal) OUTPUT A: +/- 5V OUTPUT B: +/- 5V SUBOCTAVE: +/- 5V Specifications 2 S L I G H T L Y N A S T Y E L E C T R O N I C S A D E L A I D E , A U S T R A L I A M O D E L 1 0 1 1 D i s c r e t e O s c i l l a t o r T A B L E O F C O N T E N T S SPECIFICATIONS Specifications / Power Requirements 2 INTRODUCTION Introduction 4 CIRCUIT OVERVIEW Circuit Overview 5 Exponential Converter 6 Sawtooth Core 8 Triangle / Sine Shapers 10 Pulse / Suboctave Shapers 10 Output Mixers / Amplifiers 12 CHOOSING COMPONENTS Bill Of Materials (BOM) 14 Choosing Components 15 Transistor Matching 16 CONSTRUCTION Construction Overview 18 Physical Assembly 20 CONTROLS Controls 21 CALIBRATION Calibration Overview 22 CV Scale 23 CV Offset 24 High Frequency Compensation 24 Triangle Adjustment 25 REFERENCE PCB Guide - Lower Board 26 PCB Guide - Upper Board 27 This document is best viewed in dual-page mode. Circuit Overview 3 S L I G H T L Y N A S T Y E L E C T R O N I C S A D E L A I D E , A U S T R A L I A M O D E L 1 0 1 1 D i s c r e t e O s c i l l a t o r I N T R O D U C T I O N The Slightly Nasty Model 1011 is a voltage controlled oscillator that's a little bit different. Despite featuring a host of functionality including four mixable waveshapes, suboctave, linear and logarithmic FM, pulse width modulation, and hard sync, inside it you won't find a single IC opamp or OTA. What you will find is no less than 41 discrete transistors flying in close formation, doing their best to output useable musical tones. The Model 1011 has been designed from the ground up to use modern "jellybean" components that can be cheaply and easily obtained from most electronics suppliers. Despite the unusual implementation, the architecture is actually a very traditional sawtooth-core design that will be familiar to most people who have worked on VCOs before. Three outputs provide mixable sine-triangle, saw-pulse-suboctave, and suboctave square respectively, the pulse wave also featuring both manual and CV-controlled symmetry (pulse width). Aside from the usual 1V/Octave input, there are also separate inputs for both linear and logarithmic FM, each with input attenuators, as well as a hard sync input. The exponential converter is temperature compensated for better thermal stability and the sawtooth core features high-frequency compensation for better pitch tracking. The Model 1011 uses the Loudest Warning 4U format for the front panel, and follows Eurorack electrical and power standards. All front panel components are PCB mounted for easy wiring-free construction. The front panel is available in two finishes - satin anodised and gloss white powdercoat, both on 2.5mm aluminium with robust UV-printed graphics. Introduction 4 S L I G H T L Y N A S T Y E L E C T R O N I C S A D E L A I D E , A U S T R A L I A M O D E L 1 0 1 1 D i s c r e t e O s c i l l a t o r C I R C U I T O V E R V I E W For full schematics, please download the separate schematics PDF. Excerpts shown in this manual may be outdated and are provided for reference only. While the fully populated PCB of the Model 1011 can look quite intimidating, the circuitry can actually be broken down into a set of relatively simple subcircuits that each handle a very specific aspect of the module's operation. Overall, the 1011 has a fairly standard architecture consisting of the following units: 1. Exponential converter - this allows the use of 1V/Octave pitch CVs by taking a linear scale voltage from the CV input and converting it into an exponential scale current to feed the sawtooth core. 2. Sawtooth core - this is the sonic heart of the module, generating the base sawtooth signal from which all other waveshapes are generated. Sync is also implemented in this circuit. 3. Triangle/sine shapers - These convert the raw sawtooth signal into triangle and sine waves by first folding the sawtooth into a triangle shape, and then soft-clipping that to create a pseudo-sine. 4. Pulse/suboctave shapers - These create the pulse wave by feeding the sawtooth signal into a comparator, using the symmetry controls to set the threshold level. The pulse is then used to clock a pulse divider to form the suboctave square. 5. Mixers/output amps - These allow the blending of the various waveforms as well as converting the different levels and offsets of the various raw waveform signals to match the +/-5v expected at the outputs. Block diagram of the Model 1011. Circles marked "A" are attenuators. Circuit Overview 5 S L I G H T L Y N A S T Y E L E C T R O N I C S A D E L A I D E , A U S T R A L I A Circuit Overview 6 S L I G H T L Y N A S T Y E L E C T R O N I C S A D E L A I D E , A U S T R A L I A M O D E L 21 02 13 11 A s y m mDei ts rcirce tSel eOws cLiilml ai t oe r E X P O N E N T I A L C O N V E R T E R Undoubtedly the finickiest part of most VCOs, the exponential converter in the VCC 8 Model 1011 is essentially a discrete reimplementation of the opamp-stabilised 3 + V+ 1 transistor pair found in countless other designs. This circuit works by using the 2 - V- GND naturally exponential relationship of a transistor's base-emitter voltage to its 4 output current, using two matched transistors to mostly cancel out each others' VEE R3 thermal effects and keep the conversion stable across different temperatures and 3 3 currents. A feedback-stabilised current source on the shared emitters of the 1V/OCT R1 1 1 2 2 transistors holds one transistor at a constant current, causing the exponential GND TEMPCO current caused by changes to the input voltage to appear at the collector of the R2 other one. A temperature-sensitive "tempco" resistor provides additional GND correction to the aspects of the circuit's thermal response that are not cancelled VEE TO_CORE by the matched pair. The exact operation of this sort of converter is a bit too involved to get into in this Traditional configuration of PNP exponential converter with opamp manual, but an excellent rundown of the basic principles can be found on René current source. Schmitz' website at http://schmitzbits.de/expo_tutorial/index.html In the 1011, the exponential converter can be broken down further into three basic sections. There are the frontend buffer/amplifiers that combine the various CVs and panel controls into a single pitch voltage; the exponentiator itself, in the form of the matched pair; and the feedback controlled current source, which consists of a differential pair controlling a current source tranistor. The bulk of the exponentiator is single rail and works between 0v and +VCC. The input buffer/amplifiers are essentially just crude emitter followers, and consist of transistors Q501, Q502, and Q510 along with their respective passive components. The output of Q501 and Q502 are both combined and go through the voltage divider comprised of RV505 and the tempco resistor R522, in order to reduce the level to the small voltage swing needed for the exponentiator. Because the circuit is single rail, Q503 provides a buffered offset voltage so that the resultant scaled CV is centred near the 1/2 VCC mark.
Load more

Recommended publications
  • Moogerfooger® MF-107 Freqbox™
    Understanding and Using your moogerfooger® MF-107 FreqBox™ TABLE OF CONTENTS Introduction.................................................2 Getting Started Right Away!.......................4 Basic Applications......................................6 FreqBox Theory........................................10 FreqBox Functions....................................16 Advanced Applications.............................21 Technical Information...............................24 Limited Warranty......................................25 MF-107 Specifications..............................26 1 Welcome to the world of moogerfooger® Analog Effects Modules. Your Model MF-107 FreqBox™ is a rugged, professional-quality instrument, designed to be equally at home on stage or in the studio. Its great sound comes from the state-of-the- art analog circuitry, designed and built by the folks at Moog Music in Asheville, NC. Your MF-107 FreqBox is a direct descendent of the original modular Moog® synthesizers. It contains several complete modular synth functions: a voltage-controlled oscillator (VCO) with variable waveshape, capable of being hard synced and frequency modulated by the audio input, and an envelope follower which allows the dynamics of the input signal to modulate the frequency of the VCO. In addition the amplitude of the VCO is controlled by the dynamics of the input signal, and the VCO can be mixed with the audio input. All performance parameters are voltage-controllable, which means that you can use expression pedals, MIDI-to-CV converter, or any other source of control voltages to 'play' your MF-107. Control voltage outputs mean that the MF-107 can be used with other moogerfoogers or voltage controlled devices like the Minimoog Voyager® or Little Phatty® synthesizers. While you can use it on the floor as a conventional effects box, your MF-107 FreqBox is much more versatile and its sound quality is higher than the single fixed function "stomp boxes" that you may be accustomed to.
    [Show full text]
  • Pulse Width Modulation
    International Journal of Research in Engineering, Science and Management 38 Volume-2, Issue-12, December-2019 www.ijresm.com | ISSN (Online): 2581-5792 Pulse Width Modulation M. Naganetra1, R. Ramya2, D. Rohini3 1,2,3Student, Dept. of Electronics & Communication Engineering, K. S. Institute of Technology, Bengaluru India Abstract: This paper presents pulse width modulation which can 2. Principle be controlled by duty cycle. Pulse width modulation(PWM) is a Pulse width modulation uses a rectangular pulse wave powerful technique for controlling analog circuits with a digital signal. PWM is widely used in different applications, ranging from whose pulse width is modulated resulting in the variation of the measurement and communications to power control and average value of the waveform. If we consider a pulse signal conversions, which transforms the amplitude bounded input f(t), with period T, low value Y-min, high value Y-max and a signals into the pulse width output signal without suffering noise duty cycle D. Average value of the output signal is given by, quantization. The frequency of output signal is usually constant. By controlling analog circuits digitally, system cost and power 1 푇 푦̅= ∫ 푓(푡)푑푡 consumption can be reduced. The PWM signal is still digital 푇 0 because, at any instant of time, the full DC supply will be either fully_ ON or fully _OFF. Given a sufficient bandwidth, any analog 3. PWM generator signals (sine, square, triangle and so on) can be encoded with PWM. Keywords: decrease-duty, duty cycle, increase-duty, PWM (pulse width modulation), RTL view 1. Introduction Pulse width modulation (or pulse duration modulation) is a method of reducing the average power delivered by an electrical Fig.
    [Show full text]
  • How Can You Replicate Real World Signals? Precisely
    How can you replicate real world signals? Precisely tç)[UP.)[ 7QQ PSDIBOOFMT FG400 Series t*OUVJUJWFPQFSBUJPOXJUIBw Arbitrary/Function Generator LCD screen t4ZODISPOJ[FVQUPVOJUTUP QSPWJEFVQUPPVUQVU DIBOOFMT t"WBSJFUZPGTXFFQTBOE modulations Bulletin FG400-01EN Features and benefits FG400 Series Features and CFOFýUT &BTJMZHFOFSBUFCBTJD BQQMJDBUJPOTQFDJýDBOEBSCJUSBSZXBWFGPSNT 2 The FG400 Arbitrary/Function Generator provides a wide variety of waveforms as standard and generates signals simply and easily. There are one channel (FG410) and two channel (FG420) models. As the output channels are isolated, an FG400 can also be used in the development of floating circuits. (up to 42 V) Basic waveforms Advanced functions 4JOF DC 4XFFQ.PEVMBUJPO Burst 0.01 μHz to 30 MHz ±10 V/open Frequency sweep "VUP Setting items Oscillation and stop are 4RVBSF start/stop frequency, time, mode automatically repeated with the (continuous, single, gated single), respectively specified wave number. function (one-way/shuttle, linear/ log) 0.01 μHz to 15 MHz, variable duty Pulse 18. Trigger Setting items Oscillation with the specified wave carrier duty, peak duty deviation number is done each time a trigger Output duty is received. the range of carrier duty ±peak duty deviation 0.01 μHz to 15 MHz, variable leading/trailing edge time Ramp ". Gate Setting items Oscillation is done in integer cycles carrier amplitude, modulation depth or half cycles while the gate is on. Output amp. the range of amp./2 × (1 ±mod. 0.01 μHz to 5 MHz, variable symmetry Depth/100) 3 For trouble shooting Arbitrary waveforms (16 bits amplitude resolution) of up to 512 K words per waveform can be generated. 128 waveforms with a total size of 4 M words can be saved to the internal non-volatile memory.
    [Show full text]
  • The 1-Bit Instrument: the Fundamentals of 1-Bit Synthesis
    BLAKE TROISE The 1-Bit Instrument The Fundamentals of 1-Bit Synthesis, Their Implementational Implications, and Instrumental Possibilities ABSTRACT The 1-bit sonic environment (perhaps most famously musically employed on the ZX Spectrum) is defined by extreme limitation. Yet, belying these restrictions, there is a surprisingly expressive instrumental versatility. This article explores the theory behind the primary, idiosyncratically 1-bit techniques available to the composer-programmer, those that are essential when designing “instruments” in 1-bit environments. These techniques include pulse width modulation for timbral manipulation and means of generating virtual polyph- ony in software, such as the pin pulse and pulse interleaving techniques. These methodologies are considered in respect to their compositional implications and instrumental applications. KEYWORDS chiptune, 1-bit, one-bit, ZX Spectrum, pulse pin method, pulse interleaving, timbre, polyphony, history 2020 18 May on guest by http://online.ucpress.edu/jsmg/article-pdf/1/1/44/378624/jsmg_1_1_44.pdf from Downloaded INTRODUCTION As unquestionably evident from the chipmusic scene, it is an understatement to say that there is a lot one can do with simple square waves. One-bit music, generally considered a subdivision of chipmusic,1 takes this one step further: it is the music of a single square wave. The only operation possible in a -bit environment is the variation of amplitude over time, where amplitude is quantized to two states: high or low, on or off. As such, it may seem in- tuitively impossible to achieve traditionally simple musical operations such as polyphony and dynamic control within a -bit environment. Despite these restrictions, the unique tech- niques and auditory tricks of contemporary -bit practice exploit the limits of human per- ception.
    [Show full text]
  • Tracking of High-Speed, Non-Smooth and Microscale-Amplitude Wave Trajectories
    Tracking of High-speed, Non-smooth and Microscale-amplitude Wave Trajectories Jiradech Kongthon Department of Mechatronics Engineering, Assumption University, Suvarnabhumi Campus, Samuthprakarn, Thailand Keywords: High-speed Tracking, Inversion-based Control, Microscale Positioning, Reduced-order Inverse, Tracking. Abstract: In this article, an inversion-based control approach is proposed and presented for tracking desired trajectories with high-speed (100Hz), non-smooth (triangle and sawtooth waves), and microscale-amplitude (10 micron) wave forms. The interesting challenge is that the tracking involves the trajectories that possess a high frequency, a microscale amplitude, sharp turnarounds at the corners. Two different types of wave trajectories, which are triangle and sawtooth waves, are investigated. The model, or the transfer function of a piezoactuator is obtained experimentally from the frequency response by using a dynamic signal analyzer. Under the inversion-based control scheme and the model obtained, the tracking is simulated in MATLAB. The main contributions of this work are to show that (1) the model and the controller achieve a good tracking performance measured by the root mean square error (RMSE) and the maximum error (Emax), (2) the maximum error occurs at the sharp corner of the trajectories, (3) tracking the sawtooth wave yields larger RMSE and Emax values,compared to tracking the triangle wave, and (4) in terms of robustness to modeling error or unmodeled dynamics, Emax is still less than 10% of the peak to peak amplitude of 20 micron if the increases in the natural frequency and the damping ratio are less than 5% for the triangle trajectory and Emax is still less than 10% of the peak to peak amplitude of 20 micron if the increases in the natural frequency and the damping ratio are less than 3.2 % for the sawtooth trajectory.
    [Show full text]
  • Contribution of the Conditioning Stage to the Total Harmonic Distortion in the Parametric Array Loudspeaker
    Universidad EAFIT Contribution of the conditioning stage to the Total Harmonic Distortion in the Parametric Array Loudspeaker Andrés Yarce Botero Thesis to apply for the title of Master of Science in Applied Physics Advisor Olga Lucia Quintero. Ph.D. Master of Science in Applied Physics Science school Universidad EAFIT Medellín - Colombia 2017 1 Contents 1 Problem Statement 7 1.1 On sound artistic installations . 8 1.2 Objectives . 12 1.2.1 General Objective . 12 1.2.2 Specific Objectives . 12 1.3 Theoretical background . 13 1.3.1 Physics behind the Parametric Array Loudspeaker . 13 1.3.2 Maths behind of Parametric Array Loudspeakers . 19 1.3.3 About piezoelectric ultrasound transducers . 21 1.3.4 About the health and safety uses of the Parametric Array Loudspeaker Technology . 24 2 Acquisition of Sound from self-demodulation of Ultrasound 26 2.1 Acoustics . 26 2.1.1 Directionality of Sound . 28 2.2 On the non linearity of sound . 30 2.3 On the linearity of sound from ultrasound . 33 3 Signal distortion and modulation schemes 38 3.1 Introduction . 38 3.2 On Total Harmonic Distortion . 40 3.3 Effects on total harmonic distortion: Modulation techniques . 42 3.4 On Pulse Wave Modulation . 46 4 Loudspeaker Modelling by statistical design of experiments. 49 4.1 Characterization Parametric Array Loudspeaker . 51 4.2 Experimental setup . 52 4.2.1 Results of PAL radiation pattern . 53 4.3 Design of experiments . 56 4.3.1 Placket Burmann method . 59 4.3.2 Box Behnken methodology . 62 5 Digital filtering techniques and signal distortion analysis.
    [Show full text]
  • Verified Design Analog Pulse Width Modulation
    John Caldwell TI Precision Designs: Verified Design Analog Pulse Width Modulation TI Precision Designs Circuit Description TI Precision Designs are analog solutions created by This circuit utilizes a triangle wave generator and TI’s analog experts. Verified Designs offer the theory, comparator to generate a pulse-width-modulated component selection, simulation, complete PCB (PWM) waveform with a duty cycle that is inversely schematic & layout, bill of materials, and measured proportional to the input voltage. An op amp and performance of useful circuits. Circuit modifications comparator generate a triangular waveform which is that help to meet alternate design goals are also passed to the inverting input of a second comparator. discussed. By passing the input voltage to the non-inverting comparator input, a PWM waveform is produced. Negative feedback of the PWM waveform to an error amplifier is utilized to ensure high accuracy and linearity of the output Design Resources Ask The Analog Experts Design Archive All Design files WEBENCH® Design Center TINA-TI™ SPICE Simulator TI Precision Designs Library OPA2365 Product Folder TLV3502 Product Folder REF3325 Product Folder R4 C1 VCC R3 - VPWM + VIN VREF R1 + ++ + U1A - U2A V R2 C2 CC VTRI C3 R7 - ++ U1B VREF VCC VREF - ++ U2B VCC R6 R5 An IMPORTANT NOTICE at the end of this TI reference design addresses authorized use, intellectual property matters and other important disclaimers and information. TINA-TI is a trademark of Texas Instruments WEBENCH is a registered trademark of Texas Instruments SLAU508-June 2013-Revised June 2013 Analog Pulse Width Modulation 1 Copyright © 2013, Texas Instruments Incorporated www.ti.com 1 Design Summary The design requirements are as follows: Supply voltage: 5 Vdc Input voltage: -2 V to +2 V, dc coupled Output: 5 V, 500 kHz PWM Ideal transfer function: V The design goals and performance are summarized in Table 1.
    [Show full text]
  • The Oscilloscope and the Function Generator: Some Introductory Exercises for Students in the Advanced Labs
    The Oscilloscope and the Function Generator: Some introductory exercises for students in the advanced labs Introduction So many of the experiments in the advanced labs make use of oscilloscopes and function generators that it is useful to learn their general operation. Function generators are signal sources which provide a specifiable voltage applied over a specifiable time, such as a \sine wave" or \triangle wave" signal. These signals are used to control other apparatus to, for example, vary a magnetic field (superconductivity and NMR experiments) send a radioactive source back and forth (M¨ossbauer effect experiment), or act as a timing signal, i.e., \clock" (phase-sensitive detection experiment). Oscilloscopes are a type of signal analyzer|they show the experimenter a picture of the signal, usually in the form of a voltage versus time graph. The user can then study this picture to learn the amplitude, frequency, and overall shape of the signal which may depend on the physics being explored in the experiment. Both function generators and oscilloscopes are highly sophisticated and technologically mature devices. The oldest forms of them date back to the beginnings of electronic engineering, and their modern descendants are often digitally based, multifunction devices costing thousands of dollars. This collection of exercises is intended to get you started on some of the basics of operating 'scopes and generators, but it takes a good deal of experience to learn how to operate them well and take full advantage of their capabilities. Function generator basics Function generators, whether the old analog type or the newer digital type, have a few common features: A way to select a waveform type: sine, square, and triangle are most common, but some will • give ramps, pulses, \noise", or allow you to program a particular arbitrary shape.
    [Show full text]
  • The Differential Pair As a Triangle-Sine Wave Converter V - ROBERT G
    418 IEEE JOURNAL OF SOLID-STATE CIRCUITS, JUNE 1976 Correspondence The Differential Pair as a Triangle-Sine Wave Converter v - ROBERT G. MEYER, WILLY M. C. SANSEN, SIK LUI, AND STEFAN PEETERS R~ R~ 1 / Abstract–The performance of a differential pair with emitter degen- eration as a triangle-sine wave converter is analyzed. Equations describ- ing the circuit operation are derived and solved both analytically and by computer. This allows selection of operating conditions for optimum performance such that total harmonic distortion as low as 0.2 percent “- has been measured. -vEE (a) I. INTRODUCTION The conversion of ttiangle waves to sine waves is a function I ---- I- often required in waveshaping circuits. For example, the oscil- lators used in function generators usually generate triangular output waveforms [ 1] because of the ease with which such oscillators can operate over a wide frequency range including very low frequencies. This situation is also common in mono- r v, Zr t lithic oscillators [2] . Sinusoidal outputs are commonly de- sired in such oscillators and can be achieved by use of a non- linear circuit which produces an output sine wave from an input triangle wave. — — — — The above circuit function has been realized in the past by -I -I ----- means of a piecewise linear approximation using diode shaping J ‘“b ‘M VI networks [ 1] . However, a simpler approach and one well M suited to monolithic realization has been suggested by Grebene [3] . This is shown in Fig. 1 and consists simply of a differen- 77 tial pair with an appropriate value of emitter resistance R.
    [Show full text]
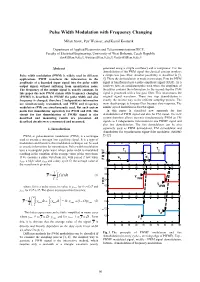
  • Pulse Width Modulation with Frequency Changing
    Pulse Width Modulation with Frequency Changing Milan Stork, Petr Weissar, and Kamil Kosturik Department of Applied Electronics and Telecommunications/RICE, Faculty of Electrical Engineering, Umiversity of West Bohemia, Czech Republic [email protected], [email protected], [email protected] Abstract generated using a simple oscillator) and a comparator. For the demodulation of the PWM signal the classical concept employs Pulse width modulation (PWM) is widely used in different a simple low pass filter. Another possibility is described in [3, applications. PWM transform the information in the 4]. There the demodulation is made in two steps. First the PWM amplitude of a bounded input signal into the pulse width signal is transformed into a pulse amplitude signal (PAM). As a output signal, without suffering from quantization noise. result we have an equidistant pulse train where the amplitude of The frequency of the output signal is usually constant. In the pulses contains the information. In the second step the PAM this paper the new PWM system with frequency changing signal is processed with a low pass filter. This reconstructs the (PWMF) is described. In PWMF the pulse width and also original signal waveform. These two step demodulation is frequency is changed, therefore 2 independents information exactly the reverse way to the uniform sampling process. The are simultaneously transmitted, and PWM and frequency main disadvantage is lowpass filter because slow response. The modulation (FM) are simultaneously used. But such system similar (speed limitation) is for FM signal. needs fast demodulator separately for PWM and FM. The In this paper is described new approach for fast circuit for fast demodulation of PWMF signal is also demodulation of PWM signal and also for FM signal.
    [Show full text]
  • ICL8038 TM D FO NDE MME ECO OT R N Data Sheet April 2001 File Number 2864.4
    NS ESIG W D R NE ICL8038 TM D FO NDE MME ECO OT R N Data Sheet April 2001 File Number 2864.4 Precision Waveform Generator/Voltage Features Controlled Oscillator • Low Frequency Drift with Temperature...... 250ppm/oC The ICL8038 waveform generator is a monolithic integrated • LowDistortion...............1%(SineWaveOutput) tle circuit capable of producing high accuracy sine, square, 80 triangular, sawtooth and pulse waveforms with a minimum of • HighLinearity ...........0.1%(Triangle Wave Output) external components. The frequency (or repetition rate) can • Wide Frequency Range ............0.001Hzto300kHz - be selected externally from 0.001Hz to more than 300kHz using either resistors or capacitors, and frequency • VariableDutyCycle.....................2%to98% modulation and sweeping can be accomplished with an • HighLevelOutputs......................TTLto28V ci- external voltage. The ICL8038 is fabricated with advanced • Simultaneous Sine, Square, and Triangle Wave monolithic technology, using Schottky barrier diodes and thin Outputs e- film resistors, and the output is stable over a wide range of temperature and supply variations. These devices may be • Easy to Use - Just a Handful of External Components er- interfaced with phase locked loop circuitry to reduce Required o /Vo temperature drift to less than 250ppm/ C. e - Ordering Information ed PART NUMBER STABILITY TEMP. RANGE (oC) PACKAGE PKG. NO. il- o r) ICL8038CCPD 250ppm/ C(Typ) 0to70 14LdPDIP E14.3 tho ICL8038CCJD 250ppm/oC(Typ) 0to70 14LdCERDIP F14.3 ICL8038BCJD 180ppm/oC(Typ)
    [Show full text]
  • Chapter 9. Fourier Series A. the Fourier Sine Series
    Vector Spaces in Physics 8/6/2015 Chapter 9. Fourier Series A. The Fourier Sine Series The general solution. In Chapter 8 we found solutions to the wave equation for a string fixed at both ends, of length L, and with wave velocity v, yn x, t A n sin k n x cos n t k n n L 1 n 2L , n = 1, 2, 3, . (9-1) n v n n L v fn n 2L We are now going to proceed to describe an arbitrary motion of the string with both ends fixed in terms of a linear superposition of normal modes: nx general solution, string , (9-2) y x, t Ann sin cos t n1 L fixed at both ends nv where and the coefficients An are to be determined. Here are some things to be noted: n L (1) We are assuming for the moment that this equation is true - that is, in the limit where we include an infinite number of terms, that the infinite series is an arbitrarily good approximation to the solution y x, t . (2) Each term in the series is separately a solution to the wave equation satisfying the boundary conditions, and so the series sum itself is such a solution. (3) This series is sort of like an expansion of a vector in terms of a set of basis vectors. In this picture the coefficients An are the coordinates of the function . (4) We still have to specify initial conditions and find a method to ensure that they are satisfied.
    [Show full text]