DOCSLIB.ORG

Functional Waveforms for Electronics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Functional Waveforms for Electronics 4/6/2017 Functional Waveforms for Electronics Lesson 16 EET 150 Learning Objectives In this lesson you will: see typical waveforms used in electronic circuits learn how to identify these waveforms by their shape identify the amplitudes of these waves learn where these waves are used see what instruments can produce and measure waveforms 1 4/6/2017 Common Waveforms-Sine Wave Sine Waveform 3 3 Characteristics 2 Amplitude Measures RMS 1 Peak Peak-to-peak value Peak v(t) 0 to Peak value Amplitude Amplitude Peak 1 Measured with zero reference 2 3 Root Mean Square 3 0 2 4 6 8 10 (RMS) Value 0 t 10 Time 0.707 of Peak Value RMS factor of 0.707 only valid for Sine waves Sine waves used to test amplifiers Common Waveforms-Sine Wave Example What is peak-to-peak value of the waveform shown? What is peak 1.414 value of the V RMS 2 Vp waveform shown? 4 Vpp What is RMS value of the waveform shown? VRMS =0.707(2) VRMS = 1.414 V 2 4/6/2017 Common Waveforms-Sine Wave Sine wave with DC offset DC offset Sine Waveform raises entire 6 6 wave above zero 4 2.5 Waveform v(t) 2 Symmetric about 2.5 Amplitude +2.5 0 DC offsets can 2 be either 3 positive or 0 2 4 6 8 10 negative 0 t 10 Time Common Waveforms-Square Wave Square Wave Voltage Measures 3 3 Peak-to-peak value RMS 2 Peak value 1 Peak Peak Measured with zero s(t) to reference 0 Peak Amplitude 1 Root Mean Square (RMS) Value 2 3 Equals peak value 3 0 2 4 6 8 10 0 t 10 Square wave can Time Be off set with DC 3 4/6/2017 Common Waveforms-Pulse Train Pulse Train has only positive values Signal used in computer circuits. For this signal, half period is on- half period off Adding DC off set to square wave produces pulse Common Waveforms-Pulse Train Pulse Train 5 Voltage Measures 4 Peak-to-peak value RMS Peak value Peak 2 to Peak Peak Peak value = peak- s(t) to-peak value Amplitude 0 Root Mean Square (RMS) Value 2 A 3 RMS 0 2 4 6 8 10 2 0 t 10 Tim e A = peak amplitude value 4 4/6/2017 Common Waveforms-Ramp Waves Ramp waves increase linearly, reset, then repeat Ramp waves used to move trace in scopes Used to control and sweep frequency linearly Dc off set can move waveform up or down Common Waveforms-Ramp Waves 8 Voltage Measures 8 Peak-to-peak value 4 Peak Peak value RMS Peak to Peak Peak value = peak- v(t) 0 to-peak value Amplitude Root Mean Square 4 (RMS) Value A 8 8 RMS 0 3 6 9 12 15 3 0 t 15 Tim e A = peak amplitude value 5 4/6/2017 Common Waveforms-Ramp Waves Ramp wave with negative dc off set Negative Dc off set lowers half of wave below zero 3 v 6 V RMS value of off set wave not equal to wave without offset Common Waveforms-Triangle Waves Triangle waves increase linearly then decrease linearly at a given frequency Waveform used in pulse-width modulators Note: this waveform is all positive It can be lowered or raised using DC off set 6 4/6/2017 Common Waveforms-Triangle Waves Off set triangle wave This wave has equal positive and negative values Off set equals Amplitude/2 Common Waveforms-Triangle Waves Voltage Measures Peak-to-peak value 6.5 6 T Peak value 4 6 V A 3.46 2 6 V Peak value = peak- to-peak value 2 vv(t) Amplitude Root Mean Square 0 (RMS) Value A 2 A RMS 2 3.5 3 0 2 4 6 8 10 12 14 16 0 t 16 Tim e A = peak amplitude value 7 4/6/2017 Measuring Waveform Amplitudes An oscilloscope can measure A DVM can measure and all waveform amplitudes display RMS values and frequency Use an oscilloscope to verify DVM frequency limits waveform generator outputs Use “True RMS” for non-sinusoids Producing Electronic Waveforms An instrument called a function generator produces all the waveforms covered in this presentation Front Panel Instrument Back 8 4/6/2017 End Lesson 16 EET 150 Coming Next: MORE WAVEFORM CHARACTERISTICS 9 .
Load more

Recommended publications
  • Chapter 73 Mean and Root Mean Square Values
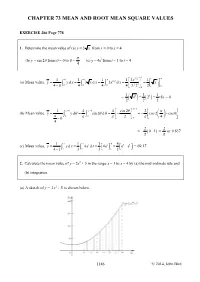
    CHAPTER 73 MEAN AND ROOT MEAN SQUARE VALUES EXERCISE 286 Page 778 1. Determine the mean value of (a) y = 3 x from x = 0 to x = 4 π (b) y = sin 2θ from θ = 0 to θ = (c) y = 4et from t = 1 to t = 4 4 3/2 4 44 4 4 1 1 11/2 13x 13 (a) Mean value, y= ∫∫ yxd3d3d= xx= ∫ x x= = x − 00 0 0 4 0 4 4 4 3/20 2 1 11 = 433=( 2) = (8) = 4 2( ) 22 π /4 1 ππ/4 4 /4 4 cos 2θπ 2 (b) Mean value, yy=dθ = sin 2 θθ d =−=−−cos 2 cos 0 π ∫∫00ππ24 π − 0 0 4 2 2 = – (01− ) = or 0.637 π π 144 1 144 (c) Mean value, y= yxd= 4ett d t = 4e = e41 − e = 69.17 41− ∫∫11 3 31 3 2. Calculate the mean value of y = 2x2 + 5 in the range x = 1 to x = 4 by (a) the mid-ordinate rule and (b) integration. (a) A sketch of y = 25x2 + is shown below. 1146 © 2014, John Bird Using 6 intervals each of width 0.5 gives mid-ordinates at x = 1.25, 1.75, 2.25, 2.75, 3.25 and 3.75, as shown in the diagram x 1.25 1.75 2.25 2.75 3.25 3.75 y = 25x2 + 8.125 11.125 15.125 20.125 26.125 33.125 Area under curve between x = 1 and x = 4 using the mid-ordinate rule with 6 intervals ≈ (width of interval)(sum of mid-ordinates) ≈ (0.5)( 8.125 + 11.125 + 15.125 + 20.125 + 26.125 + 33.125) ≈ (0.5)(113.75) = 56.875 area under curve 56.875 56.875 and mean value = = = = 18.96 length of base 4− 1 3 3 4 44 1 1 2 1 2x 1 128 2 (b) By integration, y= yxd = 2 x + 5 d x = +5 x = +20 −+ 5 − ∫∫11 41 3 3 31 3 3 3 1 = (57) = 19 3 This is the precise answer and could be obtained by an approximate method as long as sufficient intervals were taken 3.
    [Show full text]
  • Tracking of High-Speed, Non-Smooth and Microscale-Amplitude Wave Trajectories
    Tracking of High-speed, Non-smooth and Microscale-amplitude Wave Trajectories Jiradech Kongthon Department of Mechatronics Engineering, Assumption University, Suvarnabhumi Campus, Samuthprakarn, Thailand Keywords: High-speed Tracking, Inversion-based Control, Microscale Positioning, Reduced-order Inverse, Tracking. Abstract: In this article, an inversion-based control approach is proposed and presented for tracking desired trajectories with high-speed (100Hz), non-smooth (triangle and sawtooth waves), and microscale-amplitude (10 micron) wave forms. The interesting challenge is that the tracking involves the trajectories that possess a high frequency, a microscale amplitude, sharp turnarounds at the corners. Two different types of wave trajectories, which are triangle and sawtooth waves, are investigated. The model, or the transfer function of a piezoactuator is obtained experimentally from the frequency response by using a dynamic signal analyzer. Under the inversion-based control scheme and the model obtained, the tracking is simulated in MATLAB. The main contributions of this work are to show that (1) the model and the controller achieve a good tracking performance measured by the root mean square error (RMSE) and the maximum error (Emax), (2) the maximum error occurs at the sharp corner of the trajectories, (3) tracking the sawtooth wave yields larger RMSE and Emax values,compared to tracking the triangle wave, and (4) in terms of robustness to modeling error or unmodeled dynamics, Emax is still less than 10% of the peak to peak amplitude of 20 micron if the increases in the natural frequency and the damping ratio are less than 5% for the triangle trajectory and Emax is still less than 10% of the peak to peak amplitude of 20 micron if the increases in the natural frequency and the damping ratio are less than 3.2 % for the sawtooth trajectory.
    [Show full text]
  • Verified Design Analog Pulse Width Modulation
    John Caldwell TI Precision Designs: Verified Design Analog Pulse Width Modulation TI Precision Designs Circuit Description TI Precision Designs are analog solutions created by This circuit utilizes a triangle wave generator and TI’s analog experts. Verified Designs offer the theory, comparator to generate a pulse-width-modulated component selection, simulation, complete PCB (PWM) waveform with a duty cycle that is inversely schematic & layout, bill of materials, and measured proportional to the input voltage. An op amp and performance of useful circuits. Circuit modifications comparator generate a triangular waveform which is that help to meet alternate design goals are also passed to the inverting input of a second comparator. discussed. By passing the input voltage to the non-inverting comparator input, a PWM waveform is produced. Negative feedback of the PWM waveform to an error amplifier is utilized to ensure high accuracy and linearity of the output Design Resources Ask The Analog Experts Design Archive All Design files WEBENCH® Design Center TINA-TI™ SPICE Simulator TI Precision Designs Library OPA2365 Product Folder TLV3502 Product Folder REF3325 Product Folder R4 C1 VCC R3 - VPWM + VIN VREF R1 + ++ + U1A - U2A V R2 C2 CC VTRI C3 R7 - ++ U1B VREF VCC VREF - ++ U2B VCC R6 R5 An IMPORTANT NOTICE at the end of this TI reference design addresses authorized use, intellectual property matters and other important disclaimers and information. TINA-TI is a trademark of Texas Instruments WEBENCH is a registered trademark of Texas Instruments SLAU508-June 2013-Revised June 2013 Analog Pulse Width Modulation 1 Copyright © 2013, Texas Instruments Incorporated www.ti.com 1 Design Summary The design requirements are as follows: Supply voltage: 5 Vdc Input voltage: -2 V to +2 V, dc coupled Output: 5 V, 500 kHz PWM Ideal transfer function: V The design goals and performance are summarized in Table 1.
    [Show full text]
  • The Oscilloscope and the Function Generator: Some Introductory Exercises for Students in the Advanced Labs
    The Oscilloscope and the Function Generator: Some introductory exercises for students in the advanced labs Introduction So many of the experiments in the advanced labs make use of oscilloscopes and function generators that it is useful to learn their general operation. Function generators are signal sources which provide a specifiable voltage applied over a specifiable time, such as a \sine wave" or \triangle wave" signal. These signals are used to control other apparatus to, for example, vary a magnetic field (superconductivity and NMR experiments) send a radioactive source back and forth (M¨ossbauer effect experiment), or act as a timing signal, i.e., \clock" (phase-sensitive detection experiment). Oscilloscopes are a type of signal analyzer|they show the experimenter a picture of the signal, usually in the form of a voltage versus time graph. The user can then study this picture to learn the amplitude, frequency, and overall shape of the signal which may depend on the physics being explored in the experiment. Both function generators and oscilloscopes are highly sophisticated and technologically mature devices. The oldest forms of them date back to the beginnings of electronic engineering, and their modern descendants are often digitally based, multifunction devices costing thousands of dollars. This collection of exercises is intended to get you started on some of the basics of operating 'scopes and generators, but it takes a good deal of experience to learn how to operate them well and take full advantage of their capabilities. Function generator basics Function generators, whether the old analog type or the newer digital type, have a few common features: A way to select a waveform type: sine, square, and triangle are most common, but some will • give ramps, pulses, \noise", or allow you to program a particular arbitrary shape.
    [Show full text]
  • True RMS, Trueinrush®, and True Megohmmeter®
    “WATTS CURRENT” TECHNICAL BULLETIN Issue 09 Summer 2016 True RMS, TrueInRush®, and True Megohmmeter ® f you’re a user of AEMC® instruments, you may have come across the terms True IRMS, TrueInRush®, and/or True Megohmmeter ®. In this article, we’ll briefly define what these terms mean and why they are important to you. True RMS The most well-known of these is True RMS, an industry term for a method for calculating Root Mean Square. Root Mean Square, or RMS, is a mathematical concept used to derive the average of a constantly varying value. In electronics, RMS provides a way to measure effective AC power that allows you to compare it to the equivalent heating value of a DC system. Some low-end instruments employ a technique known as “average sensing,” sometimes referred to as “average RMS.” This entails multiplying the peak AC voltage or current by 0.707, which represents the decimal form of one over the square root of two. For electrical systems where the AC cycle is sinusoidal and reasonably undistorted, this can produce accurate and reliable results. Unfortunately, for other AC waveforms, such as square waves, this calculation can introduce significant inaccuracies. The equation can also be problematic when the AC wave is non-linear, as would be found in systems where the original or fundamental wave is distorted by one or more harmonic waves. In these cases, we need to apply a method known as “true” RMS. This involves a more generalized mathematical calculation that takes into consideration all irregularities and asymmetries that may be present in the AC waveform: In this equation, n equals the number of measurements made during one complete cycle of the waveform.
    [Show full text]
  • The Differential Pair As a Triangle-Sine Wave Converter V - ROBERT G
    418 IEEE JOURNAL OF SOLID-STATE CIRCUITS, JUNE 1976 Correspondence The Differential Pair as a Triangle-Sine Wave Converter v - ROBERT G. MEYER, WILLY M. C. SANSEN, SIK LUI, AND STEFAN PEETERS R~ R~ 1 / Abstract–The performance of a differential pair with emitter degen- eration as a triangle-sine wave converter is analyzed. Equations describ- ing the circuit operation are derived and solved both analytically and by computer. This allows selection of operating conditions for optimum performance such that total harmonic distortion as low as 0.2 percent “- has been measured. -vEE (a) I. INTRODUCTION The conversion of ttiangle waves to sine waves is a function I ---- I- often required in waveshaping circuits. For example, the oscil- lators used in function generators usually generate triangular output waveforms [ 1] because of the ease with which such oscillators can operate over a wide frequency range including very low frequencies. This situation is also common in mono- r v, Zr t lithic oscillators [2] . Sinusoidal outputs are commonly de- sired in such oscillators and can be achieved by use of a non- linear circuit which produces an output sine wave from an input triangle wave. — — — — The above circuit function has been realized in the past by -I -I ----- means of a piecewise linear approximation using diode shaping J ‘“b ‘M VI networks [ 1] . However, a simpler approach and one well M suited to monolithic realization has been suggested by Grebene [3] . This is shown in Fig. 1 and consists simply of a differen- 77 tial pair with an appropriate value of emitter resistance R.
    [Show full text]
  • Basic Statistics = ∑
    Basic Statistics, Page 1 Basic Statistics Author: John M. Cimbala, Penn State University Latest revision: 26 August 2011 Introduction The purpose of this learning module is to introduce you to some of the fundamental definitions and techniques related to analyzing measurements with statistics. In all the definitions and examples discussed here, we consider a collection (sample) of measurements of a steady parameter. E.g., repeated measurements of a temperature, distance, voltage, etc. Basic Definitions for Data Analysis using Statistics First some definitions are necessary: o Population – the entire collection of measurements, not all of which will be analyzed statistically. o Sample – a subset of the population that is analyzed statistically. A sample consists of n measurements. o Statistic – a numerical attribute of the sample (e.g., mean, median, standard deviation). Suppose a population – a series of measurements (or readings) of some variable x is available. Variable x can be anything that is measurable, such as a length, time, voltage, current, resistance, etc. Consider a sample of these measurements – some portion of the population that is to be analyzed statistically. The measurements are x1, x2, x3, ..., xn, where n is the number of measurements in the sample under consideration. The following represent some of the statistics that can be calculated: 1 n Mean – the sample mean is simply the arithmetic average, as is commonly calculated, i.e., x xi , n i1 where i is one of the n measurements of the sample. o We sometimes use the notation xavg instead of x to indicate the average of all x values in the sample, especially when using Excel since overbars are difficult to add.
    [Show full text]
  • ICL8038 TM D FO NDE MME ECO OT R N Data Sheet April 2001 File Number 2864.4
    NS ESIG W D R NE ICL8038 TM D FO NDE MME ECO OT R N Data Sheet April 2001 File Number 2864.4 Precision Waveform Generator/Voltage Features Controlled Oscillator • Low Frequency Drift with Temperature...... 250ppm/oC The ICL8038 waveform generator is a monolithic integrated • LowDistortion...............1%(SineWaveOutput) tle circuit capable of producing high accuracy sine, square, 80 triangular, sawtooth and pulse waveforms with a minimum of • HighLinearity ...........0.1%(Triangle Wave Output) external components. The frequency (or repetition rate) can • Wide Frequency Range ............0.001Hzto300kHz - be selected externally from 0.001Hz to more than 300kHz using either resistors or capacitors, and frequency • VariableDutyCycle.....................2%to98% modulation and sweeping can be accomplished with an • HighLevelOutputs......................TTLto28V ci- external voltage. The ICL8038 is fabricated with advanced • Simultaneous Sine, Square, and Triangle Wave monolithic technology, using Schottky barrier diodes and thin Outputs e- film resistors, and the output is stable over a wide range of temperature and supply variations. These devices may be • Easy to Use - Just a Handful of External Components er- interfaced with phase locked loop circuitry to reduce Required o /Vo temperature drift to less than 250ppm/ C. e - Ordering Information ed PART NUMBER STABILITY TEMP. RANGE (oC) PACKAGE PKG. NO. il- o r) ICL8038CCPD 250ppm/ C(Typ) 0to70 14LdPDIP E14.3 tho ICL8038CCJD 250ppm/oC(Typ) 0to70 14LdCERDIP F14.3 ICL8038BCJD 180ppm/oC(Typ)
    [Show full text]
  • Physics 115A: Statistical Physics
    Physics 115A: Statistical Physics Prof. Clare Yu email: [email protected] phone: 949-824-6216 Office: 210E RH Fall 2013 LECTURE 1 Introduction So far your physics courses have concentrated on what happens to one object or a few objects given an external potential and perhaps the interactions between objects. For example, Newton’s second law F = ma refers to the mass of the object and its acceleration. In quantum mechanics, one starts with Schroedinger’s equation Hψ = Eψ and solves it to find the wavefunction ψ which describes a particle. But if you look around you, the world has more than a few particles and objects. The air you breathe and the coffee you drink has lots and lots of atoms and molecules. Now you might think that if we can describe each atom or molecule with what we know from classical mechanics, quantum mechanics, and electromagnetism, we can just scale up and describe 1023 particles. That’s like saying that if you can cook dinner for 3 people, then just scale up the recipe and feed the world. The reason we can’t just take our solution for the single particle problem and multiply by the number of particles in a liquid or a gas is that the particles interact with one another, i.e., they apply a force on each other. They see the potential produced by other particles. This makes things really complicated. Suppose we have a system of N interacting particles. Using Newton’s equations, we would write: d~p d2~x i = m i = F~ = V (~x , ~x , ..., ~x ) (1) dt dt2 ij −∇ i 1 2 N Xj6=i where F~ij is the force on the ith particle produced by the jth particle.
    [Show full text]
  • Glossary of Transportation Construction Quality Assurance Terms
    TRANSPORTATION RESEARCH Number E-C235 August 2018 Glossary of Transportation Construction Quality Assurance Terms Seventh Edition TRANSPORTATION RESEARCH BOARD 2018 EXECUTIVE COMMITTEE OFFICERS Chair: Katherine F. Turnbull, Executive Associate Director and Research Scientist, Texas A&M Transportation Institute, College Station Vice Chair: Victoria A. Arroyo, Executive Director, Georgetown Climate Center; Assistant Dean, Centers and Institutes; and Professor and Director, Environmental Law Program, Georgetown University Law Center, Washington, D.C. Division Chair for NRC Oversight: Susan Hanson, Distinguished University Professor Emerita, School of Geography, Clark University, Worcester, Massachusetts Executive Director: Neil J. Pedersen, Transportation Research Board TRANSPORTATION RESEARCH BOARD 2017–2018 TECHNICAL ACTIVITIES COUNCIL Chair: Hyun-A C. Park, President, Spy Pond Partners, LLC, Arlington, Massachusetts Technical Activities Director: Ann M. Brach, Transportation Research Board David Ballard, Senior Economist, Gellman Research Associates, Inc., Jenkintown, Pennsylvania, Aviation Group Chair Coco Briseno, Deputy Director, Planning and Modal Programs, California Department of Transportation, Sacramento, State DOT Representative Anne Goodchild, Associate Professor, University of Washington, Seattle, Freight Systems Group Chair George Grimes, CEO Advisor, Patriot Rail Company, Denver, Colorado, Rail Group Chair David Harkey, Director, Highway Safety Research Center, University of North Carolina, Chapel Hill, Safety and Systems
    [Show full text]
  • Chapter 9. Fourier Series A. the Fourier Sine Series
    Vector Spaces in Physics 8/6/2015 Chapter 9. Fourier Series A. The Fourier Sine Series The general solution. In Chapter 8 we found solutions to the wave equation for a string fixed at both ends, of length L, and with wave velocity v, yn x, t A n sin k n x cos n t k n n L 1 n 2L , n = 1, 2, 3, . (9-1) n v n n L v fn n 2L We are now going to proceed to describe an arbitrary motion of the string with both ends fixed in terms of a linear superposition of normal modes: nx general solution, string , (9-2) y x, t Ann sin cos t n1 L fixed at both ends nv where and the coefficients An are to be determined. Here are some things to be noted: n L (1) We are assuming for the moment that this equation is true - that is, in the limit where we include an infinite number of terms, that the infinite series is an arbitrarily good approximation to the solution y x, t . (2) Each term in the series is separately a solution to the wave equation satisfying the boundary conditions, and so the series sum itself is such a solution. (3) This series is sort of like an expansion of a vector in terms of a set of basis vectors. In this picture the coefficients An are the coordinates of the function . (4) We still have to specify initial conditions and find a method to ensure that they are satisfied.
    [Show full text]
  • Power Transmission [120 Marks]
    Power transmission [120 marks] t I 1. The graph shows the variation with time of the current in the primary coil of an ideal transformer. [1 mark] The number of turns in the primary coil is 100 and the number of turns in the secondary coil is 200. Which graph shows the variation with time of the current in the secondary coil? 2. The diagram shows a diode bridge rectification circuit and a load resistor. [1 mark] The input is a sinusoidal signal. Which of the following circuits will produce the most smoothed output signal? The graph shows the power dissipated in a resistor of 100 Ω when connected to an alternating current (ac) power supply of root 3. [1 mark] mean square voltage (Vrms) 60 V. What are the frequency of the ac power supply and the average power dissipated in the resistor? A capacitor consists of two parallel square plates separated by a vacuum. The plates are 2.5 cm × 2.5 cm squares. The capacitance of the capacitor is 4.3 pF. Calculate the distance between the plates. 4a. [1 mark] 4b. The capacitor is connected to a 16 V cell as shown. [2 marks] Calculate the magnitude and the sign of the charge on plate A when the capacitor is fully charged. ε ε 4c. The capacitor is fully charged and the space between the plates is then filled with a dielectric of permittivity = 3.0 0. [2 marks] Explain whether the magnitude of the charge on plate A increases, decreases or stays constant. In a different circuit, a transformer is connected to an alternating current (ac) supply.
    [Show full text]