Reducing Surface Recombination Velocity in Thin Perovskite Films
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Transport of Dangerous Goods
ST/SG/AC.10/1/Rev.16 (Vol.I) Recommendations on the TRANSPORT OF DANGEROUS GOODS Model Regulations Volume I Sixteenth revised edition UNITED NATIONS New York and Geneva, 2009 NOTE The designations employed and the presentation of the material in this publication do not imply the expression of any opinion whatsoever on the part of the Secretariat of the United Nations concerning the legal status of any country, territory, city or area, or of its authorities, or concerning the delimitation of its frontiers or boundaries. ST/SG/AC.10/1/Rev.16 (Vol.I) Copyright © United Nations, 2009 All rights reserved. No part of this publication may, for sales purposes, be reproduced, stored in a retrieval system or transmitted in any form or by any means, electronic, electrostatic, magnetic tape, mechanical, photocopying or otherwise, without prior permission in writing from the United Nations. UNITED NATIONS Sales No. E.09.VIII.2 ISBN 978-92-1-139136-7 (complete set of two volumes) ISSN 1014-5753 Volumes I and II not to be sold separately FOREWORD The Recommendations on the Transport of Dangerous Goods are addressed to governments and to the international organizations concerned with safety in the transport of dangerous goods. The first version, prepared by the United Nations Economic and Social Council's Committee of Experts on the Transport of Dangerous Goods, was published in 1956 (ST/ECA/43-E/CN.2/170). In response to developments in technology and the changing needs of users, they have been regularly amended and updated at succeeding sessions of the Committee of Experts pursuant to Resolution 645 G (XXIII) of 26 April 1957 of the Economic and Social Council and subsequent resolutions. -

Proceedings of the Nuclear Energy Agency International Workshop on Chemical Hazards in Fuel Cycle Facilities Nuclear Processing
Nuclear Safety NEA/ CSNI/R(2019)9/ADD1 May 2019 www.oecd-nea.org Proceedings of the Nuclear Energy Agency International Workshop on Chemical Hazards in Fuel Cycle Facilities Nuclear Processing Appendix C NEA/CSNI/R(2019)9/ADD1 The non-radiological risks involving dangerous chemicals in nuclear fuel cycle facilities - French framework regulation - Youcef HEMIMOU, Brice DELIME, Raffaello AMOROSI, Josquin VERNON French Nuclear Safety Authority 15, rue Louis Lejeune CS70013 – 92541 Montrouge Cedex [email protected] Accidents involving hazardous chemicals pose a significant threat to the population and the environment. Among nuclear facilities, this threat applies in particular to the fuel cycle facilities. As a consequence, the activities related to hazardous chemicals are covered by a legal framework that, depending on the nature of the activity and the associated risks, aims to guarantee that, they will not be likely to be detrimental to safety, public health and environment [1]. The aim of this article is to present a summary of the main regulations involving dangerous chemicals in nuclear fuel cycle facilities that have to be taken into account in the safety demonstration. The latter must prove that the risks of an accident - radiological or not - and the scale of its consequences, given the current state of knowledge, practices and the vulnerability of the installation environment, are as low as possible under acceptable economic conditions. Key words : nuclear fuel cycle facilities, safety demonstration, principle of defence in depth, deterministic approach, probabilistic approach, dangerous chemicals, non-radiological risks, Seveso Directive, domino effects. 1. THE DANGEROUS SUBSTANCES IN NUCLEAR FUEL CYCLE FACILITIES 1.1. -

List of Lists
United States Office of Solid Waste EPA 550-B-10-001 Environmental Protection and Emergency Response May 2010 Agency www.epa.gov/emergencies LIST OF LISTS Consolidated List of Chemicals Subject to the Emergency Planning and Community Right- To-Know Act (EPCRA), Comprehensive Environmental Response, Compensation and Liability Act (CERCLA) and Section 112(r) of the Clean Air Act • EPCRA Section 302 Extremely Hazardous Substances • CERCLA Hazardous Substances • EPCRA Section 313 Toxic Chemicals • CAA 112(r) Regulated Chemicals For Accidental Release Prevention Office of Emergency Management This page intentionally left blank. TABLE OF CONTENTS Page Introduction................................................................................................................................................ i List of Lists – Conslidated List of Chemicals (by CAS #) Subject to the Emergency Planning and Community Right-to-Know Act (EPCRA), Comprehensive Environmental Response, Compensation and Liability Act (CERCLA) and Section 112(r) of the Clean Air Act ................................................. 1 Appendix A: Alphabetical Listing of Consolidated List ..................................................................... A-1 Appendix B: Radionuclides Listed Under CERCLA .......................................................................... B-1 Appendix C: RCRA Waste Streams and Unlisted Hazardous Wastes................................................ C-1 This page intentionally left blank. LIST OF LISTS Consolidated List of Chemicals -
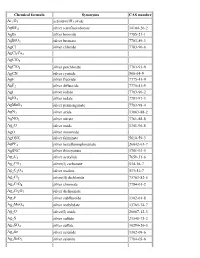
List of Chemical Formulas
Chemical formula Synonyms CAS number Ac2O3 actinium(III) oxide AgBF4 silver tetrafluoroborate 14104-20-2 AgBr silver bromide 7785-23-1 AgBrO3 silver bromate 7783-89-3 AgCl silver chloride 7783-90-6 AgCl3Cu2 AgClO3 AgClO4 silver perchlorate 7783-93-9 AgCN silver cyanide 506-64-9 AgF silver fluoride 7775-41-9 AgF2 silver difluoride 7775-41-9 AgI silver iodide 7783-96-2 AgIO3 silver iodate 7783-97-3 AgMnO4 silver permanganate 7783-98-4 AgN3 silver azide 13863-88-2 AgNO3 silver nitrate 7761-88-8 Ag2O silver oxide 1301-96-8 AgO silver monoxide AgONC silver fulminate 5610-59-3 AgPF6 silver hexafluorophosphate 26042-63-7 AgSNC silver thiocyanate 1701-93-5 Ag2C2 silver acetylide 7659-31-6 Ag2CO3 silver(I) carbonate 534-16-7 Ag2C2O4 silver oxalate 533-51-7 Ag2Cl2 silver(II) dichloride 75763-82-5 Ag2CrO4 silver chromate 7784-01-2 Ag2Cr2O7 silver dichromate Ag2F silver subfluoride 1302-01-8 Ag2MoO4 silver molybdate 13765-74-7 Ag2O silver(I) oxide 20667-12-3 Ag2S silver sulfide 21548-73-2 Ag2SO4 silver sulfate 10294-26-5 Ag2Se silver selenide 1302-09-6 Ag2SeO3 silver selenite 7784-05-6 Ag2SeO4 silver selenate 7784-07-8 Ag2Te silver(I) telluride 12002-99-2 Ag3Br2 silver dibromide 11078-32-3 Ag3Br3 silver tribromide 11078-33-4 Ag3Cl3 silver(III) trichloride 12444-96-1 Ag3I3 silver(III) triiodide 37375-12-5 Ag3PO4 silver phosphate 7784-09-0 AlBO aluminium boron oxide 12041-48-4 AlBO2 aluminium borate 61279-70-7 AlBr aluminium monobromide 22359-97-3 AlBr3 aluminium tribromide 7727-15-3 AlCl aluminium monochloride 13595-81-8 AlClF aluminium chloride fluoride -

"Noble-Gas Chemistry and the Periodic System of Mendeleev" By
"Noble-Gas Chemistry and The Periodic System of Mendeleev" By Neil Bartlett Materials and Molecular Research Division, Lawrence Berkeley Laboratory and Department of Chemistry, University of California Berkeley, California U.S.A. The Stable Noble-Gas Electron Configuration When, in 1962, chemists were informed that a compound of a noble- gas had been prepared', there was much expression of surprise and ini- tially even disbelief. Faith in the chemical inertness of the noble gases had been fostered in part by previous failures to prepare compounds. The greatest prejudice, however, derived from the electronic theories of the chemical bond, which stressed the noble-gas electron arrangement as the ideal to which all other atoms tended. When the noble gases were discovered2, in the last years of the 19th Century, they were quickly recognized as a new Group of elements of Mende- * leev's Table of The Elements. This new Group of elements fitted naturally into the "Table", each noble-gas being located .between a halogen and an alkali metal. Since the Halogens included the most strongly oxidizing elements, whereas the Alkali Metals were the most strongly reducing ele- ments of the Periodic Table, it was appropriate, for the intervening group of elements, to exhibit neither oxidizing nor reducing properties, i.e. to be chemically unreactive. All efforts to oxidize or reduce helium and argon' (i.e. to bring them into chemical combination with other elements) failed!, perhaps the most significant failure being Moissan's attempt in 1895 to prepare an argon fluoride3. The rarer noble gases were not sub- jected to the same intensive chemical investigation, and no claim for chemical activity of the gases was sustained prior to 1962. -

Lawrence Berkeley National Laboratory Recent Work
Lawrence Berkeley National Laboratory Recent Work Title NOBLE-GAS CHEMISTRY AND ITS SIGNIFICANCE. Permalink https://escholarship.org/uc/item/2dx0900q Author Bartlett, Neil. Publication Date 1971-11-01 eScholarship.org Powered by the California Digital Library University of California Presented as the Dannie-Heineman .. .. LBL-416 ~ Prize Address, Gottingen, Germany Preprint c. November 26, 1971 D'JCU:ViENYS SE. ij(, ~ NOBLE -GAS CHEMISTRY AND ITS SIGNIFICANCE Neil Bartlett November 1971 AEC Contract No. W -7405-eng-48 TWO-WEEK lOAN COPY This is a Library Circulating Copy which may be borrowed for two weeks. For a personal retention copy, call Tech. Info. Dioision, Ext. 5545 DISCLAIMER This document was prepared as an account of work sponsored by the United States Government. While this document is believed to contain correct information, neither the United States Government nor any agency thereof, nor the Regents of the University of California, nor any of their employees, makes any warranty, express or implied, or assumes any legal responsibility for the accuracy, completeness, or usefulness of any information, apparatus, product, or process disclosed, or represents that its use would not infringe privately owned rights. Reference herein to any specific commercial product, process, or service by its trade name, trademark, manufacturer, or otherwise, does not necessarily constitute or imply its endorsement, recommendation, or favoring by the United States Government or any agency thereof, or the Regents of the University of California. The views and opinions of authors expressed herein do not necessarily state ·or reflect those of the United States Government or any agency thereof or the Regents of the University of California. -

Summaries of the Usaec Basic Research Program in Chemistry (On Site )
TID-4005(Pt. 2b) SUMMARIES OF THE USAEC BASIC RESEARCH PROGRAM IN CHEMISTRY (ON SITE ) August 1964 Division of Research, AEC UNITED STATES ATOMIC ENERGY COMMISSION Division of Technical Information LEGAL NOTICE This report was prepared as an account of Government sponsored work. Neither the United States, nor the Commission, nor any person acting on behalf of the Commission: A. Makes any warranty or representation, expressed or implied, with respect to the accu- racy, completeness, or usefulness of the information contained in this report, or that the use of any information, apparatus, method, or process disclosed in this report may not infringe privately owned rights; or B. Assumes any liabilities with respect to the use of, or for damages resulting from the use of any information, apparatus, method, or process disclosed in this report. As used in the above, "person acting on behalf of the Commission" includes any em- ployee or contractor of the Commission, or employee of such contractor, to the extent that such employee or contractor of the Commission, or employee of such contractor prepares, disseminates, or provides access to, any information pursuant to his employment or contract with the Commission, or his employment with such contractor. This report has been reproduced directly from the best available copy. Printed in USA. Price $7.90. Available from the Clearing- house for Federal Scientific and Technical Information, Na- tional Bureau of Standards, U. S. Department of Commerce, Springfield, Va. USltCOiritlen ofInt-itsl Infenwiio(»«»;(» Ook ll~.df T»wu- TID - 4005(Pt. 2b) CHEMISTRY (TID-4500, 33rd. Ed.) SUMMARIES OF THE USAEC BASIC RESEARCH PROGRAM IN CHEMISTRY (On Site) Division of Research, AEC Indexes prepared by Division of Technical Information Extension August 1964 UNITED STATES ATOMIC ENERGY COMMISSION Division of Technical Information FOREWORD The Atomic Energy Act directs the Atomic Energy Commission to support and foster research in the field of atomic energy. -

Technical Report for the Substantial Modification Rule for 62-730, F.A.C
Technical Report for the Substantial Modification Rule for 62-730, F.A.C. Prepared for the Hazardous Waste Regulation Section Florida Department of Environmental Protection By Kendra F. Goff, Ph. D. Stephen M. Roberts, Ph.D. Center for Environmental & Human Toxicology University of Florida Gainesville, Florida August 1, 2008 During an adverse event, such as a fire or explosion, hazardous materials from a storage or transfer facility may be released into the atmosphere. The potential human health impacts of such a release are assessed through air modeling coupled with chemical-specific inhalation criteria for short-term exposures. With this approach, distances from the facility over which differing levels of health effects from inhalation of airborne hazardous materials are expected can be predicted. Because the movement in air and toxic potency varies among chemicals, the potential impact area for a facility is dependent upon the chemicals present and their quantities. The impact area can be calculated for a facility under current and possible future conditions. This information can be used to determine whether proposed changes in storage conditions or the nature and quantities of chemicals handled would result in a substantial difference in the area of potential impact. The following sections provide technical guidance on how impact areas for facilities handling hazardous materials under Chapter 62-730, F.A.C. should be determined. Air modeling. Any model used for the purposes of demonstration must be capable of producing results in accordance with worst-case scenario provisions of Program 3 of the Accidental Release Prevention Program of s. 112(r)(7) of the Clean Air Act. -

J. Amer. Chem. Soc., 1958, 80, 4466
1st NORANDA LECTURE Unusual Oxidation States of the Noble Elements NEIL BARTLETT, M.C.I.C., pentafluoride may be preparable although the thermal University of British Columbia, stability may be low. A higher fluoride of ruthenium than Vancouver, B.C. the hexafluoride appears to be unlikely in view of the thermal instability of this fluoride. ITHl the past six years the fluorine chemistry of the The data for the second and third transition series hexa W noble metals has been revised and considerably ex fluorides given in Table 3, show the fusion point and tended. Weinstock and his co-workers at the Argonne boiling point rising with increasing atomic number along ational Laboratory have contributed significantly to the each series as the effective molecular volume decreases. changes (1) . They have reported four new hexafluorides These trends indicate a significant increase in the inter <2 ( 3 ), 4 ), <5)) 6 ) (PtF,; l, TcF6 RuFG( RhF0 and have shown ( molecular attraction with atomic number in each series. the fluoride previously considered to be osmium octa Thermal stability falls with atomic number in each series fluoride to be the hexafluoride. In addition, rhenium hepta also and there is apparently a correlation between thermal fluoride has been prepared and characterized <7 ). stability and effective molecular volume, platinum hexa The known highest oxides· and !}uorides of the second fluoride being comparable, in stability and molecular and third transition series elements are listed in Table 1. volume, with ruthenium hexafluoride, and rhodium hexa An interesting feature of this comparison is that although fluoride with the smallest molecular volume being the least rhodium hexafluoride exists the trioxide is unknown, but thermally stable hexafluoride and the most difficult one to the highest fluoride of ruthenium is· the hexafluoride despite make. -

Download The
The University of British Columbia FACULTY OF GRADUATE STUDIES PROGRAMME OF THE FINAL ORAL EXAMINATION FOR THE DEGREE OF DOCTOR OF PHILOSOPHY of NARENDRA KUMAR JHA B,Sc (Hons.)j Patna University/India 1955 M.Sc, Patna University, India 1957 TUESDAY, SEPTEMBER 28, 1965 AT 10;00 A.M. IN ROOM 2633 CHEMISTRY BUILDING COMMITTEE IN CHARGE Chairmano M. Darrach. N. Bart Lett R, C= Thompson C. A, McDowell R. M, Thompson C Reid J. Trotter External Examiner; R. D. Peacock Department of Chemistry The University of Birmingham Birmingham 15? England THE FLUORIDES AND OXYFLUORIDES OF OSMIUM AND THE OXIDIZING PROPERTIES OF THE NOBLE METAL HEXAFLUORIDES ABSTRACT An investigation of the attainable oxidation states of osmium in reaction with fluorine and fluorine-oxygen mixtures was carried out. The first simple heptavalent compound of osmium, osmium oxide pentafluoride, OsOf^, was prepared by the fluorination of anhydrous osmium dioxide. This compound was characterized by analysis. X-ray single crystal and powder methods, and by infrared spectroscopy. The vapour pressure-temperature relationship and derived thermodynamic data have been evaluated^ The magnetic susceptibility has been measured over the temperature range 77° to 300°K. The existence of an octavalent osmium oxyfluoride, osmium trioxide difluoride, OSO3F2 has been confirmed. This compound is diamagnetic and the solid is dimorphic. Preliminary structural work has indicated that the osmium is six- coordinated in this compound. A related ternary fluoride, NOOSO3F3 containing octavalent osmium was prepared and characterized. The results of the investigations indicate that OSO2F4 and higher fluorides of osmium than 0sF6 are unlikely to be stable at ordinary temperatures and pressures. -

Vapor Pressure 6-60
VAPOR PRESSURE This table gives vapor pressure data for about 1800 inorganic and organic substances. In order to accommodate elements and compounds ranging from refractory to highly volatile in a single table, the temperature at which the vapor pressure reaches specified pressure values is listed. The pressure values run in decade steps from 1 Pa (about 7.5 µm Hg) to 100 kPa (about 750 mm Hg). All temperatures are given in °C. The data used in preparing the table came from a large number of sources; the main references used for each substance are indicated in the last column. Since the data were refit in most cases, values appearing in this table may not be identical with values in the source cited. The temperature entry in the 100 kPa column is close to, but not identical with, the normal boiling point (which is defined as the temperature at which the vapor pressure reaches 101.325 kPa). Although some temperatures are quoted to 0.1°C, uncertainties of several degrees should generally be assumed. Values followed by an “e” were obtained by extrapolating (usually with an Antoine equation) beyond the region for which experimental measurements were available and are thus subject to even greater uncertainty. Compounds are listed by molecular formula following the Hill convention. Substances not containing carbon are listed first, followed by those that contain carbon. To locate an organic compound by name or CAS Registry Number when the molecular formula is not known, use the table Physical Constants of Organic Compounds in Section 3 and its indexes to determine the molecular formula. -

Aug. 21, 1973 3,753,920
Aug. 21, 1973 L. J.ANASTASIA ETAL 3,753,920 FLUORIDE REPROCESSING OF BREEDER FUELS Original Filed Oct. 24, 1968 2 Sheets-Sheet 1 Aug. 21, 1973 L. J. ANASTASIA ET AL 3,753,920 FLUORIDE REPROCESSING OF BREEDER FUELS 2 Sheets-Sheet 3 Original Filed Oct. 24, 1968 1 1 I, £ 1 M fcl it O Lk N C* Uj vn el 3,753,920 United States Patent Office Patented Aug. 21, 1973 erate large quantities of plutonium while at the same time 3 753 920 producing power. It is necessary to reprocess spent breeder FLUORIDE REPROCESSING OF BREEDER FUELS fuel to separate the uranium and plutonium from fission Louis J. Anastasia, Midlothian, Erwin L. Carls, Glen products produced during irradiation. New processes are Ellyn, Albert A. Chilenskas, Chicago, Johan E. A. g necessary for handling the new breeder fuels. Graae, and Albert A. Jonke, Elmhurst, Norman M. A fluoride volatility process has been developed at Levitz, Bellwood, Martin J. Steindler, Park Forest, and La Verne E. Trevorrow, Glen Ellyn, HI., assignors Argonne National Laboratory for continuously reprocess- to the United States of America as represented by the ing spent breeder fuels. The object of this invention is to United States Atomic Energy Commission reprocess spent oxide fuel to produce either plutonium Continuation of abandoned application Ser. No. 770,145, 10 dioxide and uranium dioxide separately or a mixed prod- Oct. 24, 1968. This application Aug. 12, 1971, Ser. uct of 23% plutonium dioxide-uranium dioxide with a No. 171,315 fission product decontamination factor of 106 to 107.