DOCSLIB.ORG

Vaccination and Herd Immunity to Infectious Diseases Roy M

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Vaccination and Herd Immunity to Infectious Diseases Roy M _NA'-"TU-'---'-'R-"E'--V-'---O'-'-L.-'3_1.c...8.c.2.c...8c...N--'.O_V.=EM'-'-"-BECCR'-'----'-l'---'98'-'--5-------REVIEW ARTICLE-------------------3~23 Vaccination and herd immunity to infectious diseases Roy M. Anderson & Robert M. May· Department of Pure and Applied Biology, Imperial College, London University, London SW7 2BB, UK * Biology Department, Princeton University, Princeton, New Jersey 08540, USA An understanding of the relationship between the transmission dynamics of infectious agents and herd immunity provides a template for the design of effective control programmes based on mass immuniz­ ation. Mathematical models of the spread and persistence of infection provide important insights into the problem of how best to protect the community against disease. MUCH attention is now focused on the development and com­ of acquired immunity and maternally derived protection, age­ munity-wide use of vaccines for the control of infectious dis­ related changes in the degree and intimacy of contacts among eases. This interest is a consequence of many factors; these people, and the prevailing levels of genetic, spatial and include the worldwide eradication of smallpox by vaccination behavioural heterogeneity in susceptibility/resistance to infec­ in the late 1970s1, the current success of child immunization tion. Intuition built on many years of practical epidemiological programmes for the control of measles, mumps, pertussis and experience often fails to predict the outcome of a particular rubella in the United States2·3, the failure of frequent appeals vaccination programme. Mathematical models which clearly by public health authorities in the United Kingdom to raise and accurately define the details of the association between vaccination rates that are at present low by developed-country disease agent and host (at the individual and population levels) 4 standards ·', the Expanded Programme on Immunization (EPI) can help to overcome such difficulties. This article reviews recent of the World Health Organisation (WHO) for the control of a theoretical and empirical work on the transmission dynamics variety of serious childhood viral and bacterial diseases in the of infectious disease. Emphasis is placed on the relevance of 8 12 developing world • , and the rapid advances in molecular bio­ such research to the design of disease control programmes based logy and biotechnology which promise new vaccines for the on vaccination. 13 16 future - • The main thrust of research today is at the molecular level, where it is stimulated by the urgent need to develop General theory vaccines for the major killing diseases of the Third World such Models for the transmission dynamics of directly transmitted 11 1 as malaria • 9, and to combat new infections such as the current viral and bacterial infections are typically compartmental in 23 35 epidemic of AIDS (acquired immune deficiency syndrome), structure · • They represent changes, with respect to age, a, caused by the recently isolated human T-lymphotropic virus and time, I, in the populations of infants protected by maternally 20 21 (HTL V-III) • • derived antibodies (M(a, t)), susceptible individuals (X(a, 1)), The development of a safe, effective and cheap vaccine, infected individuals who are not yet infectious (H(a, t)), infec­ however, is only a first step (albeit an essential one) towards tious people ( Y(a, t)), and people who have recovered and are community-wide control. Epidemiological, economic and moti­ immune from subsequent infection (Z,(a, t)). The total popula­ vational issues are at least as important as technological ones. tion is N(a, 1) = M(a, t) + X(a, t) + H(a, t) + Y(a, t) + Z(a, t). 12 A vaccine for measles (a very cost-effective immunization ) has The deterministic equations describing the flows from one class 24 25 27 been available since the late 1960s, yet the infection remains to another are of the general form • • 8 22 one of the world's major causes of child mortality • • Concomi­ aM(a, 1) aM(a, t) tant with research on vaccine development, there is a need for ---+--- -[µ(a)+d]M(a, t) an improved understanding ofhow best to use vaccines to protect at aa the community as well as the individual. The persistence of aX(a, t) aX(a, t) infectious disease within a population requires the density of ---+--- dM(a, t) susceptible individuals to exceed a critical value such that, on at aa average, each primary case of infection generates at least one -[v(a, t)+A(a, t)+ µ(a)]X(a, t) secondary case. It is therefore not necessary to vaccinate every­ aH(a, 1) aH(a, t) one within a community to eliminate infection; the level of herd ---+--- A(a, t) X(a, t) immunity must simply be sufficient to reduce the susceptible at aa fraction below the critical point. The central epidemiological -[µ(a)+a]H(a, 1) (1) questions are thus: what proportion of the population should be vaccinated to achieve elimination (in a local programme), a Y(a, t) a Y(a, t) ---+--- aH(a, t)-[µ(a)+y]Y(a, 1) eradication (in a global programme) or a defined level of con­ a1 aa trol? How is this affected by demographic factors (for example, az(a, 1) aZ(a, 1) birth rate)? What is the best age at which to immunize? How ---+---= yY(a, t)+ v(a, t) X(a, t) does mass immunization affect the age distribution of susceptible at aa individuals, particularly in those classes most at risk from serious -µ(a) Z(a, t) disease, and how important is genetic and spatial heterogeneity in suceptibility to infection (or response to immunization) to aN(a, t) aN(a, t) 23 26 ---+--- -µ(a) N(a, 1) the creation of effective herd immunity • ? a, aa To answer these questions, we need to understand the interac­ tion between the transmission dynamics of the disease agent Here µ(a) denotes age-related human mortality, 1/d is the and the level of naturally acquired (or artificially created) average duration of protection provided by maternal antibodies, immunity to infection. This relationship is complex and depends 1/ a and 1/ y are the average incubation and infectious periods on such factors as the precise course of infection within an respectively, and v( a, t) records the age- and time-specific individual, the demography of the host population, the duration vaccination schedule. Mortality explicitly associated with the © 1985 Nature Publishing Group 3_24_____________________ REVIEWARTICLE---------~N~A.c..cTUc...c..c.RE=-V-O'-'L'--.-'-3_18_2C-'8-'-N'--O'--V_E=MB~E=R'--1=9~85 Fig. 1 a, Time series analysis of the case so,ooo a resports for measles in England and Wales over the pre-vaccination period 1948-68. The top ~ 4 O, 0 0 0 e graph denotes the recorded cases and the bottom ; c 1.4 ~--------------, st 8 b graph the serial corrclogram • Note the sig- ~ 30,000 ., 1.2 nificant yearly (seasonal) and 2-yearly peaks in a. 0 incidence (the horizontal axis in the bottom "' 20,000 .; graph denotes weeks). b, Model predictions of 5 e the equilibrium (the state to which the system u 10,000 .! 0.8 .; settles in the long term) ratio of the number of 0.6 cases of mumps in the age range 14-50 yr (the ., 1953 1958 1963 1968 "' age range in which males are at risk to serious = 0.4 Year u disease resulting from infection) under the C 1.0 0.2 impact of a vaccination programme in which p .!2 o iii of each yearly cohort arc vaccinated at age 2 yr, 0.5 ~ 0.2 0.4 0.6 0.8 divided by the number of cases in the same age 0 0.0 range before vaccination. If the ratio is above u Proportion vaccinated unity, the control programme has a deterimental ~ -0.5 <( effect and vice versa. The average age at infection -1.0 Time lag <weeks) before control was assumed to be 6.5 yr e d (appropriate for the United Kingdom) and the c calculations were based on a model defined in g 2 ,----------------, 0 ref. 24. The straight line denotes the ratio of ~ 1.8 C " unity. c, Age-specific incidence of reported ~ ., ,_ 6 measles encephalitis cases ( defined per 1,000 a. ., 1 4 cases of measles) in the United States in 1973- :i ~ · 116 1 2 79 • d, Similar to b but representing the ratio ,. ~ · of cases after vaccination divided by cases before u 1. 0 O vaccination for rubella in the United Kingdom ~ ., 0. 8 in the age range 16-40 yr. The graph denotes .; ~ o.6 model predictions (equilibrium values) for a -a ~ o.• two-stage vaccination policy involving vaccina· _ g 0 2 tion of only girls at age 12 yr (the UK policy) w and vaccination of boys and girls at age 2 yr (the 0 2 10 12 14 16 18 20 25 67 US policy ) • • Note that the addition of a Age <yr) second-stage US policy over the current UK policy is only of substantial benefit if moderate to high levels of vaccination coverage are achieved at 2 yr of age. The average age at infection before control was 25 67 assumed to be 9-10 yr of age • . infection has been ignored. The term A(a, t) denotes the 'force' unity. Within communities in which the infection is endemic, 23 37 or rate of infection, which under the 'mass action' assumption ~ is inversely correlated with A, the average age at infection - 24 30 adopts the form - A(a, t) = J~f3(a, a') Y(a', t) da'. Here (~= B/(A- D)). This relation holds both for developed coun­ {3(a, a') represents the transmission coefficient for infected tries (growth rates essentially zero) and for developing countries individuals in age class a' who come into contact with suscep­ (with their growing populations)52 .
Load more

Recommended publications
  • Vaccination Certificate Information Version: 21 July 2021
    معلومات عن شهادة التطعيم، بالعربية 中文疫苗接种凭证信息 Informations sur le certificat de vaccination en FRANÇAIS Информация о сертификате вакцинации на РУССКОМ ЯЗЫКЕ Información sobre el Certificado de Vacunación en ESPAÑOL UN SYSTEM-WIDE COVID-19 VACCINATION PROGRAMME VACCINATION CERTIFICATE INFORMATION VERSION: 21 JULY 2021 ABOUT THE UN SYSTEM-WIDE COVID-19 VACCINATION PROGRAMME The UN is committed to ensuring the protection of its personnel. Tasked by the Secretary-General, the Department of Operational Support (DOS) is leading a coordinated, UN-system-wide effort to ensure the availability of vaccine to UN personnel, their dependents and implementing partners. The roll-out of the UN System-wide COVID-19 Vaccination Programme (the “Programme”) for UN personnel will provide a significant boost to the ability of personnel to stay and deliver on the Organization's mandates, to support beneficiaries in the communities they serve, and to contribute to our on-going work to recover better together from the pandemic. Information about the Programme is available at: https://www.un.org/en/coronavirus/vaccination ABOUT THE VACCINATION CERTIFICATE Upon administration of the requisite vaccine dosage, a certificate of vaccination is generated through the Programme’s registration platform (the “Platform”). The certificate generated by the Platform uses a standardized format, similar to the one used by the WHO in its “International Certificate of Vaccination or Prophylaxis” (Yellow) vaccination booklet. Note: This certificate may not dispense with travel restrictions put in place by the country(ies) of destination. As the nature of the pandemic continues to rapidly evolve, it is highly advisable to check the latest travel regulations.
    [Show full text]
  • Global Dynamics of a Vaccination Model for Infectious Diseases with Asymptomatic Carriers
    MATHEMATICAL BIOSCIENCES doi:10.3934/mbe.2016019 AND ENGINEERING Volume 13, Number 4, August 2016 pp. 813{840 GLOBAL DYNAMICS OF A VACCINATION MODEL FOR INFECTIOUS DISEASES WITH ASYMPTOMATIC CARRIERS Martin Luther Mann Manyombe1;2 and Joseph Mbang1;2 Department of Mathematics, Faculty of Science University of Yaounde 1, P.O. Box 812 Yaounde, Cameroon 1;2;3; Jean Lubuma and Berge Tsanou ∗ Department of Mathematics and Applied Mathematics University of Pretoria, Pretoria 0002, South Africa (Communicated by Abba Gumel) Abstract. In this paper, an epidemic model is investigated for infectious dis- eases that can be transmitted through both the infectious individuals and the asymptomatic carriers (i.e., infected individuals who are contagious but do not show any disease symptoms). We propose a dose-structured vaccination model with multiple transmission pathways. Based on the range of the explic- itly computed basic reproduction number, we prove the global stability of the disease-free when this threshold number is less or equal to the unity. Moreover, whenever it is greater than one, the existence of the unique endemic equilibrium is shown and its global stability is established for the case where the changes of displaying the disease symptoms are independent of the vulnerable classes. Further, the model is shown to exhibit a transcritical bifurcation with the unit basic reproduction number being the bifurcation parameter. The impacts of the asymptomatic carriers and the effectiveness of vaccination on the disease transmission are discussed through through the local and the global sensitivity analyses of the basic reproduction number. Finally, a case study of hepatitis B virus disease (HBV) is considered, with the numerical simulations presented to support the analytical results.
    [Show full text]
  • The Uncertainties Underlying Herd Immunity Against COVID-19
    Preprints (www.preprints.org) | NOT PEER-REVIEWED | Posted: 8 July 2020 doi:10.20944/preprints202007.0159.v1 Communication The uncertainties underlying herd immunity against COVID-19 Farid Rahimi1*and Amin Talebi Bezmin Abadi2* 1 Research School of Biology, The Australian National University, Canberra, Australia; [email protected] 2 Department of Bacteriology, Faculty of Medical Sciences, Tarbiat Modares University, Tehran, Iran; Amin [email protected] * Correspondence: [email protected]; Tel.: +61-2-6125-2851 (F.R.); [email protected]; Tel.: +98-8288-4883 (A.T.B.A.) Abstract: Herd immunity happens when a relatively large proportion of a population becomes infected by an agent, subsequently recovers, and attains immunity against the same agent. That proportion thus indirectly protects the naïve population by preventing the spread of the infection. Herd immunity has been suggested to interrupt and control the COVID-19 pandemic. However, relying on establishing herd immunity can be catastrophic considering the virulence and lethality of SARS-CoV-2. Meanwhile our understanding of the pathogenesis, case-fatality rate, transmission routes, and antiviral therapy for COVID-19 remains limited now. Interrupting or slowing the COVID-19 transmission seems more opportune than vaccination, antiviral therapy, or herd immunity, all of which will take some time to yield. Thus, social distancing, face-masking, and hygiene are the most appropriate immediate countermeasures. Because the social fabrics, economic implications, and local demands of various nations are unique, early relaxation of restrictions may seem hasty particularly when fatality rates are high, or when the healthcare systems could be inadequate or become inundated.
    [Show full text]
  • Vaccine Hesitancy
    WHY CHILDREN WORKSHOP ON IMMUNIZATIONS ARE NOT VACCINATED? VACCINE HESITANCY José Esparza MD, PhD - Adjunct Professor, Institute of Human Virology, University of Maryland School of Medicine, Baltimore, MD, USA - Robert Koch Fellow, Robert Koch Institute, Berlin, Germany - Senior Advisor, Global Virus Network, Baltimore, MD, USA. Formerly: - Bill & Melinda Gates Foundation, Seattle, WA, USA - World Health Organization, Geneva, Switzerland The value of vaccination “The impact of vaccination on the health of the world’s people is hard to exaggerate. With the exception of safe water, no other modality has had such a major effect on mortality reduction and population growth” Stanley Plotkin (2013) VACCINES VAILABLE TO PROTECT AGAINST MORE DISEASES (US) BASIC VACCINES RECOMMENDED BY WHO For all: BCG, hepatitis B, polio, DTP, Hib, Pneumococcal (conjugated), rotavirus, measles, rubella, HPV. For certain regions: Japanese encephalitis, yellow fever, tick-borne encephalitis. For some high-risk populations: typhoid, cholera, meningococcal, hepatitis A, rabies. For certain immunization programs: mumps, influenza Vaccines save millions of lives annually, worldwide WHAT THE WORLD HAS ACHIEVED: 40 YEARS OF INCREASING REACH OF BASIC VACCINES “Bill Gates Chart” 17 M GAVI 5.6 M 4.2 M Today (ca 2015): <5% of children in GAVI countries fully immunised with the 11 WHO- recommended vaccines Seth Berkley (GAVI) The goal: 50% of children in GAVI countries fully immunised by 2020 Seth Berkley (GAVI) The current world immunization efforts are achieving: • Equity between high and low-income countries • Bringing the power of vaccines to even the world’s poorest countries • Reducing morbidity and mortality in developing countries • Eliminating and eradicating disease WHY CHILDREN ARE NOT VACCINATED? •Vaccines are not available •Deficient health care systems •Poverty •Vaccine hesitancy (reticencia a la vacunacion) VACCINE HESITANCE: WHO DEFINITION “Vaccine hesitancy refers to delay in acceptance or refusal of vaccines despite availability of vaccination services.
    [Show full text]
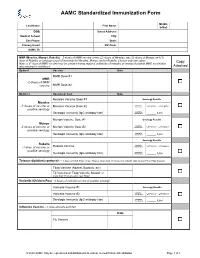
  • AAMC Standardized Immunization Form
    AAMC Standardized Immunization Form Middle Last Name: First Name: Initial: DOB: Street Address: Medical School: City: Cell Phone: State: Primary Email: ZIP Code: AAMC ID: MMR (Measles, Mumps, Rubella) – 2 doses of MMR vaccine or two (2) doses of Measles, two (2) doses of Mumps and (1) dose of Rubella; or serologic proof of immunity for Measles, Mumps and/or Rubella. Choose only one option. Copy Note: a 3rd dose of MMR vaccine may be advised during regional outbreaks of measles or mumps if original MMR vaccination was received in childhood. Attached Option1 Vaccine Date MMR Dose #1 MMR -2 doses of MMR vaccine MMR Dose #2 Option 2 Vaccine or Test Date Measles Vaccine Dose #1 Serology Results Measles Qualitative -2 doses of vaccine or Measles Vaccine Dose #2 Titer Results: Positive Negative positive serology Quantitative Serologic Immunity (IgG antibody titer) Titer Results: _____ IU/ml Mumps Vaccine Dose #1 Serology Results Mumps Qualitative -2 doses of vaccine or Mumps Vaccine Dose #2 Titer Results: Positive Negative positive serology Quantitative Serologic Immunity (IgG antibody titer) Titer Results: _____ IU/ml Serology Results Rubella Qualitative Positive Negative -1 dose of vaccine or Rubella Vaccine Titer Results: positive serology Quantitative Serologic Immunity (IgG antibody titer) Titer Results: _____ IU/ml Tetanus-diphtheria-pertussis – 1 dose of adult Tdap; if last Tdap is more than 10 years old, provide date of last Td or Tdap booster Tdap Vaccine (Adacel, Boostrix, etc) Td Vaccine or Tdap Vaccine booster (if more than 10 years since last Tdap) Varicella (Chicken Pox) - 2 doses of varicella vaccine or positive serology Varicella Vaccine #1 Serology Results Qualitative Varicella Vaccine #2 Titer Results: Positive Negative Serologic Immunity (IgG antibody titer) Quantitative Titer Results: _____ IU/ml Influenza Vaccine --1 dose annually each fall Date Flu Vaccine © 2020 AAMC.
    [Show full text]
  • Herd Immunity Is an Important—And Often Misunderstood—Public Health Phenomenon
    CORE CONCEPTS Herd immunity is an important—and often misunderstood—public health phenomenon CORE CONCEPTS Amy McDermott, Science Writer In December, Anthony Fauci predicted that 70 to 85% Since the earliest months of the COVID-19 pan- of the United States population may need to be demic, “herd immunity” has become shorthand for vaccinated to achieve “herd immunity” against SARS- the day when enough people are immune to the virus CoV-2 (1). Yet he was very careful to qualify his com- that social distancing can end and healthcare systems ments. “We need to have some humility here,” he said are no longer overwhelmed. People have been clam- ’ in a New York Times interview, “We really don’t know oring to know when we ll get there. But even as Fauci — what the real number is.” (2) Fauci, director of the and other officials continue to try to calculate and communicate—when it might happen, they have to National Institute of Allergy and Infectious Diseases, contend with both public misunderstanding of the admitted that the number could be as high as 90%. term and scientific disagreement over what it means. But even a year into the pandemic, there were too The public health concept of herd immunity has a many uncertainties to offer a definite threshold. And more nuanced definition than its popular usage, which with vaccine hesitancy widespread, he worried that is one reason why predicting when we’ll achieve it re- setting the bar at such a high number would cause mains difficult. In theory, estimating the threshold to the public to despair of ever reaching it.
    [Show full text]
  • Using Proper Mean Generation Intervals in Modeling of COVID-19
    ORIGINAL RESEARCH published: 05 July 2021 doi: 10.3389/fpubh.2021.691262 Using Proper Mean Generation Intervals in Modeling of COVID-19 Xiujuan Tang 1, Salihu S. Musa 2,3, Shi Zhao 4,5, Shujiang Mei 1 and Daihai He 2* 1 Shenzhen Center for Disease Control and Prevention, Shenzhen, China, 2 Department of Applied Mathematics, The Hong Kong Polytechnic University, Hong Kong, China, 3 Department of Mathematics, Kano University of Science and Technology, Wudil, Nigeria, 4 The Jockey Club School of Public Health and Primary Care, Chinese University of Hong Kong, Hong Kong, China, 5 Shenzhen Research Institute of Chinese University of Hong Kong, Shenzhen, China In susceptible–exposed–infectious–recovered (SEIR) epidemic models, with the exponentially distributed duration of exposed/infectious statuses, the mean generation interval (GI, time lag between infections of a primary case and its secondary case) equals the mean latent period (LP) plus the mean infectious period (IP). It was widely reported that the GI for COVID-19 is as short as 5 days. However, many works in top journals used longer LP or IP with the sum (i.e., GI), e.g., >7 days. This discrepancy will lead to overestimated basic reproductive number and exaggerated expectation of Edited by: infection attack rate (AR) and control efficacy. We argue that it is important to use Reza Lashgari, suitable epidemiological parameter values for proper estimation/prediction. Furthermore, Institute for Research in Fundamental we propose an epidemic model to assess the transmission dynamics of COVID-19 Sciences, Iran for Belgium, Israel, and the United Arab Emirates (UAE).
    [Show full text]
  • Statements Contained in This Release As the Result of New Information Or Future Events Or Developments
    Pfizer and BioNTech Provide Update on Booster Program in Light of the Delta-Variant NEW YORK and MAINZ, GERMANY, July 8, 2021 — As part of Pfizer’s and BioNTech’s continued efforts to stay ahead of the virus causing COVID-19 and circulating mutations, the companies are providing an update on their comprehensive booster strategy. Pfizer and BioNTech have seen encouraging data in the ongoing booster trial of a third dose of the current BNT162b2 vaccine. Initial data from the study demonstrate that a booster dose given 6 months after the second dose has a consistent tolerability profile while eliciting high neutralization titers against the wild type and the Beta variant, which are 5 to 10 times higher than after two primary doses. The companies expect to publish more definitive data soon as well as in a peer-reviewed journal and plan to submit the data to the FDA, EMA and other regulatory authorities in the coming weeks. In addition, data from a recent Nature paper demonstrate that immune sera obtained shortly after dose 2 of the primary two dose series of BNT162b2 have strong neutralization titers against the Delta variant (B.1.617.2 lineage) in laboratory tests. The companies anticipate that a third dose will boost those antibody titers even higher, similar to how the third dose performs for the Beta variant (B.1.351). Pfizer and BioNTech are conducting preclinical and clinical tests to confirm this hypothesis. While Pfizer and BioNTech believe a third dose of BNT162b2 has the potential to preserve the highest levels of protective efficacy against all currently known variants including Delta, the companies are remaining vigilant and are developing an updated version of the Pfizer-BioNTech COVID-19 vaccine that targets the full spike protein of the Delta variant.
    [Show full text]
  • COVID-19 Vaccines Frequently Asked Questions
    Page 1 of 12 COVID-19 Vaccines 2020a Frequently Asked Questions Michigan.gov/Coronavirus The information in this document will change frequently as we learn more about COVID-19 vaccines. There is a lot we are learning as the pandemic and COVID-19 vaccines evolve. The approach in Michigan will adapt as we learn more. September 29, 2021. Quick Links What’s new | Why COVID-19 vaccination is important | Booster and additional doses | What to expect when you get vaccinated | Safety of the vaccine | Vaccine distribution/prioritization | Additional vaccine information | Protecting your privacy | Where can I get more information? What’s new − Pfizer booster doses recommended for some people to boost waning immunity six months after completing the Pfizer vaccine. Why COVID-19 vaccination is important − If you are fully vaccinated, you don’t have to quarantine after being exposed to COVID-19, as long as you don’t have symptoms. This means missing less work, school, sports and other activities. − COVID-19 vaccination is the safest way to build protection. COVID-19 is still a threat, especially to people who are unvaccinated. Some people who get COVID-19 can become severely ill, which could result in hospitalization, and some people have ongoing health problems several weeks or even longer after getting infected. Even people who did not have symptoms when they were infected can have these ongoing health problems. − After you are fully vaccinated for COVID-19, you can resume many activities that you did before the pandemic. CDC recommends that fully vaccinated people wear a mask in public indoor settings if they are in an area of substantial or high transmission.
    [Show full text]
  • Recommended Adult Immunization Schedule
    Recommended Adult Immunization Schedule UNITED STATES for ages 19 years or older 2021 Recommended by the Advisory Committee on Immunization Practices How to use the adult immunization schedule (www.cdc.gov/vaccines/acip) and approved by the Centers for Disease Determine recommended Assess need for additional Review vaccine types, Control and Prevention (www.cdc.gov), American College of Physicians 1 vaccinations by age 2 recommended vaccinations 3 frequencies, and intervals (www.acponline.org), American Academy of Family Physicians (www.aafp. (Table 1) by medical condition and and considerations for org), American College of Obstetricians and Gynecologists (www.acog.org), other indications (Table 2) special situations (Notes) American College of Nurse-Midwives (www.midwife.org), and American Academy of Physician Assistants (www.aapa.org). Vaccines in the Adult Immunization Schedule* Report y Vaccines Abbreviations Trade names Suspected cases of reportable vaccine-preventable diseases or outbreaks to the local or state health department Haemophilus influenzae type b vaccine Hib ActHIB® y Clinically significant postvaccination reactions to the Vaccine Adverse Event Hiberix® Reporting System at www.vaers.hhs.gov or 800-822-7967 PedvaxHIB® Hepatitis A vaccine HepA Havrix® Injury claims Vaqta® All vaccines included in the adult immunization schedule except pneumococcal 23-valent polysaccharide (PPSV23) and zoster (RZV) vaccines are covered by the Hepatitis A and hepatitis B vaccine HepA-HepB Twinrix® Vaccine Injury Compensation Program. Information on how to file a vaccine injury Hepatitis B vaccine HepB Engerix-B® claim is available at www.hrsa.gov/vaccinecompensation. Recombivax HB® Heplisav-B® Questions or comments Contact www.cdc.gov/cdc-info or 800-CDC-INFO (800-232-4636), in English or Human papillomavirus vaccine HPV Gardasil 9® Spanish, 8 a.m.–8 p.m.
    [Show full text]
  • The Mississippi Covid-19 Vaccine Confidence Survey: Population Results Report
    MAY 2021 THE MISSISSIPPI COVID-19 VACCINE CONFIDENCE SURVEY: POPULATION RESULTS Report A collaborative population-based study The Mississippi Community Engagement Alliance Against COVID-19 Disparities (CEAL) Team The Mississippi State Department of Health: Office of Preventive Health and Health Equity EXECUTIVE SUMMARY Since the Spring of 2020, the Novel 2019 Office of Preventive Health and Health Coronavirus (COVID-19) Pandemic has Equity (OPHHE) disseminated a statewide impacted Mississippians of every race, vaccine confidence survey beginning end ethnicity, age, gender, and income bracket. of December 2020 and collecting data Unfortunately, it has disproportionately until March 2021. The survey is intended to impacted Mississippians of color, the elderly, be representative of Mississippians, with and those living with chronic disease. For intentional efforts invested to reach lower most of the past year, the State has worked income and rural Mississippi populations, as to protect its population through preventive well as the state’s Black, Hispanic (Latino/ measures such as social distancing and Latinx), Asian (including the Vietnamese personal protective equipment. However, population of the Gulf Coast), and Native with the release of COVID-19 Vaccines to American/Choctaw communities. The sur- the public, the population of Mississippi has vey was administered in three languages- the opportunity to embrace a long-term English, Spanish, and Vietnamese- through a solution to COVID-19. That is, if Mississippians mixed-modal survey effort, including: web- are willing to receive the vaccine. To based, paper-based, and verbal-oratory assess Mississippians’ COVID-19 Vaccine administration. All targeted populations confidence, the Mississippi Community were ultimately reached and are represented Engagement Alliance Against COVID-19 in the over 11,000 completed responses Disparities (CEAL) Team and the Mississippi from all 82 of Mississippi’s counties.
    [Show full text]
  • Parental Attitudes About Sexually Transmitted Infection Vaccination for Their Adolescent Children
    ARTICLE Parental Attitudes About Sexually Transmitted Infection Vaccination for Their Adolescent Children Gregory D. Zimet, PhD; Rose M. Mays, RN, PhD; Lynne A. Sturm, PhD; April A. Ravert, MS; Susan M. Perkins, PhD; Beth E. Juliar, MA, MS Objectives: To evaluate parental attitudes about adoles- Results: The mean vaccine scenario rating was 81.3. Sexu- cent vaccination as a function of vaccine characteristics, in- ally transmitted infection vaccines (mean, 81.3) were not cluding whether the vaccine prevented a sexually transmit- rated differently than non-STI vaccines (mean, 80.0). Con- tedinfection(STI),andtoexplorepossiblesociodemographic joint analysis indicated that severity of infection and vac- predictors of acceptability of STI vaccines. cine efficacy had the strongest influence on ratings, fol- lowed by availability of behavioral prevention. Mode of Design: Participants were 278 parents who accompa- transmission had a negligible effect on ratings. Child age nied their children (69.1% female, aged 12-17 years) to (P=.08) and sex (P=.77), parent age (P=.32) and educa- appointments at medical clinics. By using computer- tion (P=.34), insurance status (P=.08), and data collection based questionnaires, parents rated 9 hypothetical vac- site (P=.48) were not significantly associated with STI vac- cine scenarios, each of which was defined along 4 di- cine acceptability. mensions: mode of transmission (STI or non-STI), severity Conclusions: Parents were accepting of the idea of vac- of infection (curable, chronic, or fatal), vaccine efficacy cinating their adolescent children against STIs. The most (50%, 70%, or 90%), and availability of behavioral meth- salient issues were severity of infection and vaccine ef- ods for prevention (available or not available).
    [Show full text]