DOCSLIB.ORG

Maryland Rail Time-Of-Day Direct Ridership Model Final Report

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Maryland Rail Time-Of-Day Direct Ridership Model Final Report The National Center for Smart Growth Research and Education University of Maryland, College Park in partnership with The Maryland Department of Transportation Time-of-Day Direct Ridership Model for Maryland Rail Transit Final Report July 21st, 2017 Prepared by: Chao Liu, Ph.D., Faculty Research Associate Hiroyuki Iseki, Ph.D., Research Faculty, Assistant Professor Sicheng Wang, Research Assistant The views expressed in this report are those of The National Center for Smart Growth Research and Education, and do not necessarily represent those of the University of Maryland or the Maryland Department of Transportation, or the State of Maryland Table of Contents Executive Summary ...................................................................................................................... 3 1. Introduction – Study Objective ........................................................................................... 1 2. Study Area, Data, and Data Sources ................................................................................... 2 2.1. Rail Stations in the Model Development ......................................................................................... 2 2.2. Data and Primary Data Sources ......................................................................................................... 4 Definition of Station Area .......................................................................................................................................................... 4 Rail Ridership by Station by Time of Day ........................................................................................................................... 4 Independent Variables ................................................................................................................................................................ 6 3. Regression Analysis .............................................................................................................. 8 4. Results and Discussion ........................................................................................................ 10 4.1. Descriptive Statistics ................................................................................................................................. 10 4.2. Spatial Distribution of Key Variables ............................................................................................ 13 4.3. Model Development Results ............................................................................................................. 18 AM Model ....................................................................................................................................................................................... 19 PM Model ........................................................................................................................................................................................ 22 Off-peak Model ............................................................................................................................................................................ 23 Limitations .................................................................................................................................................................................... 24 5. Concluding Remarks .......................................................................................................... 24 Potential Applications .............................................................................................................................................................. 26 Acknowledgements ..................................................................................................................... 27 References .................................................................................................................................... 27 Appendix A. Technical Note on Baltimore Light Rail Ridership Estimation ....................... 30 Appendix B. Zero Ridership Station after Adjustments ......................................................... 36 Appendix C. Additional Maps ................................................................................................... 38 Appendix D. Alternative Models ............................................................................................... 41 Appendix E. Land Use Mix Index and Accessibility Calculation ........................................... 41 i List of Tables Table 1 Rail Stations by System ..................................................................................................... 3 Table 2 Data and Data Sources for the DRM Development ........................................................... 4 Table 3 Multimodal Stations ........................................................................................................... 6 Table 4 Ridership by Time of Day and System ............................................................................ 11 Table 5 Number of Trains by Time of Day and System ............................................................... 11 Table 6 Number of Bus Lines by System ..................................................................................... 12 Table 7 Descriptive Statistics of Selected Independent Variables ................................................ 12 Table 8 Regression Model Results by Time of Day ..................................................................... 21 Table 9 MARC Stations with Zero Ridership by Time of Day .................................................... 36 Table 10 Variables Collected and Considered but Not Included in the Final Models ................. 37 List of Figures Figure 1 Study Area and Rail Systems ........................................................................................... 3 Figure 2 Ridership by Time of day: AM Peak .............................................................................. 13 Figure 3 Ridership by Time of day: PM Peak .............................................................................. 14 Figure 4 Number of Households ................................................................................................... 15 Figure 5 Number of Total Jobs ..................................................................................................... 16 Figure 6 Number of Trains: AM Peak .......................................................................................... 17 Figure 7 Number of Bus Lines...................................................................................................... 18 Figure 8 Flow chart for estimating Baltimore Light Rail ridership .............................................. 33 Figure 9 Ridership by Time of day: Off-peak .............................................................................. 38 Figure 10 Number of Trains: PM Peak ......................................................................................... 38 Figure 11 Number of Trains: Off-peak ......................................................................................... 39 Figure 12 Parking Capacity .......................................................................................................... 39 Figure 13 Transit Accessibility ..................................................................................................... 40 ii Executive Summary In cooperation with the Maryland Transit Administration (MTA), NCSG has developed a direct ridership model (DRM) for Maryland’s rail transit systems. This DRM is a regression-based model to estimate rail transit ridership at the station level by time of day (AM peak, PM peak, and off-peak periods) based on a set of selected location-specific factors related to transit services, land use and built environment, and demographics both at the place of residence and place of work within the walksheds of rail stations. The walksheds are defined by three walking distances: quarter-mile, half-mile, and one-mile from each station of four rail systems— Baltimore Light Rail, Baltimore Metro subway, MARC commuter rail service, and the Metrorail of WMATA (Washington Metropolitan Area Transit Authority). More specifically, walksheds are created using the most updated pedestrian network that can better represent characteristics of pedestrian-oriented walking areas. The model development has involved many analyses including pre-regression descriptive analysis, regression model development, and post-regression diagnostics. The results suggest that transit service related variables are the strongest predictors of ridership and the results are consistent across models of all time periods. Parking capacity has achieved higher coefficient in the AM model, suggesting that it might be the case that more riders used park-and-ride services in the AM periods. Feeder bus service is significant and positive in both PM and off-peak models. In the variables of land use and the built environment, employment and household are the two key predictors. As expected, the number of households is significant and positive in the AM model but is not significant in the PM and off-peak models. Employment is significant in both PM and off-peak models, but is not significant in AM model. Employment categorized as midday and weekend jobs is significant and positive in the off-peak model for non-MARC stations and the coefficient is even higher than the total employment numbers in the PM model. It is also interesting
Load more

Recommended publications
  • 1997 Asa Program.Pdf
    Friday, February 21 12:00 NOON- 11:00 PM Executive Council Meeting (lunch and supper served) (Chesapeake Room NB) Saturday, February 22 8:00-9:40 AM Postgraduate Course (Constellation 3:00-5:00 PM Postgraduate Course (Constellation Ballroom A) Ballroom A) 9:40-1 0:00 AM Refreshment Break 6:00-7:00 PM Student Mixer (Maryland Suites-Balti­ 10:00-12:00 NOON Postgraduate Course (Constellation more Room) Ballroom A) 7:00-9:00 PM ASA Welcoming Reception (Atrium 12:00-1 :00 PM Lunch (on your own) Lobby) 7:00-9:00 PM Exhibits Open (Constellation Ball­ I :00-2:40 PM Postgraduate Course (Constellation Ballroom A) rooms E, F) 2:40-3:00 PM Refreshment Break 9:00- 1 I :00 PM Executive Council Meeting (Chesa­ peake Room NB) Sunday, February 23 7:45-8:00 AM Welcome and Opening Remarks 12:00-1 :30 PM Women in Andrology Luncheon (Ches­ (Constellation Ballroom A) apeake Room NB) 8:00-9:00 AM Serono Lecture: "Genetics of Prostate Business Meeting 12:00-12:30 Cancer" Patrick Walsh (Constellation Speaker and Lunch 12:30-1:30 Ballroom A) I :30-3:00 PM Symposium I: "Regulation of Testicu­ 9:00-10:00 AM American Urological Association Lec­ lar Growth and Function" (Constellation ture: "New Medical Treatments of Im­ Ballroom A) potence" Irwin Goldstein (Constella­ Patricia Morris tion Ballroom A) Martin Matzuk 10:00-10:30 AM Refreshment Break/Exhibits 3:00-3:30 PM Refreshment Break/Exhibits (Constellation Ballrooms E, F) (Constellation Ballrooms E, F) 10:30-12:00 NOON Oral Session I: "Genes and Male Repro­ 3:30-4:30 PM Oral Session II: "Calcium Channels duction" (Constellation Ballroom A) and Male Reproduction" (Constellation Ballroom A) 12:00- 1 :30 PM Lune (on your own) � 4:30-6:30 PM Poster Session I (Constellation Ball­ �4·< rooms C, D) \v\wr 7:30-11:00 PM Banquet (National Aquarium) Monday, February 24 7:00-8:00 AM Past Presidents' Breakfast 12:00-1 :30 PM Simultaneous Events: (Pratt/Calvert Rooms) I.
    [Show full text]
  • Public Transportation
    TRANSPORTATION NETWORK DIRECTORY FOR PEOPLE WITH DISABILITIES AND ADULTS 50+ MONTGOMERY COUNTY, MD PUBLIC TRANSPORTATION Montgomery County, Maryland (‘the County’) cannot guarantee the relevance, completeness, accuracy, or timeliness of the information provided on the non-County links. The County does not endorse any non-County organizations' products, services, or viewpoints. The County is not responsible for any materials stored on other non-County web sites, nor is it liable for any inaccurate, defamatory, offensive or illegal materials found on other Web sites, and that the risk of injury or damage from viewing, hearing, downloading or storing such materials rests entirely with the user. Alternative formats of this document are available upon request. This is a project of the Montgomery County Commission on People with Disabilities. To submit an update, add or remove a listing, or request an alternative format, please contact: [email protected], 240-777-1246 (V), MD Relay 711. MetroAccess and Abilities-Ride MetroAccess Paratransit – Washington Metropolitan Area Transit Authority (WMATA) MetroAccess is a shared-ride, door-to-door public transportation service for people who are unable to use fixed-route public transit due to disability. "Shared ride" means that multiple passengers may ride together in the same vehicle. The service provides daily trips throughout the Transit Zone in the Washington Metropolitan region. The Transit Zone consists of the District of Columbia, Montgomery and Prince George’s Counties in Maryland, Arlington and Fairfax Counties and the cities of Alexandria, Fairfax and Falls Church in Northern Virginia. Rides are offered in the same service areas and during the same hours of operation as Metrorail and Metrobus.
    [Show full text]
  • Hearing from You Michael S
    Robert L. Ehrlich, Jr. CONTACT US: Governor Hearing From You Michael S. Steele For further information about this project, please contact: Lt. Governor Fall 2004 Open Houses Lorenzo Bryant, Project Manager En Español: Jose M. Vazquéz Robert L. Flanagan Maryland Transit Administration Maryland Transit Administration MDOT Secretary 6 Saint Paul Street, 9th Floor 8720 Georgia Avenue, Suite 904 Plan to Attend Almost 300 people attended seven Red Line Open Houses Silver Spring, MD 20910 held between October 26 and November 9, 2004. At the Baltimore, MD 21202 Upcoming Public Open Open Houses, participants received updates on the status Lisa L. Dickerson (301) 565-9665 of the project, provided input, and received information on MTA Acting Administrator Telephone: 410-767-3754 Houses on the Red Line alternatives under study. The Open Houses were advertised in a project mailer and the website, as well as local newspapers. 410-539-3497 TTY The Maryland Transit Administration (buildings, historic districts, archaeological Fliers were also distributed to locations along the Red Line (MTA), in cooperation with Baltimore City, or cultural sites) that are eligible for the corridor. Materials presented at the Open Houses can Email: [email protected] | [email protected] Baltimore County, and federal and state National Register of Historic Places. If be viewed by logging on to the project website, resource agencies, will be preparing a you are interested in participating in the www.baltimoreregiontransitplan.com. Website: www.baltimoreregiontransitplan.com Draft Environmental Impact Statement Section 106-Public Involvement process, (DEIS) for the Red Line Study. preservation specialists will be available at Major themes from the Open House comments received Alternate formats of Red Line information can be provided upon request.
    [Show full text]
  • November 6, 2014 for Those of You Who Were Able to Join Us at Our
    Dear All: November 6, 2014 For those of you who were able to join us at our WB&A Members Only Semi‐Annual General Membership/Swap Meet it was good to see you and we are glad you were able to join us. Please join us in welcoming and congratulating the winners of the 2015‐16 election: David Eadie (BoD & Membership); Bob Goodrich (BoD); Bill Moss (BoD) and Dan Danielson (Eastern Rep). I extend the entire BoD thanks and welcoming to them for the 2015‐16 Term. At our meeting we took a few minutes to say “thank you” to a couple who have done so much for the train hobby, the TCA and the WB&A, namely, Mary and Pete Jackson. Your BoD presented them with a plaque in honor of their work on the BoD over the years and for their years of work running Kids Korner at York and for the countless other ways they have assisted. Mary and Pete moved to Delaware about 2 years ago and have continued to be active in all that they had committed themselves to, but it’s time for them to take time to play trains and let others step up to take on the roles they had. So to Mary and Pete we say thank you for your years of service. As a reminder, the eblasts and attachments will be placed on the WB&A website under the “About” tab for your viewing/sharing pleasure http://www.wbachapter.org/2014%20E‐ Blast%20Page.htm The attachments are contained in the one PDF attached to this email in an effort to streamline the sending of this email and to ensure the attachments are able to be received.
    [Show full text]
  • Metrorail/Coconut Grove Connection Study Phase II Technical
    METRORAILICOCONUT GROVE CONNECTION STUDY DRAFT BACKGROUND RESEARCH Technical Memorandum Number 2 & TECHNICAL DATA DEVELOPMENT Technical Memorandum Number 3 Prepared for Prepared by IIStB Reynolds, Smith and Hills, Inc. 6161 Blue Lagoon Drive, Suite 200 Miami, Florida 33126 December 2004 METRORAIUCOCONUT GROVE CONNECTION STUDY DRAFT BACKGROUND RESEARCH Technical Memorandum Number 2 Prepared for Prepared by BS'R Reynolds, Smith and Hills, Inc. 6161 Blue Lagoon Drive, Suite 200 Miami, Florida 33126 December 2004 TABLE OF CONTENTS 1.0 INTRODUCTION .................................................................................................. 1 2.0 STUDY DESCRiPTION ........................................................................................ 1 3.0 TRANSIT MODES DESCRIPTION ...................................................................... 4 3.1 ENHANCED BUS SERViCES ................................................................... 4 3.2 BUS RAPID TRANSIT .............................................................................. 5 3.3 TROLLEY BUS SERVICES ...................................................................... 6 3.4 SUSPENDED/CABLEWAY TRANSIT ...................................................... 7 3.5 AUTOMATED GUIDEWAY TRANSiT ....................................................... 7 3.6 LIGHT RAIL TRANSIT .............................................................................. 8 3.7 HEAVY RAIL ............................................................................................. 8 3.8 MONORAIL
    [Show full text]
  • 1 United States of America Department of Transportation Departmental Office of Civil Rights Federal Highway Administration Offic
    UNITED STATES OF AMERICA DEPARTMENT OF TRANSPORTATION DEPARTMENTAL OFFICE OF CIVIL RIGHTS FEDERAL HIGHWAY ADMINISTRATION OFFICE OF CIVIL RIGHTS BALTIMORE REGIONAL INITIATIVE DEVELOPING GENUINE EQUALITY, INC., and EARL ANDREWS, Individually, Complainants, vs. Docket No. STATE OF MARYLAND, MARYLAND DEPARTMENT OF TRANSPORTATION, MARYLAND TRANSIT ADMINISTRATION, and MARYLAND STATE HIGHWAY ADMINISTRATION; Respondents. COMPLAINT PURSUANT TO TITLE VI OF THE CIVIL RIGHTS ACT OF 1964 1 On June 25, 2015, Maryland Governor, Larry Hogan, announced that the State had cancelled construction of the Red Line, a light rail line set to run east-west through the Baltimore region, and that all state funding for it would be redirected to a newly-created Highways, Bridges, and Roads Initiative, focusing on road projects in rural and suburban parts of the state.1 In doing so, Maryland forfeited $900 million in federal funds designated for the Line and abandoned a twelve-year planning process on which the State and federal government had expended approximately $288 million.2 A transportation economist, using Maryland’s own travel model, found that whites will receive 228 percent of the net benefit from the decision, while African Americans will receive -124 percent. The decision to cancel the Red Line and divert the resources elsewhere was only the latest in the State’s long historical pattern of deprioritizing the needs of Baltimore’s3 primarily African-American population,4 many of whom are dependent on public transportation.5 1 Michael Dresser & Luke Broadwater, Hogan Says No to Red Line, Yes to Purple, Balt. Sun (June 25, 2015), available at http://www.baltimoresun.com/news/maryland/politics/bs-md- hogan-transportation-20150624-story.html; Ex.
    [Show full text]
  • CHRISTOPHER PATTON, Plaintiff, V. SEPTA, Faye LM Moore, and Cecil
    IN THE UNITED STATES DISTRICT COURT FOR THE EASTERN DISTRICT OF PENNSYLVANIA : CHRISTOPHER PATTON, : Plaintiff, : CIVIL ACTION : v. : NO. 06-707 : SEPTA, Faye L. M. Moore, : and Cecil W. Bond Jr., : Defendants. : Memorandum and Order YOHN, J. January ___, 2007 Plaintiff Christopher Patton brings the instant action pursuant to the Americans with Disabilities Act, 42 U.S.C. § 12101 et seq . (“ADA”); the Rehabilitation Act, 29 U.S.C. § 701 et seq.; 42 U.S.C. § 1983; the Pennsylvania Human Relations Act, 43 Pa. Cons. Stat. § 955(a) (“PHRA”); and Article I of the Pennsylvania Constitution, against defendants Southeastern Pennsylvania Transportation Authority (“SEPTA”); SEPTA’s General Manager, Faye L. M. Moore; and SEPTA’s Assistant General Manager, Cecil W. Bond Jr. (collectively, “defendants”). Presently before the court is defendants’ motion to dismiss pursuant to Federal Rule of Civil Procedure 12(b)(6) or, in the alternative, for summary judgment pursuant to Federal Rule of Civil Procedure 56, as to plaintiff’s claims under the PHRA against defendants Moore and Bond (Counts VII and VIII), plaintiff’s claims for violation of the Pennsylvania Constitution (Counts XI, XII, and XIII) and plaintiff’s demand for punitive damages. For the following reasons, defendants’ motion will be granted in part and denied in part. 1 I. Factual and Procedural Background A. Plaintiff’s Factual Allegations Plaintiff was hired by SEPTA on December 8, 1997 to develop and direct its Capital and Long Range Planning Department. (Second Am. Compl. (“Compl.”) ¶ 14.) Defendant Moore, is the General Manager of SEPTA (id . at ¶¶ 6, 13); defendant Bond is the Assistant General Manager of SEPTA (id.
    [Show full text]
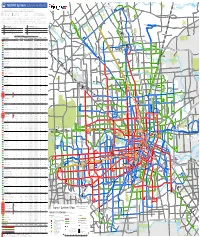
  • TRANSIT SYSTEM MAP Local Routes E
    Non-Metro Service 99 Woodlands Express operates three Park & 99 METRO System Sistema de METRO Ride lots with service to the Texas Medical W Center, Greenway Plaza and Downtown. To Kingwood P&R: (see Park & Ride information on reverse) H 255, 259 CALI DR A To Townsen P&R: HOLLOW TREE LN R Houston D 256, 257, 259 Northwest Y (see map on reverse) 86 SPRING R E Routes are color-coded based on service frequency during the midday and weekend periods: Medical F M D 91 60 Las rutas están coloradas por la frecuencia de servicio durante el mediodía y los fines de semana. Center 86 99 P&R E I H 45 M A P §¨¦ R E R D 15 minutes or better 20 or 30 minutes 60 minutes Weekday peak periods only T IA Y C L J FM 1960 V R 15 minutes o mejor 20 o 30 minutos 60 minutos Solo horas pico de días laborales E A D S L 99 T L E E R Y B ELLA BLVD D SPUR 184 FM 1960 LV R D 1ST ST S Lone Star Routes with two colors have variations in frequency (e.g. 15 / 30 minutes) on different segments as shown on the System Map. T A U College L E D Peak service is approximately 2.5 hours in the morning and 3 hours in the afternoon. Exact times will vary by route. B I N N 249 E 86 99 D E R R K ") LOUETTA RD EY RD E RICHEY W A RICH E RI E N K W S R L U S Rutas con dos colores (e.g.
    [Show full text]
  • Rider Guide / Guía De Pasajeros
    Updated 02/10/2019 Rider Guide / Guía de Pasajeros Stations / Estaciones Stations / Estaciones Northline Transit Center/HCC Theater District Melbourne/North Lindale Central Station Capitol Lindale Park Central Station Rusk Cavalcade Convention District Moody Park EaDo/Stadium Fulton/North Central Coffee Plant/Second Ward Quitman/Near Northside Lockwood/Eastwood Burnett Transit Center/Casa De Amigos Altic/Howard Hughes UH Downtown Cesar Chavez/67th St Preston Magnolia Park Transit Center Central Station Main l Transfer to Green or Purple Rail Lines (see map) Destination Signs / Letreros Direccionales Westbound – Central Station Capitol Eastbound – Central Station Rusk Eastbound Theater District to Magnolia Park Hacia el este Magnolia Park Main Street Square Bell Westbound Magnolia Park to Theater District Downtown Transit Center Hacia el oeste Theater District McGowen Ensemble/HCC Wheeler Transit Center Museum District Hermann Park/Rice U Stations / Estaciones Memorial Hermann Hospital/Houston Zoo Theater District Dryden/TMC Central Station Capitol TMC Transit Center Central Station Rusk Smith Lands Convention District Stadium Park/Astrodome EaDo/Stadium Fannin South Leeland/Third Ward Elgin/Third Ward Destination Signs / Letreros Direccionales TSU/UH Athletics District Northbound Fannin South to Northline/HCC UH South/University Oaks Hacia el norte Northline/HCC MacGregor Park/Martin Luther King, Jr. Southbound Northline/HCC to Fannin South Palm Center Transit Center Hacia el sur Fannin South Destination Signs / Letreros Direccionales Eastbound Theater District to Palm Center TC Hacia el este Palm Center Transit Center Westbound Palm Center TC to Theater District Hacia el oeste Theater District The Fare/Pasaje / Local Make Your Ride on METRORail Viaje en METRORail Rápido y Fare Type Full Fare* Discounted** Transfer*** Fast and Easy Fácil Tipo de Pasaje Pasaje Completo* Descontado** Transbordo*** 1.
    [Show full text]
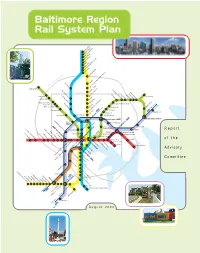
  • Baltimore Region Rail System Plan Report
    Baltimore Region Rail System Plan Report of the Advisory Committee August 2002 Advisory Committee Imagine the possibilities. In September 2001, Maryland Department of Transportation Secretary John D. Porcari appointed 23 a system of fast, convenient and elected, civic, business, transit and community leaders from throughout the Baltimore region to reliable rail lines running throughout serve on The Baltimore Region Rail System Plan Advisory Committee. He asked them to recommend the region, connecting all of life's a Regional Rail System long-term plan and to identify priority projects to begin the Plan's implemen- important activities. tation. This report summarizes the Advisory Committee's work. Imagine being able to go just about everywhere you really need to go…on the train. 21 colleges, 18 hospitals, Co-Chairs 16 museums, 13 malls, 8 theatres, 8 parks, 2 stadiums, and one fabulous Inner Harbor. You name it, you can get there. Fast. Just imagine the possibilities of Red, Mr. John A. Agro, Jr. Ms. Anne S. Perkins Green, Blue, Yellow, Purple, and Orange – six lines, 109 Senior Vice President Former Member We can get there. Together. miles, 122 stations. One great transit system. EarthTech, Inc. Maryland House of Delegates Building a system of rail lines for the Baltimore region will be a challenge; no doubt about it. But look at Members Atlanta, Boston, and just down the parkway in Washington, D.C. They did it. So can we. Mr. Mark Behm The Honorable Mr. Joseph H. Necker, Jr., P.E. Vice President for Finance & Dean L. Johnson Vice President and Director of It won't happen overnight.
    [Show full text]
  • Accessible Transportation Options for People with Disabilities and Senior Citizens
    Accessible Transportation Options for People with Disabilities and Senior Citizens In the Washington, D.C. Metropolitan Area JANUARY 2017 Transfer Station Station Features Red Line • Glenmont / Shady Grove Bus to Airport System Orange Line • New Carrollton / Vienna Parking Station Legend Blue Line • Franconia-Springfield / Largo Town Center in Service Map Hospital Under Construction Green Line • Branch Ave / Greenbelt Airport Full-Time Service wmata.com Yellow Line • Huntington / Fort Totten Customer Information Service: 202-637-7000 Connecting Rail Systems Rush-Only Service: Monday-Friday Silver Line • Wiehle-Reston East / Largo Town Center TTY Phone: 202-962-2033 6:30am - 9:00am 3:30pm - 6:00pm Metro Transit Police: 202-962-2121 Glenmont Wheaton Montgomery Co Prince George’s Co Shady Grove Forest Glen Rockville Silver Spring Twinbrook B30 to Greenbelt BWI White Flint Montgomery Co District of Columbia College Park-U of Md Grosvenor - Strathmore Georgia Ave-Petworth Takoma Prince George’s Plaza Medical Center West Hyattsville Bethesda Fort Totten Friendship Heights Tenleytown-AU Prince George’s Co Van Ness-UDC District of Columbia Cleveland Park Columbia Heights Woodley Park Zoo/Adams Morgan U St Brookland-CUA African-Amer Civil Dupont Circle War Mem’l/Cardozo Farragut North Shaw-Howard U Rhode Island Ave Brentwood Wiehle-Reston East Spring Hill McPherson Mt Vernon Sq NoMa-Gallaudet U New Carrollton Sq 7th St-Convention Center Greensboro Fairfax Co Landover Arlington Co Tysons Corner Gallery Place Union Station Chinatown Cheverly 5A to
    [Show full text]
  • Service Guidelines and Standards
    Service Guidelines and Standards Revised Summer 2015 Capital Metropolitan Transportation Authority | Austin, Texas TABLE OF CONTENTS INTRODUCTION Purpose 3 Overview 3 Update 3 Service Types 4 SERVICE GUIDELINES Density and Service Coverage 5 Land Use 6 Destinations and Activity Centers 6 Streets and Sidewalk Characteristics 7 Demographic and Socioeconomic Characteristics 7 Route Directness 8 Route Deviation 9 Two-way Service 10 Branching and Short-Turns 10 Route Spacing 11 Route Length 11 Route Terminals 11 Service Span 12 Service Frequency 12 Bus Stop Spacing 13 Bus Stop Placement 13 Bus Stop Amenities 14 MetroRapid Stations vs. Bus Stops 15 Transit Centers and Park & Rides 15 SERVICE STANDARDS Schedule Reliability 19 Load Factors 19 Ridership Productivity and Cost-Effectiveness 20 Potential Corrective Actions 21 New and Altered Services 21 Service Change Process 22 APPENDIX A1: Map – Households without Access to an Automobile 24 A2: Map – Elderly Population Exceeding 10% of Total Population 25 A3: Map - Youth Population Exceeding 25% by Census Block 26 A4: Map – Household Income Below 50% of Regional Median 27 B1: Chart – Park & Ride Level of Service (LOS) Amenities 28 Service Guidelines and Standards INTRODUCTION Purpose The Capital Metropolitan Transportation Authority connects people, jobs and communities by providing quality transportation choices. Service guidelines and standards reflect the goals and objectives of the Authority. Capital Metro Strategic Goals: 1) Provide a Great Customer Experience 2) Improve Business Practices 3) Demonstrate the Value of Public Transportation in an Active Community 4) Be a Regional Leader Overview Service guidelines provide a framework for the provision, design, and allocation of service. Service guidelines incorporate transit service planning factors including residential and employment density, land use, activity centers, street characteristics, and demographics.
    [Show full text]