Probability Model of Hangzhou Bay Bridge Vehicle Loads Using Weigh-In-Motion Data
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

2006 EXECUTIVE COMMITTEE Kenneth J
2006 EXECUTIVE COMMITTEE Kenneth J. Wright, PE Thomas G. Leech, PE, SE HDR Engineering, Inc. Gannett Fleming, Inc. General Chair Magazine Chair M. Myint Lwin, PE, SE Herbert M. Mandel, PE Federal Highway GAI Consultants, Inc. Administration Technical Program Chair Matthew P. McTish, PE McTish, Kunkel & Associates Al M. Ahmed, PE Exhibits Chair A&A Consultants Inc. Gerald Pitzer, PE Michael J. Alterio GAI Consultants, Inc. Alpha Structures Inc. Gary Runco, PE Carl Angeloff, PE Paul C. Rizzo Associates, Inc. Bayer MaterialScience, LLC Seminars Chair Awards Chair Helena Russell Victor E. Bertolina, PE Bridge, design & engineering SAI Consulting Engineers Awards – Vice Chair Budget Chair Louis J. Ruzzi, PE Enrico T. Bruschi, PE Pennsylvania Department DMJM Harris of Transportation Jeffrey J. Campbell, PE Thomas J. Vena, PE Michael Baker, Jr., Inc. Allegheny County Department of Public Works Richard Connors, PE, PMP McCormick Taylor, Inc. Lisle E. Williams, PE, PLS Rules Chair DMJM Harris Attendance & Co-Sponsors James D. Dwyer Chair STV, Inc. Emeritus Committee Gary L. Graham, PE Members Pennsylvania Turnpike Joel Abrams, PhD Commission Consultant Kent A. Harries, PhD, PEng Reidar Bjorhovde, PhD University of Pittsburgh The Bjorhovde Group Student Awards Chair Steven Fenves, PhD Donald W. Herbert, PE NIST Pennsylvania Department of Transportation Arthur W. Hedgren, Jr., PhD, PE Donald Killmeyer, Jr., PE Consultant ms consultants, inc. Tour Chair John F. Graham, Jr., PE Graham Consulting Inc. Eric S. Kline KTA-Tator, Inc. Keynote & Special Interest Session Chair ADVANCING BRIDGE TECHNOLOGY GLOBALLY ○○○○○○ ○○○○○○○○○○○○○○○○○○○○○○○○ 1 2006 CHAIRMAN’S MESSAGE Kenneth J. Wright, PE HDR Engineering, Inc. 2006 IBC General Chairman As this year’s General Chairman, I am pleased to wel- come you to the 2006 International Bridge Conference in Pittsburgh, the “City of Bridges”. -
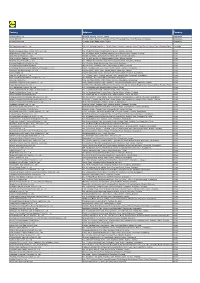
Factory Address Country
Factory Address Country Durable Plastic Ltd. Mulgaon, Kaligonj, Gazipur, Dhaka Bangladesh Lhotse (BD) Ltd. Plot No. 60&61, Sector -3, Karnaphuli Export Processing Zone, North Potenga, Chittagong Bangladesh Bengal Plastics Ltd. Yearpur, Zirabo Bazar, Savar, Dhaka Bangladesh ASF Sporting Goods Co., Ltd. Km 38.5, National Road No. 3, Thlork Village, Chonrok Commune, Korng Pisey District, Konrrg Pisey, Kampong Speu Cambodia Ningbo Zhongyuan Alljoy Fishing Tackle Co., Ltd. No. 416 Binhai Road, Hangzhou Bay New Zone, Ningbo, Zhejiang China Ningbo Energy Power Tools Co., Ltd. No. 50 Dongbei Road, Dongqiao Industrial Zone, Haishu District, Ningbo, Zhejiang China Junhe Pumps Holding Co., Ltd. Wanzhong Villiage, Jishigang Town, Haishu District, Ningbo, Zhejiang China Skybest Electric Appliance (Suzhou) Co., Ltd. No. 18 Hua Hong Street, Suzhou Industrial Park, Suzhou, Jiangsu China Zhejiang Safun Industrial Co., Ltd. No. 7 Mingyuannan Road, Economic Development Zone, Yongkang, Zhejiang China Zhejiang Dingxin Arts&Crafts Co., Ltd. No. 21 Linxian Road, Baishuiyang Town, Linhai, Zhejiang China Zhejiang Natural Outdoor Goods Inc. Xiacao Village, Pingqiao Town, Tiantai County, Taizhou, Zhejiang China Guangdong Xinbao Electrical Appliances Holdings Co., Ltd. South Zhenghe Road, Leliu Town, Shunde District, Foshan, Guangdong China Yangzhou Juli Sports Articles Co., Ltd. Fudong Village, Xiaoji Town, Jiangdu District, Yangzhou, Jiangsu China Eyarn Lighting Ltd. Yaying Gang, Shixi Village, Shishan Town, Nanhai District, Foshan, Guangdong China Lipan Gift & Lighting Co., Ltd. No. 2 Guliao Road 3, Science Industrial Zone, Tangxia Town, Dongguan, Guangdong China Zhan Jiang Kang Nian Rubber Product Co., Ltd. No. 85 Middle Shen Chuan Road, Zhanjiang, Guangdong China Ansen Electronics Co. Ning Tau Administrative District, Qiao Tau Zhen, Dongguan, Guangdong China Changshu Tongrun Auto Accessory Co., Ltd. -

SHOCK CONTROL of BRIDGES in CHINA USING TAYLOR DEVICES’ FLUID VISCOUS DEVICES 1 1 2 2 Chen Yongqi Ma Liangzhe Cao Tiezhu1 Robert Schneider Craig Winters
th The 14 World Conference on Earthquake Engineering October 12-17, 2008, Beijing, China SHOCK CONTROL OF BRIDGES IN CHINA USING TAYLOR DEVICES’ FLUID VISCOUS DEVICES 1 1 2 2 Chen Yongqi Ma Liangzhe Cao Tiezhu1 Robert Schneider Craig Winters 1Beijing Qitai Shock Control and Scientific Development Co.,Ltd , Beijing 100037, China 2Taylor Devices, Inc. North Tonawanda, NY 14120, USA Email: [email protected], ABSTRACT : Fluid Viscous Devices are a successful structural protective system for bridge vibration. The structural protective technique and the dampers have been introduced to China since 1999. The Taylor Devices’ damper systems has already been successfully installed or will be installed in large or the super large bridges in China for protection from earthquake, wind. vehicle and other vibration. Seventeen different bridge projects introduced here include the Sutong Yangtze River Bridge, the longest cable stayed bridge in the world, the Nanjing 3rd Yangtze River Bridge, the fifth longest suspension bridge in the world, and the Xihoumen Across Sea Bridge, the second longest suspension bridge in the world. The performance of the bridges and dampers have been reported as “very good” during the May 12, 2008 Wenchuan earthquake. All of the dampers produced have been subjected to rigorous static and dynamic testing, which show the dampers will perform well for the next 50 years and possibly a lot longer. KEYWORDS: Lock-Up Devices, Fluid Viscous Dampers, Limited Displacement Damper 1. INTRODUCTION Along with the rapid economic development in China over the past two decades, a large number of highways and bridges have been built in China. By 2004 China constructed 1.81 millions kilometers of roads and 30 thousand kilometers of highways. -

China's Major Bridges Summary 1. Background
China’s Major Bridges Maorun FENG Maorun Feng, born in 1942, graduated from the Tangshan Professor Railway Institute with a Master’s Chairman of Technical degree, has been engaged in the Consultative Committee, design and research of bridges for 40 Ministry of years. He is the Chairman of Technical Consultative Committee Communications and the Former Chief Engineer of the Beijing, China State Ministry of Communications. He is also the current Chairman of China Association of Highway and Waterway Engineering Consultants. [email protected] . Summary In response to continuous economic development over the past 30 years, China has mobilized a program of large scale bridge construction. The technology of various types of bridges, including girder bridges, arch bridges, and cable-supported bridges, has been developed rapidly. Bridge spanning capacity has been continuously improved. Girder bridges with main span of 330 m, arch bridges with main span of 550 m, cable-stayed bridges with main span of 1088 m and suspension bridges with main span of 1650 m have already been built. Moreover, two sea-crossing bridges with overall length over 30 km have also been opened to traffic. This paper briefly introduces China’s major bridges, including girder bridges with spans greater than 200 m, arch bridges with spans greater than 400 m, cable-stayed bridges with spans greater than 600 m, and suspension bridges with spans greater than 1200 m. These bridges represent technological progress in such aspects as structural system, materials, as well as construction methods and equipment. Key words: girder bridge, arch bridge, cable-supported bridge, cable-stayed bridge, suspension bridge, steel-concrete composite bridge 1. -

Capitalism from Below
CAPITALISM FROM BELOW Angemeldet | [email protected] Heruntergeladen am | 22.05.13 14:32 Angemeldet | [email protected] Heruntergeladen am | 22.05.13 14:32 CAPITALISM FROM BELOW Markets and Institutional Change in China VICTOR NEE SONJA OPPER HARVARD UNIVERSITY PRESS Cambridge, Massachusetts, and London, England 2012 Angemeldet | [email protected] Heruntergeladen am | 22.05.13 14:32 Copyright © 2012 by the President and Fellows of Harvard College All rights reserved Printed in the United States of America Library of Congress Cataloging- in- Publication Data Nee, Victor Capitalism from below : markets and institutional change in China / Victor Nee, Sonja Opper. p. cm. Includes bibliographical references and index. ISBN 978- 0- 674- 05020-4 (alk. paper) 1. Capitalism— China. 2. Entrepreneurship— China. 3. Industrial policy— China. 4. China—Economic policy. 5. China— Politics and government. I. Opper, Sonja. II. Title. HC427.95.N44 2012 330.951—dc23 2011042367 Angemeldet | [email protected] Heruntergeladen am | 22.05.13 14:32 To Margaret Nee (1919– 2011) and Fanny de Bary (1922– 2009) Margret and Herbert Opper Angemeldet | [email protected] Heruntergeladen am | 22.05.13 14:32 Angemeldet | [email protected] Heruntergeladen am | 22.05.13 14:32 Contents List of Figures and Tables ix Acknowledgments xiii 1 Where Do Economic Institutions Come From? 1 2 Markets and Endogenous Institutional Change 12 3 Th e Epicenter of Bottom-Up Capitalism 41 4 Entrepreneurs and Institutional Innovation 72 5 Legitimacy and Or gan i za tion -

Chongming-Qidong Yangtze River Highway Bridge (Hereinafter “Chongqi Bridge”) Has a Length of 6.84Km
Address (no P.O. Box ): Building A, 85, Deshengmenwai Street, Xicheng District, Beijing City with postal code: Beijing, 10088 Country: China Phone (with country code): +86-10-82017778 Fax:+86-10-82017738 E-mail for communication on the submission: [email protected] Name of contact person, if different than CEO: [email protected] Date and signature of CEO: May 15th, 2015 Questions to be responded to by the firm submitting the application Why do you think this project should receive an award? How does it demonstrate: z innovation, quality, and professional excellence z transparency and integrity in the management and project implementation z sustainability and respect for the environment Chongming-Qidong Yangtze River Highway Bridge (hereinafter “Chongqi Bridge”) has a length of 6.84km. It was scheduled to be completed by April, 2012, but eventually opened to traffic on December 24th, 2011. By now it has been in operation for 3 years and 4 months. The client is Jiangsu Province Chongqi Bridge Construction Headquarters. The main bridge of Chongqi Bridge is a six-span continuous steel box girder bridge with span arrangement of 102m+4×185m+102m=944m. The bridge deck structure is formed by double haunched continuous steel box girders with vertical webs. The width of single girder is 16.1m. The girder depth varies in parabolic, 3.5m at the ends of side spans, 4.8m at the mid span and 9.0m at main piers. The girders were erected span by span with one single segment in each span without any stitching segment between them. -

Sustainable Development of New Urbanization from the Perspective of Coordination: a New Complex System of Urbanization-Technology Innovation and the Atmospheric Environment
atmosphere Article Sustainable Development of New Urbanization from the Perspective of Coordination: A New Complex System of Urbanization-Technology Innovation and the Atmospheric Environment Bin Jiang 1, Lei Ding 1,2,* and Xuejuan Fang 3 1 School of International Business & Languages, Ningbo Polytechnic, Ningbo 315800, Zhejiang, China; [email protected] 2 Institute of Environmental Economics Research, Ningbo Polytechnic, Ningbo 315800, Zhejiang, China 3 Ningbo Institute of Oceanography, Ningbo 315832, Zhejiang, China; [email protected] * Correspondence: [email protected] Received: 26 September 2019; Accepted: 25 October 2019; Published: 28 October 2019 Abstract: Exploring the coordinated development of urbanization (U), technology innovation (T), and the atmospheric environment (A) is an important way to realize the sustainable development of new-type urbanization in China. Compared with existing research, we developed an integrated index system that accurately represents the overall effect of the three subsystems of UTA, and a new weight determination method, the structure entropy weight (SEW), was introduced. Then, we constructed a coordinated development index (CDI) of UTA to measure the level of sustainability of new-type urbanization. This study also analyzed trends observed in UTA for 11 cities in Zhejiang Province of China, using statistical panel data collected from 2006 to 2017. The results showed that: (1) urbanization efficiency, the benefits of technological innovation, and air quality weigh the most in the indicator systems, which indicates that they are key factors in the behavior of UTA. The subsystem scores of the 11 cities show regional differences to some extent. (2) Comparing the coordination level of UTA subsystems, we found that the order is: coordination degree of UT > coordination degree of UA > coordination degree of TA. -

Delft University of Technology Local Human Activities Overwhelm
Delft University of Technology Local human activities overwhelm decreased sediment supply from the Changjiang River Continued rapid accumulation in the Hangzhou Bay-Qiantang Estuary system Xie, Dongfeng; Pan, Cunhong; Wu, Xiuguang; Gao, Shu; Wang, Zheng Bing DOI 10.1016/j.margeo.2017.08.013 Publication date 2017 Document Version Accepted author manuscript Published in Marine Geology Citation (APA) Xie, D., Pan, C., Wu, X., Gao, S., & Wang, Z. B. (2017). Local human activities overwhelm decreased sediment supply from the Changjiang River: Continued rapid accumulation in the Hangzhou Bay-Qiantang Estuary system. Marine Geology, 392, 66-77. https://doi.org/10.1016/j.margeo.2017.08.013 Important note To cite this publication, please use the final published version (if applicable). Please check the document version above. Copyright Other than for strictly personal use, it is not permitted to download, forward or distribute the text or part of it, without the consent of the author(s) and/or copyright holder(s), unless the work is under an open content license such as Creative Commons. Takedown policy Please contact us and provide details if you believe this document breaches copyrights. We will remove access to the work immediately and investigate your claim. This work is downloaded from Delft University of Technology. For technical reasons the number of authors shown on this cover page is limited to a maximum of 10. © 2017 Manuscript version made available under CC-BY-NC-ND 4.0 license https://creativecommons.org/licenses/by-nc-nd/4.0/ Postprint of Marine Geology Volume 392, 1 October 2017, Pages 66-77 Link to formal publication (Elsevier): https://doi.org/10.1016/j.margeo.2017.08.013 1 Local human activities overwhelm decreased sediment from the Changjiang 2 River: continued rapid accumulation in the Hangzhou Bay-Qiantang Estuary 3 Dongfeng Xiea,*, Cunhong Pana, Xiuguangsystem Wua, Shu Gaob, Zhengbing Wangc,d 4 aZhejiang Institute of Hydraulics and Estuary, Hangzhou, China. -

Safety Management and Emergency Relief of Hangzhou Bay Bridge
Forum on China-US Transportation Symposium中国 on·杭州湾跨海大桥 Safety and Disaster -relief Coordination Hangzhou Bay Bridge Safety Management and Emergency Relief of Hangzhou Bay Bridge -- Department of Communications of Zhejiang Province 中国·杭州湾跨海大桥 Hangzhou Bay Bridge Preface Overview Safety Management Emergency Relief Difficulties and Challenges 中国·杭州湾跨海大桥 Hangzhou Bay Bridge Preface-Overview of Bridge in Zhejiang • Zhejiang owns a great number of bridges. Till 2011, the number has been 45578, among which 196 bridges are super large bridges, such as Hangzhou Bay Bridge, Zhoushan Bridge, Jiashao Bridge (under construction), Xiangshangang Bridge (under construction). • The management system of the roads and bridges in Zhejiang consists of government leading, industry regulation and owner in-charge. • Recently, Zhejiang Province is consistently exploring and practicing the Safety Management and Emergency Relief of super large bridges. Experiences will be introduced, taking Hangzhou Bay Bridge as an example. 中国·杭州湾跨海大桥 Hangzhou Bay Bridge Overview • Length of 36 km • Investment of 13.4 billion • Highway • Dual-direction, six-lane 中国·杭州湾跨海大桥 Hangzhou Bay BridgeOverview -Role in the Economy Shanghai Hangzhou Bay Bridge Shorten by 120km Ningbo 中国·杭州湾跨海大桥 Hangzhou Bay Bridge Overview—Quality &Safety • Second Prize of National Science and Technology Progress Award, 2011. • China Construction Luban Award, 2010-2011. • Zhan Tianyou Award of China Civil Engineering, 2011. • Construction Safety: Ten Billion RMB Output with Zero Death 中国·杭州湾跨海大桥 Hangzhou Bay BridgeOverview -Administration System • Formulate the Regulating Rules of Hangzhou Bay Bridge ABHBB • Set up the Administration Bureau of Hangzhou Bay Bridge (ABHBB) Law Enforcement Traffic police Agent of High Way Leader: Administration Bureau Main body: Owner Corporation Hangzhou Bay Bridge Co., LTD Guarantee: Logistics departments Supporter: Maintenance centers Maintenance Contractors Center 中国·杭州湾跨海大桥 Hangzhou Bay BridgeSafety Management-Operational Condition Small-range disastrous climate is common. -

THE GRAND CANAL of CHINA
FEATURE THE GRAND CANAL of CHINA By Ruby Tsao s the site of the international G20 communication, transportation, trade, economic meeting held on September 4-5, 2016, development, cultural exchange and unification A all eyes were on the city of Hangzhou. of China since ancient times. “Heaven above, Suzhou and Hangzhou below” is BACKGROUND a saying to mean Hangzhou is “heaven on earth” China is located on the eastern part of the to the Chinese. Italian traveler Marco Polo in the Eurasian continent, west of the Pacific Ocean, 13th Century marveled at its beauty and riches. stretching 6200 kilometers (3720 miles) from east Hangzhou was one of the seven ancient capitals to west, 5500 kilometers (3300miles) from north of China. Since ancient times, scholars wrote to south. It is one of the largest countries spanning poetry to praise the beauty of the famous West 4 time zones with 9.6 million square kilometers Lake. It is well-known for its silk and “dragon land area, a population of 1.381 billion in 22 well” tea. Today, it is the headquarters of the e- provinces, 5 autonomous regions, 4 direct commerce giant Alibaba. Perhaps less well- controlled municipalities of Beijing, Tianjin, known is its connection with China’s Grand Shanghai and Chongqing, plus 2 self-governing Canal, the world’s earliest and longest man-made special regions of Hong Kong and Macau, and waterway running from Hangzhou to Beijing. sovereignty claims over Taiwan. The Grand Canal is another ancient mega-project on the scale of the Great Wall and it’s still in use Its diverse landscapes range from forest today. -

Accelerated Simulation of Chloride Ingress Into Concrete Under Dryingв
Construction and Building Materials 93 (2015) 205–213 Contents lists available at ScienceDirect Construction and Building Materials journal homepage: www.elsevier.com/locate/conbuildmat Accelerated simulation of chloride ingress into concrete under drying–wetting alternation condition chloride environment ⇑ Zhiwu Yu a,b, Ying Chen a,b, Peng Liu a,b,c, , Weilun Wang c a School of Civil Engineering, Central South University, 22 Shaoshan Road, Changsha 410075, China b National Engineering Laboratory for High Speed Railway Construction, Central South University, Changsha 410075, China c School of Civil Engineering, Shenzhen University, 3688 Nanhai Road, Shenzhen 518060, China highlights We investigate the chloride ingress into concrete under various environments. Acceleration factor is defined to represent environmental effect on chloride ingress. We propose the chloride diffusion coefficient model coupled with environment factors. Environmental conditions and concrete properties affect the acceleration factor. Numerical simulations and tests of chloride ingress are conducted. article info abstract Article history: In this study, the chloride diffusion coefficient model coupled with environmental factors is proposed to Received 6 April 2015 describe chloride ingress into concrete. The S curve model is also presented to fit the error function. Received in revised form 3 May 2015 Simultaneously, field test and artificial simulated environment experiments are conducted. Moreover, Accepted 11 May 2015 some typical RC structures are used as examples to investigate the application of the aforementioned models in forecasting service life. The results show that the chloride diffusion in concrete can be described by an equivalent chloride diffusion coefficient model proposed in this study, and the measured Keywords: data of chloride content in concrete correspond with the fitted profiles. -

The Shanghai Economic Sphere and Its Evolution As a Mega-Region
The Shanghai Economic Sphere and its Evolution as a Mega-Region —Geographical Expansion and the Rising Added Value of Shanghai— By Keiichiro Oizumi, Senior Economist Junya Sano, Senior Researcher Center for Pacific Business Studies Economics Department Japan Research Institute Summary 1. This article examines characteristics of economic development of the Shanghai economic sphere, which is defined as consisting of Shanghai Municipality, Jiangsu Province and Zhejiang Province. Income levels in this region are by far the highest in China. 2. With a population of 140 million, the Shanghai economic sphere has a gross re- gional product similar to that of South Korea. At over $5,000, the region’s per capita GRP is close to that of Malaysia. Development has been driven by export-based in- dustrialization. In 2007, the region’s exports were worth $482.0 billion, equivalent to 40% of the total exports of China. This is higher than the total for South Korea. Foreign-owned enterprises are the main driving force behind this performance. In 2007, foreign direct investment reached $40.2 billion. 3. Also significant is the region’s expansion as a consumer market. The Shanghai economic sphere accounts for approximately 20% of total retail sales in China. In urban areas, diffusion rates for televisions, washing machines, refrigerators and other electrical appliances have reached nearly 100%, and ownership of air conditioners, computers and mobile telephones is also rising. It is estimated that over 2 million households in the region have annual incomes in excess of $20,000. 4. Since the 1990s, the economic development of the Shanghai economic sphere has been accelerated by the active involvement of the central government in the de- velopment of the economic sphere, including the Pudong development in Shanghai, and by a continual influx of Japanese and Taiwanese companies in the area around Shanghai under the open-door policy.