And “Little Endian” Formats for Integers
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Institutionen För Datavetenskap Department of Computer and Information Science
Institutionen för datavetenskap Department of Computer and Information Science Final thesis NetworkPerf – A tool for the investigation of TCP/IP network performance at Saab Transpondertech by Magnus Johansson LIU-IDA/LITH-EX-A--09/039--SE 2009-08-13 Linköpings universitet Linköpings universitet SE-581 83 Linköping, Sweden 581 83 Linköping Final thesis NetworkPerf - A tool for the investigation of TCP/IP network performance at Saab Transpondertech Version 1.0.2 by Magnus Johansson LIU-IDA/LITH-EX-A09/039SE 2009-08-13 Supervisor: Hannes Persson, Attentec AB Examiner: Dr Juha Takkinen, IDA, Linköpings universitet Abstract In order to detect network changes and network troubles, Saab Transpon- dertech needs a tool that can make network measurements. The purpose of this thesis has been to nd measurable network proper- ties that best reect the status of a network, to nd methods to measure these properties and to implement these methods in one single tool. The resulting tool is called NetworkPerf and can measure the following network properties: availability, round-trip delay, delay variation, number of hops, intermediate hosts, available bandwidth, available ports, and maximum al- lowed packet size. The thesis also presents the methods used for measuring these properties in the tool: ping, traceroute, port scanning, and bandwidth measurement. iii iv Acknowledgments This master's thesis would not be half as good as it is, if I had not received help and support from several people. Many thanks to my examiner Dr Juha Takkinen, without whose countin- uous feedback this report would not have been more than a few confusing pages. -
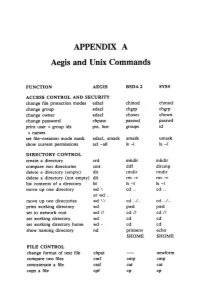
APPENDIX a Aegis and Unix Commands
APPENDIX A Aegis and Unix Commands FUNCTION AEGIS BSD4.2 SYSS ACCESS CONTROL AND SECURITY change file protection modes edacl chmod chmod change group edacl chgrp chgrp change owner edacl chown chown change password chpass passwd passwd print user + group ids pst, lusr groups id +names set file-creation mode mask edacl, umask umask umask show current permissions acl -all Is -I Is -I DIRECTORY CONTROL create a directory crd mkdir mkdir compare two directories cmt diff dircmp delete a directory (empty) dlt rmdir rmdir delete a directory (not empty) dlt rm -r rm -r list contents of a directory ld Is -I Is -I move up one directory wd \ cd .. cd .. or wd .. move up two directories wd \\ cd . ./ .. cd . ./ .. print working directory wd pwd pwd set to network root wd II cd II cd II set working directory wd cd cd set working directory home wd- cd cd show naming directory nd printenv echo $HOME $HOME FILE CONTROL change format of text file chpat newform compare two files emf cmp cmp concatenate a file catf cat cat copy a file cpf cp cp Using and Administering an Apollo Network 265 copy std input to std output tee tee tee + files create a (symbolic) link crl In -s In -s delete a file dlf rm rm maintain an archive a ref ar ar move a file mvf mv mv dump a file dmpf od od print checksum and block- salvol -a sum sum -count of file rename a file chn mv mv search a file for a pattern fpat grep grep search or reject lines cmsrf comm comm common to 2 sorted files translate characters tic tr tr SHELL SCRIPT TOOLS condition evaluation tools existf test test -

File Management Tools
File Management Tools ● gzip and gunzip ● tar ● find ● df and du ● od ● nm and strip ● sftp and scp Gzip and Gunzip ● The gzip utility compresses a specified list of files. After compressing each specified file, it renames it to have a “.gz” extension. ● General form. gzip [filename]* ● The gunzip utility uncompresses a specified list of files that had been previously compressed with gzip. ● General form. gunzip [filename]* Tar (38.2) ● Tar is a utility for creating and extracting archives. It was originally setup for archives on tape, but it now is mostly used for archives on disk. It is very useful for sending a set of files to someone over the network. Tar is also useful for making backups. ● General form. tar options filenames Commonly Used Tar Options c # insert files into a tar file f # use the name of the tar file that is specified v # output the name of each file as it is inserted into or # extracted from a tar file x # extract the files from a tar file Creating an Archive with Tar ● Below is the typical tar command used to create an archive from a set of files. Note that each specified filename can also be a directory. Tar will insert all files in that directory and any subdirectories. tar cvf tarfilename filenames ● Examples: tar cvf proj.tar proj # insert proj directory # files into proj.tar tar cvf code.tar *.c *.h # insert *.c and *.h files # into code.tar Extracting Files from a Tar Archive ● Below is the typical tar command used to extract the files from a tar archive. -

User's Manual
USER’S MANUAL USER’S > UniQTM UniQTM User’s Manual Ed.: 821003146 rev.H © 2016 Datalogic S.p.A. and its Group companies • All rights reserved. • Protected to the fullest extent under U.S. and international laws. • Copying or altering of this document is prohibited without express written consent from Datalogic S.p.A. • Datalogic and the Datalogic logo are registered trademarks of Datalogic S.p.A. in many countries, including the U.S. and the E.U. All other brand and product names mentioned herein are for identification purposes only and may be trademarks or registered trademarks of their respective owners. Datalogic shall not be liable for technical or editorial errors or omissions contained herein, nor for incidental or consequential damages resulting from the use of this material. Printed in Donnas (AO), Italy. ii SYMBOLS Symbols used in this manual along with their meaning are shown below. Symbols and signs are repeated within the chapters and/or sections and have the following meaning: Generic Warning: This symbol indicates the need to read the manual carefully or the necessity of an important maneuver or maintenance operation. Electricity Warning: This symbol indicates dangerous voltage associated with the laser product, or powerful enough to constitute an electrical risk. This symbol may also appear on the marking system at the risk area. Laser Warning: This symbol indicates the danger of exposure to visible or invisible laser radiation. This symbol may also appear on the marking system at the risk area. Fire Warning: This symbol indicates the danger of a fire when processing flammable materials. -
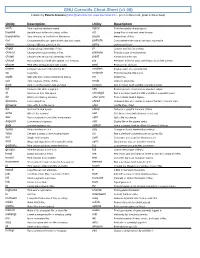
GNU Coreutils Cheat Sheet (V1.00) Created by Peteris Krumins ([email protected], -- Good Coders Code, Great Coders Reuse)
GNU Coreutils Cheat Sheet (v1.00) Created by Peteris Krumins ([email protected], www.catonmat.net -- good coders code, great coders reuse) Utility Description Utility Description arch Print machine hardware name nproc Print the number of processors base64 Base64 encode/decode strings or files od Dump files in octal and other formats basename Strip directory and suffix from file names paste Merge lines of files cat Concatenate files and print on the standard output pathchk Check whether file names are valid or portable chcon Change SELinux context of file pinky Lightweight finger chgrp Change group ownership of files pr Convert text files for printing chmod Change permission modes of files printenv Print all or part of environment chown Change user and group ownership of files printf Format and print data chroot Run command or shell with special root directory ptx Permuted index for GNU, with keywords in their context cksum Print CRC checksum and byte counts pwd Print current directory comm Compare two sorted files line by line readlink Display value of a symbolic link cp Copy files realpath Print the resolved file name csplit Split a file into context-determined pieces rm Delete files cut Remove parts of lines of files rmdir Remove directories date Print or set the system date and time runcon Run command with specified security context dd Convert a file while copying it seq Print sequence of numbers to standard output df Summarize free disk space setuidgid Run a command with the UID and GID of a specified user dir Briefly list directory -

You Can Download and Print the Meeting Schedule
EVERY WEEK DAY FRIDAY 6 PM SATURDAY NIGHT LIVE 7 PM HONOMU AS YET UNNAMED Serenity House, 15-2579 Pahoa-Keaau Rd., Pahoa ZOOM 5 PM WOMEN'S 11th STEP 8 AM ATTITUDE ADJUSTMENT NEW Hilo Coast United Church of Christ, Old Mamalahoa - O, BBS (near Pahoa Fire Station) MEDITATION -CL, WO LOCATION Onekahakaha Beach Park 74 Hwy. past the gym & turn left at the first driveway, https://zoom.us/j/400348959 Onekahakaha Rd, Hilo -OD, S, H Honomu - O, H ZOOM 6PM BEGINNER STEP MEETING psswd: 443670 https://us02web.zoom.us/j/4639358103?pwd 12 PM NOONERS now located at the Hilo soccer =c0FKRnJaVmNIQUlaS3lmRFVQNzZtdz09 field on Kamehameha Ave ***from Kilauea Ave turn TUESDAY 5:30 PM VOLCANO BIG BOOK GROUP psswd 9waxu4 East on Ponahawai Street. (toward the water) Right Cooper Center in Bookstore, Wright Rd., Volcano - on Bay Front (King Kamahemeha Ave) First drive ZOOM 7 PM SERENDIPITY -OD, H and CL, BB, H on right, at pavilion Bring Own Chair! 6:30 PM KEEP IT SIMPLE NEW Additional teleconference meeting Reflections https://us04web.zoom.us/j/9609522834 6 PM AA FRIDAY NIGHT Center for Spiritual Cooper Center on Wright Road, Volcano - Telephone number: 978-990-5000 Living, corner of 31st and Paradise in Hawaiian OD, H Access code: 226622 Paradise Park- OD, H ZOOM 7 PM ELEVATAH STAY BROKE Ask member for zoom info 7 PM YOUNG PEOPLES TUNDA 7 AM NANAWALE 4th DIMENSION (week 6 PM HILO MEN'S STAG 1842 Kino'ole St., Hilo O, 12 X 12 Lanakila Center, 600 Wailoa St. (across St. -

Unix Programmer's Manual
There is no warranty of merchantability nor any warranty of fitness for a particu!ar purpose nor any other warranty, either expressed or imp!ied, a’s to the accuracy of the enclosed m~=:crials or a~ Io ~helr ,~.ui~::~::.j!it’/ for ~ny p~rficu~ar pur~.~o~e. ~".-~--, ....-.re: " n~ I T~ ~hone Laaorator es 8ssumg$ no rO, p::::nS,-,,.:~:y ~or their use by the recipient. Furln=,, [: ’ La:::.c:,:e?o:,os ~:’urnes no ob~ja~tjon ~o furnish 6ny a~o,~,,..n~e at ~ny k:nd v,,hetsoever, or to furnish any additional jnformstjcn or documenta’tjon. UNIX PROGRAMMER’S MANUAL F~ifth ~ K. Thompson D. M. Ritchie June, 1974 Copyright:.©d972, 1973, 1974 Bell Telephone:Laboratories, Incorporated Copyright © 1972, 1973, 1974 Bell Telephone Laboratories, Incorporated This manual was set by a Graphic Systems photo- typesetter driven by the troff formatting program operating under the UNIX system. The text of the manual was prepared using the ed text editor. PREFACE to the Fifth Edition . The number of UNIX installations is now above 50, and many more are expected. None of these has exactly the same complement of hardware or software. Therefore, at any particular installa- tion, it is quite possible that this manual will give inappropriate information. The authors are grateful to L. L. Cherry, L. A. Dimino, R. C. Haight, S. C. Johnson, B. W. Ker- nighan, M. E. Lesk, and E. N. Pinson for their contributions to the system software, and to L. E. McMahon for software and for his contributions to this manual. -

USER MANUAL GWR High Speed Cellular Router Series
GWR USER MANUAL GWR High Speed Cellular Router Series Document version 1.0.0 Date: December 2015 WWW.GENEKO.RS User Manual Document History Date Description Author Comments 24.12.2015 User Manual Tanja Savić Firmware versions: 1.1.2 Document Approval The following report has been accepted and approved by the following: Signature Printed Name Title Date Dragan Marković Executive Director 24.12.2015 GWR High Speed Cellular Router Series 2 User Manual Content DOCUMENT APPROVAL ........................................................................................................................................ 2 LIST OF FIGURES .................................................................................................................................................... 5 LIST OF TABLES ...................................................................................................................................................... 8 DESCRIPTION OF THE GPRS/EDGE/HSPA ROUTER SERIES ...................................................................... 9 TYPICAL APPLICATION ............................................................................................................................... 10 TECHNICAL PARAMETERS ......................................................................................................................... 11 PROTOCOLS AND FEATURES ...................................................................................................................... 14 PRODUCT OVERVIEW ............................................................................................................................... -

Unix Commands (09/04/2014)
Unix Commands (09/04/2014) • Access control – login <login_name> – exit – passwd <login_name> – yppassswd <loginname> – su – • Login as Super user – su <login> • Login as user <login> • Root Prompt – [root@localhost ~] # • User Prompt – [bms@raxama ~] $ On Line Documentation – man <command/topic> – info <command/topic> • Working with directories – mkdir –p <subdir> ... {-p create all directories in path if not present} mkdir –p /2015/Jan/21/14 will create /2015, Jan, 21 & 14 in case any of these is absent – cd <dir> – rm -r <subdir> ... Man Pages • 1 Executable programs or shell commands • 2 System calls (functions provided by the kernel) • 3 Library calls (functions within program libraries) • 4 Special files (usually found in /dev) • 5 File formats and conventions eg /etc/passwd • 6 Games • 7 Miscellaneous (including macro packages and conventions), e.g. man(7), groff(7) • 8 System administration commands (usually only for root) • 9 Kernel routines [Non standard] – man grep, {awk,sed,find,cut,sort} – man –k mysql, man –k dhcp – man crontab ,man 5 crontab – man printf, man 3 printf – man read, man 2 read – man info Runlevels used by Fedora/RHS Refer /etc/inittab • 0 - halt (Do NOT set initdefault to this) • 1 - Single user mode • 2 - Multiuser, – without NFS (The same as 3, if you do not have networking) • 3 - Full multi user mode w/o X • 4 - unused • 5 - X11 • 6 - reboot (Do NOT set init default to this) – init 6 {Reboot System} – init 0 {Halt the System} – reboot {Requires Super User} – <ctrl> <alt> <del> • in tty[2-7] mode – tty switching • <ctrl> <alt> <F1-7> • In Fedora 10 tty1 is X. -

Gnu Coreutils Core GNU Utilities for Version 5.93, 2 November 2005
gnu Coreutils Core GNU utilities for version 5.93, 2 November 2005 David MacKenzie et al. This manual documents version 5.93 of the gnu core utilities, including the standard pro- grams for text and file manipulation. Copyright c 1994, 1995, 1996, 2000, 2001, 2002, 2003, 2004, 2005 Free Software Foundation, Inc. Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.1 or any later version published by the Free Software Foundation; with no Invariant Sections, with no Front-Cover Texts, and with no Back-Cover Texts. A copy of the license is included in the section entitled “GNU Free Documentation License”. Chapter 1: Introduction 1 1 Introduction This manual is a work in progress: many sections make no attempt to explain basic concepts in a way suitable for novices. Thus, if you are interested, please get involved in improving this manual. The entire gnu community will benefit. The gnu utilities documented here are mostly compatible with the POSIX standard. Please report bugs to [email protected]. Remember to include the version number, machine architecture, input files, and any other information needed to reproduce the bug: your input, what you expected, what you got, and why it is wrong. Diffs are welcome, but please include a description of the problem as well, since this is sometimes difficult to infer. See section “Bugs” in Using and Porting GNU CC. This manual was originally derived from the Unix man pages in the distributions, which were written by David MacKenzie and updated by Jim Meyering. -

US EPA, Pesticide Product Label, Orondis OD,10/05/2017
81,7('67$7(6(19,5210(17$/3527(&7,21$*(1&< :$6+,1*721'& 2)),&(2)&+(0,&$/6$)(7< $1'32//87,2135(9(17,21 2FWREHU 0V+HLGL%,UULJ 5HJXODWRU\5HVLGXH0DQDJHU 6\QJHQWD&URS3URWHFWLRQ//& 32%R[ *UHHQVERUR1& 6XEMHFW 35,$/DEHO$PHQGPHQW±QHZXVHIRUFDFDRDGGVVXSSOHPHQWDOODEHOIRUFDFDR DVVRFLDWHG3HWLWLRQ( 3URGXFW1DPH2URQGLV2' (3$5HJLVWUDWLRQ1XPEHU $SSOLFDWLRQ'DWH 'HFLVLRQ1XPEHU 'HDU0V,UULJ 7KHDSSOLFDWLRQUHIHUUHGWRDERYHVXEPLWWHGXQGHUWKH)HGHUDO,QVHFWLFLGH)XQJLFLGHDQG 5RGHQWLFLGH$FWDVDPHQGHGLVDFFHSWDEOHXQGHU),)5$VHF F <RXPXVWVXEPLWDQGRU FLWHDOOGDWDUHTXLUHGIRUUHJLVWUDWLRQUHUHJLVWUDWLRQUHJLVWUDWLRQUHYLHZRI\RXUSURGXFWZKHQWKH $JHQF\UHTXLUHVDOOUHJLVWUDQWVRIVLPLODUSURGXFWVWRVXEPLWVXFKGDWD $VWDPSHGFRS\RI\RXU0DVWHUDQG6XSSOHPHQWDOODEHOLQJDUHHQFORVHGIRU\RXUUHFRUGV7KLV ODEHOLQJVXSHUVHGHVDOOSUHYLRXVO\DFFHSWHGODEHOLQJ<RXPXVWVXEPLWRQH FRS\RIWKHILQDO SULQWHGODEHOLQJEHIRUH\RXUHOHDVHWKHSURGXFWIRUVKLSPHQWZLWKWKHQHZODEHOLQJ,QDFFRUGDQFH ZLWK&)5 F \RXPD\GLVWULEXWHRUVHOOWKLVSURGXFWXQGHUWKHSUHYLRXVO\DSSURYHG ODEHOLQJIRUPRQWKVIURPWKHGDWHRIWKLVOHWWHU$IWHUPRQWKV\RXPD\RQO\GLVWULEXWHRU VHOOWKLVSURGXFWLILWEHDUVWKLVQHZUHYLVHGODEHOLQJRUVXEVHTXHQWO\DSSURYHGODEHOLQJ³7R GLVWULEXWHRUVHOO´LVGHILQHGXQGHU),)5$VHFWLRQ JJ DQGLWVLPSOHPHQWLQJUHJXODWLRQDW &)5 6KRXOG\RXZLVKWRDGGUHWDLQDUHIHUHQFHWRWKHFRPSDQ\¶VZHEVLWHRQ\RXUODEHOWKHQSOHDVHEH DZDUHWKDWWKHZHEVLWHEHFRPHVODEHOLQJXQGHUWKH)HGHUDO,QVHFWLFLGH)XQJLFLGHDQG5RGHQWLFLGH $FWDQGLVVXEMHFWWRUHYLHZE\WKH$JHQF\,IWKHZHEVLWHLVIDOVHRUPLVOHDGLQJWKHSURGXFW ZRXOGEHPLVEUDQGHGDQGXQODZIXOWRVHOORUGLVWULEXWHXQGHU),)5$VHFWLRQ D ( &)5 D OLVWH[DPSOHVRIVWDWHPHQWV(3$PD\FRQVLGHUIDOVHRUPLVOHDGLQJ,QDGGLWLRQ -

Intro to Unix 2018
Introduction to *nix Bill Renaud, OLCF ORNL is managed by UT-Battelle for the US Department of Energy Background • UNIX operating system was developed in 1969 by Ken Thompson and Dennis Ritchie • Many “UNIX-like” OSes developed over the years • UNIX® is now a trademark of The Open Group, which maintains the Single UNIX Specification • Linux developed by Linus Torvalds in 1991 • GNU Project started by Richard Stallman in 1983 w/aim to provide free, UNIX-compatible OS • Many of the world’s most powerful computers use Linux kernel + software from the GNU Project References: 1www.opengroup.org/unix 2https://en.wikipedia.org/wiki/Linux 2 3https://www.gnu.org/gnu/about-gnu.html This Presentation • This presentation will focus on using *nix operating systems as a non-privileged user in an HPC environment – Assumes you’re using a ‘remote’ system – No info on printing, mounting disks, etc. • We’ll focus on systems using the Linux kernel + system software from the GNU project since that’s so prevalent • Two-Part – Basics: general information, commands – Advanced: advanced commands, putting it all together, scripts, etc. 3 This Presentation • May seem a bit disjoint at first – Several basic concepts that don’t flow naturally but later topics build upon – Hopefully everything will come together, but if not… • I’ll cover (what I hope is) some useful info but can’t cover it all – People write thousand-page books on this, after all • Please ask questions! 4 Basics Terminology • User – An entity that interacts with the computer. Typically a person but could also be for an automated task.