Seasonal Sea Level Outlook and Reducing Vulnerability to Coastal Hazards—The Experience of the ‘Pacific ENSO Applications Center’
Total Page:16
File Type:pdf, Size:1020Kb
Load more
Recommended publications
-

Strategic Plan 2021-2025
Strategic Plan 2021-2025 Map of FSM 2 Contents Map of FSM ___________________________________________________________________________________________________________________ 2 Key Issues in the FSM________________________________________________________________________________________________________ 4 Country Context _____________________________________________________________________________________________________________ 7 Major Vulnerability and Hazards Analysis _________________________________________________________________________________ 8 History of Micronesia Red Cross Society (MRCS) __________________________________________________________________________ 9 IFRC Strategy 2030 _________________________________________________________________________________________________________ 11 MRCS Vision _________________________________________________________________________________________________________________ 12 MRCS Mission: ______________________________________________________________________________________________________________ 12 Strategic Aims 2021-2025 _________________________________________________________________________________________________ 13 Strategic Aim 1: Save lives in times of disasters and crises ______________________________________________________________ 14 Strategic Aim 2: Enable healthy and safe living ___________________________________________________________________________ 16 Strategic Aim 3: Promote the prevention and reduction of vulnerability, social inclusion and a culture of non- violence -
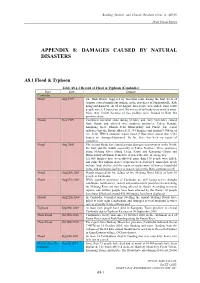
Appendix 8: Damages Caused by Natural Disasters
Building Disaster and Climate Resilient Cities in ASEAN Draft Finnal Report APPENDIX 8: DAMAGES CAUSED BY NATURAL DISASTERS A8.1 Flood & Typhoon Table A8.1.1 Record of Flood & Typhoon (Cambodia) Place Date Damage Cambodia Flood Aug 1999 The flash floods, triggered by torrential rains during the first week of August, caused significant damage in the provinces of Sihanoukville, Koh Kong and Kam Pot. As of 10 August, four people were killed, some 8,000 people were left homeless, and 200 meters of railroads were washed away. More than 12,000 hectares of rice paddies were flooded in Kam Pot province alone. Floods Nov 1999 Continued torrential rains during October and early November caused flash floods and affected five southern provinces: Takeo, Kandal, Kampong Speu, Phnom Penh Municipality and Pursat. The report indicates that the floods affected 21,334 families and around 9,900 ha of rice field. IFRC's situation report dated 9 November stated that 3,561 houses are damaged/destroyed. So far, there has been no report of casualties. Flood Aug 2000 The second floods has caused serious damages on provinces in the North, the East and the South, especially in Takeo Province. Three provinces along Mekong River (Stung Treng, Kratie and Kompong Cham) and Municipality of Phnom Penh have declared the state of emergency. 121,000 families have been affected, more than 170 people were killed, and some $10 million in rice crops has been destroyed. Immediate needs include food, shelter, and the repair or replacement of homes, household items, and sanitation facilities as water levels in the Delta continue to fall. -

MASARYK UNIVERSITY BRNO Diploma Thesis
MASARYK UNIVERSITY BRNO FACULTY OF EDUCATION Diploma thesis Brno 2018 Supervisor: Author: doc. Mgr. Martin Adam, Ph.D. Bc. Lukáš Opavský MASARYK UNIVERSITY BRNO FACULTY OF EDUCATION DEPARTMENT OF ENGLISH LANGUAGE AND LITERATURE Presentation Sentences in Wikipedia: FSP Analysis Diploma thesis Brno 2018 Supervisor: Author: doc. Mgr. Martin Adam, Ph.D. Bc. Lukáš Opavský Declaration I declare that I have worked on this thesis independently, using only the primary and secondary sources listed in the bibliography. I agree with the placing of this thesis in the library of the Faculty of Education at the Masaryk University and with the access for academic purposes. Brno, 30th March 2018 …………………………………………. Bc. Lukáš Opavský Acknowledgements I would like to thank my supervisor, doc. Mgr. Martin Adam, Ph.D. for his kind help and constant guidance throughout my work. Bc. Lukáš Opavský OPAVSKÝ, Lukáš. Presentation Sentences in Wikipedia: FSP Analysis; Diploma Thesis. Brno: Masaryk University, Faculty of Education, English Language and Literature Department, 2018. XX p. Supervisor: doc. Mgr. Martin Adam, Ph.D. Annotation The purpose of this thesis is an analysis of a corpus comprising of opening sentences of articles collected from the online encyclopaedia Wikipedia. Four different quality categories from Wikipedia were chosen, from the total amount of eight, to ensure gathering of a representative sample, for each category there are fifty sentences, the total amount of the sentences altogether is, therefore, two hundred. The sentences will be analysed according to the Firabsian theory of functional sentence perspective in order to discriminate differences both between the quality categories and also within the categories. -

Tropical Cyclones 2019
<< LINGLING TRACKS OF TROPICAL CYCLONES IN 2019 SEP (), !"#$%&'( ) KROSA AUG @QY HAGIBIS *+ FRANCISCO OCT FAXAI AUG SEP DANAS JUL ? MITAG LEKIMA OCT => AUG TAPAH SEP NARI JUL BUALOI SEPAT OCT JUN SEPAT(1903) JUN HALONG NOV Z[ NEOGURI OCT ab ,- de BAILU FENGSHEN FUNG-WONG AUG NOV NOV PEIPAH SEP Hong Kong => TAPAH (1917) SEP NARI(190 6 ) MUN JUL JUL Z[ NEOGURI (1920) FRANCISCO (1908) :; OCT AUG WIPHA KAJIK() 1914 LEKIMA() 1909 AUG SEP AUG WUTIP *+ MUN(1904) WIPHA(1907) FEB FAXAI(1915) JUL JUL DANAS(190 5 ) de SEP :; JUL KROSA (1910) FUNG-WONG (1927) ./ KAJIKI AUG @QY @c NOV PODUL SEP HAGIBIS() 1919 << ,- AUG > KALMAEGI OCT PHANFONE NOV LINGLING() 1913 BAILU()19 11 \]^ ./ ab SEP AUG DEC FENGSHEN (1925) MATMO PODUL() 191 2 PEIPAH (1916) OCT _` AUG NOV ? SEP HALONG (1923) NAKRI (1924) @c MITAG(1918) NOV NOV _` KALMAEGI (1926) SEP NAKRI KAMMURI NOV NOV DEC \]^ MATMO (1922) OCT BUALOI (1921) KAMMURI (1928) OCT NOV > PHANFONE (1929) DEC WUTIP( 1902) FEB 二零一 九 年 熱帶氣旋 TROPICAL CYCLONES IN 2019 2 二零二零年七月出版 Published July 2020 香港天文台編製 香港九龍彌敦道134A Prepared by: Hong Kong Observatory 134A Nathan Road Kowloon, Hong Kong © 版權所有。未經香港天文台台長同意,不得翻印本刊物任何部分內容。 © Copyright reserved. No part of this publication may be reproduced without the permission of the Director of the Hong Kong Observatory. 本刊物的編製和發表,目的是促進資 This publication is prepared and disseminated in the interest of promoting 料交流。香港特別行政區政府(包括其 the exchange of information. The 僱員及代理人)對於本刊物所載資料 Government of the Hong Kong Special 的準確性、完整性或效用,概不作出 Administrative Region -

State of the Climate in 2015
STATE OF THE CLIMATE IN 2015 Special Supplement to the Bulletin of the American Meteorological Society Vol. 97, No. 8, August 2016 STATE OF THE CLIMATE IN 2015 Editors Jessica Blunden Derek S. Arndt Chapter Editors Howard J. Diamond Jeremy T. Mathis Jacqueline A. Richter-Menge A. Johannes Dolman Ademe Mekonnen Ahira Sánchez-Lugo Robert J. H. Dunn A. Rost Parsons Carl J. Schreck III Dale F. Hurst James A. Renwick Sharon Stammerjohn Gregory C. Johnson Kate M. Willett Technical Editors Kristin Gilbert Tom Maycock Susan Osborne Mara Sprain AMERICAN METEOROLOGICAL SOCIETY COVER CREDITS: FRONT: Reproduced by courtesy of Jillian Pelto Art/University of Maine Alumnus, Studio Art and Earth Science — Landscape of Change © 2015 by the artist. BACK: Reproduced by courtesy of Jillian Pelto Art/University of Maine Alumnus, Studio Art and Earth Science — Salmon Population Decline © 2015 by the artist. Landscape of Change uses data about sea level rise, glacier volume decline, increasing global temperatures, and the increas- ing use of fossil fuels. These data lines compose a landscape shaped by the changing climate, a world in which we are now living. (Data sources available at www.jillpelto.com/landscape-of-change; 2015.) Salmon Population Decline uses population data about the Coho species in the Puget Sound, Washington. Seeing the rivers and reservoirs in western Washington looking so barren was frightening; the snowpack in the mountains and on the glaciers supplies a lot of the water for this region, and the additional lack of precipitation has greatly depleted the state’s hydrosphere. Consequently, the water level in the rivers the salmon spawn in is very low, and not cold enough for them. -

Appendix 3 Selection of Candidate Cities for Demonstration Project
Building Disaster and Climate Resilient Cities in ASEAN Final Report APPENDIX 3 SELECTION OF CANDIDATE CITIES FOR DEMONSTRATION PROJECT Table A3-1 Long List Cities (No.1-No.62: “abc” city name order) Source: JICA Project Team NIPPON KOEI CO.,LTD. PAC ET C ORP. EIGHT-JAPAN ENGINEERING CONSULTANTS INC. A3-1 Building Disaster and Climate Resilient Cities in ASEAN Final Report Table A3-2 Long List Cities (No.63-No.124: “abc” city name order) Source: JICA Project Team NIPPON KOEI CO.,LTD. PAC ET C ORP. EIGHT-JAPAN ENGINEERING CONSULTANTS INC. A3-2 Building Disaster and Climate Resilient Cities in ASEAN Final Report Table A3-3 Long List Cities (No.125-No.186: “abc” city name order) Source: JICA Project Team NIPPON KOEI CO.,LTD. PAC ET C ORP. EIGHT-JAPAN ENGINEERING CONSULTANTS INC. A3-3 Building Disaster and Climate Resilient Cities in ASEAN Final Report Table A3-4 Long List Cities (No.187-No.248: “abc” city name order) Source: JICA Project Team NIPPON KOEI CO.,LTD. PAC ET C ORP. EIGHT-JAPAN ENGINEERING CONSULTANTS INC. A3-4 Building Disaster and Climate Resilient Cities in ASEAN Final Report Table A3-5 Long List Cities (No.249-No.310: “abc” city name order) Source: JICA Project Team NIPPON KOEI CO.,LTD. PAC ET C ORP. EIGHT-JAPAN ENGINEERING CONSULTANTS INC. A3-5 Building Disaster and Climate Resilient Cities in ASEAN Final Report Table A3-6 Long List Cities (No.311-No.372: “abc” city name order) Source: JICA Project Team NIPPON KOEI CO.,LTD. PAC ET C ORP. -

FEDERATED STATES of MICRONESIA Disaster Management Reference Handbook
FEDERATED STATES OF MICRONESIA Disaster Management Reference Handbook November 2019 Acknowledgements CFE-DM would like to thank the following organizations for their support in reviewing and providing feedback to this document: Tiare Eastmond, Regional Advisor-Pacfic, USAID/OFDA John Paul Henderson, Regional Counsel, FEMA Region IX Stan Keolanui, Plans Analyst, U.S. Army Pacific Robert Pierce, USAID/Philippines & Pacific/Environment Colby Stanton, FEMA LTC John T. Yoshimori, 9th MSC Oceania Planner, U.S. Army Pacific Cover and section photo credits Cover Photo: “View from Sokehs Rock” (Pohnpei, Federated States of Micronesia) by Vagabond Travel Tales is licensed under CC BY-NC-SA 2.0. March 12, 2008. https://www.flickr.com/photos/122663252@N02/13744706023 Map Cover: Full political map of Micronesia. 2011. Vidiani.com maps of the world. http://www.vidiani.com/full-political-map-of-micronesia/ Country Overview Section Photo: “Yap Dancers” by Dana Lee Craker is licensed under CC BY-NC-ND 2.0. April 1, 2008. https://www.flickr.com/photos/32975809@N00/47932607727 Disaster Overview Section Photo: “110703-O-ZZ999-004” by Kristopher Radder (U.S. Pacific Fleet) is licensed under CC BY-SA 2.0. An MH-60S Sea Hawk flies over the port of Pohnpei, Federated States of Micronesia for Pacific Partnership 2011. https://www.flickr.com/photos/compacflt/5895999601/in/faves-63479458@N04/ Organizational Structure for Disaster Management Photo: “161211-N-YM720-059” by COMSEVENTHFLT is licensed under CC BY-SA 2.0. Loadmasters attached to the 36th Airlift Squadron, Yokota Air Base, Japan, drop care packages out of a C-130H Hercules to a Micronesian island during Operation Christmas Drop, an international humanitarian operation (U.S. -
![MEMBER REPORT [Republic of Korea]](https://docslib.b-cdn.net/cover/0897/member-report-republic-of-korea-3540897.webp)
MEMBER REPORT [Republic of Korea]
MEMBER REPORT [Republic of Korea] ESCAP/WMO Typhoon Committee 14th Integrated Workshop Guam, USA 4 – 7 November 2019 CONTENTS I. Overview of tropical cyclones which have affected/impacted Member’s area since the last Committee Session 1. Meteorological Assessment 2. Hydrological Assessment 3. Socio-Economic Assessment II. Summary of Progress in Priorities supporting Key Result Areas 1. The Web-based Portal to Provide Products of Seasonal Typhoon Activity Outlook for TC Members (POP1) 2. Technology Transfer of Typhoon Operation System (TOS) to the Macao Meteorological and Geophysical Bureau (POP4) 3. 2019 TRCG Research Fellowship Scheme by KMA 4. Co-Hosted the 12th Korea-China Joint Workshop on Tropical Cyclones 5. Improved KMA’s Typhoon Intensity Classification 6. Operational Service of GEO-KOMPSAT-2A 7. Developing Typhoon Analysis Technique for GEO-KOMPSAT-2A 8. Preliminary Research on Establishment of Hydrological Data Quality Control in TC Members 9. Task Improvement to Increase Effects in Flood Forecasting 10. Enhancement of Flood Forecasting Reliability with Radar Rainfall Data 11. Flood Risk Mapping of Korea 12. Expert Mission 13. Setting up Early Warning and Alert System in Lao PDR and Vietnam 14. The 14th Annual Meeting of Typhoon Committee Working Group on Disaster Risk Reduction 15. Sharing Information Related to DRR I. Overview of tropical cyclones which have affected/impacted Member’s area since the last Committee Session 1. Meteorological Assessment (highlighting forecasting issues/impacts) Twenty typhoons have occurred up until 18 October 2019 in the western North Pacific basin. The number of typhoons in 2019 was below normal, compared to the 30-year (1981-2010) average number of occurrences (25.6). -

A Quarterly Bulletin of the Pacific El Nino/Southern Oscillation Applications Center (PEAC) Providing Information on Climate
2nd Quarter, 2007 Vol. 13, No. 2 ISSUED: APRIL 26, 2007 A Quarterly Bulletin of the Pacific El Nino/Southern Oscillation Applications Center (PEAC) Providing Information on Climate Variability for the U.S.-Affiliated Pacific Islands www.soest.hawaii.edu/MET/Enso CURRENT CONDITIONS El Niño conditions in the ocean abruptly ended at the tion of rainfall is anticipated for the next three months. Rainfall beginning of February 2007, and oceanic and atmospheric forecasts issued by NOAA’s Climate Prediction Center for Ha- circulation patterns are now in an ENSO-neutral state. waii give equal chances of below average, near average, or Some of the islands in the RMI, Chuuk State, and Guam have above average rainfall through early summer . experienced very dry conditions for some or all of the past three Sea-level variation in the USAPI is sensitive to ENSO- months. Three-month rainfall totals were less than half of nor- cycle, with low sea-level observed during El Niño and high sea- mal at some locations in the northern RMI (see figures 1a, 1b). level during La Niña years. Consistent with the transition from Other island groups have had adequate to abundant rainfall. ENSO-neutral to La Niña conditions, observations reveal that Three-month rainfall totals exceeded 125% of normal at some the sea level has already started to record a rise this year as most locations in Chuuk State, Pohnpei State, American Samoa, and locations across the USAPI have recorded moderate positive (surprisingly) Saipan. The 51.67 inches of rainfall at American deviations. Samoa during the first three months of 2007 was the highest The following comments from the EL NIÑO/SOUTHERN recorded value in the USAPI, followed closely by the just-over OSCILLATION (ENSO) DIAGNOSTIC DISCUSSION were 50 inches recorded in the same time period at Nukuoro in posted on the U.S. -

A Quarterly Bulletin of the Pacific El Niño/Southern Oscillation
2nd Quarter, 2009 Vol. 15, No. 2 ISSUED: April 30, 2009 A Quarterly Bulletin of the Pacific El Niño/Southern Oscillation Applications Climate (PEAC) Center Providing Information on Climate Variability for the U.S.-Affiliated Pacific Islands www.soest.hawaii.edu/MET/Enso CURRENT CONDITIONS According to the U.S. Climate Prediction Center (CPC), high sea level observed during La Niña events. Sea levels have the present oceanic and atmospheric anomalies indicate an been higher than average in the Pacific since early 2007. Cur- ongoing transition from La Niña to ENSO-neutral. Precipita- rent forecasts indicate that sea level across the USAPI will tion and surface wind anomalies in the tropical Pacific have re- remain elevated 2-6 inches above normal for the next 3 flected La Niña for the past several months, characterized by a months, while sea level at Hawaiian stations is expected to westward retraction of deep tropical convection toward Indone- remain near normal. sia, suppressed precipitation centered on the Date Line, and en- The following comments were taken from WFO Guam’s hanced easterly winds across most of Micronesia. The weather MONTHLY PACIFIC ENSO DISCUSSION FOR MICRONE- across the USAPI has remained tranquil, with no extremes of SIA AND AMERICAN SAMOA, issued in April 2009: high wind and few extremes of heavy rain. For the past two “While sea surface temperatures (SSTs) remained cooler than months, persistent dry conditions have threatened the water re- normal in the eastern and east-central equatorial Pacific, they sources of some atolls in the RMI. The most troublesome aspect continued to exhibit warming throughout the month. -

Yap Joint State Action Plan for Disaster Risk Management and Climate Change
Federated States of Micronesia Federated States of Micronesia Federated States of Micronesia Yap Joint State Action Plan for Disaster Risk Management and Climate Change Yap Joint State Action Plan for Disaster Risk Management and Climate Change Yap Joint State Action Plan for Disaster Risk Management and Climate Change a Federated States of Micronesia Yap Joint State Action Plan for Disaster Risk Management and Climate Change i Federated States of Micronesia ©Copyright Secretariat of the Pacific Community (SPC) 2015 All rights for commercial/for profit reproduction or translation, in any form, reserved. SPC authorises the partial reproduction or translation of this material for scientific, educational or research purposes, provided that SPC and the source document are properly acknowledged. Permission to reproduce the document and/or translate in whole, in any form, whether for commercial/for profit or non- profit purposes, must be requested in writing. Original SPC artwork may not be altered or separately published without permission. Original text: English Secretariat of the Pacific Community cataloguing-in-publication data ii Yap Joint State Action Plan for Disaster Risk Management and Climate Change Federated States of Micronesia Federated States of Micronesia FOREWORD Yap State has been experiencing the impacts of climate change related disasters more than any of the three other states in the Federated States of Micronesia. The patterns of typhoons are changing, bringing uncertainty regarding local impacts such as heavy rainfall and storm surges which affect the fragile environment that has sustained our past generations. Our strong social and cultural systems, which have been an important source of our resilience, is under immense pressure, partly due to increased frequency and magnitude climate change impacts and climate variability events, thus contributing to accelerated resource depletion, as seen in various sectors in Yap. -

JP4.10 Normalized Radar Cross-Section (NRCS) Patterns From
JP4.10 Normalized radar cross-section (NRCS) patterns from QuikSCAT-A new analysis tool over the tropical oceans Roger T. Edson, Anteon Corporation, University of Guam (WERI), Mangilao, Guam and Paul S. Chang, NOAA/NESDIS/ORA, Camp Spring MD 1. INTRODUCTION The process takes advantage of the ‘slice’ data which are retrieved by the commandable variable range This paper examines meteorological features and processor onboard QuikSCAT and which subdivides surface wind patterns over the tropical oceans as the original 25-km by 37-km microwave footprint into depicted in high resolution Normalized Radar Cross- 2- to 10-km ‘slices’ (Perry 2000). The data are Section (NRCS) imagery. The NRCS are derived normally stored as part of the Level 2A SeaWinds from the high resolution slice data obtained from the data base at the JPL, Physical Oceanography SeaWinds scatterometer onboard the QuikSCAT Distribution Active Archive Center (PO.DAAC). The satellite. As is the case for all scatterometry data, the method used in this display, takes the near real time NRCS images are a reflection of the backscattered slice data and processes it through a smoothing microwave energy from small centimeter length routine which takes up to eight overlapping slices capillary waves on the ocean surface. In a process over a 3 km grid to create an image in dB of varying known as Bragg Scattering, this energy is highly gray shades and with an effective resolution of 6 km. correlated to the roughness of the ocean surface as The NOAA/NESDIS TC Storm web page then remaps determined by the instantaneous wind field.