DOCSLIB.ORG

Kramers' Theory of Reaction Kinetics

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Kramers' Theory of Reaction Kinetics Kramers’ Theory of Reaction Kinetics In this lab module, you will learn about why a chemical reaction occurs with a particular rate and how it relates to the chemical reaction barrier. At the lowest level of theory (aka Freshman Chemistry), you learned the rate of a chemical reaction can be calculated using the Arrhenius equation: * G kBT k Ae (1) * where A is the pre-exponential, G is the activation energy, kB is the Boltzmann constant, and T is the temperature. There are a few problems with this equation, namely what is the pre- exponential A? The first attempt to define it comes from Transition State Theory (TST), which describes two chemical species with enough energy to cross a single energy barrier to a new state (i.e. a chemical reaction has occurred). Transition State Theory also stipulates that the chemicals cannot react “backwards” to reform the original reactants. Using TST, the Arrhenius equation is transformed into: * G k T k T k B e B h (2) where h is Plank’s constant. While TST is a good improvement over the empirical Arrhenius equation, there are still several significant problems. For one, it doesn’t seem to work well except for a few cases. One obvious shortcoming is the idea that when chemicals have enough energy, they will always react (and never go “backwards”, which really not correct). Here is a way to “fix” the TST result: * k T G k B e kB T h (3) The function of is very interesting; it is called the transmission coefficient. It is a unit-less percentage that defines how many molecules will react, form a product (and stay that way) if they have enough energy. You may notice that, if I calculate a TST rate which doesn’t match the experiment, I can just calculate a that “fixes” it. This in my opinion is cheating. Scientists began to analyze how to determine from basic physical principals as opposed to empirical observations. The first question to ask, how does the solvent affect the transmission coefficient? Isn’t it sensible that a reaction will occur faster in water than in molasses? What about a reaction in the gas phase, where there is no solvent rather than a buffer gas that occasionally bumps into the reactants? To test your assumptions, we will examine the simplest scenario possible- the reaction of A and B to form C in the gas phase. Shown here are A and B in their potential energy surface (PES), which is defined the function U(x). We will call “x” the reaction coordinate; it doesn’t really represent Cartesian space rather than measure how much A and B are more like reactants or whether they have become products. The PES contains two wells, one for the reactants and one for the product. There is a simple energy barrier from one to the other. Let’s say that a flash of light strikes A and B to impart enough energy for them to cross the barrier to form C as shown here: Note- there is a small problem: if the molecules have enough energy to cross the barrier from reactant to product, then they have enough energy to react backwards as well: It seems that molecules A and B are stuck; after all, the law of constant energy means that they will be able to wander over the energy hill forever. Without a way to lose the energy that we gave them, A and B as just going to wander over the reactant and product wells continuously; this makes the transmission coefficient =0. In this case, it is sensible to ask how can anything ever reactant form products? First, examine some unspoken assumptions; such as, is there anything else in the entire universe but A and B? No, while this reaction is occurring in outer space, there are still some gas molecules floating around nearby. In our hypothetical situation, a buffer gas molecule may strike A and B when they happen to be hovering over the product basin. The gas molecule ends up taking energy out of A and B such that they can now drop into the product state to form C. It seems that having some buffer gas around is “helpful” in terms of this reaction occurring. Under these conditions (called the Kramers Low Viscosity Regime), the transmission coefficient (and thus the overall reaction rate) increase linearly with solvent viscosity. Now let’s take things to another extreme, A and B are in a very dense, thick liquid. They have enough energy to react, but the other molecules (the solvent or buffer gas) present a physical barrier for the reaction to occur. This process is illustrated here: The solvent or buffer gas can slow the reaction down in many ways; for one, they can simply get in-between A and B preventing them from physically making contact. They can also slow down the diffusion of A and B such that it takes longer for them to “touch” each other and react. The solvent interacts so strongly with A and B that it may take away all their energy before they can cross the barrier. Furthermore, once A and B do connect, there may be some spatial rearrangements of the atoms that comprise molecules A and B to from C that the solvent molecules are opposing. This case is called the Kramers High Friction Regime; under these circumstances the transmission coefficient (and thus rate of reaction) is inversely proportional to the solvent viscosity. The sum of these examples illustrates that the rate of a reaction is controlled by a lot more than the activation energy barrier G*. The pre-exponential has a strong effect, which is largely dictated by the nature of the medium that the reaction is occurring in. The local environment can do this by affecting the transmission coefficient . If we can define , then we may finally understand why a chemical reaction appears to occur at the rate that the scientist measures. Hendrik Kramers studied this theoretical problem in 1940 using Langevin dynamics via the Langevin Equation. The Langevin equation is: 2 x U(x) x m 2 m f (t) t x t (4) where m is mass of the chemicals that are reacting, x represents the reaction coordinate on a potential energy surface defined by U(x), is the solvent viscosity, and f(t) is a force that randomly knocks things around; f(t) is due to the solvent impacting the chemicals (this is where Brownian motion comes from). In the Langevin equation, the presence of a buffer gas or a solvent is represented by the presence of viscosity that slows down anything moving (this is why x it is multiplied by the velocity . If something isn’t moving, then the viscosity of the solvent t doesn’t do anything to it). This viscous “drag” on the reactants is compensated by the random force f(t) that gets them moving again. Kramers performed very sophisticated mathematical operations on the Langevin equation and solved for the transmission coefficient as a function of solvent viscosity. The result was so confusing to researchers that Kramer’s work was ignored for some time (no one else was smart enough to follow the math). Here is what Kramers calculated for the overall rate of a chemical reaction: 1 2 2 * G R 2B m kB T k 1 1e (5) 4 B m where R and B are related to the curvature of the potential energy surface in the vicinity of the reactants and barrier, respectively. We are fortunate that Equation 5 has two solutions in limiting regimes. For very high viscosity (large ), eq. 5 can be recast as: * G m k T k R B e B (6) 2 Note how the rate goes down with solvent viscosity as stated previously. The rate equation in the limiting regime where is very small is a bit more complicated, but it shows that the rate is linearly proportional to the viscosity. Reaction Kinetics In this laboratory exercise, you will study the effect of solvent viscosity on a reaction using transient absorption spectroscopy. Specifically, the light-initiated reaction of benzophenone as described here is examined. When benzophenone (C6H5)2CO absorbs a UV/Visible photon, it is excited to its first electronic state and quickly intersystem crosses to the triplet state: (C6H5)2CO + h → (C6H5)2CO* (S1) → (C6H5)2CO* (T1) (7) In an alcohol solvent, a proton is abstracted from the alcohol to form a protonated ketyl radical: • • (C6H5)2CO* (T1) + ROH → (C6H5)2COH + ROH (8) In the presence of potassium hydroxide, the protonated ketyl radicals can disassociate: KD • •- + (C6H5)2COH ↔ (C6H5)2CO + H (9) Note that the protonated neutral radical and deprotonated anion radical are in equilibrium and KD is an equilibrium constant. Finally, the protonated and deprotonated forms of the ketyl radicals can dimerize, forming the benzopinacol anion: k • •- - (C6H5)2COH + (C6H5)2CO → (C6H5)2(OH)C-C(O )(C6H5)2 (10) where a new bond is formed between the carbon atoms. This is the reaction your measuring! We will be probing the rate of decay of the deprotonated ketyl radical anion can be deduced from the above equation to be overall a second order process: (C6H5 )2 CO k (C6H5 )2 COH (C6H5 )2 CO (11) t If we assume that protonated and deprotonated forms of the ketyl radicals rapidly reaches equilibrium with an equilibrium constant of KD, then its equilibrium relationship can be rearranged to yield • •- + [(C6H5)2COH ] = [(C6H5)2CO ][H ]/ KD (12) Now substituting (12) into (11) into yields: 2 (C6H5 )2 CO kobs (C6H5 )2 CO (13) t + where kobs = k[H ]/KD.
Load more

Recommended publications
  • Chapter 12 Lecture Notes
    Chemical Kinetics “The study of speeds of reactions and the nanoscale pathways or rearrangements by which atoms and molecules are transformed to products” Chapter 13: Chemical Kinetics: Rates of Reactions © 2008 Brooks/Cole 1 © 2008 Brooks/Cole 2 Reaction Rate Reaction Rate Combustion of Fe(s) powder: © 2008 Brooks/Cole 3 © 2008 Brooks/Cole 4 Reaction Rate Reaction Rate + Change in [reactant] or [product] per unit time. Average rate of the Cv reaction can be calculated: Time, t [Cv+] Average rate + Cresol violet (Cv ; a dye) decomposes in NaOH(aq): (s) (mol / L) (mol L-1 s-1) 0.0 5.000 x 10-5 13.2 x 10-7 10.0 3.680 x 10-5 9.70 x 10-7 20.0 2.710 x 10-5 7.20 x 10-7 30.0 1.990 x 10-5 5.30 x 10-7 40.0 1.460 x 10-5 3.82 x 10-7 + - 50.0 1.078 x 10-5 Cv (aq) + OH (aq) → CvOH(aq) 2.85 x 10-7 60.0 0.793 x 10-5 -7 + + -5 1.82 x 10 change in concentration of Cv Δ [Cv ] 80.0 0.429 x 10 rate = = 0.99 x 10-7 elapsed time Δt 100.0 0.232 x 10-5 © 2008 Brooks/Cole 5 © 2008 Brooks/Cole 6 1 Reaction Rates and Stoichiometry Reaction Rates and Stoichiometry Cv+(aq) + OH-(aq) → CvOH(aq) For any general reaction: a A + b B c C + d D Stoichiometry: The overall rate of reaction is: Loss of 1 Cv+ → Gain of 1 CvOH Rate of Cv+ loss = Rate of CvOH gain 1 Δ[A] 1 Δ[B] 1 Δ[C] 1 Δ[D] Rate = − = − = + = + Another example: a Δt b Δt c Δt d Δt 2 N2O5(g) 4 NO2(g) + O2(g) Reactants decrease with time.
    [Show full text]
  • Ochem ACS Review 23 Aryl Halides
    ACS Review Aryl Halides 1. Which one of the following has the weakest carbon-chlorine bond? A. I B. II C. III D. IV 2. Which compound in each of the following pairs is the most reactive to the conditions indicated? A. I and III B. I and IV C. II and III D. II and IV 3. Which of the following reacts at the fastest rate with potassium methoxide (KOCH 3) in methanol? A. fluorobenzene B. 4-nitrofluorobenzene C. 2,4-dinitrofluorobenzene D. 2,4,6-trinitrofluorobenzene 4. Which of the following reacts at the fastest rate with potassium methoxide (KOCH 3) in methanol? A. fluorobenzene B. p-nitrofluorobenzene C. p-fluorotoluene D. p-bromofluorobenzene 5. Which of the following is the kinetic rate equation for the addition-elimination mechanism of nucleophilic aromatic substitution? A. rate = k[aryl halide] B. rate = k[nucleophile] C. rate = k[aryl halide][nucleophile] D. rate = k[aryl halide][nucleophile] 2 6. Which of the following is not a resonance form of the intermediate in the nucleophilic addition of hydroxide ion to para -fluoronitrobenzene? A. I B. II C. III D. IV 7. Which chlorine is most susceptible to nucleophilic substitution with NaOCH 3 in methanol? A. #1 B. #2 C. #1 and #2 are equally susceptible D. no substitution is possible 8. What is the product of the following reaction? A. N,N-dimethylaniline B. para -chloro-N,N-dimethylaniline C. phenyllithium (C 6H5Li) D. meta -chloro-N,N-dimethylaniline 9. Which one of the reagents readily reacts with bromobenzene without heating? A.
    [Show full text]
  • Enzymatic Kinetic Isotope Effects from First-Principles Path Sampling
    Article pubs.acs.org/JCTC Enzymatic Kinetic Isotope Effects from First-Principles Path Sampling Calculations Matthew J. Varga and Steven D. Schwartz* Department of Chemistry and Biochemistry, University of Arizona, Tucson, Arizona 85721, United States *S Supporting Information ABSTRACT: In this study, we develop and test a method to determine the rate of particle transfer and kinetic isotope effects in enzymatic reactions, specifically yeast alcohol dehydrogenase (YADH), from first-principles. Transition path sampling (TPS) and normal mode centroid dynamics (CMD) are used to simulate these enzymatic reactions without knowledge of their reaction coordinates and with the inclusion of quantum effects, such as zero-point energy and tunneling, on the transferring particle. Though previous studies have used TPS to calculate reaction rate constants in various model and real systems, it has not been applied to a system as large as YADH. The calculated primary H/D kinetic isotope effect agrees with previously reported experimental results, within experimental error. The kinetic isotope effects calculated with this method correspond to the kinetic isotope effect of the transfer event itself. The results reported here show that the kinetic isotope effects calculated from first-principles, purely for barrier passage, can be used to predict experimental kinetic isotope effects in enzymatic systems. ■ INTRODUCTION staging method from the Chandler group.10 Another method that uses an energy gap formalism like QCP is a hybrid Particle transfer plays a crucial role in a breadth of enzymatic ff reactions, including hydride, hydrogen atom, electron, and quantum-classical approach of Hammes-Schi er and co-work- 1 ers, which models the transferring particle nucleus as a proton-coupled electron transfer reactions.
    [Show full text]
  • S.T.E.T.Women's College, Mannargudi Semester Iii Ii M
    S.T.E.T.WOMEN’S COLLEGE, MANNARGUDI SEMESTER III II M.Sc., CHEMISTRY ORGANIC CHEMISTRY - II – P16CH31 UNIT I Aliphatic nucleophilic substitution – mechanisms – SN1, SN2, SNi – ion-pair in SN1 mechanisms – neighbouring group participation, non-classical carbocations – substitutions at allylic and vinylic carbons. Reactivity – effect of structure, nucleophile, leaving group and stereochemical factors – correlation of structure with reactivity – solvent effects – rearrangements involving carbocations – Wagner-Meerwein and dienone-phenol rearrangements. Aromatic nucleophilic substitutions – SN1, SNAr, Benzyne mechanism – reactivity orientation – Ullmann, Sandmeyer and Chichibabin reaction – rearrangements involving nucleophilic substitution – Stevens – Sommelet Hauser and von-Richter rearrangements. NUCLEOPHILIC SUBSTITUTION Mechanism of Aliphatic Nucleophilic Substitution. Aliphatic nucleophilic substitution clearly involves the donation of a lone pair from the nucleophile to the tetrahedral, electrophilic carbon bonded to a halogen. For that reason, it attracts to nucleophile In organic chemistry and inorganic chemistry, nucleophilic substitution is a fundamental class of reactions in which a leaving group(nucleophile) is replaced by an electron rich compound(nucleophile). The whole molecular entity of which the electrophile and the leaving group are part is usually called the substrate. The nucleophile essentially attempts to replace the leaving group as the primary substituent in the reaction itself, as a part of another molecule. The most general form of the reaction may be given as the following: Nuc: + R-LG → R-Nuc + LG: The electron pair (:) from the nucleophile(Nuc) attacks the substrate (R-LG) forming a new 1 bond, while the leaving group (LG) departs with an electron pair. The principal product in this case is R-Nuc. The nucleophile may be electrically neutral or negatively charged, whereas the substrate is typically neutral or positively charged.
    [Show full text]
  • Alkyl Halides
    Alkyl Halides Alkyl halides are a class of compounds where a halogen atom or atoms are bound to an sp3 orbital of an alkyl group. CHCl3 (Chloroform: organic solvent) CF2Cl2 (Freon-12: refrigerant CFC) CF3CHClBr (Halothane: anesthetic) Halogen atoms are more electronegative than carbon atoms, and so the C-Hal bond is polarized. The C-Hal (often written C-X) bond is polarized in such a way that there is partial positive charge on the carbon and partial negative charge on the halogen. Ch06 Alkyl Halides (landscape).docx Page 1 Dipole moment Electronegativities decrease in the order of: F > Cl > Br > I Carbon-halogen bond lengths increase in the order of: C-F < C-Cl < C-Br < C-I Bond Dipole Moments decrease in the order of: C-Cl > C-F > C-Br > C-I = 1.56D 1.51D 1.48D 1.29D Typically the chemistry of alkyl halides is dominated by this effect, and usually results in the C-X bond being broken (either in a substitution or elimination process). This reactivity makes alkyl halides useful chemical reagents. Ch06 Alkyl Halides (landscape).docx Page 2 Nomenclature According to IUPAC, alkyl halides are treated as alkanes with a halogen (Halo-) substituent. The halogen prefixes are Fluoro-, Chloro-, Bromo- and Iodo-. Examples: Often compounds of CH2X2 type are called methylene halides. (CH2Cl2 is methylene chloride). CHX3 type compounds are called haloforms. (CHI3 is iodoform). CX4 type compounds are called carbon tetrahalides. (CF4 is carbon tetrafluoride). Alkyl halides can be primary (1°), secondary (2°) or tertiary (3°). Other types: A geminal (gem) dihalide has two halogens on the same carbon.
    [Show full text]
  • Microtest III Print File
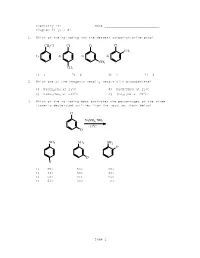
    Chemistry 211 Name ____________________________ Chapter 23 Quiz #1 1. Which of the following has the weakest carbon-chlorine bond? CH2Cl Cl Cl Cl CH3 1) 2) 3) 4) CH3 CH3 1) 1 2) 2 3) 3 4) 4 2. Which one of the reagents readily reacts with bromobenzene? 1) NaOCH2CH3 at 250C 2) NaCN/DMSO at 250C 3) NaNH2/NH3 at -330C 4) (CH3)2NH at 250C 3. Which of the following best estimates the percentages of the three isomeric deuterated anilines from the reaction shown below? Cl NaNH2, NH3 -33oC D NH 2 NH 2 NH 2 D D D 1) 25% 50% 25% 2) 33% 33% 33% 3) 50% 25% 25% 4) 66% 33% 0% Page 1 4. Which of the following is (are) true concerning the intermediate in the addition-elimination mechanism of the reaction below? F OCH3 NaOCH 3 intermediate NO2 NO2 A. The intermediate is aromatic. B. The intermediate is a resonance stabilized anion. C. Electron withdrawing groups on the benzene ring stabilize the intermediate. 1) only A 2) only B 3) A and C 4) B and C 5. Carbon-14 labelled chlorobenzene is reacted with sodium amide in ammonia as shown below. Which of the following depicts the carbon-14 label in the product(s)? Cl NaNH2/NH3 -33oC Cl Cl Cl 1) 3) and (about 50% of each) Cl Cl Cl 2) 4) and (about 50% of each) 1) 1 2) 2 3) 3 4) 4 6. Which of the following reacts at the fastest rate with potassium methoxide (KOCH3) in methanol? 1) fluorobenzene 2) 4-nitrofluorobenzene 3) 2,4-dinitrofluorobenzene 4) 2,4,6-trinitrofluorobenzene Page 2 7.
    [Show full text]
  • S 1 Reaction Remember That a 3˚ Alkyl Halide Will Not Undergo a S 2 Reaction the Steric Hindrance in the Transition State
    SN1 Reaction Remember that a 3˚ alkyl halide will not undergo a SN2 reaction The steric hindrance in the transition state is too high If t-Butyl iodide is reacted with methanol, however, a substitution product is obtained This product does NOT proceed through a SN2 reaction First proof is that the rate for the reaction does not depend on methanol concentration Occurs through a SN1 reaction Substitution – Nucleophilic – Unimolecular (1) SN1 - In a SN1 reaction the leaving group departs BEFORE a nucleophile attacks For t-butyl iodide this generates a planar 3˚ carbocation The carbocation can then react with solvent (or nucleophile) to generate the product If solvent reacts (like the methanol as shown) the reaction is called a “solvolysis” The Energy Diagram for a SN1 Reaction therefore has an Intermediate - And is a two step reaction CH3 Potential H3C energy CH3 I OCH CH3 3 H3C CH3 CH3 H3C CH3 Reaction Coordinate Why does a SN1 Mechanism Occur? - Whenever the potential energy of a reaction is disfavored for a SN2 reaction the SN1 mechanism becomes a possibility SN2 SN1 Potential energy I OCH3 CH3 H3C CH3 CH3 H3C CH3 Reaction Coordinate Rate Characteristics The rate for a SN1 reaction is a first order reaction Rate = k [substrate] The first step is the rate determining step The nucleophile is NOT involved in the rate determining step Therefore the rate of a SN1 reaction is independent of nucleophile concentration (or nucleophile characteristics, e.g. strength) What is Important for a SN1 Reaction? The primary factor concerning the rate of
    [Show full text]
  • Enthalpy and Free Energy of Reaction
    KINETICS AND THERMODYNAMICS OF REACTIONS Key words: Enthalpy, entropy, Gibbs free energy, heat of reaction, energy of activation, rate of reaction, rate law, energy profiles, order and molecularity, catalysts INTRODUCTION This module offers a very preliminary detail of basic thermodynamics. Emphasis is given on the commonly used terms such as free energy of a reaction, rate of a reaction, multi-step reactions, intermediates, transition states etc., FIRST LAW OF THERMODYNAMICS. o Law of conservation of energy. States that, • Energy can be neither created nor destroyed. • Total energy of the universe remains constant. • Energy can be converted from one form to another form. eg. Combustion of octane (petrol). 2 C8H18(l) + 25 O2(g) CO2(g) + 18 H2O(g) Conversion of potential energy into thermal energy. → 16 + 10.86 KJ/mol . ESSENTIAL FACTORS FOR REACTION. For a reaction to progress. • The equilibrium must favor the products- • Thermodynamics(energy difference between reactant and product) should be favorable • Reaction rate must be fast enough to notice product formation in a reasonable period. • Kinetics( rate of reaction) ESSENTIAL TERMS OF THERMODYNAMICS. Thermodynamics. Predicts whether the reaction is thermally favorable. The energy difference between the final products and reactants are taken as the guiding principle. The equilibrium will be in favor of products when the product energy is lower. Molecule with lowered energy posses enhanced stability. Essential terms o Free energy change (∆G) – Overall free energy difference between the reactant and the product o Enthalpy (∆H) – Heat content of a system under a given pressure. o Entropy (∆S) – The energy of disorderness, not available for work in a thermodynamic process of a system.
    [Show full text]
  • Kinetics and Mechanistic Investigation of Epoxide/CO2 Cycloaddition by a Synergistic Catalytic Effect of Pyrrolidinopyridinium Iodide and Zinc Halides
    Kinetics and mechanistic investigation of epoxide/CO2 cycloaddition by a synergistic catalytic effect of pyrrolidinopyridinium iodide and zinc halides Abdul Rehman a, b,*, Valentine C. Eze a, M.F.M. Gunam Resula, Adam Harveya a School of Engineering, Merz Court, Newcastle University, Newcastle Upon Tyne, NE1 7RU, UK b Department of Chemical and Polymer Engineering, University of Engineering and Technology Lahore, Faisalabad Campus, Pakistan *[email protected] Abstract Formation of styrene carbonate (SC) by the cycloaddition of CO2 to styrene oxide (SO) catalysed by pyrrolidinopyridinium iodide (PPI) in combination with zinc halides (ZnCl2, ZnBr2 and ZnI2) was investigated. Complete conversion of the SO to SC was achieved in 3 h with 100% selectivity using 1:0.5 molar (PPI/ZnI2) catalyst ratio under mild reaction conditions i.e. 100 °C and 10 bar CO2 pressure. The synergistic effect of ZnI2 and PPI resulted in more than 7-fold increase in reaction rate than using PPI alone. The cycloaddition reaction demonstrated the first-order dependence with respect to the epoxide, CO2 and catalyst concentrations. Moreover, the kinetic and thermodynamic activation parameters of SC formation were determined using the Arrhenius and Eyring equations. The positive values of ΔH‡ (42.8 kJ mol–1) and ΔG‡ (102.3 kJ mol–1) revealed endergonic and chemically controlled nature of the reaction, whereas the large negative values of ΔS‡ (–159.4 J mol–1 K–1) indicate a highly ordered activated complex at the transition state. The activation energy for SC formation catalyzed by PPI alone was found to be 73.2 kJ mol–1 over a temperature range of 100–140 °C, –1 which was reduced to 46.1 kJ mol when using PPI in combination with ZnI2 as a binary catalyst.
    [Show full text]
  • Chemical Kinetics, but Were Afraid to Ask…
    Everything You Always Wanted to Know (or better yet, need to know) About Chemical Kinetics, But Were Afraid to Ask… Overall Reactions An overall chemical reaction indicates reactants and products in the appropriate stoichiometric quantities. Overall chemical reactions can be used to predict quantities consumed or produced and write equilibrium expressions. Consequently, overall reactions are used in thermodynamic calculations, such as energy changes and equilibrium concentrations. However, the overall reaction provides no information about the molecular process involved in transforming reactants into products, the nature and number of individual steps involved, the presence of intermediates or the role of catalysis. Consequently, overall reactions provide no information about how fast a reaction proceeds or the various factors that influence reaction rates. For example, the overall reaction for the combustion of methane is given by; CH4(g) + O2(g) ==== CO2(g) + 2 H2O(g) From which we can write and equilibrium expression, calculate free energy changes and so on, but which provide little insight into how long it may take for the reaction to occur or what species might act as catalysts. Reaction Mechanisms Mechanisms provide the individual steps that occur on the molecular level in transforming reactants into products. (Whereas the overall reaction indicates where we start and end up, the mechanism tells us how we got there). Reaction mechanisms are composed of a series of elementary processes (steps) which are indicative of the molecular encounters. Because of this, mechanisms are intimately related to chemical kinetics. For example, the first two steps in the combustion of methane are given by; CH4 + OH Æ CH3 + H2O slow CH3 + O2 Æ CH3O2 fast Interestingly, mechanisms are never proven but rather postulated and checked for consistency with observed experimental kinetic data.
    [Show full text]
  • PDF (Chapter 5
    ~---=---5 __ Heterogeneous Catalysis 5.1 I Introduction Catalysis is a term coined by Baron J. J. Berzelius in 1835 to describe the property of substances that facilitate chemical reactions without being consumed in them. A broad definition of catalysis also allows for materials that slow the rate of a reac­ tion. Whereas catalysts can greatly affect the rate of a reaction, the equilibrium com­ position of reactants and products is still determined solely by thermodynamics. Heterogeneous catalysts are distinguished from homogeneous catalysts by the dif­ ferent phases present during reaction. Homogeneous catalysts are present in the same phase as reactants and products, usually liquid, while heterogeneous catalysts are present in a different phase, usually solid. The main advantage of using a hetero­ geneous catalyst is the relative ease of catalyst separation from the product stream that aids in the creation of continuous chemical processes. Additionally, heteroge­ neous catalysts are typically more tolerant ofextreme operating conditions than their homogeneous analogues. A heterogeneous catalytic reaction involves adsorption of reactants from a fluid phase onto a solid surface, surface reaction of adsorbed species, and desorption of products into the fluid phase. Clearly, the presence of a catalyst provides an alter­ native sequence of elementary steps to accomplish the desired chemical reaction from that in its absence. If the energy barriers of the catalytic path are much lower than the barrier(s) of the noncatalytic path, significant enhancements in the reaction rate can be realized by use of a catalyst. This concept has already been introduced in the previous chapter with regard to the CI catalyzed decomposition of ozone (Figure 4.1.2) and enzyme-catalyzed conversion of substrate (Figure 4.2.4).
    [Show full text]
  • Chemical Kinetics Study of the TIME Vs RATE of Chemical Change CHEMICAL KINETICS DEALS WITH
    Chemical Kinetics Study of the TIME vs RATE of Chemical Change CHEMICAL KINETICS DEALS WITH 1. How FAST {Speed like miles per hour} and 2. By what MECHANISM does a reaction happen? Part I How Fast (RATE) Does a Chemical Reaction “Go” ? What does the speed (RATE) depend upon? REACTION RATES • The change in the concentration of a reactant or product with time (M/s) for A → B ∆[A] ∆[B] Rate = − Rate = ∆t ∆t Rate disappearance = Rate of formation AFFECTS THE RATE 2A → B A disappears at twice the rate B forms Rate = - ½ ∆[A] = ∆[B] Rate disappearance ≠ Rate of formation For 2 N2O5 4 NO 2 + O 2 -7 If rate of decomposition of N 2O5 = 4.2 x 10 M/s What is the rate of APPEARANCE of (a) NO 2 ? Twice rate of decomposition = ________ M/s (b) O 2 ? ½ the rate of decomposition = _________ M/s How is the rate of the disappearance of the reactants related to the appearance of the products for CH 4(g) + 2O 2(g) →→→ CO 2(g) + 2H 2O( g) 1 ∆[CH ] 1 ∆[O ] 1 ∆[CO ] 1 ∆[H ] rate = − 4 = − 2 = 2 = 2 1 ∆t 2 ∆t 1 ∆t 2 ∆t Consider the reaction 3A --> 2B The average rate of appearance of B is given by [B]/ t. How is the average rate of appearance of B related to the average rate of disappear- ance of A? (a) -2[A]/3 t (b) 2[A]/3 t (c) -3[A]/2 t (d) [A]/ t (e) -[A]/ t Answer on Text Book’s Web Site 1.
    [Show full text]