DOCSLIB.ORG

What Does It Take to Accelerate SPICE on the GPU? | GTC 2013

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
What Does It Take to Accelerate SPICE on the GPU? | GTC 2013 What Does It Take to Accelerate SPICE on the GPU? M. Naumov, F. Lannutti, S. Chetlur, L.S. Chien and P. Vandermersch What is SPICE? . Simulation Program with Integrated Circuit Emphasis — First version was developed by Laurence Nagel in 1973 — http://en.wikipedia.org/wiki/SPICE . There exist many variations (not limited to) — Academic: ngspice, spice3 (UC – Berkeley), XSPICE (GeorgiaTech) — Industrial: HSPICE (Synopsys), Pspice (Cadence), Eldo (Mentor), EEsof (Agilent) What does SPICE do? Circuit (diagram): R R 1 1 2 3 3 R2 R4 Ixs Vs What does SPICE do? Circuit (diagram): Netlist (text file): nodes i j R R 1 1 2 3 3 R1 1 2 1k R2 2 0 1k R2 R4 Ixs Vs R3 2 3 0.4k R4 3 0 0.1k V1 1 0 PWL (0 0 1n 0 1.1n 5 2n 5) What does SPICE do? Circuit (diagram): Netlist (text file): nodes i j R R 1 1 2 3 3 R1 1 2 1k R2 2 0 1k R2 R4 Ixs Vs R3 2 3 0.4k R4 3 0 0.1k V1 1 0 PWL (0 0 1n 0 1.1n 5 2n 5) Physics (Kirchhoff + Ohms + ...): Resistor Stamp Voltage Source Stamp Sparse Matrix RHS Sparse Matrix RHS col col V V I V V I row i j xs row i j xs i 1/R -1/R i 1 j -1/R 1/R j -1 xs xs 1 -1 Vs What does SPICE do? Circuit (diagram): Netlist (text file): nodes i j R R 1 1 2 3 3 R1 1 2 1k R2 2 0 1k R2 R4 Ixs Vs R3 2 3 0.4k R4 3 0 0.1k V1 1 0 PWL (0 0 1n 0 1.1n 5 2n 5) Linear system (sparse): Physics (Kirchhoff + Ohms + ...): Resistor Stamp Voltage Source Stamp node 1 -1/R -1 Sparse Matrix RHS Sparse Matrix RHS 1/R1 1 V1 col col V V I node 2 (1/R +1/R +1/R ) Vi Vj Ixs i j xs -1/R1 1 2 3 -1/R3 V2 row row node 3 i 1/R -1/R i 1 -1/R3 (1/R3+1/R4) V3 source j -1/R 1/R j -1 1 Ixs Vs xs xs 1 -1 Vs SPICE Details . Input — Parse netlist and setup internal data structures . DC Analysis — Device model evaluation Newton-Raphson — Linear system solution . Transient Analysis — Device model evaluation For each time step: — Linear system solution - Newton-Raphson — Truncation error + Time step correction SPICE Details . Device Model Evaluation — Takes between 30%-60% of the simulation . DC Analysis — Device model evaluation Newton-Raphson — Linear system solution . Transient Analysis — Device model evaluation For each time step: — Linear system solution - Newton-Raphson — Truncation error + Time step correction SPICE Details . Linear System Solution — Takes between 30%-60% of the simulation . DC Analysis — Device model evaluation Newton-Raphson — Linear system solution . Transient Analysis — Device model evaluation For each time step: — Linear system solution - Newton-Raphson — Truncation error + Time step correction Device Model Evaluation . Basic models — Resistor, Capacitor, Inductor, Voltage and Current Source . Transistor models — MOSFET transistor (BSIM4v7, PSP, etc.) — Bipolar transistor (Ebers–Moll, Gummel-Poon, etc.) . Other models — Diodes, etc. Device Model Evaluation . Basic models — Resistor, Capacitor, Inductor, Voltage and Current Source . Transistor models focus of this presentation — MOSFET transistor (BSIM4v7, PSP, etc.) — Bipolar transistor (Ebers–Moll, Gummel-Poon, etc.) . Other models — Diodes, etc. Device Model Evaluation . Key Idea (Transistor - BSIM4v7) if() if() — Many branches are related to fixed parameters if() ... Temperature else ... Operation Regime else ... — Reorganize the code (slightly) . Minimize thread divergence . Maximize memory coalescing T1 T2 T3 T4 ... T10K ... T100K ... Tn BSIM4v7 ... Instances Basic Device Model Evaluation 40 35 Resistor Netlist Capacitor Netlist 30 Inductor Netlist 25 20 Speedup 15 10 5 0 8192 16384 32768 65536 131072 1) Resistor Netlist: all resistors; number of instances of models* 2) Capacitor Netlist: half capacitors and half resistors; 3) Inductor Netlist: half resistors, quarter capacitors and quarter inductors; *NGSPICE Performance may vary based on *NVIDIA C2070, ECC on OS version and motherboard configuration *Intel X5690 (Nehalem, 6 CoreTM) @ 3.47GHz Transistor (BSIM4v7) Device Model Evaluation 60 CPU (1 core) 6.67x 50 GPU 40 30 Time (ms) Time 20 10 0 ISCAS85 Benchmark Suite *NGSPICE Performance may vary based on *NVIDIA C2070, ECC on OS version and motherboard configuration *Intel X5690 (Nehalem, 6 CoreTM) @ 3.47GHz Solution of Linear Systems . Solve a set of (sparse) linear systems Ai xi = fi for i=1,...,k where the coefficient matrices Ai have the same sparsity pattern . Matrix properties — Nonsymmetric — Ill-conditioned . Different methods — Direct Methods (LU factorization + triangular solve) — Iterative Methods (GMRES, BiCGStab, etc.) Solution of Linear Systems . Solve a set of (sparse) linear systems Ai xi = fi for i=1,...,k where the coefficient matrices Ai have the same sparsity pattern . Matrix properties — Nonsymmetric — Ill-conditioned focus of this presentation . Different methods — Direct Methods (LU factorization + triangular solve) — Iterative Methods (GMRES, BiCGStab, etc.) Sparse Direct Methods . Original linear system A x = f . Reordering (to minimize fill-in) (A Q) (QT x) = f where QTQ=QQT=I . Pivoting (PT A Q) (QT x) = PT f where PTP=PPT=I . LU factorization (PT A Q) = L U . Forward and backward (triangular) solve L (U y) = b where y = QT x and b = PT x Sparse Direct Methods . Recall — Solving a set of linear systems — Coefficient matrices have the same sparsity pattern . Assume — reordering (to minimize fill-in) is the same — pivoting is also constant . LU factorization (i=1) focus of this presentation (PT A Q) = L U . LU re-factorization (i=2,...,k) — Sparsity (the required memory) of L and U is known ahead of time GLU: LU re-factorization on the GPU . Key Idea — LU-factorization A = LU — Incomplete-LU factorization (zeroed) (zeroed) M = L +U +A equivalent GLU: LU re-factorization on the GPU . Key Idea Solving a set of systems Ai xi = fi (i=1,...,k) — LU-factorization A = L U (i=1) A = LU 1 1 1 — Incomplete-LU factorization (zeroed) (zeroed) M = L (zeroed)+U (zeroed)+A M = L +U +A i 1 1 i (i=2,...,k) equivalent GLU: LU re-factorization on the GPU . Key Idea Solving a set of systems Ai xi = fi (i=1,...,k) — LU-factorization A = L U (i=1) A = LU 1 1 1 — Incomplete-LU factorization (zeroed) (zeroed) M = L (zeroed)+U (zeroed)+A M = L +U +A i 1 1 i (i=2,...,k) equivalent — Many parallel techniques are applicable GLU: LU re-factorization on the GPU . GLU — Developed in CUDA programming language for GPUs — Sparsity pattern of L and U known ahead of time — Memory requirements known ahead of time . vs. KLU, which is — Designed specifically for circuit simulation — Gilbert-Peierls (single threaded) . vs. PARDISO, which is — Supernodal method (multi-threaded) Test matrices can be found at Review of sparse direct solvers can be found at http://www.cise.ufl.edu/research/sparse/matrices/ http://www.cise.ufl.edu/research/sparse/codes/ GLU Speedup (C2070) 14.3 7.5 7.0|25.2 4 GLU vs. KLU (1t) GLU vs. PARDISO (6t) 3 2 Speedup 1 0 rajat17 rajat23 trans4 G2_circuit transient ASIC_680ks ASIC_680k G3_circuit Freescale1 circuit5M Performance may vary based on *NVIDIA C2070, ECC on OS version and motherboard configuration *Intel X5680 (Nehalem, 6 CoreTM) @ 3.33GHz, MKL 10.3.6 GLU Speedup (K20x) 16.1 8.6 7.0|5.4 4 GLU vs. KLU (1t) GLU vs. PARDISO (8t) 3 2 Speedup 1 0 rajat17 rajat23 trans4 G2_circuit transient ASIC_680ks ASIC_680k G3_circuit Freescale1 circuit5M Performance may vary based on * NVIDIA K20, ECC on OS version and motherboard configuration * Intel E5-2687w (Sandy Bridge, 8 CoreTM) @ 3.1GHz, MKL 10.3.6 GLU Speedup (K20x) 16.1 8.6 7.0|5.4 4 GLU vs. KLU (1t) GLU vs. PARDISO (8t) 3 2 Speedup 1 0 rajat17 rajat23 trans4 G2_circuit transient ASIC_680ks ASIC_680k G3_circuit Freescale1 circuit5M Average Speedup vs. KLU: 2x Performance may vary based on * NVIDIA K20, ECC on OS version and motherboard configuration * Intel E5-2687w (Sandy Bridge, 8 CoreTM) @ 3.1GHz, MKL 10.3.6 GLU Speedup (K20x) 16.1 8.6 7.0|5.4 4 GLU vs. KLU (1t) GLU vs. PARDISO (8t) 3 2 Speedup 1 0 rajat17 rajat23 trans4 G2_circuit transient ASIC_680ks ASIC_680k G3_circuit Freescale1 circuit5M Average Speedup vs. PARDISO: 2.5x Performance may vary based on * NVIDIA K20, ECC on OS version and motherboard configuration * Intel E5-2687w (Sandy Bridge, 8 CoreTM) @ 3.1GHz, MKL 10.3.6 Conclusion . SPICE simulation two most time consuming parts — Device model evaluation — Solution of linear systems . Device model evaluation — Speedup* of up to 6x . Solution of linear systems — Speedup* (average) of 2x . GPU (overall) acceleration — SPICE (overall expected) speedup of 2-3x — No slowdown: easy to test an iteration (and revert back if needed) *: speedup is dependent on input parameters Thank you Questions? .
Load more

Recommended publications
  • Circuit Design and Analysis Temel Elektrik Mühendisli Ği, Cilt 1 , Fitzgerald
    Course Plan Ankara University Credit: 4 ECTS Engineering Faculty Class: Lecture: 3 hours Department of Engineering Physics Problem Hours: 0 Lab: 0 PEN207 Class Hours: Monday 09:30-12:15 (3 hours) CIRCUIT DESIGN AND Classroom: Seminar Hall (Seminer Salonu) ANALYSIS Office Hours: Friday 11:00-12:00 (Circuit Theory) Attendance: Mandatory Exams: Midterm (one midterm exam) % 30 Prof. Dr. Hüseyin Sarı Final Exam % 80 Passing Grade: 60 (C3) or higher 3 Course Materials and Textbook(s) Ankara University Engineering Faculty, Lecture notes (Ppoint): Dept. of Engineering Physics huseyinsari.net.tr Desler Circuit Design & Analysis (http://huseyinsari.net.tr/ders-pen207.htm) 2019 Fall Main book: PEN207 Circuit Design and Analysis Temel Elektrik Mühendisli ği, Cilt 1 , Fitzgerald. A. E. Higginbotham D. E.,Grabel A. Instructor : Prof. Dr. Hüseyin Sarı (Editor: Prof. Dr. Kerim Kıymaç, 3.Edition) A.U. Engineering Faculty, Dept. of Eng. Physics Office: Department of Eng. Phy., B-Block, Room:105 E-mail: [email protected] ● [email protected] web: www.huseyinsari.net.tr Phone: (312) 203 3424 (office) ● 536 295 3555 (cell) 2 4 PEN207-Circuit Design & Analysis:Introduction 1 Textbooks Textbooks-Turkish Recommended Textbooks-1: Recommended (Turkish)Textbooks-3: Introductory Electric Circuits Schaum's Outline of Basic Circuit Elektrik Devreleri Elektrik Devreleri Elektrik Devreleri-I Circuit Analysis James W. Nilsson, James W. Nilsson, (Ders Kitabı ) - Teori ve Çözümlü Robert L. Boylestad Susan Riedel Analysis, 2nd Edition John O'Malley Susan Riedel Problem Çözümleri Örnekler Pearson Int. Edition 6th Ed. Palme Yayınevi (In library) (In library) (In library) Turgut İkiz , Ali Bekir Yıldız Papatya Bilim Yayınları Volga Yayıncılık 5 7 Textbooks Textbooks-Turkish Recommended Textbooks-2: Recommended (Turkish)Textbooks-4: Introduction to Electrical Schaum's Outline of Do ğru Akım Devreleri ve Electric Circuits Engineering: 3000 Solved Problem Çözümleri Richard C.
    [Show full text]
  • SPICE 1: Tutorial
    SPICE 1: Tutorial Chris Winstead January 15, 2015 Chris Winstead SPICE 1: Tutorial January 15, 2015 1 / 28 Getting Started SPICE is designed to run as a classic console tool, aka a terminal command. If you are unfamiliar with the Linux terminal, you should spend some time to get acquainted with basic terminal commands, and how to organize and navigate directory structures (a directory is often called a \folder"). I prepared a quick-start terminal tutorial that you can review here: https://electronics.wiki.usu.edu/Linux_Tutorial If you plan to use NGSpice in the lab (which I recommend), then you may want to check out our NGSpice wiki page: https://electronics.wiki.usu.edu/NGSpice You can also find NGSpice information and the full manual here: http://ngspice.sourceforge.net/ You will also need to choose a text editor for preparing your SPICE files. I like to use Emacs (it has an optional SPICE mode that is pretty handy). Most students prefer to use GEdit. You can launch these editors from the terminal. Chris Winstead SPICE 1: Tutorial January 15, 2015 2 / 28 Creating a Project First, you'll want to open a terminal window and create a directory tree for your work this semester. You could setup your directory tree using these commands: cd mkdir 3410 cd 3410 mkdir spice cd spice mkdir lab1 cd lab1 Here the cd command is used to change directories, and the mkdir command is used to create a directory. Chris Winstead SPICE 1: Tutorial January 15, 2015 3 / 28 Create a new SPICE file SPICE files (often called \decks" for historical reasons) are plain text files.
    [Show full text]
  • NGSPICE: Circuit Simulator User Guide for ECE 391
    NGSPICE: Circuit Simulator User guide for ECE 391 Last Updated: August 2015 Preface This user guide contains several page references to the ngspice re-work manual version 26. The official ngspice manual can be found at http://ngspice.sourceforge.net/ as well as older ver- sions available for download. Oregon State University i Acknowledgments Oregon State University ii Contents Preface i Acknowledgments ii 1 Introduction 1 2 How to Install Ngspice 1 2.1 Mac OS X . .1 2.2 Linux Distros . .2 2.3 Windows . .3 2.4 Alternative Method - remotely (PuTTY) . .3 3 How to Run Ngspice 3 3.1 Using PuTTY . .3 3.2 Using Windows . .4 4 Ngspice Overview 5 4.1 Getting Started . .5 4.2 Creating a Netlist . .6 4.3 Creating Circuit Elements . .7 5 Transmissions Lines 10 5.1 Transmission Line (lossless) . 10 5.1.1 Voltage Sources . 10 5.1.2 Creating a Transmission Line . 11 5.2 Transmission Lines (lossy) . 14 6 Subcircuits 16 6.1 Creating a Subcircuit . 17 7 AC - Standing Waves 21 7.1 Standing Wave Examples . 21 7.2 Standing Wave plots . 22 Ngspice User Guide - ECE 391 1 Introduction This ngspice user guide has been developed for the ECE 391 course at Oregon State University to assist students to further their understanding on the behavior of transmission lines. This guide covers the basic concepts to using ngspice to simulate ideal (lossless) and non-ideal (lossy) trans- mission lines in DC/AC circuits and other related topics discussed in the course. This user guide summarizes the useful, pertinent information from the near 600 page ngspice manual needed to run the ngspice simulator for this course, while adding several extra examples.
    [Show full text]
  • Circuit Optimisation Using Device Layout Motifs
    Circuit Optimisation using Device Layout Motifs Yang Xiao Ph.D. University of York Electronics July 2015 Abstract Circuit designers face great challenges as CMOS devices continue to scale to nano dimensions, in particular, stochastic variability caused by the physical properties of transistors. Stochas- tic variability is an undesired and uncertain component caused by fundamental phenomena associated with device structure evolution, which cannot be avoided during the manufac- turing process. In order to examine the problem of variability at atomic levels, the `Motif ' concept, defined as a set of repeating patterns of fundamental geometrical forms used as design units, is proposed to capture the presence of statistical variability and improve the device/circuit layout regularity. A set of 3D motifs with stochastic variability are investigated and performed by technology computer aided design simulations. The statistical motifs compact model is used to bridge between device technology and circuit design. The statistical variability information is transferred into motifs' compact model in order to facilitate variation-aware circuit designs. The uniform motif compact model extraction is performed by a novel two-step evolutionary algorithm. The proposed extraction method overcomes the drawbacks of conventional extraction methods of poor convergence without good initial conditions and the difficulty of simulating multi-objective optimisations. After uniform motif compact models are obtained, the statistical variability information is injected into these compact models to generate the final motif statistical variability model. The thesis also considers the influence of different choices of motif for each device on cir- cuit performance and its statistical variability characteristics. A set of basic logic gates is constructed using different motif choices.
    [Show full text]
  • Scientific Tools for Linux
    Scientific Tools for Linux Ryan Curtin LUG@GT Ryan Curtin Getting your system to boot with initrd and initramfs - p. 1/41 Goals » Goals This presentation is intended to introduce you to the vast array Mathematical Tools of software available for scientific applications that run on Electrical Engineering Tools Linux. Software is available for electrical engineering, Chemistry Tools mathematics, chemistry, physics, biology, and other fields. Physics Tools Other Tools Questions? Ryan Curtin Getting your system to boot with initrd and initramfs - p. 2/41 Non-Free Mathematical Tools » Goals MATLAB (MathWorks) Mathematical Tools » Non-Free Mathematical Tools » MATLAB » Mathematica Mathematica (Wolfram Research) » Maple » Free Mathematical Tools » GNU Octave » mathomatic Maple (Maplesoft) »R » SAGE Electrical Engineering Tools S-Plus (Mathsoft) Chemistry Tools Physics Tools Other Tools Questions? Ryan Curtin Getting your system to boot with initrd and initramfs - p. 3/41 MATLAB » Goals MATLAB is a fully functional mathematics language Mathematical Tools » Non-Free Mathematical Tools You may be familiar with it from use in classes » MATLAB » Mathematica » Maple » Free Mathematical Tools » GNU Octave » mathomatic »R » SAGE Electrical Engineering Tools Chemistry Tools Physics Tools Other Tools Questions? Ryan Curtin Getting your system to boot with initrd and initramfs - p. 4/41 Mathematica » Goals Worksheet-based mathematics suite Mathematical Tools » Non-Free Mathematical Tools Linux versions can be buggy and bugfixes can be slow » MATLAB
    [Show full text]
  • Ngspice User's Manual (Version 32)
    Ngspice User’s Manual Version 32 (Describes ngspice release version) Holger Vogt, Marcel Hendrix, Paolo Nenzi May 2nd, 2020 2 Locations The project and download pages of ngspice may be found at Ngspice home page http://ngspice.sourceforge.net/ Project page at SourceForge http://sourceforge.net/projects/ngspice/ Download page at SourceForge http://sourceforge.net/projects/ngspice/files/ Git source download http://sourceforge.net/scm/?type=cvs&group_id=38962 Status This manual is a work in progress. Some to-dos are listed in Chapt. 24.3. More is surely needed. You are invited to report bugs, missing items, wrongly described items, bad English style, etc. How to use this Manual The manual is a “work in progress.” It may accompany a specific ngspice release, e.g. ngspice- 24 as manual version 24. If its name contains ‘Version xxplus’, it describes the actual code status, found at the date of issue in the Git Source Code Management (SCM) tool. This manual is intended to provide a complete description of ngspice’s functionality, features, commands, and procedures. This manual is not a book about learning SPICE usage, however the novice user may find some hints how to start using ngspice. Chapter 21.1 gives a short introduction how to set up and simulate a small circuit. Chapter 32 is about compiling and installing ngspice from a tarball or the actual Git source code, which you may find on the ngspice web pages. If you are running a specific Linux distribution, you may check if it provides ngspice as part of the package.
    [Show full text]
  • Ngspice User Manual
    Ngspice User’s Manual Version 35 plus (ngspice development version) Holger Vogt, Marcel Hendrix, Paolo Nenzi, Dietmar Warning September 27, 2021 2 Locations The project and download pages of ngspice may be found at Ngspice home page http://ngspice.sourceforge.net/ Project page at SourceForge http://sourceforge.net/projects/ngspice/ Download page at SourceForge https://sourceforge.net/projects/ngspice/files/ng-spice- rework/ Git source download https://sourceforge.net/p/ngspice/ngspice/ci/master/tree/ Status This manual is a work in progress. Some to-dos are listed in Chapt. 24.3. More is surely needed. You are invited to report bugs, missing items, wrongly described items, bad English style, etc. How to use this Manual The manual is a “work in progress.” It may accompany a specific ngspice release, e.g. ngspice-35 as manual version 35. If its name contains ‘Version xxplus’, it describes the actual code status, found at the date of issue in the Git Source Code Management (SCM) tool. This manual is intended to provide a complete description of ngspice’s functionality, features, commands, and procedures. This manual is not a book about learning SPICE usage, however the novice user may find some hints how to start using ngspice. Chapter 21.1 gives a short introduction how to set up and simulate a small circuit. Chapter 32 is about compiling and installing ngspice from a tarball or the actual Git source code, which you may find on the ngspice web pages. If you are running a specific Linux distribution, you may check if it provides ngspice as part of the package.
    [Show full text]
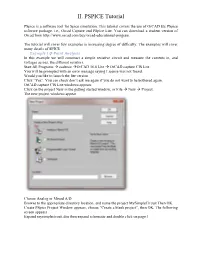
  • II. PSPICE Tutorial
    II. PSPICE Tutorial PSpice is a software tool for Spice simulation. This tutorial covers the use of OrCAD EE PSpice software package, i.e., Orcad Capture and PSpice Lite. You can download a student version of Orcad from http://www.orcad.com/buy/orcad-educational-program. The tutorial will cover few examples in increasing degree of difficulty. The examples will cover many details of SPICE. Example I Q-Point Analysis In this example we will construct a simple resistive circuit and measure the currents in, and voltages across, the different resistors. Start All Programs à cadence àOrCAD 16.6 Lite à OrCAD capture CIS Lite You will be prompted with an error message saying License was not found. Would you like to launch the lite version Click “Yes”. You can check don’t ask me again if you do not want to be bothered again. OrCAD capture CIS Lite windows appears Click on the project New in the getting started window, or File à New à Project. The new project windows appear Choose Analog or Mixed A/D Browse to the appropriate directory location, and name the project MySimpleCircuit Then OK. Create PSpice Project Window appears, choose “Create a blank project”, then OK. The following screen appears Expand mysimplecircuit.dsn then expand schematic and double click on page 1 Place part Place wire Select Place part Place wire Place net alias Place ground You will get the schematic page, with a ground node in it and text to tell you to copy and paste the ground in your design. Every circuit must contain a ground and the name of the node is “0” that is the number zero.
    [Show full text]
  • Hardware Description Language Modelling and Synthesis of Superconducting Digital Circuits
    Hardware Description Language Modelling and Synthesis of Superconducting Digital Circuits Nicasio Maguu Muchuka Dissertation presented for the Degree of Doctor of Philosophy in the Faculty of Engineering, at Stellenbosch University Supervisor: Prof. Coenrad J. Fourie March 2017 Stellenbosch University https://scholar.sun.ac.za Declaration By submitting this dissertation electronically, I declare that the entirety of the work contained therein is my own, original work, that I am the sole author thereof (save to the extent explicitly otherwise stated), that reproduction and publication thereof by Stellenbosch University will not infringe any third party rights and that I have not previously in its entirety or in part submitted it for obtaining any qualification. Signature: N. M. Muchuka Date: March 2017 Copyright © 2017 Stellenbosch University All rights reserved i Stellenbosch University https://scholar.sun.ac.za Acknowledgements I would like to thank all the people who gave me assistance of any kind during the period of my study. ii Stellenbosch University https://scholar.sun.ac.za Abstract The energy demands and computational speed in high performance computers threatens the smooth transition from petascale to exascale systems. Miniaturization has been the art used in CMOS (complementary metal oxide semiconductor) for decades, to handle these energy and speed issues, however the technology is facing physical constraints. Superconducting circuit technology is a suitable candidate for beyond CMOS technologies, but faces challenges on its design tools and design automation. In this study, methods to model single flux quantum (SFQ) based circuit using hardware description languages (HDL) are implemented and thereafter a synthesis method for Rapid SFQ circuits is carried out.
    [Show full text]
  • XSCHEM PDF Manual
    XSCHEM 0.29 Manual and Tutorials XSCHEM : schematic capture and netlisting EDA tool Xschem is a schematic capture program, it allows creation of hierarchical representation of circuits with a top down approach . By focusing on interfaces, hierarchy and instance properties a complex system can be described in terms of simpler building blocks. A VHDL or Verilog or Spice netlist can be generated from the drawn schematic, allowing the simulation of the circuit. Key feature of the program is its drawing engine written in C and using directly the Xlib drawing primitives; this gives very good speed performance, even on very big circuits. The user interface is built with the Tcl-Tk toolkit, tcl is also the extension language used. Features hierarchical schematic drawings, no limits on size any object in the schematic can have any sort of properties (generics in VHDL, parameters in Spice or Verilog) new Spice/Verilog primitives can be created, and the netlist format can be defined by the user tcl extension language allows the creation of scripts; any user command in the drawing window has an associated tcl comand VHDL / Verilog / Spice netlist, ready for simulation Behavioral VHDL / Verilog code can be embedded as one of the properties of the schematic block, Xschem runs on UNIX systems with X11 and Tcl-Tk toolkit installed. Documentation XSCHEM manual Download Current release Old XSCHEM releases on Sourceforge SVN: svn checkout svn://repo.hu/xschem/trunk License 1 XSCHEM 0.29 Manual and Tutorials The software is released under the GNU GPL,
    [Show full text]
  • Download Easyeda PDF Tutorial
    EasyEDA Tutorial 2020.06.14 v6.3.53 EasyEDA Editor：https://lceda.cn/editor EasyEDA Desktop Client：https://lceda.cn/download Remark This document will be updated as the new features of the editor are updated. The latest revison please refer at EasyEDA Tutorials.pdf Editor FAQ Please spend a few minutes reading this FAQ, it will save you lots of time getting started with EasyEDA. Video Tutorials https://www.youtube.com/channel/UCRoMhHNzl7tMW8pFsdJGUIA/videos Contact Us https://docs.easyeda.com/en/FAQ/Contact-Us/index.html Update Records Update Records Can I use EasyEDA in my company? You are free to use EasyEDA for individuals, business and education. If you add our Logo and link on your PCB/Video we will appreciate. I don't like others seeing my design. How can I stop that happening? Set your project as Private. For extra security you can even save your work locally. What happens if EasyEDA service is offline for some reason? EasyEDA can be run as an offline application. Is EasyEDA safe? There are no absolutely secure things in the world but even if you have the misfortune - as happened to one of our team - of losing one laptop and having two hard drives break, EasyEDA will try to protect your designs in following ways: 1. We utilize SSL throughout the entire domain EasyEDA.com. Secure Socket Layer (SSL) technology encrypts all data transferred between your computer and our servers. Your data is for your eyes only. 2. You can save your files locally. 3. Multiple copies of every file are saved in your local database.
    [Show full text]
  • Scheme & Syllabus M.Tech. Course
    SCHEME & SYLLABUS for M.TECH. COURSE in VLSI DESIGN (w.e.f. Session 2018-2019) DEPARTMENT OF ELECTRONICS ENGINEERING YMCA UNIVERSITY OF SCIENCE AND TECHNOLOGY FARIDABAD VISION YMCA University of Science and Technology aspires to be a nationally and internationally acclaimed leader in technical and higher education in all spheres which transforms the life of students through integration of teaching, research and character building. MISSION • To contribute to the development of science and technology by synthesizing teaching, research and creative activities. • To provide an enviable research environment and state-of-the-art technological exposure to its scholars. • To develop human potential to its fullest extent and make them emerge as world class leaders in their professions and enthuse them towards their social responsibilities. Department of Electronics Engineering VISION To be a Centre of Excellence for producing high quality engineers and scientists capable of providing sustainable solutions to complex problems and promoting cost effective indigenous technology in the area of Electronics, Communication & Control Engineering for Industry, Research Organizations, Academia and all sections of society. MISSION • To frame a well-balanced curriculum with an emphasis on basic theoretical knowledge as well the requirements of the industry. • To motivate students to develop innovative solutions to the existing problems for betterment of the society. • Collaboration with the industry, research establishments and other academic institutions to bolster the research and development activities. • To provide infrastructure and financial support for culmination of novel ideas into useful prototypes. • To promote research in emerging and interdisciplinary areas and act as a facilitator for knowledge generation and dissemination through Research, Institute - Industry and Institute- Institute interaction.
    [Show full text]