DOCSLIB.ORG

Digital Control Networks for Virtual Creatures

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Digital Control Networks for Virtual Creatures Digital control networks for virtual creatures Christopher James Bainbridge Doctor of Philosophy School of Informatics University of Edinburgh 2010 Abstract Robot control systems evolved with genetic algorithms traditionally take the form of floating-point neural network models. This thesis proposes that digital control sys- tems, such as quantised neural networks and logical networks, may also be used for the task of robot control. The inspiration for this is the observation that the dynamics of discrete networks may contain cyclic attractors which generate rhythmic behaviour, and that rhythmic behaviour underlies the central pattern generators which drive low- level motor activity in the biological world. To investigate this a series of experiments were carried out in a simulated physically realistic 3D world. The performance of evolved controllers was evaluated on two well known control tasks — pole balancing, and locomotion of evolved morphologies. The performance of evolved digital controllers was compared to evolved floating-point neu- ral networks. The results show that the digital implementations are competitive with floating-point designs on both of the benchmark problems. In addition, the first re- ported evolution from scratch of a biped walker is presented, demonstrating that when all parameters are left open to evolutionary optimisation complex behaviour can result from simple components. iii Acknowledgements “I know why you’re here... I know what you’ve been doing... why you hardly sleep, why you live alone, and why night after night, you sit by your computer.” I would like to thank my parents and grandmother for all of their support over the years, and for giving me the freedom to pursue my interests from an early age. My time at Edinburgh would not have been so enjoyable without my friends and flatmates; in particular I must thank J.D. for his friendship and kindred humour, Big C. for the nights of Teviot and snakebite, Ljiljana for her remarkable ability to share a room with me for three years and not go insane, Javier, Sasha and Jude for the similar skills of flat sharing, Nicki, Evie and Marian for being there, and everyone in the university ju-jitsu club for providing years of social interactions, the complexity of which, when graphed, might put a neural network to shame. From my life before Edinburgh: Frank, John, Ian and Brian for the crazy nights in Consett, including the impromptu ju-jitsu demonstration that almost got us arrested. And from a time long past: the inhabitants of the DnC BBS who gave me the inspiration and motivation to sit every night playing with code, networks, and Unix. And to my younger brother, Paul, who as he points out, has had a job for a long time now... Without various pieces of software this project would not have been possible. I would like to thank the authors of the following open source systems which I use every day: Linux, the Open Dynamics Engine (ODE) and PyODE, Screen, KDE and KPDF/Okular, R, Python, teTeX, Vim, ZODB/ZEO, Git, Firefox, and MPlayer. This thesis was greatly improved thanks to valuable feedback from Gillian Hayes and Susan Stepney. iv Declaration I declare that this thesis was composed by myself, that the work contained herein is my own except where explicitly stated otherwise in the text, and that this work has not been submitted for any other degree or professional qualification except as specified. (Christopher James Bainbridge) v Table of Contents 1 Introduction 1 1.1 Motivation . 1 1.2 Contributions to knowledge . 7 1.3 Reproducibility . 11 1.4 Summary . 12 1.5 Organisation of the thesis . 14 2 Biological sensing and control 17 2.1 Neural networks . 17 2.2 Biological models . 22 2.3 Connectivity and resilience . 22 2.4 Pattern generation for muscle control . 28 2.5 Sensory feedback . 31 2.6 Brain computer interfaces . 32 2.7 Summary . 35 3 Synthetic neural networks 39 3.1 Similarities to biological networks . 42 3.2 Connectivity . 43 3.3 State and signal coding . 44 3.3.1 Example codings . 46 3.4 Models of single neuron dynamics . 49 3.4.1 Input function . 49 3.4.2 Activation function . 50 3.4.3 Output function . 50 3.4.4 Spiking models . 52 3.4.5 Continuous models . 57 vii 3.4.6 Reduced models . 61 3.5 Computational power . 75 3.6 Robot control . 76 3.7 Training . 76 3.7.1 Backpropagation . 77 3.8 Hardware acceleration . 79 3.9 Summary . 82 4 Other networks 83 4.1 Analog circuits . 84 4.2 Digital circuits . 85 4.3 Asynchronous circuits . 86 4.4 Genetic regulatory networks . 89 4.5 Boolean networks . 94 4.5.1 Random boolean networks . 96 4.6 Generalised logical networks . 102 4.7 Cellular automata . 106 4.8 The edge of chaos . 110 4.9 Summary . 111 5 Genetic evolution 115 5.1 Natural selection . 116 5.2 Genetics in nature . 117 5.3 Genetic algorithms . 124 5.4 Modularity of the genome . 126 5.5 Fitness function . 127 5.6 Fitness surface . 128 5.7 Search behaviour . 131 5.8 Genotype encoding . 132 5.8.1 Example encodings . 134 5.9 Population models . 135 5.10 Initial population creation . 136 5.11 Parent selection . 136 5.12 Reproduction . 138 5.13 Summary . 140 viii 6 Evolution of specific genotypes 143 6.1 Problem specific operators . 144 6.2 Evolving flocking . 146 6.3 Ant colonies . 148 6.4 Evolving neural networks for robot control . 150 6.4.1 Timeline . 152 6.5 Evolving reduced continuous neural models . 157 6.6 Evolving reduced spiking neural models . 158 6.7 Evolving modular hierarchical neural networks . 158 6.8 Evolving genetic regulatory networks . 161 6.9 Evolving cellular automata . 161 6.9.1 Evolving cellular automata neural networks . 164 6.10 Evolving analog circuits . 168 6.10.1 Evolving FPAA robot control . 168 6.10.2 Evolving FPGA oscillators . 169 6.10.3 Evolving FPGA frequency discriminators . 169 6.10.4 Evolving on an analog FPTA . 170 6.10.5 Evolving fault tolerance . 171 6.11 Evolving digital circuits . 172 6.11.1 Optimising gate count . 173 6.11.2 Optimising power . 174 6.11.3 Evolving digital circuits for robot control . 176 6.12 Evolving pattern generators . 176 6.12.1 Timeline . 177 6.13 Evolving morphology . 180 6.13.1 Timeline . 181 6.14 Evolving robot morphology and control . 193 6.14.1 Timeline . 194 6.15 Evolving modular robots . 211 6.16 Summary . 212 7 Overview so far 217 8 Software design 219 8.1 Creature morphology . 219 8.2 Morphogenesis . 221 ix 8.3 Evolution of the morphology . 223 8.4 Example morphologies . 224 8.5 Neurogenesis . 225 8.6 Neural network topologies . 233 8.7 Neuron quantisation . 236 8.8 Evolution of the neural networks . 237 8.9 The software . 238 8.10 Simulated physics . 244 8.10.1 Collision detection . 245 8.11 Sensors and actuators . 246 8.12 Motor models . 246 8.12.1 Stimulus-response curves of PD motor controller . 247 8.13 Physics simulation problems . 250 8.14 Tasks . 256 8.15 Summary . 256 9 Software testing 257 9.1 Testing neuron models . 259 9.1.1 Explanation of graphs . 260 9.1.2 Sine model . 262 9.1.3 Sigmoid model . ..
Load more

Recommended publications
  • Master's Thesis
    MASTER'S THESIS Online Model Predictive Control of a Robotic System by Combining Simulation and Optimization Mohammad Rokonuzzaman Pappu 2015 Master of Science (120 credits) Space Engineering - Space Master Luleå University of Technology Department of Computer Science, Electrical and Space Engineering Mohammad Rokonuzzaman Pappu Online Model Predictive Control of a Robotic System by Combining Simulation and Optimization School of Electrical Engineering Department of Electrical Engineering and Automation Thesis submitted in partial fulfillment of the requirements for the degree of Master of Science in Technology Espoo, August 18, 2015 Instructor: Professor Perttu Hämäläinen Aalto University School of Arts, Design and Architecture Supervisors: Professor Ville Kyrki Professor Reza Emami Aalto University Luleå University of Technology School of Electrical Engineering Preface First of all, I would like to express my sincere gratitude to my supervisor Pro- fessor Ville Kyrki for his generous and patient support during the work of this thesis. He was always available for questions and it would not have been possi- ble to finish the work in time without his excellent guidance. I would also like to thank my instructor Perttu H¨am¨al¨ainen for his support which was invaluable for this thesis. My sincere thanks to all the members of Intelligent Robotics group who were nothing but helpful throughout this work. Finally, a special thanks to my colleagues of SpaceMaster program in Helsinki for their constant support and encouragement. Espoo, August 18,
    [Show full text]
  • Rhythms of the Brain
    Rhythms of the Brain György Buzsáki OXFORD UNIVERSITY PRESS Rhythms of the Brain This page intentionally left blank Rhythms of the Brain György Buzsáki 1 2006 3 Oxford University Press, Inc., publishes works that further Oxford University’s objective of excellence in research, scholarship, and education. Oxford New York Auckland Cape Town Dar es Salaam Hong Kong Karachi Kuala Lumpur Madrid Melbourne Mexico City Nairobi New Delhi Shanghai Taipei Toronto With offices in Argentina Austria Brazil Chile Czech Republic France Greece Guatemala Hungary Italy Japan Poland Portugal Singapore South Korea Switzerland Thailand Turkey Ukraine Vietnam Copyright © 2006 by Oxford University Press, Inc. Published by Oxford University Press, Inc. 198 Madison Avenue, New York, New York 10016 www.oup.com Oxford is a registered trademark of Oxford University Press All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior permission of Oxford University Press. Library of Congress Cataloging-in-Publication Data Buzsáki, G. Rhythms of the brain / György Buzsáki. p. cm. Includes bibliographical references and index. ISBN-13 978-0-19-530106-9 ISBN 0-19-530106-4 1. Brain—Physiology. 2. Oscillations. 3. Biological rhythms. [DNLM: 1. Brain—physiology. 2. Cortical Synchronization. 3. Periodicity. WL 300 B992r 2006] I. Title. QP376.B88 2006 612.8'2—dc22 2006003082 987654321 Printed in the United States of America on acid-free paper To my loved ones. This page intentionally left blank Prelude If the brain were simple enough for us to understand it, we would be too sim- ple to understand it.
    [Show full text]
  • Team-Fly® Power up Your Mind
    Power Up Your Mind:Y L Learn faster,F work smarterM A E T Bill Lucas NICHOLAS BREALEY PUBLISHING Team-Fly® Power Up Your Mind Learn faster, work smarter Bill Lucas N ICHOLAS B REALEY P UBLISHING LONDON First published by Nicholas Brealey Publishing in 2001 Reprinted (twice) 2002 3–5 Spafield Street PO Box 700 Clerkenwell, London Yarmouth EC1R 4QB, UK Maine 04096, USA Tel: +44 (0)20 7239 0360 Tel: (888) BREALEY Fax: +44 (0)20 7239 0370 Fax: (207) 846 5181 http://www.nbrealey-books.com http://www.powerupyourmind.com © Bill Lucas 2001 The right of Bill Lucas to be identified as the author of this work has been asserted in accordance with the Copyright, Designs and Patents Act 1988. ISBN 1-85788-275-X British Library Cataloguing in Publication Data A catalogue record for this book is available from the British Library. Library of Congress Cataloging-in-Publication Data Lucas, Bill. Power up your mind : learn faster, work smarter / Bill Lucas. p. cm. Includes bibliographical references and index. ISBN 1-85788-275-X 1. Learning, Psychology of. 2. Work--Psychological aspects. I. Title. BF318 .L83 2001 153.1′5--dc21 2001035940 All rights reserved. No part of this publication may be reproduced, stored in a retrieval system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording and/or otherwise without the prior written permission of the publishers. This book may not be lent, resold, hired out or otherwise disposed of by way of trade in any form, binding or cover other than that in which it is published, without the prior consent of the publishers.
    [Show full text]
  • Control Theory
    Control theory S. Simrock DESY, Hamburg, Germany Abstract In engineering and mathematics, control theory deals with the behaviour of dynamical systems. The desired output of a system is called the reference. When one or more output variables of a system need to follow a certain ref- erence over time, a controller manipulates the inputs to a system to obtain the desired effect on the output of the system. Rapid advances in digital system technology have radically altered the control design options. It has become routinely practicable to design very complicated digital controllers and to carry out the extensive calculations required for their design. These advances in im- plementation and design capability can be obtained at low cost because of the widespread availability of inexpensive and powerful digital processing plat- forms and high-speed analog IO devices. 1 Introduction The emphasis of this tutorial on control theory is on the design of digital controls to achieve good dy- namic response and small errors while using signals that are sampled in time and quantized in amplitude. Both transform (classical control) and state-space (modern control) methods are described and applied to illustrative examples. The transform methods emphasized are the root-locus method of Evans and fre- quency response. The state-space methods developed are the technique of pole assignment augmented by an estimator (observer) and optimal quadratic-loss control. The optimal control problems use the steady-state constant gain solution. Other topics covered are system identification and non-linear control. System identification is a general term to describe mathematical tools and algorithms that build dynamical models from measured data.
    [Show full text]
  • War in the Age of Intelligent Machines
    Introduction The image of the ''killer robot" once belonged uniquely to the world of science fiction. This is still so, of course, but only if one thinks of human­ like mechanical contraptions scheming to conquer the planet. The latest weapons systems planned by the Pentagon, however, offer a less anthropo­ morphic example of what machines with "predatory capabilities" might be like: pilotless aircraft and unmanned tanks "intelligent" enough to be able to select and destroy their own targets. Although the existing prototypes of robotic weapons, like the PROWLER or the BRAVE 3000, are not yet truly autonomous, these new weapons do demonstrate that even if Artificial Intel­ ligence is not at present sufficiently sophisticated to create true "killer robots,'' when synthetic intelligence does make its appearance on the planet, there will already be a predatory role awaiting it. The PROWLER, for example, is a small terrestrial armed vehicle, equipped with a primitive form of "machine vision" (the capability to ana­ lyze the contents of a video frame) that allows it to maneuver around a battlefield and distinguish friends from enemies. Or at least this is the aim of the robot's designers. In reality, the PROWLER still has difficulty negoti­ ating sharp turns or maneuvering over rough terrain, and it also has poor friend/foe recognition capabilities. For these reasons it has been deployed only for very simple tasks, such as patrolling a military installation along a predefined path. We do not know whether the PROWLER has ever opened fire on an intruder without human supervision, but it is doubtful that as currently designed this robot has been authorized to kill humans on its own.
    [Show full text]
  • The Platinum Rule® F O R S a L E S M Ast E R Y
    The Platinum Rule® FO R SALE S M ast E R Y Dr. Tony Alessandra Scott Michael Zimmerman and Dr. Joseph La Lopa PLATINUM RULE GROUP, LLC. The Platinum Rule® FO R S A L E S M ast E R Y © Copyright 2009 • All rights reserved in all media. Dr. Tony Alessandra, Scott Michael Zimmerman and Dr. Joseph La Lopa No part of this publication may be reproduced or transmitted in any form or by any means, mechanical or electronic, including photocopying and recording, or by any information storage and retrieval system, without permission in writing from author or publisher (except by a reviewer, who may quote brief passages and/or show brief video clips in review). ISBN: 0-000000-00-0 (Hardcover) ISBN: 978-0-9819371-2-0 (Paperback) ISBN: 0-000000-00-0 (Audio) ISBN: 0-000000-00-0 (eBook) Published by: Cover & Interior Design by: Glenn Griffiths www.TheCyranoGroup.com Platinum Rule Group, LLC. 600 31st Street SW Barberton, Ohio 44203 1-330-848-0444 www.PlatinumRule.com ACKNOWLEDGE M EN ts WE ARE GRATEFUL TO ALL OF THE PSYCHOLOGISTS, sociologists, visionaries, philosophers, coaches, consultants, trainers, speakers and authors who directly and indirectly influenced our work, documented their findings and who built foundations of evidence upon which we could build. Just a sampling of these include: Michael J. O’Connor, Katherine Briggs, Jim Cathcart, Roger Dawson, John Geier, Paul Green, Phil Hunsaker, Carl Jung, Florence Littauer, Russ Watson, William Moulton Marston, David McClelland, David Merrill, Roger Reid, Larry Wilson, Bill Schwarz, Isabel Briggs Myers, Don Lowry, Janice Van Dyke and Don Hutson.
    [Show full text]
  • What Is Persona?
    What is Monsters and Other Childish Things? Monsters and Other Childish Things (MaOCT) is a roleplaying game written by Benjamin Baugh, based on Wild Talents by Dennis Detwiller and Greg Stolze, using the One Roll Engine (O.R.E.) that Stolze designed. In it, the players control school-age Kids (Elementary through High School, usually) who are accompanied by horrible, slavering, nightmarish Monsters that also happen to be a Kid’s best friend. They have adventures, deal with school bullies (hopefully with words, not by eating them), experiences crushes (again, hopefully without eating them) and discover the horrible secrets of other worlds on the fringes of human awareness. Good fun is had by all. What is Persona? Persona is a Japanese Roleplaying Video Game series made by Atlus. A spin-off of the Shin Megami Tensei series, Persona focuses on high schoolers pitted jointly against other-worldly forces and the crushing gravity of their own social obligations and psychological trauma. Their instrument for dealing with these are Personas: manifestations of psycho-spiritual power that come to their aid and defense. In each of the Persona games, the player controls a group of Persona users who must unravel the mysteries of some supernatural phenomena that threatens the existence of their friends, town, or even the entire world. What am I reading? The Velvet Book is a conversion module for MaOCT designed to optimize its rules for running a game inspired by the Persona series. In truth, you can run Persona with MaOCT’s vanilla rules; the Drunk and Ugly Podcast did an entire series like that (check out “Shin Megami Tensei and Other Childish Things”) and it worked just fine.
    [Show full text]
  • Software Design for Pluggable Real Time Physics Middleware
    2005:270 CIV MASTER'S THESIS AgentPhysics Software Design for Pluggable Real Time Physics Middleware Johan Göransson Luleå University of Technology MSc Programmes in Engineering Department of Computer Science and Electrical Engineering Division of Computer Science 2005:270 CIV - ISSN: 1402-1617 - ISRN: LTU-EX--05/270--SE AgentPhysics Software Design for Pluggable Real Time Physics Middleware Johan GÄoransson Department of Computer Science and Electrical Engineering, LuleºaUniversity of Technology, [email protected] October 27, 2005 Abstract This master's thesis proposes a software design for a real time physics appli- cation programming interface with support for pluggable physics middleware. Pluggable means that the actual implementation of the simulation is indepen- dent and interchangeable, separated from the user interface of the API. This is done by dividing the API in three layers: wrapper, peer, and implementation. An evaluation of Open Dynamics Engine as a viable middleware for simulating rigid body physics is also given based on a number of test applications. The method used in this thesis consists of an iterative software design based on a literature study of rigid body physics, simulation and software design, as well as reviewing related work. The conclusion is that although the goals set for the design were ful¯lled, it is unlikely that AgentPhysics will be used other than as a higher level API on top of ODE, and only ODE. This is due to a number of reasons such as middleware speci¯c tools and code containers are di±cult to support, clash- ing programming paradigms produces an error prone implementation layer and middleware developers are reluctant to port their engines to Java.
    [Show full text]
  • Nonverbal Dictionary
    The The NONVERBAL DICTIONARY of GESTURES, SIGNS & BODY LANGUAGE CUES From Adam's-Apple-Jump to Zygomatic Smile By David B. Givens © 2002 (Spokane, Washington: Center for Nonverbal Studies Press) Items in this Dictionary have been researched by anthropologists, archaeologists, biologists, linguists, psychiatrists, psychologists, semioticians, and others who have studied human communication from a scientific point of view. Every effort has been made to cite their work in the text. Definitions, meanings, and interpretations left uncredited are those of the author. Gestures and consumer products with http://members.aol.com/nonverbal2/diction1.htm (1 of 2) [27/04/02 05:54:42] The current trademark registrations are identified with the ® symbol. Entries in The Dictionary. There have been many who, not knowing how to mingle the useful and the pleasing in the right proportions, have had all their toil and pains for nothing . --Cervantes (Don Quixote) Dedication "A masterful piece of work" --American Library Association "Highly recommended" --New Scientist "Very interesting reading" --The Houston Chronicle "Monumental" --Yahoo! Picks of the Week "Site of the Day Award" --WWW Virtual Library WWW Virtual Library "Best" Site © 2002 by David B. Givens, Ph.D. Center for Nonverbal Studies http://members.aol.com/nonverbal2/diction1.htm (2 of 2) [27/04/02 05:54:42] adajum ADAM'S-APPLE-JUMP Body movement. 1. A conspicuous up-and-down motion of the Adam's apple. 2. A movement of the throat visible while gulping or swallowing, as in nervousness. Usage: The Adam's-apple-jump is an unconscious sign of emotional anxiety, embarrassment, or stress.
    [Show full text]
  • Physics Engine Design and Implementation Physics Engine • a Component of the Game Engine
    Physics engine design and implementation Physics Engine • A component of the game engine. • Separates reusable features and specific game logic. • basically software components (physics, graphics, input, network, etc.) • Handles the simulation of the world • physical behavior, collisions, terrain changes, ragdoll and active characters, explosions, object breaking and destruction, liquids and soft bodies, ... Game Physics 2 Physics engine • Example SDKs: – Open Source • Bullet, Open Dynamics Engine (ODE), Tokamak, Newton Game Dynamics, PhysBam, Box2D – Closed source • Havok Physics • Nvidia PhysX PhysX (Mafia II) ODE (Call of Juarez) Havok (Diablo 3) Game Physics 3 Case study: Bullet • Bullet Physics Library is an open source game physics engine. • http://bulletphysics.org • open source under ZLib license. • Provides collision detection, soft body and rigid body solvers. • Used by many movie and game companies in AAA titles on PC, consoles and mobile devices. • A modular extendible C++ design. • Used for the practical assignment. • User manual and numerous demos (e.g. CCD Physics, Collision and SoftBody Demo). Game Physics 4 Features • Bullet Collision Detection can be used on its own as a separate SDK without Bullet Dynamics • Discrete and continuous collision detection. • Swept collision queries. • Generic convex support (using GJK), capsule, cylinder, cone, sphere, box and non-convex triangle meshes. • Support for dynamic deformation of nonconvex triangle meshes. • Multi-physics Library includes: • Rigid-body dynamics including constraint solvers. • Support for constraint limits and motors. • Soft-body support including cloth and rope. Game Physics 5 Design • The main components are organized as follows Soft Body Dynamics Bullet Multi Threaded Extras: Maya Plugin, Rigid Body Dynamics etc. Collision Detection Linear Math, Memory, Containers Game Physics 6 Overview • High level simulation manager: btDiscreteDynamicsWorld or btSoftRigidDynamicsWorld.
    [Show full text]
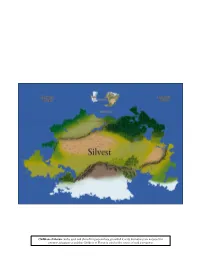
  • Children of Horun a Fantasy Setting with Guidelines for D&D 5E
    Children of Horun A fantasy setting with guidelines for D&D 5e Children of Horun can be used and shared for personal use, provided it or its derivatives are not used for commercial purposes and that Children of Horun is cited as the source of said derivatives. Introduction Horun is a vast world, inhabited by people of many creeds and cultures from a number of different intelligent species. It is a world where the past has been buried, time and time again, where reality can be manipulated though study and force of will. It is, in a phrase, a fantastic world. Children of Horun is a fantasy role-playing setting suited for many playstyles, with emphasis on political intrigue. It is a medium-magic, low-divine setting; magic is common but magic items are not, learning anything but the most cursory spells is quite difficult, and there are no true gods to derive power from or to influence the world. In terms of atmosphere, Horun varies widely. Campaigns with an emphasis on overcoming adversity or playing one's part in a greater societal structure will work well. On the other hand, standard “great adventurers rising to become demigods” campaigns may not fit the world's theme very well at all. What you use this document for is ultimately up to you. This document is a comprehensive guide of the people, animals, and places of Horun, meant for players and game masters alike. Feel free to share and use this document as you like for non-commercial use, so long as you give credit where credit is due! Chapter 1: The Children of Horun “And so, we split among ourselves, spreading across the world and establishing ourselves among the lifeforms that piqued our interests.
    [Show full text]
  • Dynamic Simulation of Manipulation & Assembly Actions
    Syddansk Universitet Dynamic Simulation of Manipulation & Assembly Actions Thulesen, Thomas Nicky Publication date: 2016 Document version Peer reviewed version Document license Unspecified Citation for pulished version (APA): Thulesen, T. N. (2016). Dynamic Simulation of Manipulation & Assembly Actions. Syddansk Universitet. Det Tekniske Fakultet. General rights Copyright and moral rights for the publications made accessible in the public portal are retained by the authors and/or other copyright owners and it is a condition of accessing publications that users recognise and abide by the legal requirements associated with these rights. • Users may download and print one copy of any publication from the public portal for the purpose of private study or research. • You may not further distribute the material or use it for any profit-making activity or commercial gain • You may freely distribute the URL identifying the publication in the public portal ? Take down policy If you believe that this document breaches copyright please contact us providing details, and we will remove access to the work immediately and investigate your claim. Download date: 09. Sep. 2018 Dynamic Simulation of Manipulation & Assembly Actions Thomas Nicky Thulesen The Maersk Mc-Kinney Moller Institute Faculty of Engineering University of Southern Denmark PhD Dissertation Odense, November 2015 c Copyright 2015 by Thomas Nicky Thulesen All rights reserved. The Maersk Mc-Kinney Moller Institute Faculty of Engineering University of Southern Denmark Campusvej 55 5230 Odense M, Denmark Phone +45 6550 3541 www.mmmi.sdu.dk Abstract To grasp and assemble objects is something that is known as a difficult task to do reliably in a robot system.
    [Show full text]