DOCSLIB.ORG

1 Regional Climate Model 2 Calculating Cloud Base Heights

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
1 Regional Climate Model 2 Calculating Cloud Base Heights Supplementary Material to accompany Climate Change Scenario for Costa Rican Montane Forests A. V. Karmalkar, R. S. Bradley, H. F. Diaz 1 Regional Climate Model The PRECIS (Providing REgional Climates for Impact Studies) model is derived from the third-generation Hadley Center regional climate model (HadRM3) and is based on HadAM3P, an improved version of the atmo- spheric component of the latest Hadley Center coupled AOGCM (HadCM3). It is an atmospheric and land surface model of limited area and high reso- lution and can be positioned over any part of the globe. Dynamical flow, clouds and precipitation, radiative processes, the land surface and the deep soil are all described. It is forced at the lateral boundaries by HadAM3P GCM. The lateral boundary conditions comprise the standard atmospheric variables of surface pressure, horizontal wind components and measures of atmospheric temperature and humidity. The surface boundary conditions include observed sea surface temperatures (SSTs) and sea-ice. There is no prescribed constraint at the upper boundary of the model. The model has 19 vertical levels, the lowest at ∼50m and the highest at 0.5 hPa with terrain-following σ-coordinates (σ = pressure/surface pressure) used for the bottom four levels, purely pressure coordinates for the top three levels and a combination in between. Due to its fine resolution, the model requires a timestep of 5 minutes to maintain numerical stability. We carried out sim- ulations over the region of Central America (Fig.S1) at a resolution of 25 km. The model results presented in this paper are based on one member of the ensemble. 2 Calculating Cloud Base Heights Along the windward slopes of Costa Rica, the moisture-laden air is orograph- ically uplifted as the trade winds encounter the cordillera. If we assume an air parcel that cools at a dry adiabatic lapse rate without an input or loss of moisture, then we can calculate the lifting condensation level (LCL), the level at which a raising air parcel becomes saturated. The LCL coincides with the cloud base level. The vapor pressure and the saturation vapor 1 pressure are calculated using the following equations. L 1 1 e = e0 × exp − (1) Rv T0 TD L 1 1 es = e0 × exp − (2) Rv T0 T where, T0 = 273.15K, e0 = 0.611kP a, T is surface air temperature, and TD is the dew point temperature. Relative humidity (RH) is given as, e RH = × 100 (3) es Since the model gives us T and RH at the surface, TD can be calculated. Equations (1),(2) and (3) result in the following formula for the dew point temperature as a function of T and RH. T ln(RH/100)−1 TD = T 1 − (4) L/Rv 6 −1 −1 −1 where, L = 2.453 × 10 JKg , and Rv = 461JK Kg . Now we can calculate the pressure at the LCL (mbar) using the following formula (Geogagakos and Bras, 1984), 1 P = P (5) LCL 3.5 surf T −TD 223.15 + 1 where, Psurf is the surface pressure. The pressure at LCL allows us to cal- culate the cloud base heights using model geopotential heights. The cloud bases are calculated for dry season months (Dec-Feb) using mean monthly T and RH values. This exercise is to determine what the altitude of cloud formation would be if the air from lower elevations is lifted adiabatically. This is one of the reasons why we chose grid-points with elevation less than 800 m for this analysis. Furthermore, the horizontal grid resolution of the model is larger in size than any individual cloud, and the model RH does not reach 100% for individual grid-points (Fig.S2). For this reason, the LCL estimates always lie above the grid-point elevation, which is not always true for higher elevations. Also the altitude of cloud formation cannot be deter- mined by looking at 100% RH surface. Therefore there is some difficulty in estimating the actual height of the cloud bank. Nevertheless, the relative humidity surface can be used as a grid-scale cloud cover proxy. Figure S2 2 shows the RH values as a function of elevation along a transect in Costa Rica for the control and SRES A2 runs. These show a reduction in RH at all elevations in future. Reference Georgakakos, K.P. and Bras, R.L. (1984). A hydrologically useful station precipitation model. 1.Formulation. Water Resources Research, 20 (11), 1585-1596. 3.
Load more

Recommended publications
  • 3.2 the Forecast Icing Potential (Fip) Algorithm
    3.2 THE FORECAST ICING POTENTIAL (FIP) ALGORITHM Frank McDonough *, Ben C. Bernstein, Marcia K. Politovich, and Cory A. Wolff National Center for Atmospheric Research, Boulder, CO 1. Introduction The 70% threshold was chosen to allow for expected model moisture errors and to allow for In-flight icing is a serious hazard to the cold clouds to be found without a model forecast aviation community. It occurs when subfreezing of water saturation. The use of a combination of liquid cloud and/or precipitation droplets freeze to relative humidity with respect to both water and ice the exposed surfaces of an aircraft in flight. Icing may allow for the use of a higher threshold in conditions can occur on large scales or in small future versions of FIP. volumes where conditions may change quickly. Cloud base is found by working upward in the Because of the nature of icing conditions, the need same column until the first level with RH≥80% is for a forecast product with high spatial and found. Since the model boundary layer often has temporal resolution is apparent. RH>80%, even in cloud-free air, FIP begins its The FIP (Forecast Icing Potential) algorithm search for a cloud base at 1000ft (305m) AGL. was developed at the National Center for The threshold of 80% for cloud base identification Atmospheric Research under the Federal Aviation is used to also allow for model moisture errors and Administration’s Aviation Weather Research the expectation that cloud base is found at warmer Program. It uses 20-km resolution Rapid Update temperatures where RH and RHi are more Cycle (RUC) model output to determine the equivalent.
    [Show full text]
  • VIIRS Cloud Base Height Algorithm Theoretical Basis Document (ATBD)
    Effective Date: April 22, 2011 Revision - GSFC JPSS CMO December 5, 2011 Released Joint Polar Satellite System (JPSS) Ground Project Code 474 474-00045 Joint Polar Satellite System (JPSS) VIIRS Cloud Base Height Algorithm Theoretical Basis Document (ATBD) For Public Release The information provided herein does not contain technical data as defined in the International Traffic in Arms Regulations (ITAR) 22 CFC 120.10. This document has been approved For Public Release to the NOAA Comprehensive Large Array-data Stewardship System (CLASS). Goddard Space Flight Center Greenbelt, Maryland National Aeronautics and Space Administration Check the JPSS MIS Server at https://jpssmis.gsfc.nasa.gov/frontmenu_dsp.cfm to verify that this is the correct version prior to use. JPSS VIIRS Cloud Base Height ATBD 474-00045 Effective Date: April 22, 2011 Revision - This page intentionally left blank. Check the JPSS MIS Server at https://jpssmis.gsfc.nasa.gov/frontmenu_dsp.cfm to verify that this is the correct version prior to use. JPSS VIIRS Cloud Base Height ATBD 474-00045 Effective Date: April 22, 2011 Revision - Joint Polar Satellite System (JPSS) VIIRS Cloud Base Height Algorithm Theoretical Basis Document (ATBD) JPSS Electronic Signature Page Prepared By: Neal Baker JPSS Data Products and Algorithms, Senior Engineering Advisor (Electronic Approvals available online at https://jpssmis.gsfc.nasa.gov/mainmenu_dsp.cfm ) Approved By: Heather Kilcoyne DPA Manager (Electronic Approvals available online at https://jpssmis.gsfc.nasa.gov/mainmenu_dsp.cfm ) Goddard Space Flight Center Greenbelt, Maryland i Check the JPSS MIS Server at https://jpssmis.gsfc.nasa.gov/frontmenu_dsp.cfm to verify that this is the correct version prior to use.
    [Show full text]
  • Glossary of Severe Weather Terms
    Glossary of Severe Weather Terms -A- Anvil The flat, spreading top of a cloud, often shaped like an anvil. Thunderstorm anvils may spread hundreds of miles downwind from the thunderstorm itself, and sometimes may spread upwind. Anvil Dome A large overshooting top or penetrating top. -B- Back-building Thunderstorm A thunderstorm in which new development takes place on the upwind side (usually the west or southwest side), such that the storm seems to remain stationary or propagate in a backward direction. Back-sheared Anvil [Slang], a thunderstorm anvil which spreads upwind, against the flow aloft. A back-sheared anvil often implies a very strong updraft and a high severe weather potential. Beaver ('s) Tail [Slang], a particular type of inflow band with a relatively broad, flat appearance suggestive of a beaver's tail. It is attached to a supercell's general updraft and is oriented roughly parallel to the pseudo-warm front, i.e., usually east to west or southeast to northwest. As with any inflow band, cloud elements move toward the updraft, i.e., toward the west or northwest. Its size and shape change as the strength of the inflow changes. Spotters should note the distinction between a beaver tail and a tail cloud. A "true" tail cloud typically is attached to the wall cloud and has a cloud base at about the same level as the wall cloud itself. A beaver tail, on the other hand, is not attached to the wall cloud and has a cloud base at about the same height as the updraft base (which by definition is higher than the wall cloud).
    [Show full text]
  • PHAK Chapter 12 Weather Theory
    Chapter 12 Weather Theory Introduction Weather is an important factor that influences aircraft performance and flying safety. It is the state of the atmosphere at a given time and place with respect to variables, such as temperature (heat or cold), moisture (wetness or dryness), wind velocity (calm or storm), visibility (clearness or cloudiness), and barometric pressure (high or low). The term “weather” can also apply to adverse or destructive atmospheric conditions, such as high winds. This chapter explains basic weather theory and offers pilots background knowledge of weather principles. It is designed to help them gain a good understanding of how weather affects daily flying activities. Understanding the theories behind weather helps a pilot make sound weather decisions based on the reports and forecasts obtained from a Flight Service Station (FSS) weather specialist and other aviation weather services. Be it a local flight or a long cross-country flight, decisions based on weather can dramatically affect the safety of the flight. 12-1 Atmosphere The atmosphere is a blanket of air made up of a mixture of 1% gases that surrounds the Earth and reaches almost 350 miles from the surface of the Earth. This mixture is in constant motion. If the atmosphere were visible, it might look like 2211%% an ocean with swirls and eddies, rising and falling air, and Oxygen waves that travel for great distances. Life on Earth is supported by the atmosphere, solar energy, 77 and the planet’s magnetic fields. The atmosphere absorbs 88%% energy from the sun, recycles water and other chemicals, and Nitrogen works with the electrical and magnetic forces to provide a moderate climate.
    [Show full text]
  • A Novel Technique for Extracting Clouds Base Height Using Ground Based Imaging
    Atmos. Meas. Tech., 4, 117–130, 2011 www.atmos-meas-tech.net/4/117/2011/ Atmospheric doi:10.5194/amt-4-117-2011 Measurement © Author(s) 2011. CC Attribution 3.0 License. Techniques A novel technique for extracting clouds base height using ground based imaging E. Hirsch1, E. Agassi2, and I. Koren1 1Weizmann Institute, Department of Environmental Sciences, Rehovot, 76100, Israel 2Israel Institute for Biological Research, Department of Environmental Physics, Nes-Ziona, Israel Received: 13 September 2010 – Published in Atmos. Meas. Tech. Discuss.: 4 October 2010 Revised: 3 January 2011 – Accepted: 22 January 2011 – Published: 28 January 2011 Abstract. The height of a cloud in the atmospheric column 1 Introduction is a key parameter in its characterization. Several remote sensing techniques (passive and active, either ground-based Parameterization of cloud fields in the atmosphere has cru- or on space-borne platforms) and in-situ measurements are cial importance for atmospheric science (Kiehl and Tren- routinely used in order to estimate top and base heights of berth, 1997) and aviation safety (Schafer et al., 2004) ap- clouds. In this article we present a novel method that com- plications. Remote cloud sensing techniques can be char- bines thermal imaging from the ground and sounded wind acterized by the observation point – space or ground based profile in order to derive the cloud base height. This method measurements, and by the sensing method – either active is independent of cloud types, making it efficient for both low (cloud/rain radar, LIDAR) or passive. In addition, cloud boundary layer and high clouds. In addition, using thermal boundaries can be retrieved by in-situ measurements of the imaging ensures extraction of clouds’ features during day- atmospheric profile with radiosonde.
    [Show full text]
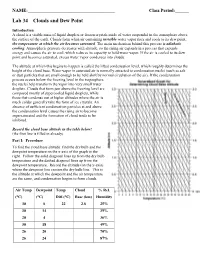
  • Lab 34 Clouds and Dew Point
    NAME:______________________________________ Class Period:______ Lab 34 Clouds and Dew Point Introduction A cloud is a visible mass of liquid droplets or frozen crystals made of water suspended in the atmosphere above the surface of the earth. Clouds form when air containing invisible water vapor rises and cools to its dew point, the temperature at which the air becomes saturated. The main mechanism behind this process is adiabatic cooling. Atmospheric pressure decreases with altitude, so the rising air expands in a process that expends energy and causes the air to cool, which reduces its capacity to hold water vapor. If the air is cooled to its dew point and becomes saturated, excess water vapor condenses into clouds. The altitude at which this begins to happen is called the lifted condensation level, which roughly determines the height of the cloud base. Water vapor in saturated air is normally attracted to condensation nuclei (such as salt or dust particles that are small enough to be held aloft by normal circulation of the air). If the condensation process occurs below the freezing level in the troposphere, the nuclei help transform the vapor into very small water droplets. Clouds that form just above the freezing level are composed mostly of supercooled liquid droplets, while those that condense out at higher altitudes where the air is much colder generally take the form of ice crystals. An absence of sufficient condensation particles at and above the condensation level causes the rising air to become supersaturated and the formation of cloud tends to be inhibited. Record the cloud base altitude in the table below! (the first line is filled in already) Part I: Procedure To find the cloud base altitude: find the dry bulb and the dewpoint temperature on the x-axis of the graph to the right.
    [Show full text]
  • Skew-T Diagram Dr
    ESCI 341 – Meteorology Lesson 18 – Use of the Skew-T Diagram Dr. DeCaria Reference: The Use of the Skew T, Log P Diagram in Analysis And Forecasting, AWS/TR-79/006, U.S. Air Force, revised 1979 (Air Force Skew-T Manual) An Introduction to Theoretical Meteorology, Hess SKEW-T/LOG P DIAGRAM Uses Rd ln p as the vertical coordinate Since pressure decreases exponentially with height, this coordinate means that the vertical coordinate roughly represents altitude. Uses T K ln p as the horizontal coordinate (K is an arbitrary constant). This means that isotherms, instead of being vertical, are slanted upward to the right with a slope of (K). With these coordinates, adiabats are lines that are semi-straight, and slope upward to the left. K is chosen so that the adiabat-isotherm angle is near 90. Areas on a skew-T/log p diagram are proportional to energy per unit mass. Pseudo-adiabats (moist-adiabats) are curved lines that are nearly vertical at the bottom of the chart, and bend so that they become nearly parallel to the adiabats at lower pressures. Mixing ratio lines (isohumes) slope upward to the right. USE OF THE SKEW-T/LOG P DIAGRAM The skew-T diagram can be used to determine many useful pieces of information about the atmosphere. The first step to using the diagram is to plot the temperature and dew point values from the sounding onto the diagram. Temperature (T) is usually plotted in black or blue, and dew point (Td) in green. Stability Stability is readily checked on the diagram by comparing the slope of the temperature curve to the slope of the moist and dry adiabats.
    [Show full text]
  • Cloud Top Properties and Cloud Phase Algorithm Theoretical Basis Document
    CLOUD TOP PROPERTIES AND CLOUD PHASE ALGORITHM THEORETICAL BASIS DOCUMENT W. Paul Menzel Space Science and Engineering Center University of Wisconsin – Madison Richard A. Frey Cooperative Institute for Meteorological Satellite Studies University of Wisconsin - Madison Bryan A. Baum Space Science and Engineering Center University of Wisconsin – Madison (May 2015, version 11) 1 Table of Contents 1.0 INTRODUCTION 3 2.0 OVERVIEW 7 3.0 ALGORITHM DESCRIPTION 8 3.1 THEORETICAL DESCRIPTION 8 3.1.1 PHYSICAL BASIS OF THE CLOUD TOP PRESSURE/TEMPERATURE/HEIGHT ALGORITHM 9 3.1.2 PHYSICAL BASIS OF INFRARED CLOUD PHASE ALGORITHM 14 3.1.3 MATHEMATICAL APPLICATION OF CLOUD TOP PRESSURE/TEMPERATURE/HEIGHT ALGORITHM 17 3.1.4 MATHEMATICAL APPLICATION OF THE CLOUD PHASE ALGORITHM 24 3.1.5 ESTIMATE OF ERRORS ASSOCIATED WITH THE CLOUD TOP PROPERTIES ALGORITHM 25 3.2 PRACTICAL CONSIDERATIONS 36 3.2.1.A RADIANCE BIASES AND NUMERICAL CONSIDERATIONS OF CLOUD TOP PRESSURE ALGORITHM 36 3.2.1.B NUMERICAL CONSIDERATIONS OF CLOUD PHASE ALGORITHM 37 3.2.2 PROGRAMMING CONSIDERATIONS OF CLOUD TOP PROPERTIES ALGORITHM 37 3.2.3 VALIDATION 37 3.2.5 EXCEPTION HANDLING 47 3.2.6.A DATA DEPENDENCIES OF CLOUD TOP PROPERTIES ALGORITHM 47 3.2.6.B DATA DEPENDENCIES OF CLOUD PHASE ALGORITHM 50 3.2.7.A LEVEL 2 OUTPUT PRODUCT OF CLOUD TOP PROPERTIES AND CLOUD PHASE ALGORITHM 50 3.2.7.B LEVEL 3 OUTPUT PRODUCT OF CLOUD TOP PROPERTIES AND CLOUD PHASE ALGORITHM 51 3.3 REFERENCES 51 4. ASSUMPTIONS 56 4.1 ASSUMPTIONS OF CLOUD TOP PROPERTIES ALGORITHM 56 4.2 ASSUMPTIONS OF IR CLOUD PHASE ALGORITHM 56 1.0 Introduction This ATBD summarizes the Collection 6 (C6) refinements in the MODIS operational cloud top properties algorithms for cloud top pressure/temperature/height and cloud thermodynamic phase.
    [Show full text]
  • Identification of the Cloud Base Height Over the Central Himalayan Region
    Atmos. Meas. Tech. Discuss., doi:10.5194/amt-2016-162, 2016 Manuscript under review for journal Atmos. Meas. Tech. Published: 13 July 2016 c Author(s) 2016. CC-BY 3.0 License. 1 Identification of the cloud base height over the central 2 Himalayan region: Intercomparison of Ceilometer and Doppler 3 Lidar 4 5 6 K.K. Shukla1, 2, K. Niranjan Kumar3, D.V. Phanikumar1, Rob K Newsom4, V. R. Kotamarthi5 7 Taha B.M.J. Ouarda3, 6 and M. Venkat Ratnam7 8 9 1Aryabhatta Research Institute of observational sciences, Nainital, India 10 2Pt. Ravishankar Shukla University, Raipur, Chhattisgarh, India 11 3Institute Center for Water and Environment, Masdar Institute of Science and Technology, Abu Dhabi, United Arab 12 Emirates 13 4Pacific Northwest National Laboratory, Richland, Washington, USA 5Argonne National Laboratory, Argonne, Illinois, USA 14 6INRS-ETE, Quebec City (Qc), Canada 15 7National Atmospheric Research Laboratory, Gadanki, Tirupati, India 16 17 Correspondence to: D V Phanikumar ([email protected]; [email protected]) 18 19 Abstract. We present the measurement of cloud base height (CBH) derived from the Doppler Lidar (DL), 20 Ceilometer (CM) and Moderate Resolution Imaging Spectroradiometer (MODIS) satellite over a high altitude 21 station in the central Himalayan region for the first time. We analyzed six cases of cloud overpass during the 22 daytime convection period by using the cloud images captured by total sky imager. The occurrence of thick clouds 23 (> 50%) over the site is more frequent than thin clouds (< 40 %). In every case, the CBH indicates less than 1.2 km, 24 above ground level (AGL) observed by both DL and CM instruments.
    [Show full text]
  • Observation of Clouds
    CHAPTER CONTENTS Page CHAPTER 15. OBSERVATION OF CLOUDS ........................................... 465 15.1 General ................................................................... 465 15.1.1 Definitions ......................................................... 465 15.1.2 Units and scales ..................................................... 466 15.1.3 Meteorological requirements ......................................... 466 15.1.4 Observation and measurement methods ............................... 467 15.1.4.1 Cloud amount .............................................. 467 15.1.4.2 Cloud-base height. 467 15.1.4.3 Cloud type ................................................. 467 15.2 Estimation and observation of cloud amount, cloud-base height and cloud type by human observer .................................................... 468 15.2.1 Making effective estimations .......................................... 468 15.2.2 Estimation of cloud amount ........................................... 468 15.2.3 Estimation of cloud-base height ....................................... 468 15.2.4 Observation of cloud type ............................................ 469 15.3 Instrumental measurements of cloud amount .................................. 470 15.3.1 Using a laser ceilometer .............................................. 470 15.3.2 Using a pyrometer ................................................... 471 15.3.3 Using a sky camera .................................................. 471 15.4 Instrumental measurement of cloud-base height ...............................
    [Show full text]
  • Cloud Classifications and Characteristics
    By Ted Funk Science and Operations Officer Cloud Classifications and Characteristics Clouds are classified according to their height above and appearance (texture) from the ground. The following cloud roots and translations summarize the components of this classification system: 1) Cirro-: curl of hair, high; 2) Alto-: mid; 3) Strato-: layer; 4) Nimbo-: rain, precipitation; and 5) Cumulo-: heap. Cirrus clouds (above) High-level clouds: High-level clouds occur above about 20,000 feet and are given the prefix “cirro.” Due to cold tropospheric temperatures at these levels, the clouds primarily are composed of ice crystals, and often appear thin, streaky, and white (although a low sun angle, e.g., near sunset, can create an array of color on the clouds). The three main types of high clouds are cirrus, cirrostratus, and cirrocumulus. Cirrus clouds are wispy, feathery, and composed entirely of ice crystals. They often Cirrostratus clouds (above) are the first sign of an approaching warm front or upper-level jet streak. Unlike cirrus, cirrostratus clouds form more of a widespread, veil-like layer (similar to what stratus clouds do in low levels). When sunlight or moonlight passes through the hexagonal- shaped ice crystals of cirrostratus clouds, the light is dispersed or refracted (similar to light passing through a prism) in such a way that a familiar ring or halo may form. As a warm front approaches, cirrus clouds tend to thicken into cirrostratus, which may, in turn, thicken and lower into altostratus, stratus, and even nimbostratus. Cirrocumulus clouds (above) Finally, cirrocumulus clouds are layered clouds permeated with small cumuliform lumpiness.
    [Show full text]
  • Atmospheric Moist Convection
    Atmospheric moist convection Peter Bechtold Research Department March 2009 – last revised 4 March 2019 Atmospheric Moist Convection Table of Contents PREFACE ................................................................................................................................................................. 4 1 THE NATURE OF MOIST CONVECTION ................................................................................................... 5 1.1 INTRODUCTION .................................................................................................................................................. 5 1.2 TROPICAL METEOROLOGY AND CLIMATE .......................................................................................................... 6 1.2.1 Precipitation and radiative convective equilibrium ...................................................................................... 7 1.2.2 Cloud distributions ....................................................................................................................................... 8 1.3 TROPICAL CIRCULATIONS ................................................................................................................................ 10 1.3.1 The Hadley and Walker circulation ............................................................................................................ 10 1.3.2 Tropical Waves ........................................................................................................................................... 11 1.3.3 The
    [Show full text]