DOCSLIB.ORG

Summer 2018 Astron 9 Week 2 FINAL

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text

Load more

ORDER OF MAGNITUDE PHYSICS

RICHARD ANANTUA, JEFFREY FUNG AND JING LUAN
WEEK 2: FUNDAMENTAL INTERACTIONS, NUCLEAR AND ATOMIC PHYSICS

REVIEW OF BASICS

• Units

• Systems include SI and cgs • Dimensional analysis must confirm units on both sides of an equation match

• BUCKINGHAM’S PI THEOREM - For a physical equation involving N variables, if there are R independent dimensions, then there are N-R independent dimensionless groups, denoted Π", …, Π%&'.

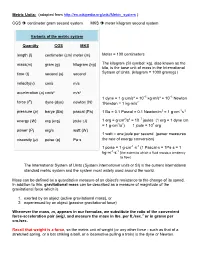
UNITS REVIEW – BASE UNITS

• Physical quantities may be expressed using several choices of units • Unit systems express physical quantities in terms of base units or combinations thereof

Quantity

Length

  • SI (mks)
  • Gaussian (cgs)

Centimeter (cm) Gram (g)

Imperial

  • Meter (m)
  • Foot (ft)

  • Mass
  • Kilogram (kg)

Second (s) Kelvin (K)
Pound (lb) Second (s) Farenheit (ºF)

  • Time
  • Second (s)

Temperature Luminous intensity Amount
Kelvin (K)*
Candela (cd) Mole (mol) Ampere (A)
Candela (cd)* Mole (mol)*
Current

* Sometimes not considered a base cgs unit

REVIEW – DERIVED UNITS

• Units may be derived from others

Quantity

Momentum Force

  • SI
  • cgs

  • kg m s-1
  • g cm s-1

Newton N=kg m s-2 Joule J=kg m2 s-2 Watt J=kg m2 s-3 dyne dyn=g cm s-2 erg=g cm2 s-2 erg/s=g cm2 s-3
Energy Power

  • Pressure
  • Pascal Pa=kg m-1 s-2 barye Ba=g cm-1 s-2

• Some unit systems differ in which units are considered fundamental

  • Electrostatic Units
  • SI (mks)
  • Gaussian cgs

(cm3 g s-2)1/2 (cm3 g s-4)1/2

  • Charge
  • A s

  • A
  • Current

REVIEW – UNITS

• The cgs system for electrostatics is based on the assumptions kE=1, kM =2kE/c2

• EXERCISE: Given the Gaussian cgs unit of force is g cm s-2, what is the electrostatic unit of charge?

2

#

)/+

= g cm/ s1+ )/+

2

  • ! =
  • ⟹ # = ! &

[&]2

REVIEW – BUCKINGHAM’S PI THEOREM

• BUCKINGHAM’S PI THEOREM - For a physical equation involving N variables, if there are R independent dimensions, then there are N-R independent dimensionless groups, denoted Π", …, Π%&'.

• EXERCISE: What are the units of f(Π", …, Π%&')?

• We can write f(Π , …, Π )=C for dimensionless constant C

  • "
  • %&'

• EXERCISE: What variables are relevant for the drag force on a marble falling slowly through honey?

• Drag force Fd, Viscosity (, radius R, speed v, fluid density ρ

*+

FUNDAMENTAL PARTICLES AND INTERACTIONS

• “Atomic” concept and origins • Hierarchy of scales • Standard Model of particle physics

• Nuclear physics • Atomic physics

ICEBREAKER – PHYSICS 2 TRUTHS AND A LIE

• Make 2 true statements and 1 false statement

• 1 statement must be about yourself • 1 statement must be about your home institution • 1 statement must be about physics

HISTORY OF THE “ATOM”

• Ancient Greeks believed that matter is infinitely and continuously divisible until the advent of the Atomism

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomism:

• Matter ultimately consists of “atoms” or unchanging discrete particles

ATOMIC MODEL - HISTORY

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomic (Discrete) Matter • John Dalton (1766-1844) – Atomic Chemistry

LAW OF MULTIPLE PROPORTIONS:
If Elements A and B can form Compounds 1, 2, 3 … ,

then for a fixed mass of A, the masses of B occurring in different compounds form ratios of integers form

ATOMIC MODEL - HISTORY

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomic (Discrete) Matter • John Dalton (1766-1844) – Atomic Chemistry

  • Compound
  • Tin
  • Tin

• EXERCISE: Tin and oxygen form the following compounds:

  • oxide
  • dioxide

Percentage of mass 88.1% from tin
78.7%
Percentage of mass 11.9% from oxygen
21.3%

For 100g of tin, how much oxygen is needed to make 1.) tin oxide, 2.) tin dioxide?

100g

1. ) Oxygen in tin oxide =

.119 = 13.51g
.881 100g

2.) Oxygen in tin dioxide =

.213 = 27.06g
.787

ATOMIC MODEL - HISTORY

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomic (Discrete) Matter • John Dalton (1766-1844) – Atomic Chemistry

1. Matter is comprised of small, but finite-sized atoms 2. All atoms of a given element are identical 3. Atoms cannot be destroyed 4. Compounds are formed by combining atoms in ratios of whole numbers 5. Chemical reactions are rearrangements of atoms

CHARGE CONCEPT AND HISTORY

• The Greeks also knew when certain materials (for example, amber (elektron)) were rubbed, a force could make some attract and some repel.

• William Gilbert (1544-1603) – wrote De Magnete, in which he coined
“electrius” (of amber) to describe attractive properties of charged materials

ATOMIC MODEL - HISTORY

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomic (Discrete) Matter • John Dalton (1766-1844) – Atomic Chemistry • Joseph Thomson (1856-1940) – Discovered negative “corpuscles” accelerated enough in cathode ray tubes to suggest they were 2000x lighter than H atoms

Plum Pudding Model: Electrons thought to be small negative charges immersed in the positive interior of an atom

• Thompson used electric plates and magnets in cathode ray tubes to determine e/me

ATOMIC MODEL - HISTORY

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomic (Discrete) Matter • John Dalton (1766-1844) – Atomic Chemistry • Joseph Thomson (1856-1940) – Plum Pudding Model of Atom

• Exercise: Combine fundamental constants ! , e, % and & for the electron and photon into a

  • "
  • "

length scale, i.e., the classical electron radius

[)] +
[-],
[3] +
[5],

67 "8
97

+

67 "8 97 :8

,

  • 4
  • 4

,

2

  • !" =
  • ⟹ !"/ = 0 1 =
  • ⟹
  • =
  • ⟹
  • = [1]

,

5

!"/, %"&,

8.99 ? 10BN ? m,/C, 1.60 ? 10EFBC, ,

  • ; =
  • =
  • = 2.80 ⋅ 10EFN
  • m

"

9.11 ⋅ 10E4Fkg 3.00 ⋅ 10Km/s

,

ATOMIC MODEL - HISTORY

• Democritus (ca. 460B.C.-370B.C.) – Theory of Atomic (Discrete) Matter • John Dalton (1766-1844) – Atomic Chemistry • Joseph Thomson (1856-1940) – Plum Pudding Model of Atom • Ernest Rutherford (1871-1937) – Fired positive !-particles at a few atoms thick gold foil sheet, and some recoiled backwards (imagine a cannonball recoiling from tissue)

• Exercise: What would be the mass of a H atom if the nucleus were filled without empty space all the way up to the electron and were the size of a marble?

+
+

  • *
  • 1045m

#$%&'( +

  • "
  • =
  • "0 ≈
  • + 10459kg = 10<kg

#$%&'(

10478

m
*

,-.'(-/

HIERARCHY OF SCALES

• Modern physics spans an astounding range of scales from quantum to cosmological

Observable
?e-

?

Galaxy

?
?
Universe

m

10-35

10-14

  • 1
  • ?

HIERARCHY OF SCALES

• Modern physics spans an astounding range of scales from quantum to cosmological

Observable e-

Galaxy

1021

Strings

10-35

Nucleus

10-14

Universe

m

10-15

1

1027

HIERARCHY OF SCALES

• Length scales can be associated with momenta via the de Broglie relation

!" = ℎ, ℎ = 6.63 ) 10,-.J ) s = 4.12 ) 10,23 eV ) s

• Rest mass can be associated with an energy scale via 4 = 869

45 = ℎ6/!

• Photon energy is related to wavelength via

Infrared Photon

UV
Radio

Photon

Planck Energy
Baryonic Acoustic Oscillation

Higgs Boson

Proton e-

Photon
Energy
1028eV
?

?

0.1TeV ?

?

0.1 eV
?

HIERARCHY OF SCALES

• Length scales can be associated with momenta via the de Broglie relation

'* = ℎ, ℎ = 6.63 / 10234J / s = 4.12 / 10289 eV / s

• Rest mass can be associated with an energy scale via ! = (%)

!" = ℎ%/'

• Photon energy is related to wavelength via

Infrared Photon

UV
Radio

Photon

Planck Energy
Baryonic Acoustic Oscillation

Higgs Boson

Proton e-

Photon
Energy

1028eV
Sound wave, not light

150 Mpc

  • 0.5MeV
  • 0.1 eV

0.1TeV GeV

1 neV

(1 km)
0.1 keV

(10-8 m) (10-5 m)

UNIFICATION IN PHYSICS

• Einstein unified inertial and accelerating reference frames in the general theory of relativity

• In electromagnetism, special relativity shows us electricity and magnetism are two sides of the same coin
• Other interactions in physics have been shown or predicted to be unified

ORDER OF MAGNITUDE PHYSICS

RICHARD ANANTUA, JEFFREY FUNG AND JING LUAN
WEEK 2: FUNDAMENTAL INTERACTIONS, NUCLEAR AND ATOMIC PHYSICS

REVIEW

• List these events in chronological order and name relevant scientists: Gold Foil
Experiment, Plum Pudding Model, Atomism, Law of Multiple Proportions

• Atomism (Democritus), Law of Multiple Proportions (Dalton), Plum Pudding Model (Thomson),
Gold Foil Experiment (Rutherford)

• Arrange the following in order of increasing energy needed to produce in a particle accelerator: string, electron, proton.

• Electron, proton, string

• Two Truths and a Lie

• ____ hates physics • Daulande doesn’t have a ____

REVIEW

• List these events in chronological order and name relevant scientists: Gold Foil
Experiment, Plum Pudding Model, Atomism, Law of Multiple Proportions

• Atomism (Democritus), Law of Multiple Proportions (Dalton), Plum Pudding Model (Thomson),
Gold Foil Experiment (Rutherford)

• Arrange the following in order of increasing energy needed to produce in a particle accelerator: string, electron, proton.

• Electron, proton, string

• Two Truths and a Lie

• Arthur hates physics • Daulande doesn’t have a ____

REVIEW

• List these events in chronological order and name relevant scientists: Gold Foil
Experiment, Plum Pudding Model, Atomism, Law of Multiple Proportions

• Atomism (Democritus), Law of Multiple Proportions (Dalton), Plum Pudding Model (Thomson),
Gold Foil Experiment (Rutherford)

• Arrange the following in order of increasing energy needed to produce in a particle accelerator: string, electron, proton.

• Electron, proton, string

• Two Truths and a Lie

• Arthur hates physics • Daulande doesn’t have a goldfish

STANDARD MODEL OF PARTICLE PHYSICS

• The Standard Model is currently comprised of

• (Integer+1/2)-spin fermions and integer-spin bosons • 3 generations of fermions • Electromagnetic, weak and strong gauge bosons

• Fermions (but not bosons) obey the

• PAULI EXCLUSION PRINCIPLE – no two half-spin particles can occupy the same quantum state

QUARKS MULTIPLETS

• Hadrons are combinations of quarks “glued” together by gluons via strong interaction

  • "
  • #

• Mesons, such as ! and ! , are quark doublets • Baryons, such as p and n, are quark triples

Q=? s=?
Q=? s=?
Q=? s=?
Q=? s=?

• Quarks may exist in combinations of 5’s known as pentaquarks • Leptons, such as electrons and muons, have no quark substructure and do not partake in the strong interaction

QUARKS MULTIPLETS

• Hadrons are combinations of quarks “glued” together by gluons via strong interaction

  • "
  • #

• Mesons, such as ! and ! , are quark doublets • Baryons, such as p and n, are quark triples

  • Q=1
  • Q=-1

s=0
Q=1 s=1/2
Q=0 s=1/2

• Quarks may exist in combinations of 5’s known ass=p0entaquarks • Leptons, such as electrons and muons, have no quark substructure and do not partake in the strong interaction

SPONTANEOUS SYMMETRY BREAKING

• Feynman devised diagrams modeling forces (electromagnetic, weak and strong) as interactions mediated by exchange particles

• Photons carry the electromagnetic force • W and Z bosons carry the weak force

t
Richard Feynman 1918-1988

• Gluons carry the strong force • At high energy, symmetry emerges among

E

force-carrying Goldstone bosons
• Many low energy states available to break

symmetry

UNIFICATION IN PHYSICS

• Einstein unified inertial and accelerating reference frames in the general theory of relativity
• In electromagnetism, special relativity shows us electricity and magnetism are two sides of the same coin
• At the electroweak energy scale (246 GeV), the electromagnetic force is

indistinguishable from the weak force
• At the strong-electroweak scale, the electroweak force is predicted by grand unified

theory to be indistinguishable from the strong force. Proton decay detectors such as super Kamiokande have yet to confirm this prediction

Recommended publications
  • Mercury Barometers and Manometers

    Mercury Barometers and Manometers

    NBS MONOGRAPH 8 Mercuiy Barometers and Manometers U.S. DEPARTMENT OF COMMERCE NATIONAL BUREAU OF STANDARDS THE NATIONAL BUREAU OF STANDARDS Functions and Activities The functions of the National Bureau of Standards are set forth in the Act of Congress, March 3, 1901, as amended by Congress in Public Law 619, 1950. These include the development and maintenance of the national standards of measurement and the provision of means and methods for making measurements consistent with these standards; the determination of physical constants and properties of materials; the development of methods and instruments for testing materials, devices, and structures; advisory services to government agencies on scientific and technical problems; in- vention and development of devices to serve special needs of the Government; and the development of standard practices, codes, and specifications. The work includes basic and applied research, development, engineering, instrumentation, testing, evaluation, calibration services, and various consultation and information services. Research projects are also performed for other government agencies when the work relates to and supplements the basic program of the Bureau or when the Bureau's unique competence is required. The scope of activities is suggested by the listing of divisions and sections on the inside of the back cover. Publications The results of the Bureau's work take the form of either actual equipment and devices or pub- lished papers. These papers appear either in the Bureau's own series of publications or in the journals of professional and scientific societies. The Bureau itself publishes three periodicals available from the Government Printing Office: The Journal of Research, published in four separate sections, presents complete scientific and technical papers; the Technical News Bulletin presents summary and pre- liminary reports on work in progress; and Basic Radio Propagation Predictions provides data for determining the best frequencies to use for radio communications throughout the world.
  • Alkali Metal Vapor Pressures & Number Densities for Hybrid Spin Exchange Optical Pumping

    Alkali Metal Vapor Pressures & Number Densities for Hybrid Spin Exchange Optical Pumping

    Alkali Metal Vapor Pressures & Number Densities for Hybrid Spin Exchange Optical Pumping Jaideep Singh, Peter A. M. Dolph, & William A. Tobias University of Virginia Version 1.95 April 23, 2008 Abstract Vapor pressure curves and number density formulas for the alkali metals are listed and compared from the 1995 CRC, Nesmeyanov, and Killian. Formulas to obtain the temperature, the dimer to monomer density ratio, and the pure vapor ratio given an alkali density are derived. Considerations and formulas for making a prescribed hybrid vapor ratio of alkali to Rb at a prescribed alkali density are presented. Contents 1 Vapor Pressure Curves 2 1.1TheClausius-ClapeyronEquation................................. 2 1.2NumberDensityFormulas...................................... 2 1.3Comparisonwithotherstandardformulas............................. 3 1.4AlkaliDimers............................................. 3 2 Creating Hybrid Mixes 11 2.1Predictingthehybridvaporratio.................................. 11 2.2Findingthedesiredmolefraction.................................. 11 2.3GloveboxMethod........................................... 12 2.4ReactionMethod........................................... 14 1 1 Vapor Pressure Curves 1.1 The Clausius-Clapeyron Equation The saturated vapor pressure above a liquid (solid) is described by the Clausius-Clapeyron equation. It is a consequence of the equality between the chemical potentials of the vapor and liquid (solid). The derivation can be found in any undergraduate text on thermodynamics (e.g. Kittel & Kroemer [1]): Δv · ∂P = L · ∂T/T (1) where P is the pressure, T is the temperature, L is the latent heat of vaporization (sublimation) per particle, and Δv is given by: Vv Vl(s) Δv = vv − vl(s) = − (2) Nv Nl(s) where V is the volume occupied by the particles, N is the number of particles, and the subscripts v & l(s) refer to the vapor & liquid (solid) respectively.
  • 3.1 Dimensional Analysis

    3.1 Dimensional Analysis

    3.1 DIMENSIONAL ANALYSIS Introduction (For the Teacher).............................................................................................1 Answers to Activities 3.1.1-3.1.7........................................................................................8 3.1.1 Using appropriate unit measures..................................................................................9 3.1.2 Understanding Fundamental Quantities....................................................................14 3.1.3 Understanding unit definitions (SI vs Non-sI Units)................................................17 3.1.4 Discovering Key Relationships Using Fundamental Units (Equations)...................20 3.1.5 Using Dimensional Analysis for Standardizing Units...............................................24 3.1.6 Simplifying Calculations: The Line Method.............................................................26 3.1.7 Solving Problems with Dimensional Analysis ..........................................................29 INTRODUCTION (FOR THE TEACHER) Many teachers tell their students to solve “word problems” by “thinking logically” and checking their answers to see if they “look reasonable”. Although such advice sounds good, it doesn’t translate into good problem solving. What does it mean to “think logically?” How many people ever get an intuitive feel for a coluomb , joule, volt or ampere? How can any student confidently solve problems and evaluate solutions intuitively when the problems involve abstract concepts such as moles, calories,
  • Thermodynamics

    Thermodynamics

    Thermodynamics D.G. Simpson, Ph.D. Department of Physical Sciences and Engineering Prince George’s Community College Largo, Maryland Spring 2013 Last updated: January 27, 2013 Contents Foreword 5 1WhatisPhysics? 6 2Units 8 2.1 SystemsofUnits....................................... 8 2.2 SIUnits........................................... 9 2.3 CGSSystemsofUnits.................................... 12 2.4 British Engineering Units . 12 2.5 UnitsasanError-CheckingTechnique............................ 12 2.6 UnitConversions...................................... 12 2.7 OddsandEnds........................................ 14 3 Problem-Solving Strategies 16 4 Temperature 18 4.1 Thermodynamics . 18 4.2 Temperature......................................... 18 4.3 TemperatureScales..................................... 18 4.4 AbsoluteZero........................................ 19 4.5 “AbsoluteHot”........................................ 19 4.6 TemperatureofSpace.................................... 20 4.7 Thermometry........................................ 20 5 Thermal Expansion 21 5.1 LinearExpansion...................................... 21 5.2 SurfaceExpansion...................................... 21 5.3 VolumeExpansion...................................... 21 6Heat 22 6.1 EnergyUnits......................................... 22 6.2 HeatCapacity........................................ 22 6.3 Calorimetry......................................... 22 6.4 MechanicalEquivalentofHeat............................... 22 7 Phases of Matter 23 7.1 Solid............................................
  • CONVERSION ANYTHING – Readme

    CONVERSION ANYTHING – Readme

    CONVERSION ANYTHING – Readme 1. Package Overview This package performs the following: ・ Converting Measurement Unit - After receiving value and type of Unit, ConversionAnything will calculate and provide values of equivalent units in the same category within a short time. - Recently, this package is able to provide 10 different categories of measurement ・Converting Currencies - After receiving base currency, ConversionAnything will access European Central Bank’s server and return the lastest exchange rates of all currencies that are available. - In case Bot requires ConversionAnything to provides exchange rates in a specific date, ConversionAnything will follow the requirement and return the exact historical rates that are - At the moment, this package can exchange among 30 strongest currencies in the world. 2. Activities List No Activities Description 1 Convert Length Converting between different length unit. 2 Convert Speed Converting between different speed unit. 3 Convert Mass Converting between different mass unit. 4 Convert Temperature Converting between different temperature unit. 5 Convert Angle Converting between different angle unit. 6 Convert Area Converting between different area unit. 7 Convert Time Converting between different time unit. 8 Convert DataStorage Converting between different data unit. 9 Convert Pressure Converting between different pressure unit. 10 Convert Volume Converting between different length unit. 11 Convert DataTransferRate Converting between different data transfer rate unit. 12 Convert Currencies Converting between different currencies. 13 Convert Currencies By Date Converting between different currencies by date. 3. Activities Detail 3.1 Convert Length ・Input description Input Description From Unit Current unit of length. From Value Value to convert. To Unit Unit want to convert. Round The number of fractional digits in the return value.
  • Life and Works of Antoine Louis Barye Sculptor with Eighty-Six Wood-Cuts

    Life and Works of Antoine Louis Barye Sculptor with Eighty-Six Wood-Cuts

    LIFE A ND WORKS OF A NTOINE L O UIS BA R YE SCULPTOR WITH EIGHTY- SIX WO OD - CUTS A R TO TYPES A ND PRINTS IN MEMOR Y OF A N EX HIBITION OF HIS ‘ BR ONZ ES PA INTINGS A ND WA TER - COL ORS HELD A T NE W YORK IN A ID OF THE FUND FOR HIS MONUMENT A T PA RIS WRITTEN B Y CHA RLES D E K A Y PUBLISHED B Y THE BA R YE MONUMENT A SSO CIA TION A T NE W YORK IN NO VEMBER OF M D C C C L X X X IX CHARLE S Tu e DEWNNE Pases . THE AUTHOR D ED ICATES THIS VOLUME TO WILLIAM THOMPSON WALTERS FIRST TO HONOR THE GENIUS OF ANTOINE LOUIS BARYE WITH BRONZ ES ERECTED IN AMERICA FOREMOST OF THOSE WH O WOULD RAISE HIS MONUMENT ON THE SEINE 84 . O RC . No . F E St one G rou p on th e Lou vre . A NOTE IN PREFA CE France has writers and critics so many and so able that it seems pre n m n u ne h r ma te Yet how ten do su mptu ou s i an A erica to disc ss o of e s rs . of we not find the view taken by a foreigner more su ggestive than the opini ons of a fellow-cou ntryman A great artist may be regarded throu gh variou s acet wh ch the one ma be not le s tru e than the the .
  • Engilab Units 2018 V2.2

    Engilab Units 2018 V2.2

    EngiLab Units 2021 v3.1 (v3.1.7864) User Manual www.engilab.com This page intentionally left blank. EngiLab Units 2021 v3.1 User Manual (c) 2021 EngiLab PC All rights reserved. No parts of this work may be reproduced in any form or by any means - graphic, electronic, or mechanical, including photocopying, recording, taping, or information storage and retrieval systems - without the written permission of the publisher. Products that are referred to in this document may be either trademarks and/or registered trademarks of the respective owners. The publisher and the author make no claim to these trademarks. While every precaution has been taken in the preparation of this document, the publisher and the author assume no responsibility for errors or omissions, or for damages resulting from the use of information contained in this document or from the use of programs and source code that may accompany it. In no event shall the publisher and the author be liable for any loss of profit or any other commercial damage caused or alleged to have been caused directly or indirectly by this document. "There are two possible outcomes: if the result confirms the Publisher hypothesis, then you've made a measurement. If the result is EngiLab PC contrary to the hypothesis, then you've made a discovery." Document type Enrico Fermi User Manual Program name EngiLab Units Program version v3.1.7864 Document version v1.0 Document release date July 13, 2021 This page intentionally left blank. Table of Contents V Table of Contents Chapter 1 Introduction to EngiLab Units 1 1 Overview ..................................................................................................................................
  • Units of Measure

    Units of Measure

    Units of Measure Units marked with asterisks are base, derived, or supplementary units of the Systeme International. Unit Abbreviation abampere - spell out abohm - spell out abvolt - spell out amagat - spell out *ampere - A ampere hour - A h ampere turns per meter - At/m angstrom - Å arc minute - arc min astronomical unit - AU atmosphere - atm atmosphere, standard - As atomic mass unit - u atomic parts per million - at. ppm atomic percent - at. % atomic time unit - atu atomic unit- a.u. attofarad - aF bar - spell out bark - spell out barn - b barye - spell out biot - Bi bit or bits - spell out blobs per hundred microns - blobs/(100 um) bohr - spell out British thermal unit - Btu bytes - spell out calorie - cal *candela - cd candelas per square meter - cd/m2 candlepower - cp centimeter - cm centipoise - cP *coulomb - C counts per minute - counts/min, cpm counts per second - counts/s cubic centimeter - cm3, (cc not rec.) curie - Ci cycle - spell out, c cycles per second - cps, c/s day d, - or spell out debye - D decibel - dB, dBm degree - [ring], deg degrees - Baumé [ring]B degrees - Celsius (centigrade) [ring]C degrees - Fahrenheit [ring]F degrees - Kelvin K disintegrations per minute - dis/min disintegrations per minute per microgram - dis/min ug disintegrations per second - dis/s dyne - dyn electromagnetic unit - emu electron barn - eb electrons per atom - e/at. electrons per cubic centimeter - e/cm3, e/cc, e cm-3 electron unit - e.u. electron volt - eV electrostatic unit - esu entropy unit - eu erg - spell out *farad - F femtofarad - fF femtometer - fm fermi - F fissions per minute - fpm foot - ft foot-candle - fc foot-lambert - fL foot-pound - ft lb formula units - f.u.
  • Metric Units.Pdf

    Metric Units.Pdf

    Metric Units: (adapted from http://en.wikipedia.org/wiki/Metric_system ) CGS centimeter gram second system MKS meter kilogram second system Variants of the metric system Quantity CGS MKS length (l) centimeter (cm) meter (m) Meter = 100 centimeters mass(m) gram (g) kilogram (kg) The kilogram (SI symbol: kg), also known as the kilo, is the base unit of mass in the International time (t) second (s) second System of Units. (kilogram = 1000 gram(g) ) velocity(v) cm/s m/s acceleration (a) cm/s² m/s² 1 dyne = 1 g·cm/s² = 10−5 kg·m/s² = 10−5 Newton force (F) dyne (dyn) newton (N) 1Newton = 1 kg·m/s2 pressure (p) barye (Ba) pascal (Pa) 1 Ba = 0.1 Pascal = 0.1 Newton/m2 = 1 g·cm-1s-2 2 2 −7 energy (W) erg (erg) joule (J) 1 erg = g·cm /s = 10 joules (1 erg = 1 dyne cm = 1 g·cm2/s2) 1 joule = 107 erg power (P) erg/s watt (W) 1 watt = one joule per second (power measures viscosity (µ) poise (p) Pa·s the rate of energy conversion) 1 poise = 1 g·cm-1·s-1 (1 Pascal·s = 1Pa·s = 1 -1 -1 kg·m ·s (the extent to which a fluid resists a tendency to flow) The International System of Units (System international units or SI) is the current international standard metric system and the system most widely used around the world. Mass can be defined as a quantitative measure of an object's resistance to the change of its speed.
  • Supernova Light Curves and Spectra Lecture Notes for Lessons 4-8 for “Stellar Explosions”, TUM, 2017

    Supernova Light Curves and Spectra Lecture Notes for Lessons 4-8 for “Stellar Explosions”, TUM, 2017

    Supernova light curves and spectra Lecture notes for lessons 4-8 for “Stellar explosions”, TUM, 2017 Anders Jerkstrand [email protected] Overview 51 A CCSN explosion deposits an energy Edep 10 erg in the core of the star. This energy is spread to the whole star by∼ a shock wave propagating with 4 −1 v 10 kms . It reaches the surface after a time t = R0/v , shock ∼ surf shock where R0 is the stellar radius. We can estimate t 1 minute for R0 =1 R⊙, surf ∼ tsurf 1 day for R0 = 500 R⊙ (Red SuperGiant (RSG)). This begins the light display∼. Equipartition. In the limit of strong shocks (vshock vsound), one can show that radiation-dominated gas fulfills equipartition: ≫ 1 E0 = E0 = E (1) int kin 2 dep I.e., in the shock wake, energy is equally divided between internal random energy and bulk kinetic energy (as the layers are both accelerated and heated). This limit is a good approximation for SNe (v 10 kms−1). sound ∼ Basic physics of the fireball The first law of thermodynamics states that “the change in internal energy equals energy deposited, minus (net) energy transported out, minus work done (pdV)”. For a moving gas we write this law on Lagrangian (comoving) form, where m is he coordinate rather than x or v: δe (m,t) ∂L(m,t) ∂ (1/ρ(m,t)) int = s(m,t) p(m,t) (2) δt − ∂m − ∂t −1 Here eint is the internal energy per unit mass (erg g ), s is the energy injection per unit mass and time (erg s−1 g−1), L is the luminosity (erg s−1), p is pressure (barye =dyne cm−2 = erg cm−3), and ρ is the density (g cm−3).
  • Quantum Mechanics Pressure

    Quantum Mechanics Pressure

    Quantum Mechanics_Pressure Pressure Common symbols P SI unit Pascal (Pa) In SI base units 1 kg/(m·s2) Derivations from other quantities P = F / A Pressure as exerted by particle collisions inside a closed container. Pressure (symbol: P or p) is the ratio of force to the area over which that force is distributed. Pressure is force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure (also spelled gagepressure)[a] is the pressure relative to the local atmospheric or ambient pressure. Pressure is measured in any unit of force divided by any unit of area. The SI unit of pressure is thenewton per square metre, which is called thePascal (Pa) after the seventeenth-century philosopher and scientist Blaise Pascal. A pressure of 1 Pa is small; it approximately equals the pressure exerted by a dollar bill resting flat on a table. Everyday pressures are often stated in kilopascals (1 kPa = 1000 Pa). Definition Pressure is the amount of force acting per unit area. The symbol of pressure is p.[b][1] Formula Conjugate variables of thermodynamics Pressure Volume (Stress) (Strain) Temperature Entropy Chemical potential Particle number Mathematically: where: is the pressure, is the normal force, is the area of the surface on contact. Pressure is a scalar quantity. It relates the vector surface element (a vector normal to the surface) with the normal force acting on it. The pressure is the scalarproportionality constant that relates the two normal vectors: The minus sign comes from the fact that the force is considered towards the surface element, while the normal vector points outward.
  • AIP Style Manual Was Followed by a Second Than Has Been the Case with the Previous Editions

    AIP Style Manual Was Followed by a Second Than Has Been the Case with the Previous Editions

    STYLE MANUAL Fourth Edition Prepared under the Direction of the AIP Publication Board Searchable version provided with permission by Ken Hanson; home page http://public.lanl.gov/kmh/ American institute of Physics New York Copyright @ 1990 American lnstitute of Physics, Inc. This book, or parts thereof, may not be reproduced in any form without permission. Library of Congress Catalog Card Number 89-81194 InternationalStandard Book Number 0-88318-642-X American lnstitute of Physics 500 Sunnyside Blvd. Woodbury, NY I1797 AIP Pub. R-283.2 Printed in the United States of America First edition, 1951 Second edition, 1959; revisions 1963,1965, 1967,1968,1969,1970,1973 Third edition, 1978 Fourth edition, 1990 fifth printing, 1997 Preface The American Institute of Physics published its first At the time of the third edition ( 1978 ) the text pages of Style Manual in 195 1. It was produced at the request of the many AIP and Member Society journals were composed by Publication Board, which was made up of the editors of all typewriter, because the monotype composition used earlier Member Society journals, and with their approval. had become too expensive. Since then practically all journal At that time there were five Member Societies, each pages have been produced by computer-controlled photo- publishing one or two journals through the services provided composition, and at the present time a second generation of by the Institute. Now there are ten Member Societies, which computer typesetting systems is coming into use. The next between them publish about forty archival journals and sev- steps, which will be made possible by this new typesetting en translated journals.