DOCSLIB.ORG

Ionic Basis of Resting and Action Potentials. In: Comprehensive

Total Page：16

File Type：pdf, Size：1020Kb

Download full-text PDF Read full-text
Ionic Basis of Resting and Action Potentials. In: Comprehensive CHAPTER 4 Ionic basis of resting and action potentials Department of Physiology and Biophysics, University of Washington BERTIL HILLE I School of Medicine, Seattle, Washington CHAPTER CONTENTS Diffusion of charged particles in electric field Nernst-Planck equations Goldman-Hodgkin-Katz equation Development of Membrane Theory Ussing flux ratio Before intracellular recording Origins Independence relation Stimulation Eyring rate theory Conduction Practical calculations Cable Impedance First intracellular recordings from squid giant axons Resting potential Action potential EXCITABLE CELLS like other cells are completely sur- Afterpotential rounded by a thin unit membrane. Excitation of ex- Direct Measurement of Ionic Currents in Axon Membranes citable cells is always accompanied by changes in the Voltage-clamp method membrane potential. These changes may be abrupt Electrochemical separation of ionic currents Ion substitution experiments or slow, brief or long lasting, depending on the cell Reversal of current at Nernst potential and the stimulus, but the mechanisms of potential Tracer flux measurement change are fundamentally the same. They always Potassium current involve a change in the permeability of the mem- Pharmacological separation of ionic currents brane to ions. The guiding principles, called the Selective block Separate channels membrane theory or ionic hypothesis, may be stated Hodgkin-Huxley Model as follows: potentials a) develop across unit mem- Quantitative analysis ofl,,, and I, branes, b) depend on ionic concentration differences, Ionic conductances and c) arise because the membrane is selectively Hodgkin-Huxley equations Calculations with Hodgkin-Huxley model permeable to some ions. A corollary of these princi- Variety of Excitable Cells ples is that electric current flowing across mem- Myelinahd nerve branes is carried by the movement of ions. This chap- Saltatory conduction ter describes the electric phenomena of excitability, Ionic basis particularly as seen in axons, and shows how the Other axons Cell bodies potentials and currents at rest and during activity Gastropod ganglia may be analyzed and explained by the ionic hypothe- Vertebrate cell bodies sis. The approach is first historical, tracing the early Muscle development and first tests of the ionic hypothesis on Ionic Channels Sodium channels squid giant axons, then broadens to deal with the Number of channels modern consolidation of facts in many tissues, and Ionic selectivity concludes with derivations of some of the fundamen- Gating tal equations used to describe membrane potentials Potassium channels Long pore and ion fluxes. Some familiarity with classic proper- Ionic selectivity ties of excitable cells and the cable properties of axons Gating is assumed (see the chapter by Rall in this Hand- Calcium channels book). Specific applications of the ionic hypothesis to Equations of Ionic Hypothesis muscles, synapses, and sensory receptors are found in Solving Hodgkin-Huxley model Empirical constants other chapters in this Handbook. Solutions Significant features of membrane excitation can be seen by recording electric potential variations with The author’s original work was supported by grant NS 08174 an intracellular electrode. By convention the mem- from the National Institutes of Health. brane potential is defined as inside minus outside 99 100 HANDBOOK OF PHYSIOLOGY 8 THE NERVOUS SYSTEM I potential. The recorded potential suddenly becomes more negative as the recording electrode is moved from outside to inside, so excitable cells are said to 0 Frog have a negative resting potential. Again by conven- Node tion any potential change in the positive direction ,-25 22°C from rest is called a depolarization, whereas a change in the negative direction is called a hyperpolariza- tion. Intracellular records from several types of nerve -I75 d ‘L fiber and a motoneuron are shown in Figure 1. In 0 05 each example in Figure 1 excitation is initiated by a L..& m sec depolarizing electric shock, and the nerve cell re- sponds with a depolarizing electric response, the ac- tion potential, also called a spike or impulse. Action potentials are generally similar in all cells but differ in details of shape and time course from one cell type to another. The simple observation that both the stimulus and response are electric is intimately tied in with the mechanisrn of propagation of activity or conduction of action potentials. The response is said to be regenerative because electric currents generated by the action potential in one part of an axon are sufficient to excite the next part of the axon, and so 024 msec forth. Thus the impulse travels as a wave down the +so - length of an axon at fairly steady speed and ampli- tude. This voltage pulse is the unit of information in D nerve fibers and, as will be shown, is generated and >o n shaped by ionic permeability changes in each patch of E axon membrane. Sodium and potassium ions are by far the most important ions. Squid Axon 16°C DEVELOPMENT OF MEMBRANE THEORY - h Before Intracellular Recording 0 2 4 6 8 msec ORIGINS. The membrane theory dates from the begin- FIG. 1. Intracellularly recorded resting and action potentials ning of this century arid has roots in previous centu- from several nerve cells. A; single node of Ranvier of rat myelin- ries. At the end of the eighteenth century Galvani ated nerve fiber at 37°C. Brief stimulus applied at same node. (W. concluded that nerves and muscles use a flow of Nonner, M. Hordtkova, and R. Stampfli, unpublished data.) B: “animal electricity” to communicate with the brain. same type of recording from frog myelinated fiber as in A, but at He supposed that the body stores positive and nega- 22°C. [From Dodge (56).] C; cat lumbar spinal motoneuron at 3TC, excited antidromically by stimulation of motor axon. (W. E. tive electricity separated by insulators. In the nine- Crill, unpublished data.) I): propagating action potential in squid teenth century the electric currents of nerve and giant axon at 16°C. Stimulus applied about 2 cm from recording muscle were found to produce brief, externally nega- site. [From Baker et al. (23.) tive voltage pulses traveling at high velocity along nerves and muscles. Nerves were correctly likened to permeable to potassium ions at rest. Bernstein knew electrical cables with a surface insulation- the core that K+ is at higher concentration inside cells than conductor theory. There were arguments whether the outside. Thus K+ would tend to diffuse out, removing electricity is there all t.he time or is generated only at positive charge from the cell interior and setting up a the time of the impulse. Near the end of the century negative internal potential. The potential continues there was an essential advance in physical chemis- to develop until it is so large as to oppose the further try. Arrhenius (17) showed that salts dissociate into net emux of K+ (i.e., until diffusion forces and elec- ions. Then Nernst (180, 181) and Planck (191, 192) tric forces exactly cancel). For a membrane exclu- gave theories for equilibrium and diffusion potentials sively permeable to K+, the potential can be calcu- in ionic solutions, and Nernst and W. V. Ostwald lated from the Nernst equation for equilibrium poten- remarked that biological potentials might also be tials explainable by the same theories. The membrane theory is usually attributed to the physiologist Bernstein (26, 27) who suggested in 1902 that nerve and muscle cell membranes are selectively CHAF’TER 4: IONIC BASIS OF RESTING AND ACTION POTENTIALS 101 where [KJ, and [K], are the outside and inside potas- STRENGTH - DURATION sium ion concentrations, z the valence (+11, R the gas Toad sciatic nerve 10.2”C constant, T the absolute temperature, and F the Faraday. At 20°C the value of RTIF is 25.3 mV (see Table 4 in section EQUATIONS OF IONIC HYPOTHESIS). E is called the potassium equilibrium potential. For no concentration difference, E, is 0 mV, and for a 10- fold higher internal K+ concentration than outside, E, is -58.2 mV. Bernstein’s theory was suggested by I __---- the depolarizing effect of salts of potassium applied to I\-- f----- i- the surface of nerves. Bernstein (26) further sug- Rheobase gested that the propagated impulse involves “an in- 41 I f+ crease of membrane permeability for the retained ion 0 5 10 43 due to a chemical change of the plasma [membrane].” Shock duration (msec) In his view this wave of permeability change over- REFRACTORY PER I OD comes the potassium potential by allowing all ions to B, diffuse across the membrane simultaneously. In the 4-.f Frog sciatic nerve 148OC 2 (1 English-language literature the permeability in- t crease was dubbed a membrane “breakdown.” Unfor- ? 3- tunately intracellular recording was unknown in 1902, so most quantitative features of Bernstein’s proposal were temporarily untestable. STIMULATION. Bernstein’s ideas were generally ac- cepted for 40 years with little proof, as axonologists worked on questions approachable with extracellular recording. When a nerve is artificially stimulated by an externally applied electric shock, the impulse nor- I I 1 I mally arises at the electrode producing depolariza- 0 10 20 30 tion, the cathode or negative (external) electrode. Interval between shocks (msec) Large shocks stimulate more of the fibers in a nerve FIG. 2. Strength-duration curve and refractory period in large myelinated fibers of cooled amphibian sciatic nerve. Threshold than small shocks, and none of the fibers is excited if shock measured as the smallest amplitude shock to the nerve that the shock is too weak. Each individual fiber either makes a just-detectable twitch in an attached whole muscle. A: does or does not give a propagated response, depend- threshold shock amplitude vs. shock duration for a single rectan- ing on if the shock is greater or less than a critical gular shock. [Data from Lucas (163.1 B: threshold shock ampli- threshold value for that fiber.
Load more

Recommended publications
  • Thenerveimpulse05.Pdf
    The nerve impulse. INTRODUCTION Axons are responsible for the transmission of information between different points of the nervous system and their function is analogous to the wires that connect different points in an electric circuit. However, this analogy cannot be pushed very far. In an electrical circuit the wire maintains both ends at the same electrical potential when it is a perfect conductor or it allows the passage of an electron current when it has electrical resistance. As we will see in these lectures, the axon, as it is part of a cell, separates its internal medium from the external medium with the plasma membrane and the signal conducted along the axon is a transient potential difference1 that appears across this membrane. This potential difference, or membrane potential, is the result of ionic gradients due to ionic concentration differences across the membrane and it is modified by ionic flow that produces ionic currents perpendicular to the membrane. These ionic currents give rise in turn to longitudinal currents closing local ionic current circuits that allow the regeneration of the membrane potential changes in a different region of the axon. This process is a true propagation instead of the conduction phenomenon occurring in wires. To understand this propagation we will study the electrical properties of axons, which include a description of the electrical properties of the membrane and how this membrane works in the cylindrical geometry of the axon. Much of our understanding of the ionic mechanisms responsible for the initiation and propagation of the action potential (AP) comes from studies on the squid giant axon by A.
    [Show full text]
  • Spatial Extent of Neurons: Dendrites and Axons
    Spatial extent of neurons: dendrites and axons Morphological diversity of neurons Cortical pyramidal cell Purkinje cell Retinal ganglion cells Motoneurons Dendrites: spiny vs non-spiny Recording and simulating dendrites Axons - myelinated vs unmyelinated Axons - myelinated vs unmyelinated • Myelinated axons: – Long-range axonal projections (motoneurons, long-range cortico-cortical connections in white matter, etc) – Saltatory conduction; – Fast propagation (10s of m/s) • Unmyelinated axons: – Most local axonal projections – Continuous conduction – Slower propagation (a few m/s) Recording from axons Recording from axons Recording from axons - where is the spike generated? Modeling neuronal processes as electrical cables • Axial current flowing along a neuronal cable due to voltage gradient: V (x + ∆x; t) − V (x; t) = −Ilong(x; t)RL ∆x = −I (x; t) r long πa2 L where – RL: total resistance of a cable of length ∆x and radius a; – rL: specific intracellular resistivity • ∆x ! 0: πa2 @V Ilong(x; t) = − (x; t) rL @x The cable equation • Current balance in a cylinder of width ∆x and radius a • Axial currents leaving/flowing into the cylinder πa2 @V @V Ilong(x + ∆x; t) − Ilong(x; t) = − (x + ∆x; t) − (x; t) rL @x @x • Ionic current(s) flowing into/out of the cell 2πa∆xIion(x; t) • Capacitive current @V I (x; t) = 2πa∆xc cap M @t • Kirschoff law Ilong(x + ∆x; t) − Ilong(x; t) + 2πa∆xIion(x; t) + Icap(x; t) = 0 • In the ∆x ! 0 limit: @V a @2V cM = 2 − Iion @t 2rL @x Compartmental appoach Compartmental approach Modeling passive dendrites: Cable equation
    [Show full text]
  • Structure and Function Relationship in Nerve Cells & Membrane Potential
    Structure and Function Relationship in Nerve Cells & Membrane Potential Asist. Prof. Aslı AYKAÇ NEU Faculty of Medicine Biophysics Nervous System Cells • Glia – Not specialized for information transfer – Support neurons • Neurons (Nerve Cells) – Receive, process, and transmit information Neurons • Neuron Doctrine – The neuron is the functional unit of the nervous system • Specialized cell type – have very diverse in structure and function Neuron: Structure/Function • designed to receive, process, and transmit information – Dendrites: receive information from other neurons – Soma: “cell body,” contains necessary cellular machinery, signals integrated prior to axon hillock – Axon: transmits information to other cells (neurons, muscles, glands) • Information travels in one direction – Dendrite → soma → axon How do neurons work? • Function – Receive, process, and transmit information – Conduct unidirectional information transfer • Signals – Chemical – Electrical Membrane Potential Because of motion of positive and negative ions in the body, electric current generated by living tissues. What are these electrical signals? • receptor potentials • synaptic potentials • action potentials Why are these electrical signals important? These signals are all produced by temporary changes in the current flow into and out of cell that drives the electrical potential across the cell membrane away from its resting value. The resting membrane potential The electrical membrane potential across the membrane in the absence of signaling activity. Two type of ions channels in the membrane – Non gated channels: always open, important in maintaining the resting membrane potential – Gated channels: open/close (when the membrane is at rest, most gated channels are closed) Learning Objectives • How transient electrical signals are generated • Discuss how the nongated ion channels establish the resting potential.
    [Show full text]
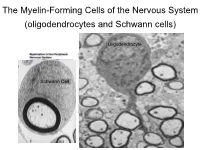
  • The Myelin-Forming Cells of the Nervous System (Oligodendrocytes and Schwann Cells)
    The Myelin-Forming Cells of the Nervous System (oligodendrocytes and Schwann cells) Oligodendrocyte Schwann Cell Oligodendrocyte function Saltatory (jumping) nerve conduction Oligodendroglia PMD PMD Saltatory (jumping) nerve conduction Investigating the Myelinogenic Potential of Individual Oligodendrocytes In Vivo Sparse Labeling of Oligodendrocytes CNPase-GFP Variegated expression under the MBP-enhancer Cerebral Cortex Corpus Callosum Cerebral Cortex Corpus Callosum Cerebral Cortex Caudate Putamen Corpus Callosum Cerebral Cortex Caudate Putamen Corpus Callosum Corpus Callosum Cerebral Cortex Caudate Putamen Corpus Callosum Ant Commissure Corpus Callosum Cerebral Cortex Caudate Putamen Piriform Cortex Corpus Callosum Ant Commissure Characterization of Oligodendrocyte Morphology Cerebral Cortex Corpus Callosum Caudate Putamen Cerebellum Brain Stem Spinal Cord Oligodendrocytes in disease: Cerebral Palsy ! CP major cause of chronic neurological morbidity and mortality in children ! CP incidence now about 3/1000 live births compared to 1/1000 in 1980 when we started intervening for ELBW ! Of all ELBW {gestation 6 mo, Wt. 0.5kg} , 10-15% develop CP ! Prematurely born children prone to white matter injury {WMI}, principle reason for the increase in incidence of CP ! ! 12 Cerebral Palsy Spectrum of white matter injury ! ! Macro Cystic Micro Cystic Gliotic Khwaja and Volpe 2009 13 Rationale for Repair/Remyelination in Multiple Sclerosis Oligodendrocyte specification oligodendrocytes specified from the pMN after MNs - a ventral source of oligodendrocytes
    [Show full text]
  • Gathering at the Nodes
    RESEARCH HIGHLIGHTS GLIA Gathering at the nodes Saltatory conduction — the process by which that are found at the nodes of Ranvier, where action potentials propagate along myelinated they interact with Na+ channels. When the nerves — depends on the fact that voltage- authors either disrupted the localization of gated Na+ channels form clusters at the nodes gliomedin by using a soluble fusion protein of Ranvier, between sections of the myelin that contained the extracellular domain of sheath. New findings from Eshed et al. show neurofascin, or used RNA interference to that Schwann cells produce a protein called suppress the expression of gliomedin, the gliomedin, and that this is responsible for characteristic clustering of Na+ channels at the clustering of these channels. the nodes of Ranvier did not occur. The formation of the nodes of Ranvier is Aggregation of the domain of gliomedin specified by the myelinating cells, not the that binds neurofascin and NrCAM on the axons, and an important component of this surface of purified neurons also caused process in the peripheral nervous system the clustering of neurofascin, Na+ channels is the extension of microvilli by Schwann and other nodal proteins. These findings cells. These microvilli contact the axons at support a model in which gliomedin on the nodes, and it is here that the Schwann References and links Schwann cell microvilli binds to neurofascin ORIGINAL RESEARCH PAPER Eshed, Y. et al. Gliomedin cells express the newly discovered protein and NrCAM on axons, causing them to mediates Schwann cell–axon interaction and the molecular gliomedin. cluster at the nodes of Ranvier, and leading assembly of the nodes of Ranvier.
    [Show full text]
  • New Plasmon-Polariton Model of the Saltatory Conduction
    bioRxiv preprint doi: https://doi.org/10.1101/2020.01.17.910596; this version posted January 20, 2020. The copyright holder for this preprint (which was not certified by peer review) is the author/funder. All rights reserved. No reuse allowed without permission. Manuscript submitted to BiophysicalJournal Article New plasmon-polariton model of the saltatory conduction W. A. Jacak1,* ABSTRACT We propose a new model of the saltatory conduction in myelinated axons. This conduction of the action potential in myelinated axons does not agree with the conventional cable theory, though the latter has satisfactorily explained the electro- signaling in dendrites and in unmyelinated axons. By the development of the wave-type concept of ionic plasmon-polariton kinetics in axon cytosol we have achieved an agreement of the model with observed properties of the saltatory conduction. Some resulting consequences of the different electricity model in the white and the gray matter for nervous system organization have been also outlined. SIGNIFICANCE Most of axons in peripheral nervous system and in white matter of brain and spinal cord are myelinated with the action potential kinetics speed two orders greater than in dendrites and in unmyelinated axons. A decrease of the saltatory conduction velocity by only 10% ceases body functioning. Conventional cable theory, useful for dendrites and unmyelinated axon, does not explain the saltatory conduction (discrepancy between the speed assessed and the observed one is of one order of the magnitude). We propose a new nonlocal collective mechanism of ion density oscillations synchronized in the chain of myelinated segments of plasmon-polariton type, which is consistent with observations.
    [Show full text]
  • The Calyx of Held
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by RERO DOC Digital Library Cell Tissue Res (2006) 326:311–337 DOI 10.1007/s00441-006-0272-7 REVIEW The calyx of Held Ralf Schneggenburger & Ian D. Forsythe Received: 6 April 2006 /Accepted: 7 June 2006 / Published online: 8 August 2006 # Springer-Verlag 2006 Abstract The calyx of Held is a large glutamatergic A short history of the calyx of Held synapse in the mammalian auditory brainstem. By using brain slice preparations, direct patch-clamp recordings can The size of a synapse is a significant technical constraint for be made from the nerve terminal and its postsynaptic target electrophysiological recording. The large dimensions of (principal neurons of the medial nucleus of the trapezoid some invertebrate synapses have been exploited to provide body). Over the last decade, this preparation has been considerable insight into presynaptic function (Llinas et al. increasingly employed to investigate basic presynaptic 1972; Augustine et al. 1985; Young and Keynes 2005). mechanisms of transmission in the central nervous system. However, the progress of similar studies in vertebrates was We review here the background to this preparation and long hampered by the technical difficulty of presynaptic summarise key findings concerning voltage-gated ion recording from small nerve terminals. Over the last 50 years, channels of the nerve terminal and the ionic mechanisms a range of preparations have contributed to our understand- involved in exocytosis and modulation of transmitter ing of presynaptic mechanisms, from the neuromuscular release. The accessibility of this giant terminal has also junction (Katz 1969) to chromaffin cells (Neher and Marty permitted Ca2+-imaging and -uncaging studies combined 1982), chick ciliary ganglion (Martin and Pilar 1963; with electrophysiological recording and capacitance mea- Stanley and Goping 1991), neurohypophysial nerve termi- surements of exocytosis.
    [Show full text]
  • The Nervous System Action Potentials
    The Nervous System Action potentials Jennifer Carbrey Ph.D. Department of Cell Biology Nervous System Cell types neurons glial cells Methods of communication in nervous system – action potentials How the nervous system is organized central vs. peripheral Voltage Gated Na+ & K+ Channels image by Rick Melges, Duke University Depolarization of the membrane is the stimulus which leads to both channels opening. To reset the Na+ channel from inactive to closed need to repolarize the membrane. Refractory period is when Na+ channels are inactivated. Action Potentials stage are rapid, “all or none” and do not decay over 1 2 3 4 5 distances top image by image by Chris73 (modified), http://commons.wikimedia.org/wiki/File:Action_potential_%28no_labels%29.svg, Creative Commons Attribution-Share Alike 3.0 Unported license bottom image by Rick Melges, Duke University Unidirectional Propagation of AP image by Rick Melges, Duke University Action potentials move one-way along the axon because of the absolute refractory period of the voltage gated Na+ channel. Integration of Signals Input: Dendrites: ligand gated ion channels, some voltage gated channels; graded potentials Cell body (Soma): ligand gated ion channels; graded potentials Output: Axon: voltage gated ion channels, action potentials Axon initial segment: highest density of voltage gated ion channels & lowest threshold for initiating an action potential, “integrative zone” Axon Initial Segment image by Rick Melges, Duke University Integration of signals at initial segment Saltatory Conduction Node of Ranvier Na+ action potential Large diameter, myelinated axons transmit action potentials very rapidly. Voltage gated channels are concentrated at the nodes. Inactivation of voltage gated Na+ channels insures uni-directional propagation along the axon.
    [Show full text]
  • Neuronal Signaling Neuroscience Fundamentals > the Nerve Cell > the Nerve Cell
    Neuronal Signaling Neuroscience Fundamentals > The Nerve Cell > The Nerve Cell NEURONAL SIGNALING SUMMARY ACTION POTENTIALS See: Action Potentials Key Features • All-or-nothing events • Self-propagating • Conduction speed determined by axon diameter (thicker means faster) and amount of myelination (more myelin means faster transmission). CHEMICAL SYNAPSE Steps of Chemical Synapsis 1) The action potential travels down axon of presynaptic neuron. 2) Vesicle fuses with plasma membrane and releases neurotransmitter into the synaptic cleft. 3) Neurotransmitters bind to ligand-gated ion channels, opening them. 4) Ions entering through the open channels cause a depolarization of the membrane, opening voltage-gated ion channels. 5) Ions pass through these voltage-gated ion channels, causing further depolarization of the membrane. 6) This depolarization (action potential) travels along the membrane as more voltage-gated ion channels are opened. ELECTRICAL SYNAPSE • Cytoplasms of adjacent neurons are connected, allowing ions (and action potentials) to travel directly to the next cell. NEURONAL CODING OF STIMULUS STRENGTH Action Potential Frequency • Stimulus strength is based on frequency of action potentials. Action Potential Strength • Strong stimuli can produce another action potential during the relative refractory period. 1 / 7 ABSOLUTE REFRACTORY PERIOD No further action potentials • Voltage-gated sodium channels are open or inactivated so another stimulus, no matter its strength, CANNOT elicit another action potential. RELATIVE REFRACTORY
    [Show full text]
  • Computation of Impulse Initiation and Saltatory Conduction in a Myelinated Nerve Fiber
    View metadata, citation and similar papers at core.ac.uk brought to you by CORE provided by Elsevier - Publisher Connector COMPUTATION OF IMPULSE INITIATION AND SALTATORY CONDUCTION IN A MYELINATED NERVE FIBER RICHARD FITZHUGH From the National Institutes of Health, Bethesda ABSTRACT A mathematical model of the electrical properties of a myelinated nerve fiber is given, consisting of the Hodgkin-Huxley ordinary differential equations to represent the membrane at the nodes of Ranvier, and a partial differential cable equation to represent the internodes. Digital computer solutions of these equations show an impulse arising at a stimulating electrode and being propagated away, approaching a constant velocity. Action potential curves plotted against distance show discontinuities in slope, proportional to the nodal action currents, at the nodes. Action potential curves plotted against time, at the nodes and in the internodes, show a marked difference in steepness of the rising phase, but little difference in peak height. These results and computed action current curves agree fairly accurately with published experimental data from frog and toad fibers. INTRODUCTION Hodgkin and Huxley's set of ordinary differential equations for the squid giant nerve fiber membrane has previously been solved for the case of a space clamp, in which the potential, current, and other variables of state of the membrane vary with time but not with distance along the fiber (Hodgkin and Huxley, 1952; Cole, Antosiewicz, and Rabinowitz, 1955; FitzHugh and Antosiewicz, 1959; FitzHugh, 1960; George, 1960; FitzHugh, 1961). Cases in which these variables vary with distance as well as with time are described by the partial differential equation of Hodgkin and Huxley, which is a cable equation with a distributed Hodgkin-Huxley (HH) membrane instead of the usual passive resistive layer.
    [Show full text]
  • Tutorial 8: Saltatory Conduction Figure 8A
    Saltatory Conduction - Introduction 06/11/02 15:20 Tutorial 8: Saltatory Conduction Show Labels | Remove Labels Figure 8a: Saltatory Conduction Intro | Figure 8a | Figure 8b Part 1: Image-Mapped Tutorial Part 2: Matching Self-Test Part 3: Multiple-Choice Self-Test Return to main tutorial page Tutorial 8 discusses the anatomy and physiology that increase the rate at which an action potential is conducted down the axon. Figure 8a focuses on the relevant anatomy, while Figure 8b describes the physiological mechanism. Saltatory conduction (from the Latin word "to dance"), as this enhanced conduction is called, depends on the myelin sheaths introduced in Tutorial 2. Saltatory conduction provides two advantages over conduction that occurs along an axon without myelin sheaths. First, it saves energy by decreasing the use of sodium-potassium pumps in the axonal membrane. Secondly, the increased speed afforded by this mode of conduction allows the organism to react and think faster. Advanced Multiple sclerosis is a common neurological disorder characterized by patchy demyelination of axons in the central nervous system (Giovannoni & Miller, 1999). The symptoms of this disorder reflect the disruption of normal function of the neurons affected by demyelination. These symptoms commonly remit for a period of time after their onset. The exacerbation and reduction of symptoms follow a cycle of demyelination and remyelination. It was not known until very recently, what mechanism was responsible for the remyelination process. Until recently a precursor cell for the oligodendrocyte and Schwann cell had been identified in rodents, http://psych.athabascau.ca/html/Psych402/Biotutorials/8/intro.shtml?print Page 1 sur 3 Saltatory Conduction - Introduction 06/11/02 15:20 but not humans (Engel & Wolswijk G, 1996).
    [Show full text]
  • Arxiv:1708.00534V1 [Q-Bio.NC] 1 Aug 2017 Myelin and Saltatory Conduction
    Myelin and saltatory conduction Maurizio De Pitt`a The University of Chicago, USA EPI BEAGLE, INRIA Rhˆone-Alpes, France August 3, 2017 (Submitted as contributed section to the chapter on “Neurophysiology” of the book “Da˜no cerebral” (Brain damage), JC Arango-Asprilla & L Olabarrieta-Landa eds., Manual Moderno Editions.) arXiv:1708.00534v1 [q-bio.NC] 1 Aug 2017 1 Myelin allows fast and reliable conduction of nerve pulses Myelin is a fatty substance that ensheathes the axon of some nerve cells, forming an electrically insulating layer. It is considered a defining characteristic of jawed vertebrates and is essential for the proper functioning of the nervous system of these latter. Myelin is made by different cell types, and varies in chemical composition and configuration, but performs the same insulating function. Myelinated axons look like strings of sausages under a microscope, and because of their white appearance they are integral components of the “white matter” of the brain. The myelin sausages ensue from wrapping of axons by myelin in multiple, concentric layers and are separated from each others by small unmyelinated axonal segments known as nodes of Ranvier. Typically the length of a node is very small (0.1%) compared to the length of the myelinated segment. Single myelinated fibers range in diameter from 0.2 to 20 µm on average, while unmyelinated fibers range between 0.1 and 1 µm [1]. Peripheral axons are myelinated only if their diameter is larger than about 1 µm, and the axonal caliber maintains a rather constant ratio to the myelin sheath thickness [2]. A normal myelin ensheathing of a mature peripheral nerve is usually 100 times as long as the diameter of the corresponding axon [3].
    [Show full text]